Sprawdź się

1
Pokaż ćwiczenia:
RVfAVGbKBPpcc1
Ćwiczenie 1
Wskaż wszystkie zdania prawdziwe Możliwe odpowiedzi: 1. Na danym okręgu można opisać nieskończenie wiele trójkątów., 2. W dany trójkąt można wpisać nieskończenie wiele okręgów., 3. Jeżeli w trójkąt wpisany jest okrąg o promieniu r, to trójkąt podobny do danego trójkąta w skali 3 jest trójkątem opisanym na okręgu o promieniu 3r., 4. Jeżeli trójkąt jest opisany na okręgu to punkty styczności okręgu z tym trójkątem tworzą trójkąt rozwartokątny., 5. Jeżeli trójkąt jest opisany na okręgu to kąty środkowe oparte na cięciwach łączących punkty styczności okręgu z tym trójkątem mają miarę mniejszą od 180°.
1
Ćwiczenie 2

Na rysunku przedstawiony jest okrąg i trójkąt ABC opisany na tym okręgu. Jeżeli dwa kąty trójkąta ABC mają miary 90° i 60° oraz przeciwprostokątna AB ma długość 20, to:

R3UFVfjbRL4Ua
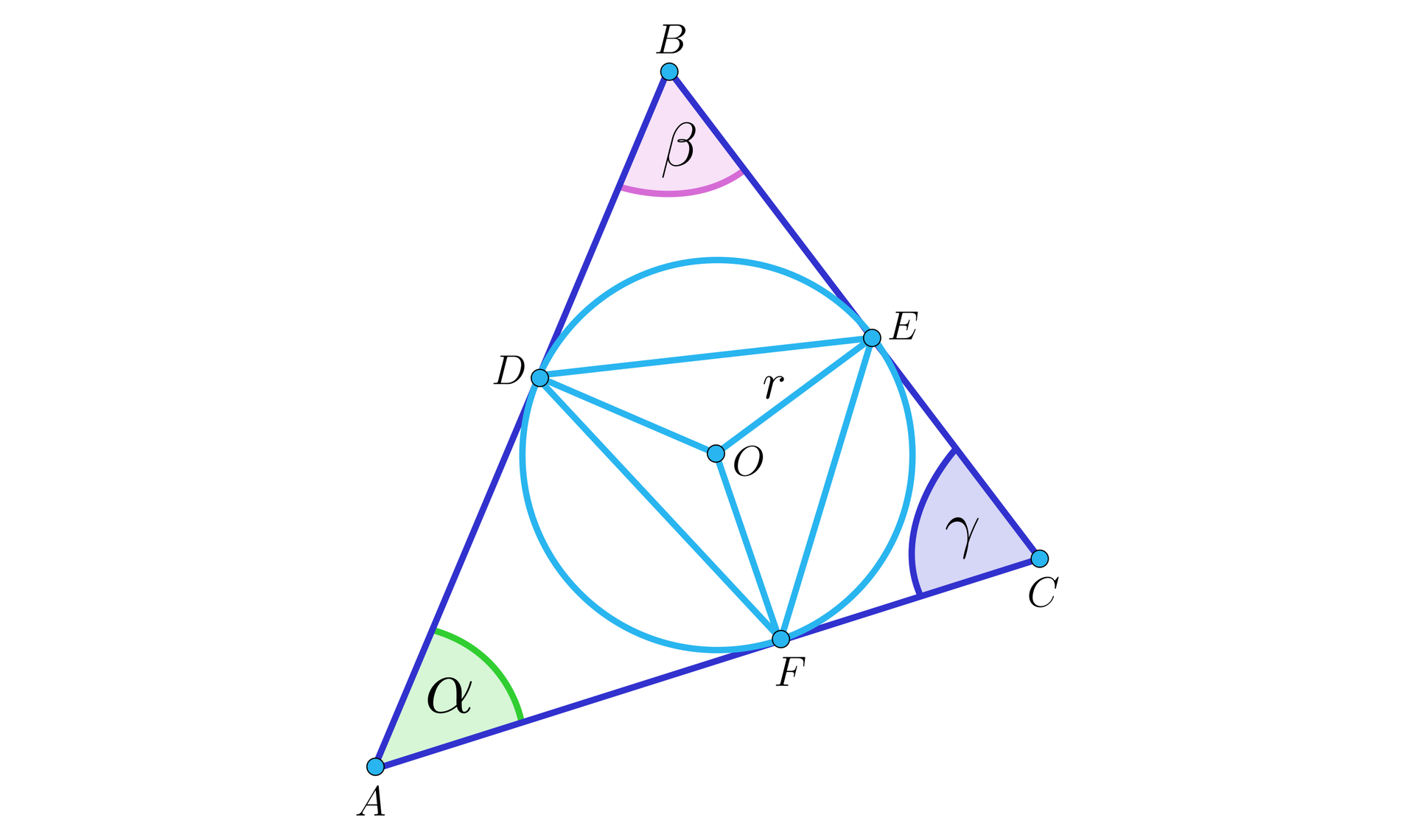
Ilustracja przedstawia trójkąt ABC o kątach ABC równym beta oznaczonym na różowo , BCA równym gamma oznaczonym na niebiesko i CAB równym alfa oznaczonym na zielono. Wpisany jest w niego okrąg o środku O który jest styczny z trójkątem ABC w punkcie D na boku AB , punkcie E na boku BC oraz punkcie F na boku AC. W okręgu zaznaczono również promienie o długości r które dochodzą do punków styku. Punkty styku są jednoczenie wierzchołkami trójkąta DEF wpisanego w okrąg.
R4HuKtMz0B2Hl
Łączenie par. . 90°. Możliwe odpowiedzi: Jeden z kątów trójkąta DEF ma miarę:, Jeżeli przeciwprostokątna AB ma długość 20 to jedna z przyprostokątnych ma długość:. 120°. Możliwe odpowiedzi: Jeden z kątów trójkąta DEF ma miarę:, Jeżeli przeciwprostokątna AB ma długość 20 to jedna z przyprostokątnych ma długość:. 60°. Możliwe odpowiedzi: Jeden z kątów trójkąta DEF ma miarę:, Jeżeli przeciwprostokątna AB ma długość 20 to jedna z przyprostokątnych ma długość:. 240°. Możliwe odpowiedzi: Jeden z kątów trójkąta DEF ma miarę:, Jeżeli przeciwprostokątna AB ma długość 20 to jedna z przyprostokątnych ma długość:. 150°. Możliwe odpowiedzi: Jeden z kątów trójkąta DEF ma miarę:, Jeżeli przeciwprostokątna AB ma długość 20 to jedna z przyprostokątnych ma długość:
RedipfSBOFh0R2
Ćwiczenie 3
Wymyśl pytanie na kartkówkę związane z tematem materiału.
2
Ćwiczenie 4

Jakie warunki powinny spełniać kąty środkowe oparte na cięciwach DE, EF, FD, żeby trójkąt ABC opisany na okręgu ośrodku O i promieniu r był prostokątny?

R1RMsyJh9GWlY
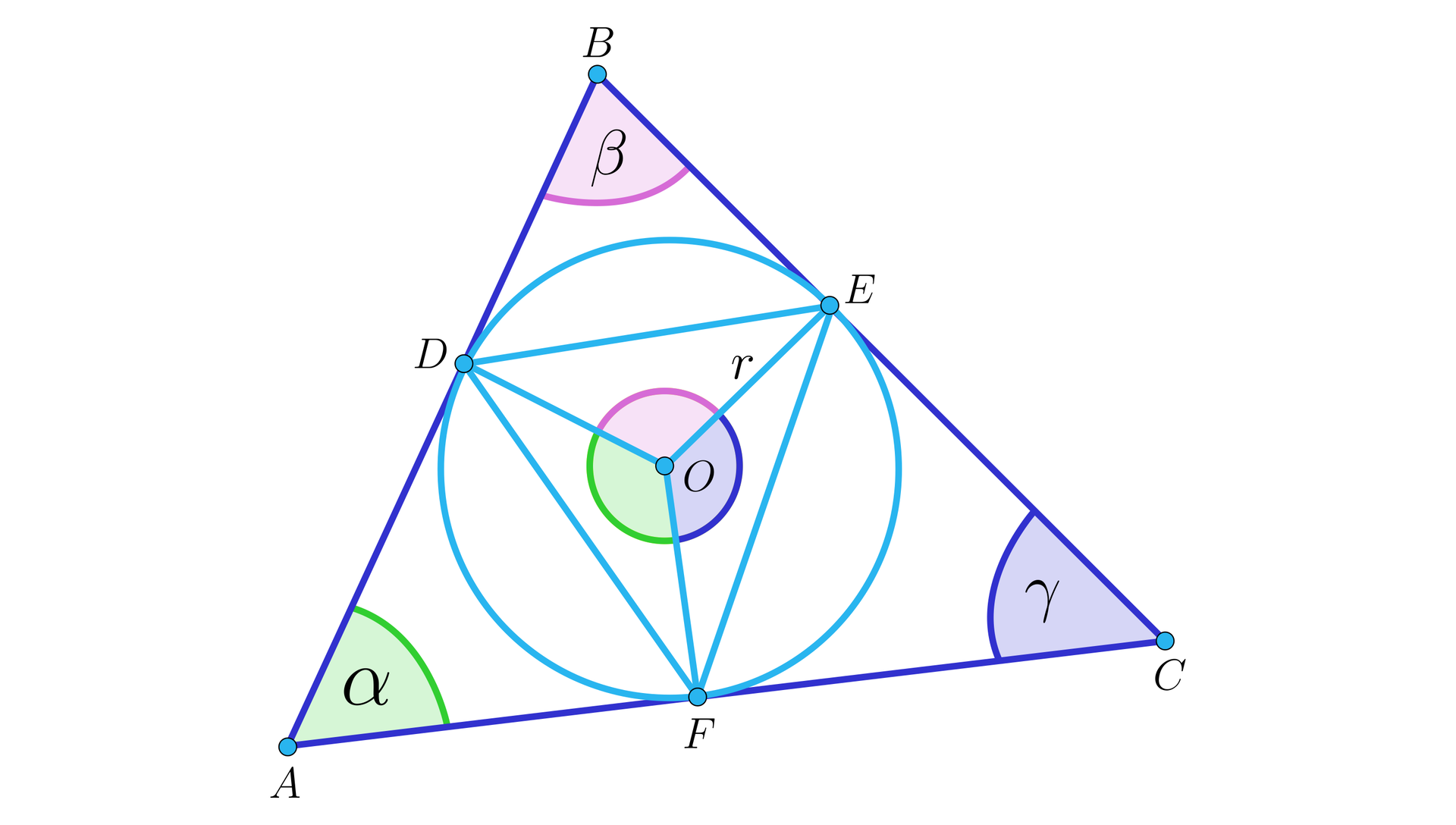
Ilustracja przedstawia trójkąt ABC, gdzie kąt ABC podpisano literą beta i oznaczono na różowo , kąt BCA podpisano literą gamma i oznaczono na niebiesko i kąt CAB podpisano literą alfa i oznaczono na zielono. W trójkąt ten wpisany jest okrąg o środku O który jest styczny z trójkątem ABC w punkcie D na boku AB , punkcie E na boku BC oraz punkcie F na boku AC. W okręgu zaznaczono również promienie o długości r które dochodzą do punków styku. Punkty styku są jednoczenie wierzchołkami trójkąta DEF wpisanego w okrąg. Kąt DOF oznaczony jest na zielono , DOE na różowo oraz FOE na niebiesko.
2
Ćwiczenie 5

Na okręgu o środku O i promieniu r opisano trójkąt równoramienny taki, że odległość środka okręgu od wierzchołka przy ramionach tego trójkąta jest równa średnicy okręgu. Pokaż, że trójkąt ten jest równoboczny.

RwYNQCZOT6GYf
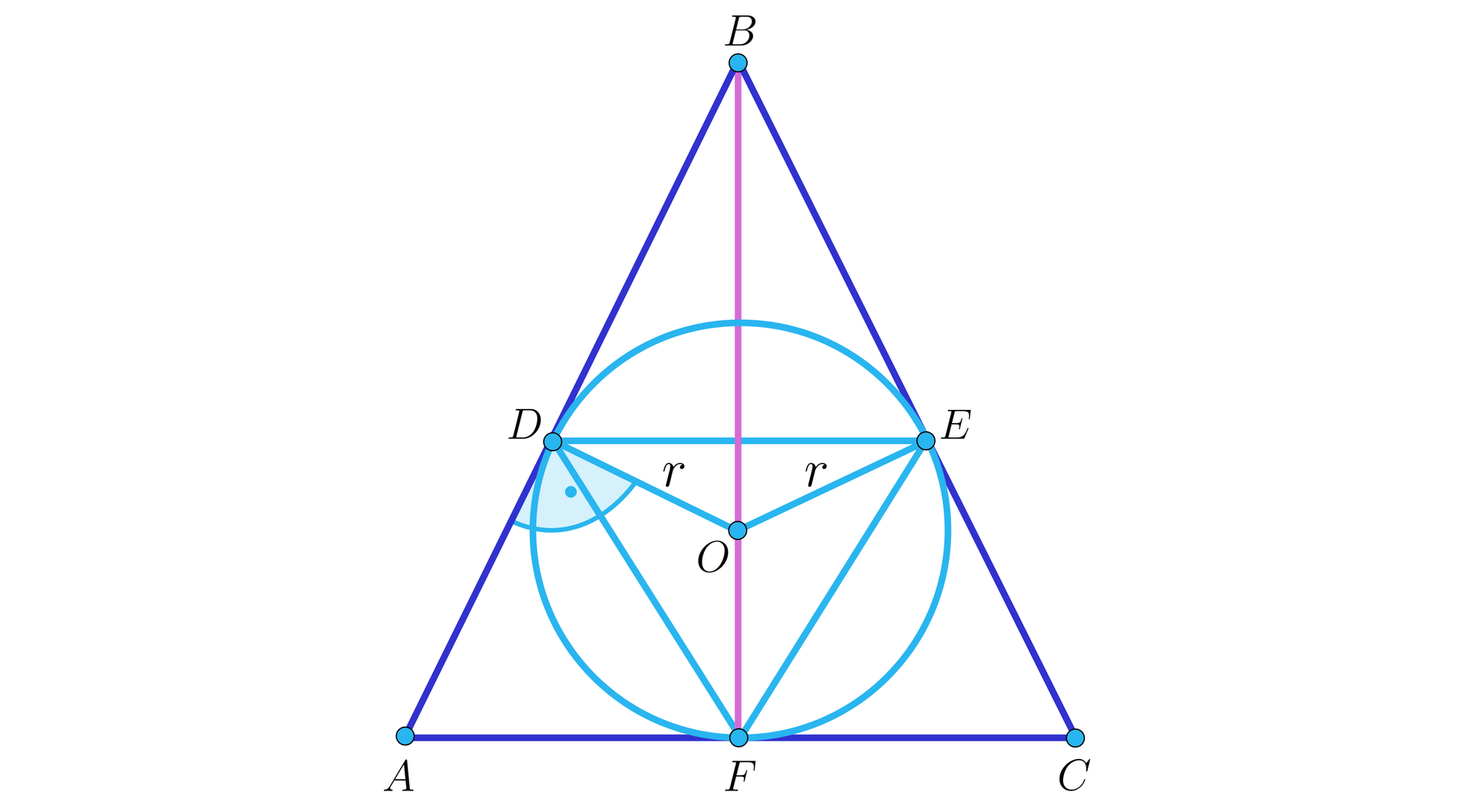
Grafika przedstawia trójkąt ABC w który wpisany jest okrąg o środku O. Okrąg styka się z trójkątem w punkcie D na boku AB , tworząc odcinki AD i DB , w punkcie E na boku CB tworząc odcinki CE i EB oraz w punkcie F na boku AC tworząc odcinki AF i FC . W okręgu zaznaczono również promienie o długości r które dochodzą do punków styku D i E oraz wysokość trójkąta opuszczoną z wierzchołka B do punktu F. Oznaczono kąt prosty ADO. Punkty styku są jednoczenie wierzchołkami trójkąta DEF wpisanego w okrąg.
2
Ćwiczenie 6

Na okręgu o promieniu 10 opisano trójkąt równoramienny o podstawie 30. Następnie poprowadzono odcinek DE styczny do okręgu i równoległy do podstawy trójkąta. W powstały trójkąt CDE wpisano okrąg. Wyznacz promień tego okręgu.

R8sy8xpDGbK6F
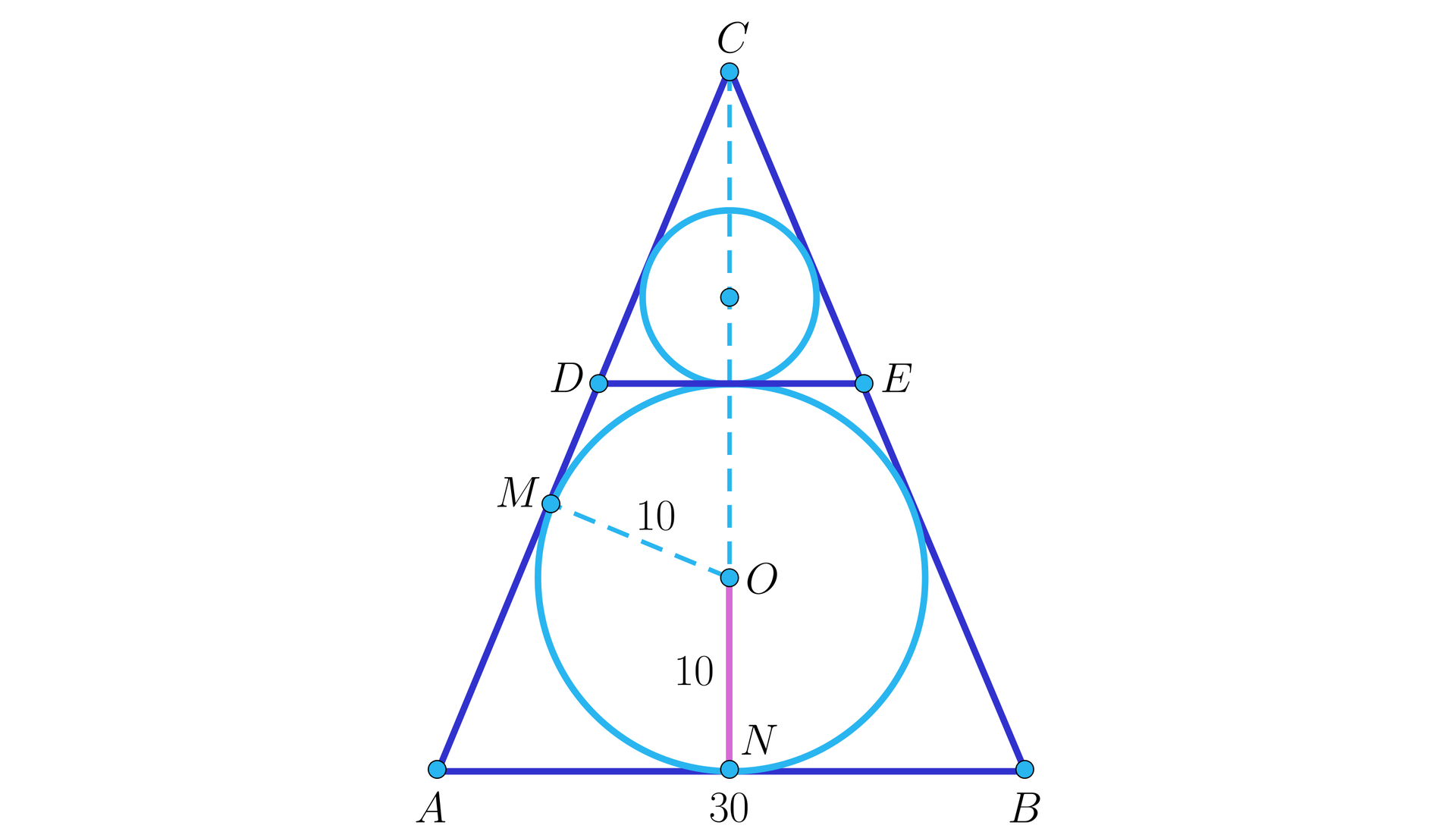
Na ilustracji przedstawiony jest trójkąt ABC z podstawą AB o długości 30 . Na boku AC znajduje się punkt D dzielący bok na odcinki AD i DC , na boku CB jest punkt E dzielący bok na odcinki CE i EB a na boku AB punkt N dzielący bok na odcinki AN i NB . Linia DE równoległa do podstawy trójkąta AB , dzieli trójkąt ABC na trójkąt CED oraz trapez ABED . W trójkąt CED i trapez wpisane są okręgi , w trapezie jest to okrąg o środku O. Odcinek ON będący promieniem okręgu ma długość 10 . Na odcinku AD znajduje się punkt M do którego również dochodzi promień oznaczony linią przerywaną . Również linią przerywaną oznaczony jest odcinek OC przechodzący przez środek okręgu wpisanego w trójkąt DCE.
3
Ćwiczenie 7

Na rysunku trójkąt ABC jest wpisany w okrąg zielony. Na tym okręgu opisano trójkąt DEF tak, żeby punkty A, B, C były punktami styczności. Następnie opisano okrąg niebieski na trójkącie DEF i opisano trójkąt GHI na tym okręgu tak, żeby punkty D, E, F były punktami styczności. Wyznacz kąty trójkątów DEF i ABC, jeżeli trójkąt GHI ma kąty 120°, 40°, 20°.

R1RHsoePaMr32
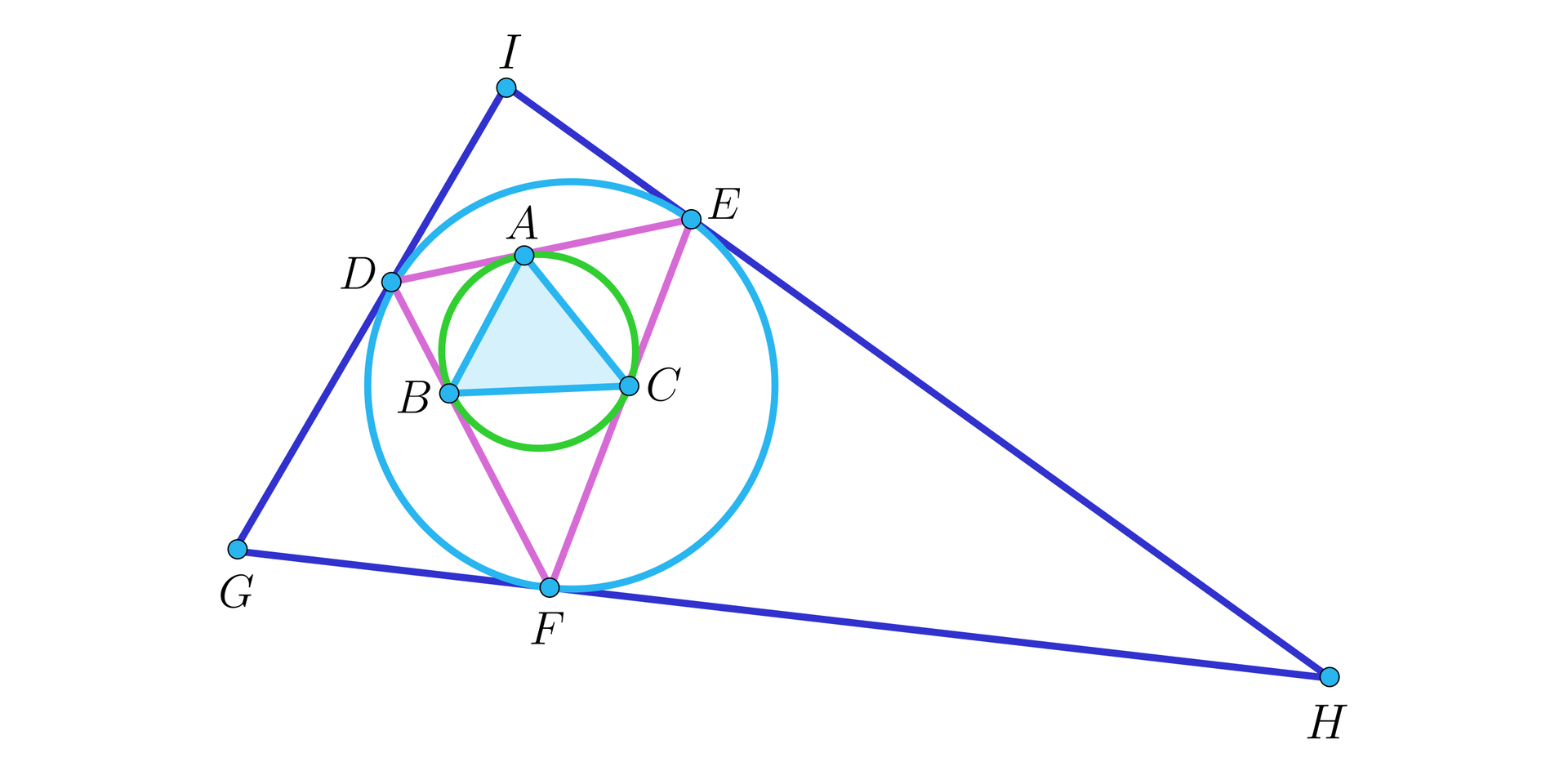
Grafika przedstawia niebieski trójkąt ABC wpisany w okrąg o kolorze zielonym . Przez punkty A B i C przechodzą styczne które tworzą opisany na zielonym okręgu trójkąt o wierzchołkach DEF . Trójkąt DEF jest jednocześnie wpisany w niebieski okrąg. Na niebieskim okręgu opisano ciemnoniebieski trójkąt o wierzchołkach GHI który jest styczny do niebieskiego okręgu w punktach D, E i F.
3
Ćwiczenie 8

Na rysunku trójkąt ABC jest wpisany w okrąg zielony. Na tym okręgu opisano trójkąt DEF tak, żeby punkty A, B, C były punktami styczności. Następnie opisano okrąg niebieski na trójkącie DEF i opisano trójkąt GHI na tym okręgu tak, żeby punkty D, E, F były punktami styczności. Jakie warunki muszą spełniać kąty trójkąta ABC, żeby opisana konstrukcja była możliwa?

R1RHsoePaMr32
Grafika przedstawia niebieski trójkąt ABC wpisany w okrąg o kolorze zielonym . Przez punkty A B i C przechodzą styczne które tworzą opisany na zielonym okręgu trójkąt o wierzchołkach DEF . Trójkąt DEF jest jednocześnie wpisany w niebieski okrąg. Na niebieskim okręgu opisano ciemnoniebieski trójkąt o wierzchołkach GHI który jest styczny do niebieskiego okręgu w punktach D, E i F.
Animacja
Dla nauczyciela