Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Różnica pól między kołami opisanym na trójkącie równobocznym i wpisanym w ten trójkąt jest równa $1$ . Oblicz pole trójkąta.

Niech $a$ , $h$ , $R$ , $r$ oznaczają odpowiednio długość boku trójkąta równobocznego, jego wysokość, promień okręgu opisanego i promień okręgu wpisanego w ten trójkąt. Wtedy $a = \frac{2}{\sqrt{3}} h$ , $R = \frac{2}{3} h$ oraz $R = 2 r$ .

Różnicę pól opisuje wyrażenie $π R^{2} - π r^{2} = 1$ .

Ponieważ $r = \frac{1}{2} R$ , więc $π R^{2} - π {(\frac{1}{2} R)}^{2} = 1$ .

Stąd $\frac{3 π}{4} R^{2} = 1$ , czyli $R = \sqrt{\frac{4}{3 π}}$ .

Pole trójkąta opisuje wzór $P_{△} = a^{2} \frac{\sqrt{3}}{4}$ , zatem $P_{△} = {(\frac{2}{\sqrt{3}} \cdot \frac{3}{2} \cdot \sqrt{\frac{4}{3 π}})}^{2} \cdot \frac{\sqrt{3}}{4} = \frac{\sqrt{3}}{π}$ .

$P_{△} = \frac{\sqrt{3}}{π}$ .

Ćwiczenie 2

Trójkątem spodkowym trójkąta $P Q R$ nazywamy trójkąt, którego wierzchołkami są spodki wysokości trójkąta $P Q R$ . Rozważmy trójkąt równoboczny $A B C$ i jego trójkąt spodkowy. Różnica długości promieni okręgów wpisanych w trójkąt $A B C$ i jego trójkąt spodkowy jest równa $\sqrt{3}$ . Oblicz obwód trójkąta $A B C$ .

Popatrzmy na rysunek.

R1EjjCCNZ3Ebv

Ilustracja przedstawia trójkąt równoboczny ABC. Zaznaczono wysokości trójkąta przecinające się w punkcie H. Punkty przecięcia z bokami połączono i otrzymano trójkąt.

Na wstępie należy zauważyć, że trójkąt spodkowy (ortyczny) trójkąta równobocznego jest także trójkątem równobocznym, o boku dwa razy krótszym. Niech $a$ , $h$ , $R$ , $r$ oznaczają odpowiednio długość boku trójkąta równobocznego $A B C$ , jego wysokość, promień okręgu opisanego i promień okręgu wpisanego w ten trójkąt, a $r_{s}$ niech oznacza promień okręgu wpisanego w trójkąt spodkowy.

Wtedy: $r_{s} = \frac{1}{2} r$ , stąd $r - r_{s} = r - \frac{1}{2} r = \frac{1}{2} r = \sqrt{3}$ , czyli $r = 2 \sqrt{3}$

Obwód trójkąta $A B C$ jest więc równy $3 \cdot a = 3 \cdot (\frac{2}{\sqrt{3}} \cdot 3 r) = 3 \cdot (\frac{2}{\sqrt{3}} \cdot 3 \cdot (2 \sqrt{3})) = 36$ .

Obwód trójkąta jest równy $36$ .

R1Uu7x2chhcnE1

Ćwiczenie 3

Ćwiczenie 4

W trójkącie równobocznym $A B C$ o boku długości $a$ poprowadzono wysokość $A D$ oraz odcinek $D E$ łączący środki dwóch boków tego trójkąta, jak na rysunku.

R1duZ2HnvkNP8

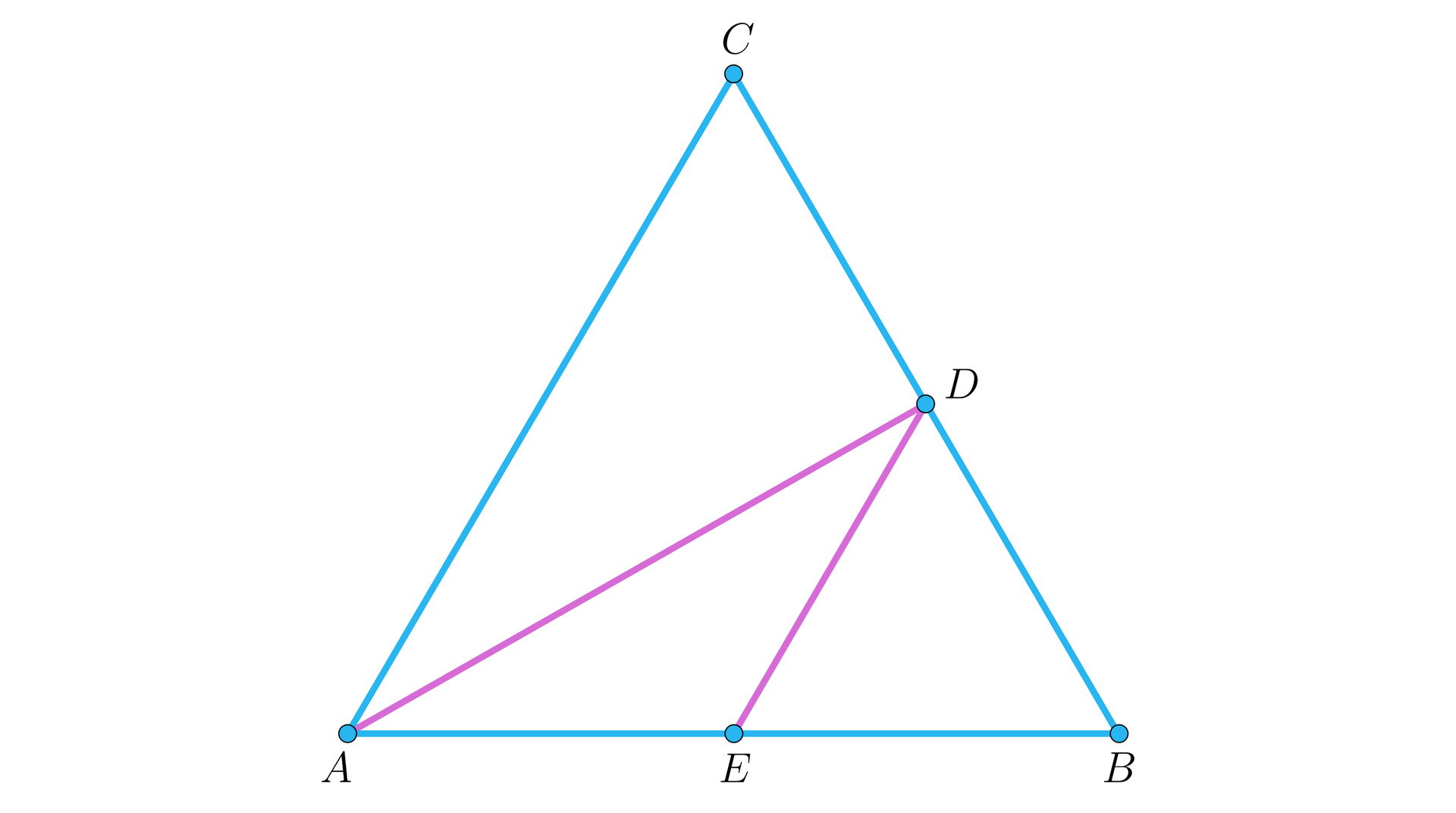
Ilustracja przedstawia trójkąt ABC. Poprowadzono wysokość AD oraz odcinek DE łączący środki boku BC oraz podstawy AB.

Promień okręgu wpisanego w trójkąt $E B D$ jest równy $1$ Oblicz promień okręgu wpisanego w trójkąt $A E D$ .

Trójkąt $E B D$ jest trójkątem równobocznym o boku $\frac{1}{2} a$ . Ponieważ promień okręgu wpisanego w ten trójkąt jest równy $1$ , więc $\frac{1}{2} a = \frac{2}{\sqrt{3}} \cdot (3 \cdot 1) = 2 \sqrt{3}$ , stąd $a = 4 \sqrt{3}$ .

Pole trójkąta $A E D$ jest jedną czwartą pola trójkąta $A B C$ , czyli jest równe $P_{A E D} = \frac{a^{2} \sqrt{3}}{16} = \frac{{(4 \sqrt{3})}^{2} \sqrt{3}}{16} = 3 \sqrt{3}$ .

Oznaczmy przez $r_{A E D}$ szukany promień, wtedy $P_{A E D} = \frac{|A E| + |E D| + |A D|}{2} \cdot r_{A E D}$ , czyli $3 \sqrt{3} = \frac{\frac{1}{2} a + \frac{1}{2} a + a \frac{\sqrt{3}}{2}}{2} \cdot r_{A E D} = \frac{2 \sqrt{3} + 2 \sqrt{3} + 6}{2} \cdot r_{A E D}$ , zatem $r_{A E D} = \frac{3 \sqrt{3}}{2 \sqrt{3} + 3} = 6 - 3 \sqrt{3}$

$r_{A E D} = 6 - 3 \sqrt{3}$

Ćwiczenie 5

Ri4wyDo1ivcPF

R1QxCPe12xUJC

Oznaczmy przez H ortocentrum, przez A indeks dolny, jeden, koniec indeksu dolnego, B indeks dolny, jeden, koniec indeksu dolnego, C indeks dolny, jeden, koniec indeksu dolnego odpowiednie spodki wysokości trójkąta równobocznego A B C a przez P punkt wspólny okręgu wpisanego i wysokości C C indeks dolny, jeden, koniec indeksu dolnego tego trójkąta. Na kolejnych rysunkach podano długość jednego z odcinków, wyróżnionego kolorem. Korzystając z danych podanych na rysunkach wyznacz długości R i r promieni okręgów opisanego i wpisanego w ten trójkąt.
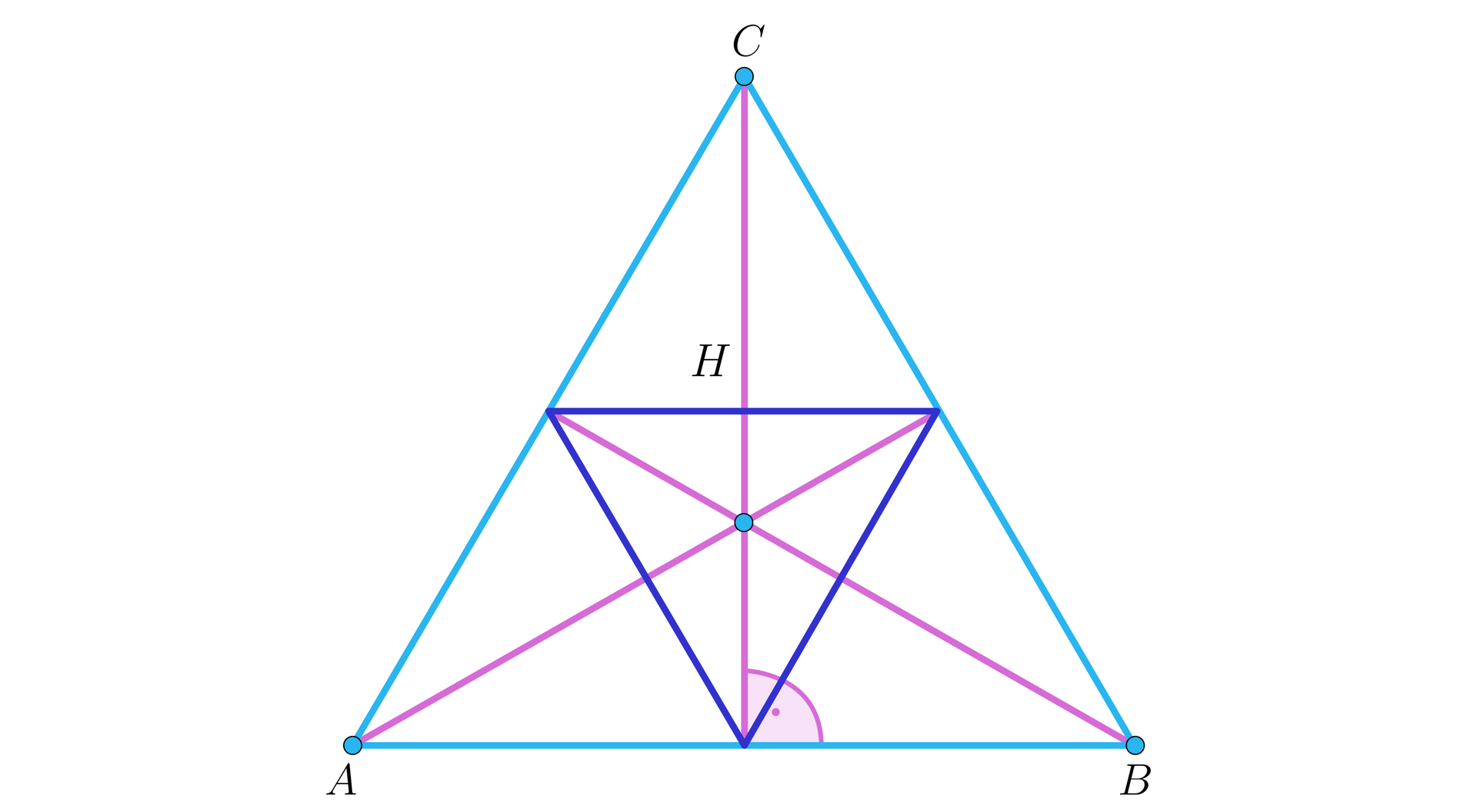
Dopasuj zależności do odpowiedniego opisu. r, równa się, początek ułamka, cztery pierwiastek kwadratowy z trzy, mianownik, trzy, koniec ułamka, R, równa się, początek ułamka, osiem pierwiastek kwadratowy z trzy, mianownik, trzy, koniec ułamka Możliwe odpowiedzi: 1. Ilustracja przedstawia okrąg wpisany w trójkąt ABC oraz opisany na nim. Zaznaczono wysokości A A indeks dolny 1 koniec indeksu, B B indeks dolny 1 koniec indeksu, C C indeks dolny 1 koniec indeksu. Przecinają się one w punkcie H będącym środkiem okręgu. Punkt P jest miejscem przecięcia okręgu wpisanego w trójkąt z wysokością C C indeks dolny 1 koniec indeksu. Odcinek P B indeks dolny 1 koniec indeksu ma długość trzy., 2. Ilustracja przedstawia okrąg wpisany w trójkąt ABC oraz opisany na nim. Zaznaczono wysokości A A indeks dolny 1 koniec indeksu, B B indeks dolny 1 koniec indeksu, C C indeks dolny 1 koniec indeksu. Przecinają się one w punkcie H będącym środkiem okręgu. Zaznaczono odcinek A indeks dolny 1 koniec indeksu C indeks dolny 1 koniec indeksu mający długość dwa pierwiastek kwadratowy z trzy., 3. Ilustracja przedstawia okrąg wpisany w trójkąt ABC oraz opisany na nim . Zaznaczono wysokości A A indeks dolny 1 koniec indeksu, B B indeks dolny 1 koniec indeksu, C C indeks dolny 1 koniec indeksu. Przecinają się one w punkcie H będącym środkiem okręgu. Zaznaczono odcinek C indeks dolny 1 koniec indeksu B mający długość cztery. r, równa się, dwa, R, równa się, cztery Możliwe odpowiedzi: 1. Ilustracja przedstawia okrąg wpisany w trójkąt ABC oraz opisany na nim. Zaznaczono wysokości A A indeks dolny 1 koniec indeksu, B B indeks dolny 1 koniec indeksu, C C indeks dolny 1 koniec indeksu. Przecinają się one w punkcie H będącym środkiem okręgu. Punkt P jest miejscem przecięcia okręgu wpisanego w trójkąt z wysokością C C indeks dolny 1 koniec indeksu. Odcinek P B indeks dolny 1 koniec indeksu ma długość trzy., 2. Ilustracja przedstawia okrąg wpisany w trójkąt ABC oraz opisany na nim. Zaznaczono wysokości A A indeks dolny 1 koniec indeksu, B B indeks dolny 1 koniec indeksu, C C indeks dolny 1 koniec indeksu. Przecinają się one w punkcie H będącym środkiem okręgu. Zaznaczono odcinek A indeks dolny 1 koniec indeksu C indeks dolny 1 koniec indeksu mający długość dwa pierwiastek kwadratowy z trzy., 3. Ilustracja przedstawia okrąg wpisany w trójkąt ABC oraz opisany na nim . Zaznaczono wysokości A A indeks dolny 1 koniec indeksu, B B indeks dolny 1 koniec indeksu, C C indeks dolny 1 koniec indeksu. Przecinają się one w punkcie H będącym środkiem okręgu. Zaznaczono odcinek C indeks dolny 1 koniec indeksu B mający długość cztery. r, równa się, trzy, R, równa się, sześć Możliwe odpowiedzi: 1. Ilustracja przedstawia okrąg wpisany w trójkąt ABC oraz opisany na nim. Zaznaczono wysokości A A indeks dolny 1 koniec indeksu, B B indeks dolny 1 koniec indeksu, C C indeks dolny 1 koniec indeksu. Przecinają się one w punkcie H będącym środkiem okręgu. Punkt P jest miejscem przecięcia okręgu wpisanego w trójkąt z wysokością C C indeks dolny 1 koniec indeksu. Odcinek P B indeks dolny 1 koniec indeksu ma długość trzy., 2. Ilustracja przedstawia okrąg wpisany w trójkąt ABC oraz opisany na nim. Zaznaczono wysokości A A indeks dolny 1 koniec indeksu, B B indeks dolny 1 koniec indeksu, C C indeks dolny 1 koniec indeksu. Przecinają się one w punkcie H będącym środkiem okręgu. Zaznaczono odcinek A indeks dolny 1 koniec indeksu C indeks dolny 1 koniec indeksu mający długość dwa pierwiastek kwadratowy z trzy., 3. Ilustracja przedstawia okrąg wpisany w trójkąt ABC oraz opisany na nim . Zaznaczono wysokości A A indeks dolny 1 koniec indeksu, B B indeks dolny 1 koniec indeksu, C C indeks dolny 1 koniec indeksu. Przecinają się one w punkcie H będącym środkiem okręgu. Zaznaczono odcinek C indeks dolny 1 koniec indeksu B mający długość cztery.

RXJ4Y1GH0Zy3o2

Ćwiczenie 6

Niech $R$ , $r$ oznaczają odpowiednio promień okręgu opisanego i promień okręgu wpisanego w ten sam trójkąt równoboczny. Liczby $R - r$ , $R \cdot r$ , $R + r$ tworzą w podanej kolejności ciąg arytmetyczny. Wtedy

$R = 1$
$R = 2$
$R = 3$
$R = 4$

Ćwiczenie 7

Rozważmy dowolny trójkąt $A B C$ . Na zewnątrz tego trójkąta, na jego bokach $A B$ , $A C$ i $B C$ zbudowano trójkąty równoboczne $A B R$ , $A C P$ i $B C Q$ . Okręgi opisane na trójkątach $A C P$ i $B C Q$ przecinają się w punktach $C$ , $S$ , jak na rysunku.

R896Co8yxliVx

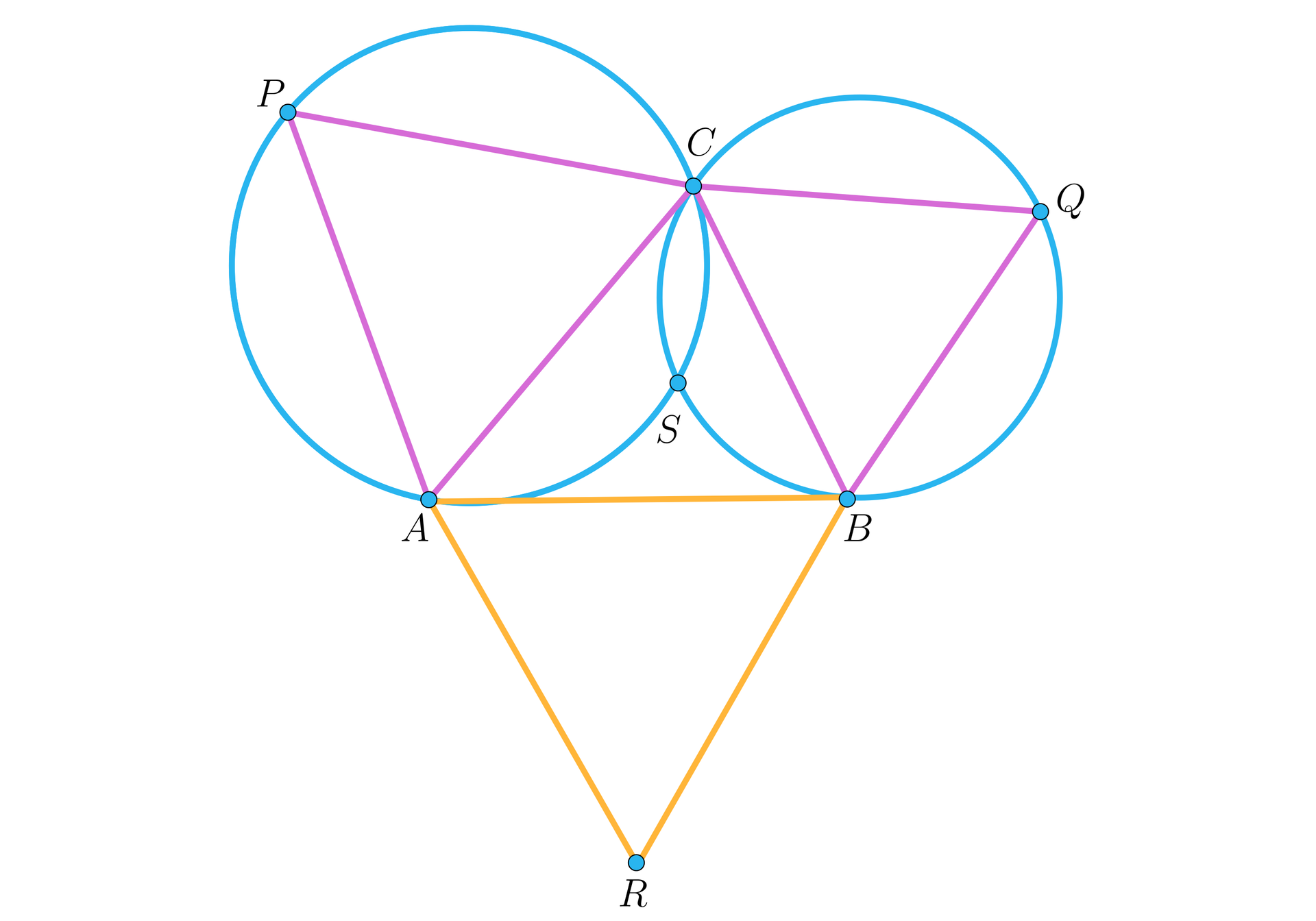
Ilustracja przedstawia trójkąt ABC. Na zewnątrz tego trójkąta, na jego bokach AB, AC i BC zbudowano trójkąty równoboczne ABR, ACP i BCQ. Okręgi opisane na trójkątach ACP i BCQ przecinają się w punktach C, S.

RUSZoFCihipGS

Uzasadnij, że okrąg opisany na trójkącie

A B R

przechodzi przez punkt

S

.
Ułóż w prawidłowej kolejności etapy dowodu. Elementy do uszeregowania: 1. Korzystając ponownie z twierdzenia o czworokącie opisanym na okręgu otrzymujemy, że na czworokącie

A R B S

da się opisać okrąg., 2. Zauważmy, że

|∢ A S B| = 360 ° - |∢ A S C| - |∢ B S C| = 360 ° - 120 ° - 120 ° = 120 °

., 3. Analogicznie, ponieważ czworokąt

B Q C S

da się wpisać w okrąg, więc

|∢ B S C| = 180 ° - |∢ B Q C| = 120 °

., 4. Rozważmy czworokąt

A S C P

. Z twierdzenia o czworokącie wpisanym w okrąg wynika, że

|∢ A S C| = 180 ° - |∢ A P C| = 120 °

., 5. Zbadajmy teraz kąty w czworokącie

A R B S

., 6. Zauważmy, że na każdym z czworokątów

A S C P

oraz

B Q C S

da się opisać okręgi., 7. W szczególności otrzymujemy:

|∢ A R B| + |∢ A S B| = 60 ° + 120 ° = 180 °

., 8. To kończy dowód.

Uzasadnij, że okrąg opisany na trójkącie $A B R$ przechodzi przez punkt $S$ .
Ułóż w kolejności etapy dowodu.

Korzystając ponownie z twierdzenia o czworokącie opisanym na okręgu otrzymujemy, że na czworokącie $A R B S$ da się opisać okrąg.
Zauważmy, że $"|"∢ A S B"|" = 360 ° - "|"∢ A S C"|" - "|"∢ B S C"|" = 360 ° - 120 ° - 120 ° = 120 °$ .
Zbadajmy teraz kąty w czworokącie $A R B S$ .
Zauważmy, że na każdym z czworokątów $A S C P$ oraz $B Q C S$ da się opisać okręgi.
Rozważmy czworokąt $A S C P$ . Z twierdzenia o czworokącie wpisanym w okrąg wynika, że $"|"∢ A S C"|" = 180 ° - "|"∢ A P C"|" = 120 °$ .
Analogicznie, ponieważ czworokąt $B Q C S$ da się wpisać w okrąg, więc $"|"∢ B S C"|" = 180 ° - "|"∢ B Q C"|" = 120 °$ .
W szczególności otrzymujemy: $"|"∢ A R B"|" + "|"∢ A S B"|" = 60 ° + 120 ° = 180 °$ .
To kończy dowód.

RR6EBlMb3UX8L3

Ćwiczenie 8

Symulacja interaktywna

Dla nauczyciela