Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Oblicz promień okręgu stycznego zewnętrznie do trzech parami stycznych zewnętrznie okręgów, których promienie są odpowiednio równe: $1$ , $2$ , $3$ , jak na rysunku.

R14MYtOx3Oq7z

Rysunek przedstawia trzy okręgi parami styczne o promieniach kolejno: 1, 2, 3. Między ich środkami wyrysowano trójkąt prostokątny. Z każdego kąta tego trójkąta narysowano linią przerywaną dwusieczną, a punkt ich przecięcia jest środkiem czwartego okręgu stycznego do pozostałych trzech okręgów.

Środki trzech okręgów tworzą trójkąt prostokątny. Szukany okrąg jest styczny zewnętrznie do danych okręgów, jak na rysunku.

RhM2xREIWpDsB

Oznaczmy przez $x$ , $y$ , $r$ odpowiednio odległości środka okręgu od przyprostokątnych oraz szukany promień.

Wtedy możemy zastosować trzykrotnie twierdzenie Pitagorasa otrzymując równania: $x^{2} + y^{2} = {(1 + r)}^{2}$ , ${(4 - x)}^{2} + y^{2} = {(3 + r)}^{2}$ , $x^{2} + {(3 - y)}^{2} = {(2 + r)}^{2}$ .

Odejmując parami odpowiednie równania dostajemy: $16 - 8 x = 4 r + 8$ , $9 - 6 y = 2 r + 3$ .

Wyznaczając niewiadome $x$ , $y$ i wstawiając do pierwszego z równań otrzymujemy: ${(1 - \frac{r}{2})}^{2} + {(1 - \frac{r}{3})}^{2} = {(1 + r)}^{2}$ .

Stąd $r = \frac{6}{23}$ .

Ćwiczenie 2

Trzy okręgi o promieniach odpowiednio $1$ , $2$ , $3$ są parami styczne zewnętrznie. Ich środki są wierzchołkami trójkąta. Oblicz promień okręgu wpisanego w ten trójkąt.

Skonstruujmy rysunek ilustrujący zadanie.

R17yIrc0ZlLS0

Rysunek przedstawia trzy okręgi parami styczne o promieniach kolejno: 1, 2, 3. Między ich środkami wyrysowano trójkąt prostokątny.

Z rysunku możemy wywnioskować, że boki naszego trójkąta mają odpowiednio długości: $3$ , $4$ , $5$ , a to oznacza, że trójkąt ten jest trójkątem prostokątnym. Zatem promień $r$ okręgu wpisanego jest równy: $r = \frac{3 + 4 - 5}{2} = 1$ .

R15rsXPdqgp9U2

Ćwiczenie 3

Dostępne opcje do wyboru: zależy od długości

r_{1}

r_{2}

, jest równa

7

, jest równa

28

, jest równa

14

. Polecenie: Przeciągnij poprawną odpowiedź. Dwa okręgi o środkach w punktach

O_{1}

O_{2}

i promieniach odpowiednio

r_{1}

r_{2}

są styczne wnętrznie. Środek większego okręgu o promieniu

14

leży na prostej

O_{1} O_{2}

. Mniejszy okrąg przechodzi przez środek większego okręgu.

Odległość

|O_{1} O_{2}|

luka do uzupełnienia .

Przeciągnij poprawną odpowiedź.

jest równa $28$ , jest równa $14$ , zależy od długości $r_{1}$ i $r_{2}$ , jest równa $7$

Dwa okręgi o środkach w punktach $O_{1}$ i $O_{2}$ i promieniach odpowiednio $r_{1}$ i $r_{2}$ są styczne wnętrznie. Środek większego okręgu o promieniu $14$ leży na prostej $O_{1} O_{2}$ . Mniejszy okrąg przechodzi przez środek większego okręgu.

Odległość $"|"O_{1} O_{2}"|"$ .

RvVa8OGMssIwh2

Ćwiczenie 4

Dwa okręgi o środkach w punktach $O_{1}$ i $O_{2}$ i promieniach odpowiednio $r_{1}$ i $r_{2}$ , gdzie $r_{1} < r_{2}$ , są wewnętrznie styczne. Sieczna obu okręgów, przechodząca przez punkt styczności $P$ tych okręgów i przez środek $O_{1}$ , przecięła okrąg o środku $O_{2}$ w punkcie $Q \neq P$ . Jeśli $"|"O_{1} O_{2}"|" = 5$ , $"|"P Q"|" = 14$ , to promienie tych okręgów są równe:

$r_{1} = 2, r_{2} = 7$
$r_{1} = 7, r_{2} = 7$
$r_{1} = 5, r_{2} = 9$
$r_{1} = 4, r_{2} = 5$

Ćwiczenie 5

Dwa współśrodkowe okręgi o promieniach $r_{1} = 10$ , $r_{2} = 17$ przecięto wspólną sieczną, której odległość od środków tych okręgów jest równa $8$ . Oblicz długość każdego z odcinków tej siecznej, zawartych między tymi okręgami.

Na rysunku przedstawiono dwa trójkąty prostokątne, wyznaczone przez promienie i połowy odpowiednich cięciw.

R5Hi4dwmn8bNs

Rysunek przedstawia dwa okręgi o wspólnym środku S. Okręgi przecina poziomy odcinek w taki sposób, że odległość od środka S do odcinka jest mniejsza, niż promień mniejszego okręgu. Odległość ta zaznaczona jest linią przerywaną. Z punktu S poprowadzone są linią przerywaną promienie obu okręgów w taki sposób, że ich końce znajdują w punktach przecięcia odcinka i tych okręgów.

Z twierdzenia Pitagorasa, zastosowanego do każdego z tych trójkątów, wynika w szczególności:

$8^{2} + x^{2} = 10^{2}$ oraz $8^{2} + y^{2} = 17^{2}$ , gdzie każdy z szukanych odcinków siecznej ma długość $y - x$ .

Ponieważ $x = 6$ oraz $y = 15$ , więc długość tych odcinków jest równa $9$ .

Ćwiczenie 6

Odcinek o końcach $P$ , $Q$ ma długość $2$ . Z końców tego odcinka zakreślono łuki okręgów, o promieniu $2$ , aż do ich przecięcia w punkcie $S$ . Oblicz promień $r$ okręgu, który jest styczny wewnętrznie do zakreślonych łuków i do odcinka $P Q$ , jak na rysunku.

R5q3zsfCLenxj

R1GGyeAjYkDwl

Ułóż w kolejności odpowiednie etapy rozwiązania.

Możemy teraz zapisać równanie z niewiadomą $r$ : ${(2 - r)}^{2} = 1 + r^{2}$ .
Zauważmy, że $"|"P T"|" = 1$ , $"|"O T"|" = r$ oraz $"|"O R"|" = r$ .
Zatem promień okręgu jest równy: $r = \frac{3}{4}$ .
Oznaczmy przez $R$ i $T$ punkty styczności szukanego okręgu odpowiednio z łukiem $Q S$ i odcinkiem $P Q$ .
Ale $"|"P R"|" = 2$ , stąd $"|"P O"|" = "|"P R"|" - r = 2 - r$ .
Wtedy ${"|"P O"|"}^{2} = 1 + r^{2}$ oraz $"|"P R"|" = "|"P O"|" + r$ .
Po redukcji otrzymujemy $4 - 4 r = 1$ .

Podaj znane Ci sposoby na ustawienie dwóch okręgów o różnych promieniach względem siebie. W każdym przypadku opisz własnymi słowami w sposób ogólny, jaka jest odległość między ich środkami w stosunku do ich promieni: jest większa od ich sumy? Mniejsza? A może równa?

R1Af4aUJDIdJO3

Ćwiczenie 7

Zbadaj wzajemne położenie dwóch okręgów, mając dane odległość

|O_{1} O_{2}|

ich środków i promienie

r_{1}

r_{2}

. Dopasuj, łącząc w pary. Okręgi są styczne zewnętrznie. Możliwe odpowiedzi: 1.

|O_{1} O_{2}| = 10, r_{1} = 4, r_{2} = 5

, 2.

|O_{1} O_{2}| = 9, r_{1} = 2, r_{2} = 7

, 3.

|O_{1} O_{2}| = 11, r_{1} = 3, r_{2} = 15

, 4.

|O_{1} O_{2}| = 12, r_{1} = 3, r_{2} = 15

, 5.

|O_{1} O_{2}| = 8, r_{1} = 2, r_{2} = 4

Okręgi są styczne wewnętrznie. Możliwe odpowiedzi: 1.

|O_{1} O_{2}| = 10, r_{1} = 4, r_{2} = 5

, 2.

|O_{1} O_{2}| = 9, r_{1} = 2, r_{2} = 7

, 3.

|O_{1} O_{2}| = 11, r_{1} = 3, r_{2} = 15

, 4.

|O_{1} O_{2}| = 12, r_{1} = 3, r_{2} = 15

, 5.

|O_{1} O_{2}| = 8, r_{1} = 2, r_{2} = 4

Okręgi przecinają się w dwóch różnych punktach. Możliwe odpowiedzi: 1.

|O_{1} O_{2}| = 10, r_{1} = 4, r_{2} = 5

, 2.

|O_{1} O_{2}| = 9, r_{1} = 2, r_{2} = 7

, 3.

|O_{1} O_{2}| = 11, r_{1} = 3, r_{2} = 15

, 4.

|O_{1} O_{2}| = 12, r_{1} = 3, r_{2} = 15

, 5.

|O_{1} O_{2}| = 8, r_{1} = 2, r_{2} = 4

Każdy z okręgów leży na zewnątrz drugiego. Możliwe odpowiedzi: 1.

|O_{1} O_{2}| = 10, r_{1} = 4, r_{2} = 5

, 2.

|O_{1} O_{2}| = 9, r_{1} = 2, r_{2} = 7

, 3.

|O_{1} O_{2}| = 11, r_{1} = 3, r_{2} = 15

, 4.

|O_{1} O_{2}| = 12, r_{1} = 3, r_{2} = 15

, 5.

|O_{1} O_{2}| = 8, r_{1} = 2, r_{2} = 4

Jeden z okręgów leży wewnątrz drugiego. Możliwe odpowiedzi: 1.

|O_{1} O_{2}| = 10, r_{1} = 4, r_{2} = 5

, 2.

|O_{1} O_{2}| = 9, r_{1} = 2, r_{2} = 7

, 3.

|O_{1} O_{2}| = 11, r_{1} = 3, r_{2} = 15

, 4.

|O_{1} O_{2}| = 12, r_{1} = 3, r_{2} = 15

, 5.

|O_{1} O_{2}| = 8, r_{1} = 2, r_{2} = 4

Zbadaj wzajemne położenie dwóch okręgów, mając dane odległość $"|"O_{1} O_{2}"|"$ ich środków i promienie $r_{1}$ i $r_{2}$ . Dopasuj łącząc w pary.

Okręgi są styczne zewnętrznie.
Okręgi są styczne wewnętrznie.
Okręgi przecinają się w dwóch różnych punktach.
Każdy z okręgów leży na zewnątrz drugiego.
Jeden z okręgów leży wewnątrz drugiego.

Ćwiczenie 8

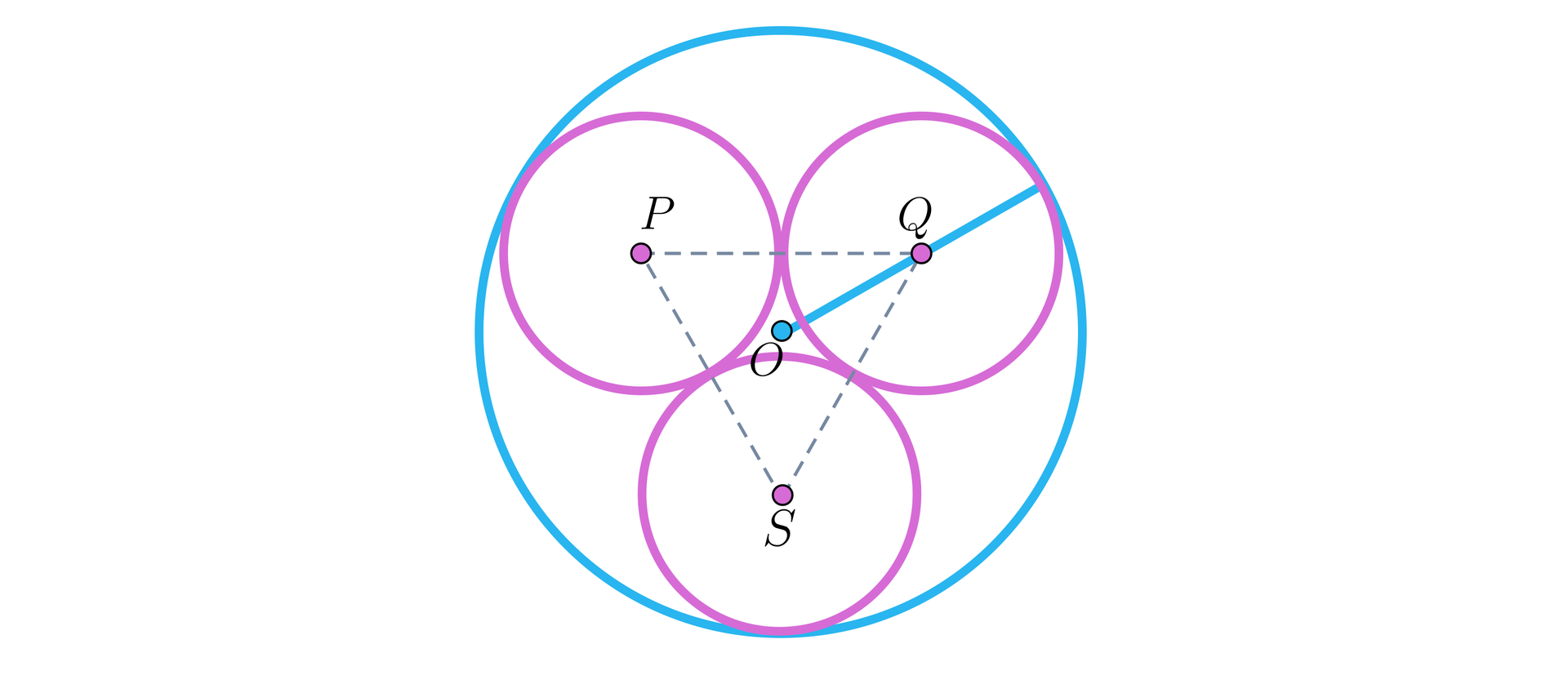
W dany okrąg o promieniu $R$ wpisano trzy okręgi o promieniu $r = 2 \sqrt{3} - 3$ w taki sposób, że wszystkie są wewnętrznie styczne do danego okręgu i każde dwa z nich są parami styczne zewnętrznie, jak na rysunku. Oblicz promień $R$ .

RlwLkXghyQagr

Rysunek przedstawia duży okrąg o środku w punkcie O i trzech mniejszych okręgach o takim samym promieniu, które są styczne wewnętrznie do dużego okręgu i jednocześnie są styczne zewnętrznie parami do siebie nawzajem. Środki małych okręgów znajdują się w punktach: P, Q, S, a pomiędzy nimi linią przerywaną wyrysowano trójkąt. Na rysunku zaznaczono także promień dużego koła, który przechodzi przez punkt Q.

Zauważmy, ze trójkąt $P Q S$ jest trójkątem równobocznym boku długości $2 r$ .

Odcinek $O Q$ ma długość $|O Q| = \frac{2}{3} \cdot (2 r) \cdot \frac{\sqrt{3}}{2} = \frac{2 r \sqrt{3}}{3}$ .

Ale $R = |O Q| + r = r \cdot \frac{3 + 2 \sqrt{3}}{3}$ .

Zatem $R = (2 \sqrt{3} - 3) \cdot \frac{3 + 2 \sqrt{3}}{3} = \frac{12 - 9}{3} = 1$ .

Aplet

Dla nauczyciela