Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

R1cLqgOcAikWp

Pole powierzchni całkowitej stożka o promieniu podstawy $r = 2$ i dwa razy dłuższej wysokości wynosi:

$P_{c} = 4 π + 4 \sqrt{5} π$
$P_{c} = 16 π$
$P_{c} = 12 π$

Ćwiczenie 2

R1dNzi1UfncBS

Zaznacz zdania prawdziwe.

Pole powierzchni całkowitej stożka, w którym wysokość ma długość $8$ , a promień podstawy $6$ wynosi $96 π$ .
Pole powierzchni całkowitej stożka, w którym przekrojem osiowym jest trójkąt równoboczny o boku $6$ wynosi $72 π$ .
Pole powierzchni całkowitej stożka, w którym długość promienia i wysokości są równe, a tworząca ma długość $4$ jest równe $4 π + 4 \sqrt{2} π$ .
Pole powierzchni całkowitej stożka, w którym promień podstawy stożka ma długość $2 \sqrt{2}$ , a wysokość jest trzy razy dłuższa wynosi $8 π + 8 \sqrt{10} π$ .

Ćwiczenie 3

R1IE1ufXDK0LJ

R9lnpPFbGinpi

Ćwiczenie 4

Na rysunkach 1 i 2 przedstawiono stożki.

R1WmRIOEYfgDW

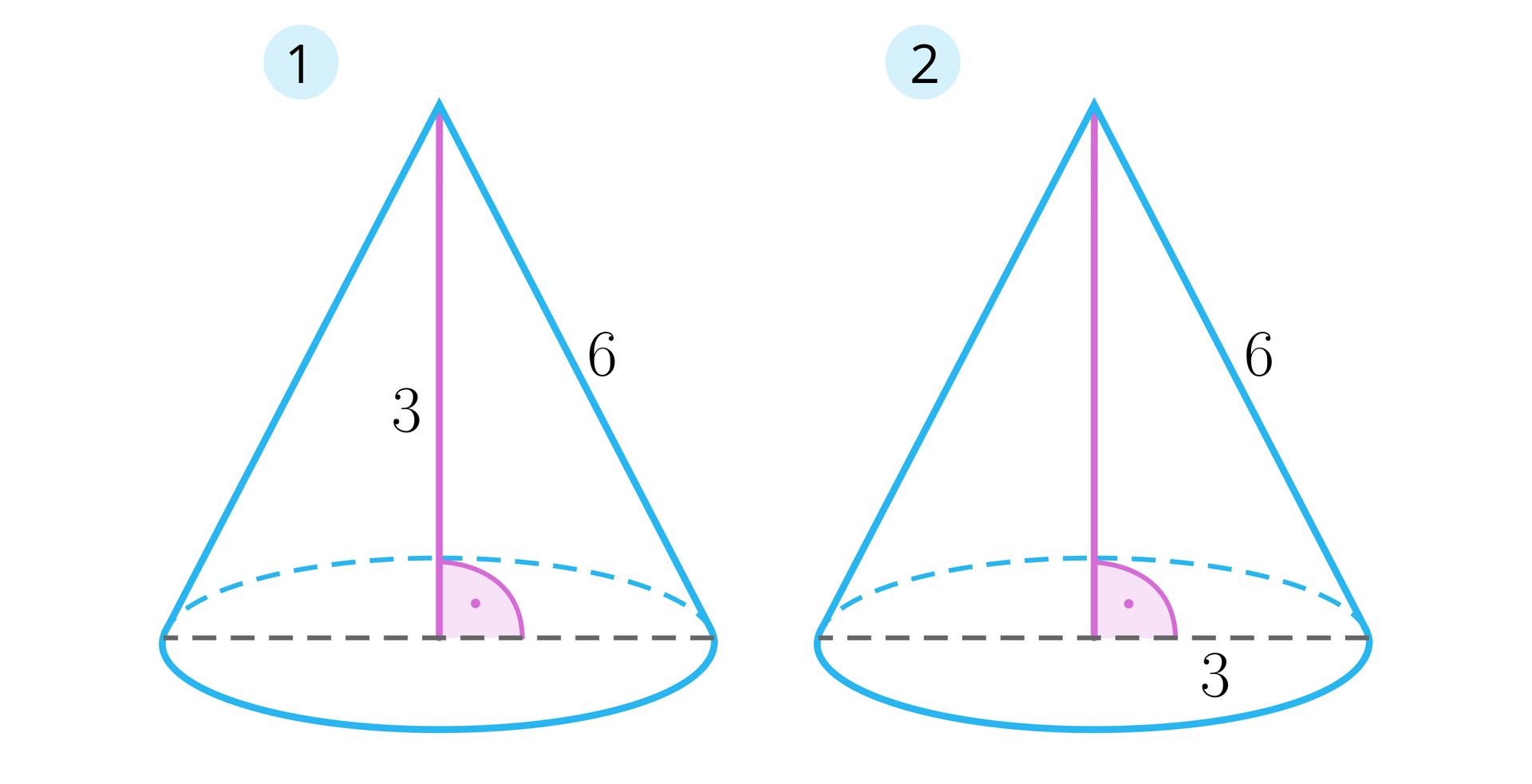
Ilustracja przedstawia dwa stożki, pierwszy z wysokością o długości trzy oraz tworzącą o długości sześć. Drugi z promieniem podstawy o długości trzy oraz tworzącą o długości sześć.

R174IKbvOV5HB

Pogrupuj elementy, zgodnie z podanym opisem. Własności stożka z rysunku

1

: Możliwe odpowiedzi: 1. pole podstawy jest równe

27 π

, 2. pole podstawy jest równe

9 π

, 3. pole powierzchni całkowitej jest równe

27 π + 18 \sqrt{3} π

, 4. pole powierzchni bocznej jest równe

18 π

, 5. pole powierzchni całkowitej jest równe

27 π

, 6. pole powierzchni bocznej jest równe

18 \sqrt{3} π

Własności stożka z rysunku

2

: Możliwe odpowiedzi: 1. pole podstawy jest równe

27 π

, 2. pole podstawy jest równe

9 π

, 3. pole powierzchni całkowitej jest równe

27 π + 18 \sqrt{3} π

, 4. pole powierzchni bocznej jest równe

18 π

, 5. pole powierzchni całkowitej jest równe

27 π

, 6. pole powierzchni bocznej jest równe

18 \sqrt{3} π

Pogrupuj elementy, zgodnie z podanym opisem.

pole podstawy jest równe <math><mn>9</mn><mi>π</mi></math>, pole powierzchni bocznej jest równe <math><mn>18</mn><mi>π</mi></math>, pole podstawy jest równe <math><mn>27</mn><mi>π</mi></math>, pole powierzchni całkowitej jest równe <math><mn>27</mn><mi>π</mi></math>, pole powierzchni całkowitej jest równe <math><mn>27</mn><mi>π</mi><mo>+</mo><mn>18</mn><msqrt><mn>3</mn></msqrt><mi>π</mi></math>, pole powierzchni bocznej jest równe <math><mn>18</mn><msqrt><mn>3</mn></msqrt><mi>π</mi></math>

Stożek z rysunku $1$ :
Stożek z rysunku $2$ :

Ćwiczenie 5

Rmn5WiSlruPOK

Wstaw w tekst odpowiednie liczby.

$2 π$ , $15 π$ , $20 π$ , $\frac{π}{4}$ , $36 π$

Pole powierzchni bocznej stożka, w którym długość promienia podstawy, wysokość oraz tworząca są kolejnymi liczbami naturalnymi wynosi .............

W stożku, w którym tworząca jest trzy razy większa od promienia podstawy a wysokość ma długość $2$ pole powierzchni wynosi .............

W stożku, w którym promień podstawy ma długość $2 \sqrt{3}$ a pole powierzchni bocznej jest dwa razy większe od pola podstawy, pole powierzchni całkowitej wynosi .............

Ćwiczenie 6

RORQnTvKoa1F6

Powierzchnia w kształcie koła w stożku.
Odcinek łączący dowolny punkt na brzegu podstawy stożka z jego wierzchołkiem.
Odległość wierzchołka od płaszczyzny podstawy stożka.
Jedno z działań, które występuje we wzorze na pole powierzchni całkowitej stożka.
Jego długość oznaczamy literą $r$ w stożku.
Tworzą go np. tworzące stożka.

1
2
3
4
5
6

Ćwiczenie 7

W stożku pole powierzchni bocznej jest $6$ razy większe od pola podstawy. Wyznacz pole powierzchni całkowitej w zależności od promienia podstawy $r$ .

Narysujmy stożek i wprowadźmy odpowiednie oznaczenia.

Rj8YIUWESr4P2

Ilustracja przedstawia stożek z promieniem podstawy o długości r, wysokością o długości h oraz tworzącą o długości l.

Z warunków zadania wynika, że $P_{b} = 6 \cdot P_{p}$ .

Zatem $π r l = 6 \cdot π r^{2}$ , czyli $l = 6 r$ .

Pole powierzchni całkowitej tego stożka jest równe:

$P_{c} = π r^{2} + π r \cdot 6 r = π r^{2} + 6 π r^{2} = 7 π r^{2}$ .

Ćwiczenie 8

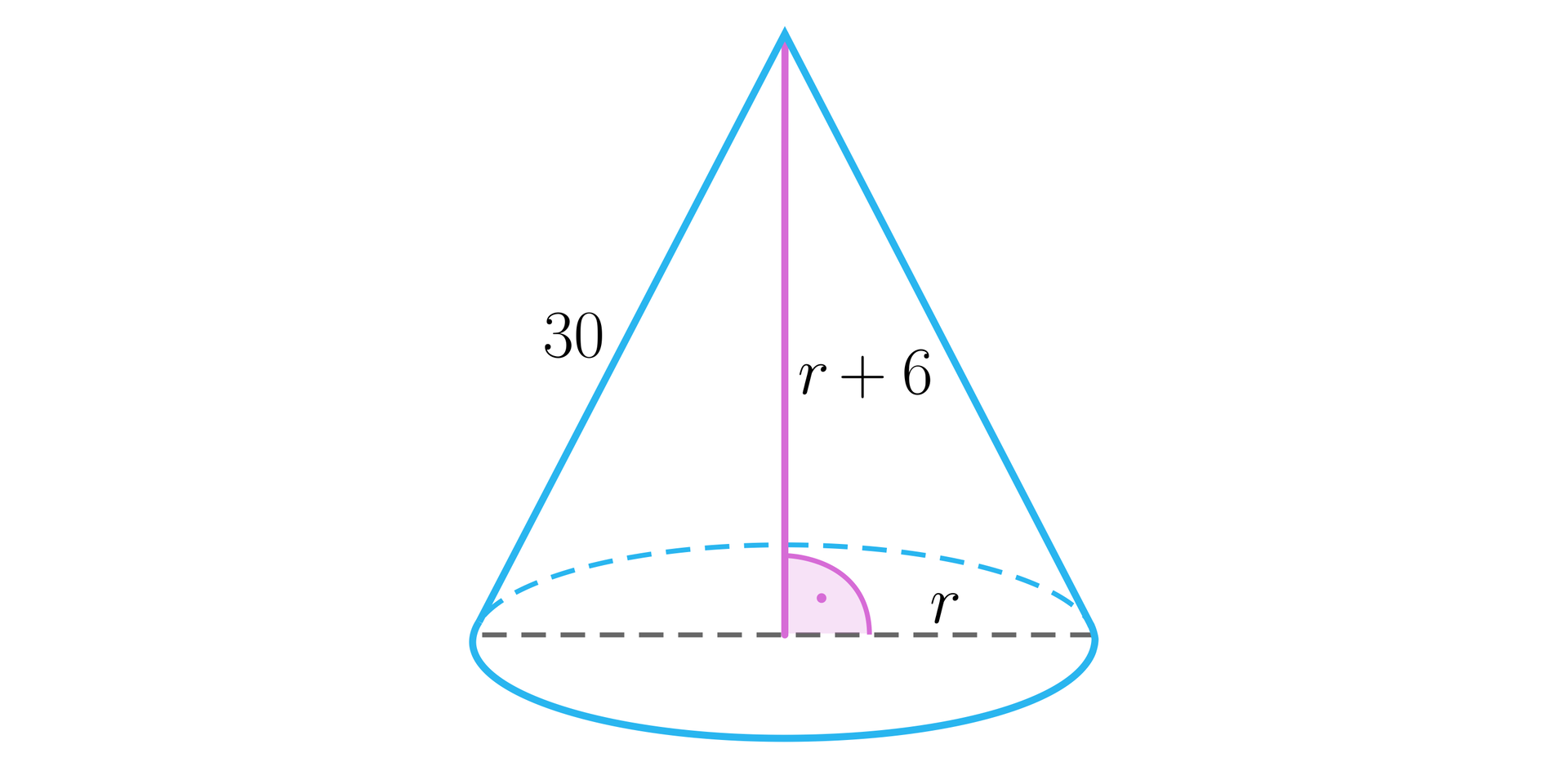
Tworząca stożka ma długość $30$ , a wysokość jest o $6$ dłuższa od promienia podstawy. Oblicz pole powierzchni całkowitej tego stożka.

Narysujmy stożek i wprowadźmy odpowiednie oznaczenia.

RMytaTVdWdFEB

Ilustracja przedstawia stożek z promieniem podstawy o długości r, wysokością o długości r dodać sześć oraz tworzącą o długości trzydzieści.

Ponieważ promień podstawy, wysokość oraz tworząca stożka tworzą trójkąt prostokątny, zatem do wyznaczenia wartości $r$ rozwiązujemy równanie:

$r^{2} + {(r + 6)}^{2} = 30^{2}$

$r^{2} + r^{2} + 12 r + 36 = 900$

$2 r^{2} + 12 r - 864 = 0$

$r^{2} + 6 r - 432 = 0$ .

Wobec tego $r = 18$ .

Pole powierzchni całkowitej tego stożka jest równe:

$P_{c} = π \cdot 18^{2} + π \cdot 18 \cdot 30 = 324 π + 540 π = 864 π$ .

Animacja 3D

Dla nauczyciela