Sprawdź się

Pokaż ćwiczenia:

R1Lwe431oains1

Ćwiczenie 1

RykmVTckQMDmp1

Ćwiczenie 2

Ćwiczenie 3

Zapoznaj się z pseudokodem.

Dijkstra(lista_sąsiedztwa, s):
	S ← utwórz pustą tablicę
    V ← utwórz tablicę i wypełnij ją wierzchołkami
    d ← utwórz pustą tablicę
    p ← utwórz pustą tablicę
    
	dla każdego elementu u w tablicy V: 
		d[u] ← ∞
		p[u] ← -1
        
	d[s] ← 0
    
	dopóki długość(V) > 0:
		najkrótsza_ścieżka ← ∞
		u ← -1
        
		dla każdego elementu v w tablicy V:
			jeśli najkrótsza_ścieżka > d[v]:
				najkrótsza_ścieżka ← d[v]
				u ← v
                
		S ← umieść element u na końcu tablicy
        V ← usuń element u z tablicy
        
		dla każdego elementu v w tablicy lista_sąsiadów[u]:
			jeśli d[v] > d[u] + w(u, v):
				d[v] ← d[u] + w(u, v)
				p[v] ← u
    
	zwróć d, p

R1V9oii3z4wXE1

Połącz w pary zmienne z ich zastosowaniami. prev[] Możliwe odpowiedzi: 1. wierzchołek dodawany do zbioru S unikalny dla każdej iteracji, 2. zbiór wszystkich wierzchołków grafu, 3. tablica kosztów dojścia do każdego wierzchołka, 4. zbiór wierzchołków, do których najmniejsze koszty dojścia zostały wyznaczone, 5. tablica przechowująca poprzedniki wierzchołków d[] Możliwe odpowiedzi: 1. wierzchołek dodawany do zbioru S unikalny dla każdej iteracji, 2. zbiór wszystkich wierzchołków grafu, 3. tablica kosztów dojścia do każdego wierzchołka, 4. zbiór wierzchołków, do których najmniejsze koszty dojścia zostały wyznaczone, 5. tablica przechowująca poprzedniki wierzchołków u Możliwe odpowiedzi: 1. wierzchołek dodawany do zbioru S unikalny dla każdej iteracji, 2. zbiór wszystkich wierzchołków grafu, 3. tablica kosztów dojścia do każdego wierzchołka, 4. zbiór wierzchołków, do których najmniejsze koszty dojścia zostały wyznaczone, 5. tablica przechowująca poprzedniki wierzchołków S Możliwe odpowiedzi: 1. wierzchołek dodawany do zbioru S unikalny dla każdej iteracji, 2. zbiór wszystkich wierzchołków grafu, 3. tablica kosztów dojścia do każdego wierzchołka, 4. zbiór wierzchołków, do których najmniejsze koszty dojścia zostały wyznaczone, 5. tablica przechowująca poprzedniki wierzchołków V Możliwe odpowiedzi: 1. wierzchołek dodawany do zbioru S unikalny dla każdej iteracji, 2. zbiór wszystkich wierzchołków grafu, 3. tablica kosztów dojścia do każdego wierzchołka, 4. zbiór wierzchołków, do których najmniejsze koszty dojścia zostały wyznaczone, 5. tablica przechowująca poprzedniki wierzchołków

Ćwiczenie 4

R121xONV2amtz11

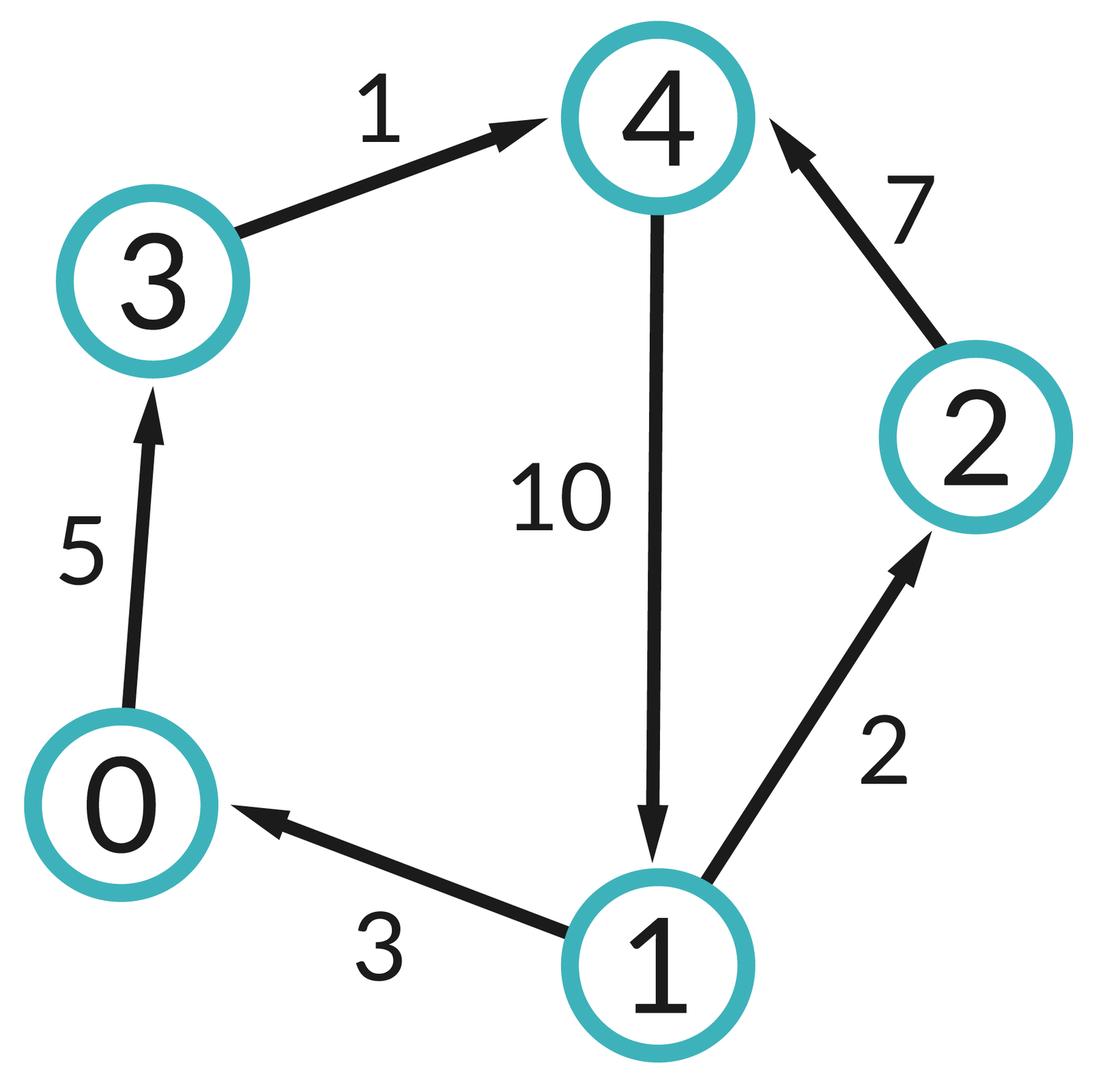
Graf składa się z pięciu wierzchołków. Tworzą one pięciokąt. Od wierzchołka jeden poprowadzone są dwie strzałki stanowiące krawędzie. Pierwsza o długości trzy prowadzi do wierzchołka zero, natomiast druga o długości dwa do wierzchołka dwa. Od wierzchołka dwa do wierzchołka cztery poprowadzona jest strzałka stanowiąca krawędź o długości siedem. Od wierzchołka zero do wierzchołka trzy poprowadzona jest strzałka odpowiadająca krawędzi o długości pięć. Od wierzchołka trzy do wierzchołka cztery poprowadzona jest strzałka stanowiąca krawędź o długości jeden. Od wierzchołka cztery do wierzchołka jeden poprowadzona jest strzałka odpowiadająca krawędzi o długości dziesięć.

Zapoznaj się z ilustracją pewnego grafu.

R6yQKO9eOISog

Wskaż wszystkie warianty tablic wyjściowych d i p, które może zwrócić algorytm Dijkstry dla zaprezentowanego grafu skierowanego.

Ćwiczenie 5

R1ZAFRCtw2K3d21

Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

R1T9CVAdBuM5g

Przyjmując za wierzchołek początkowy A, wskaż grafy, dla których algorytm Dijkstry nie zwróci poprawnego wyniku.

Ćwiczenie 6

RLXFIUBFbkS1X3

Źródło: Contentplus.pl sp. z o.o., licencja: CC BY-SA 3.0.

RfyTqO4Bi8JWf

Zapoznaj się poniższym opisem, a następnie wykonaj polecenie.
Graf składa się z sześciu wierzchołków oznaczonych od A do F. Wierzchołki połączone są krawędziami, tworzacymi sześciokąt. Ponadto dwie krawędzie zostały zaznaczone pomiędzy wierzchołkami wten sposób, że znajdują się w polu sześciokąta. Od wierzchołka A popdorwadzone sa dwie krawędzie do wierzchołka B o długości dziesięć i do wierzchołka C o długości sześć. Od wierzchołka B odchodzą dwie krawędzie. Pierwsza o długości cztery łączy go z wierzhcołkiem E, natomiast druga o długości dwa z wierzchołkiem F.Od wierzchołka C odchodzą dwie krawędzie. Pierwsza o długości siedem łączy wierzchołek C z wierzchołkiem D, natomiast druga o długości pięć z wierzchołkiem F. Warości dla krawędzi łączących odpowiednio wierzchołki D F oraz E F nie podano.
Wskaż długości ścieżek łączących, odpowiednio wierzchołki D F oraz E F, aby algorytm Dijkstry zwrócił następujący wynik:

d = { 6, 7, 0, 7, 6, 5 }, 
 p = { C, F, NULL, C, F, C }

Materiał źródłowy do ćwiczeń 7–8

RfxmdCBbLdQVn

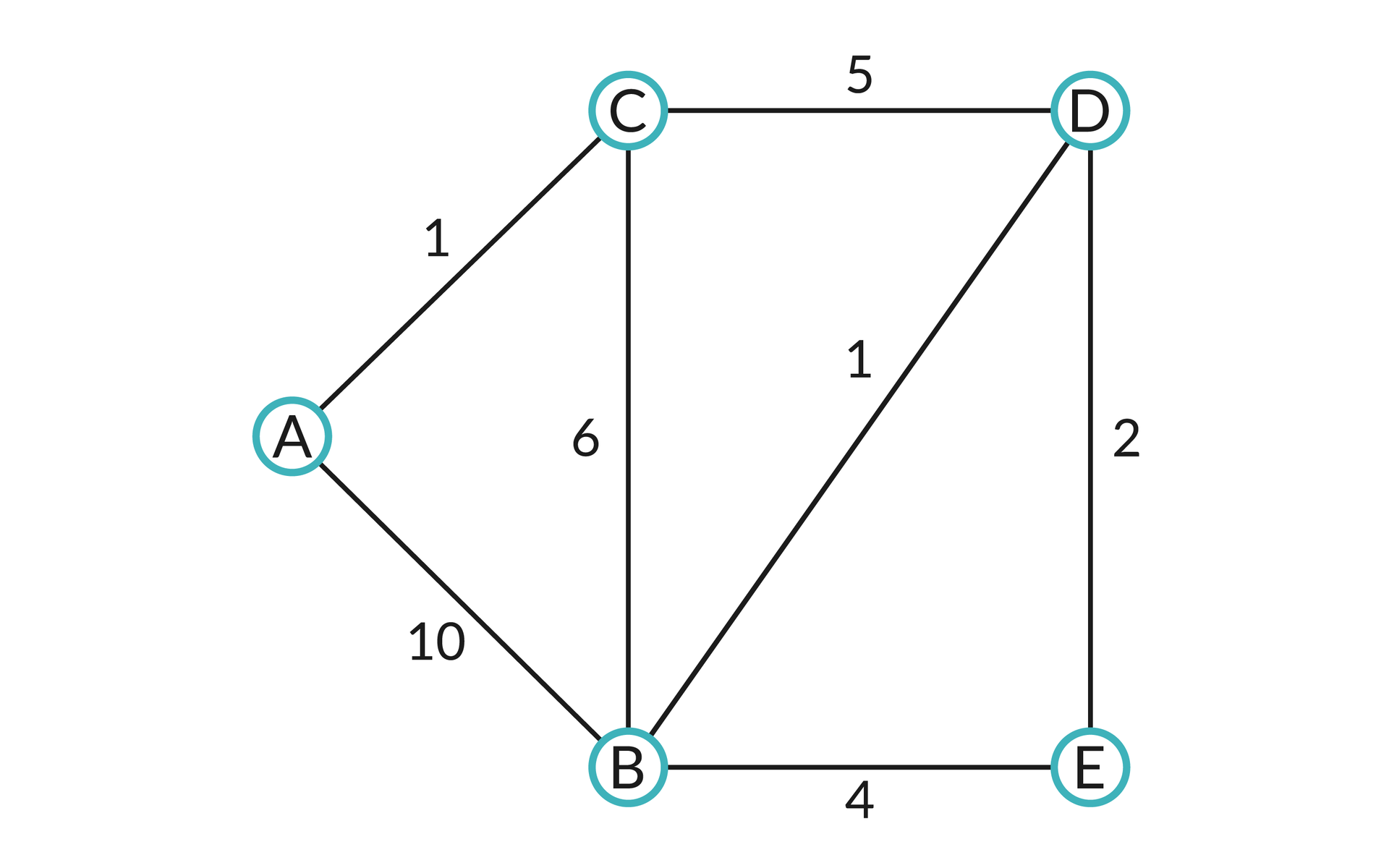
Ilustracja przedstawia graf z węzłami oznaczonymi literami oraz łączącymi je krawędziami oznaczone cyframi.
A, 1 C.
A, 10, B.
B, 6, C.
B, 4, E.
B, 1, D.
C, 5, D.
D, 2, E.

R14FJOhEMOPeV3

Ćwiczenie 7

W zaprezentowanym grafie s = E. Wskaż poprzednika, jeśli u = A.

R1Bw8dzhk9Lbs3

Ćwiczenie 8

W zaprezentowanym grafie s = A. Wskaż poprawną długość najkrótszej ścieżki, jaką należy pokonać, by od wierzchołka s dojść do wierzchołka u = B.

Prezentacja multimedialna

Dla nauczyciela