Sprawdź się
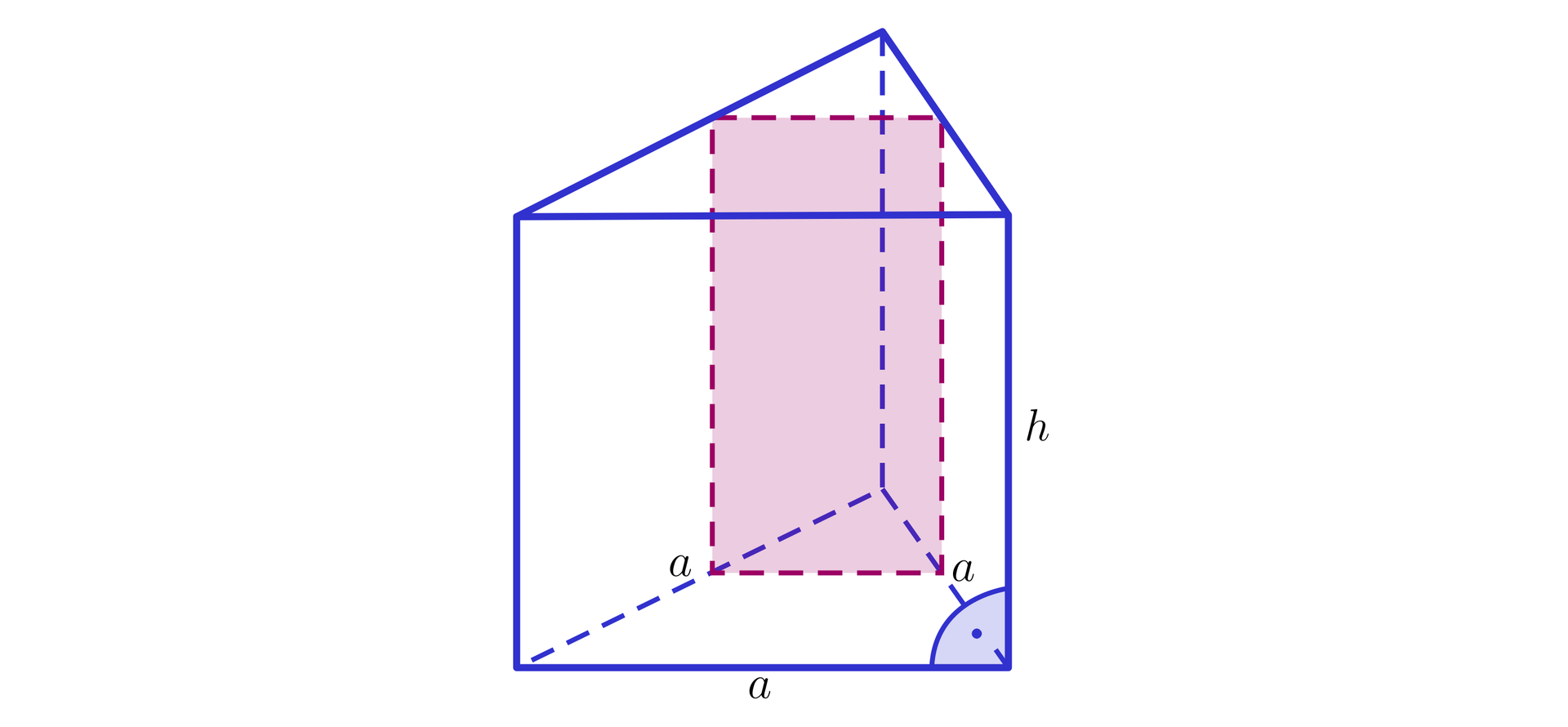
Na rysunku przedstawiono przekrój graniastosłupa prawidłowego trójkątnego płaszczyzną równoległą do podstawy. Jeżeli pole powierzchni całkowitej tego graniastosłupa jest równe , a krawędź boczna ma długość , to pole powierzchni przekroju jest równe:

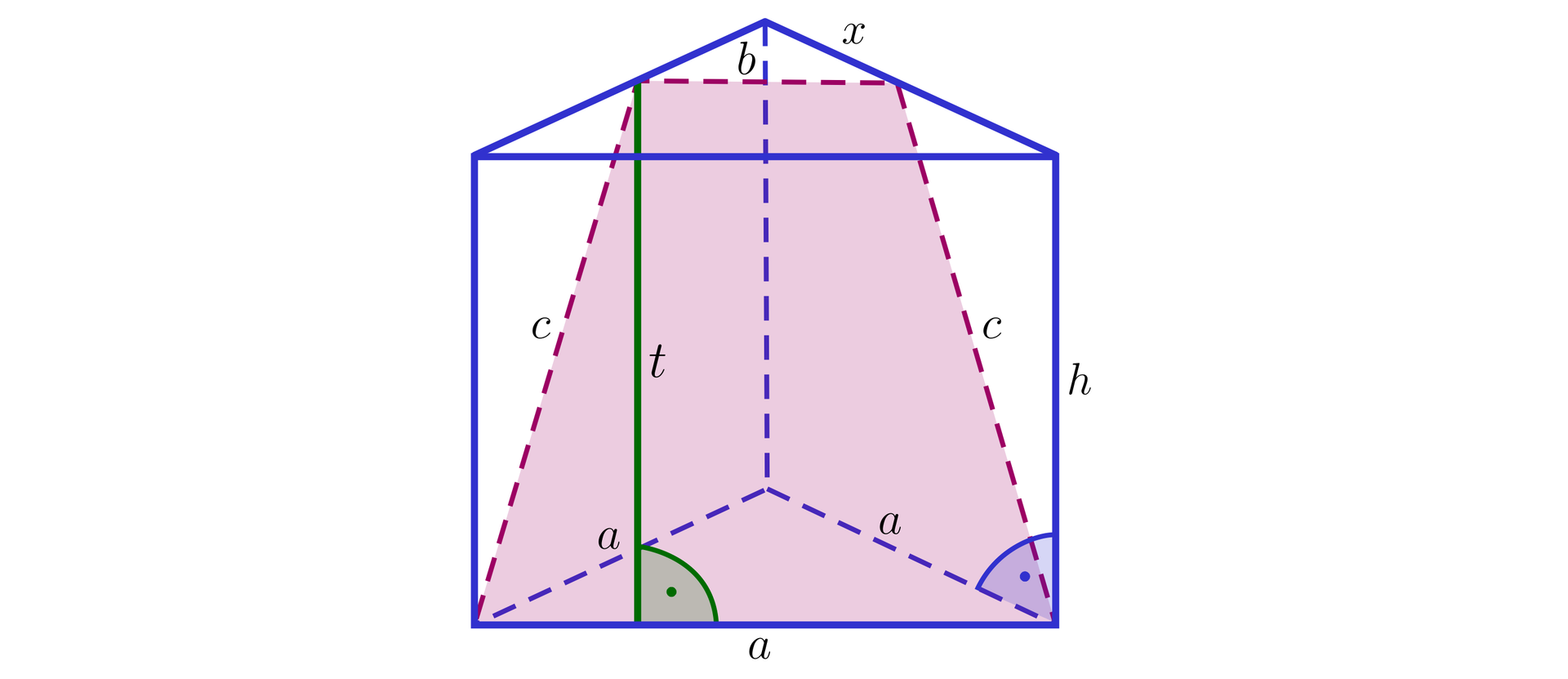
Na rysunku przedstawiono przekrój graniastosłupa prawidłowego trójkątnego płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej krawędzi bocznej.

Na rysunku przedstawiono przekrój graniastosłupa prawidłowego trójkątnego płaszczyzną przechodzącą przez wysokość podstawy i krawędź boczną.

Oblicz pole przekroju graniastosłupa prawidłowego trójkątnego, jeżeli płaszczyzna przekroju przechodzi przez krawędź dolnej podstawy i środki krawędzi górnej podstawy oraz krawędź podstawy ma długość , a krawędź boczna .
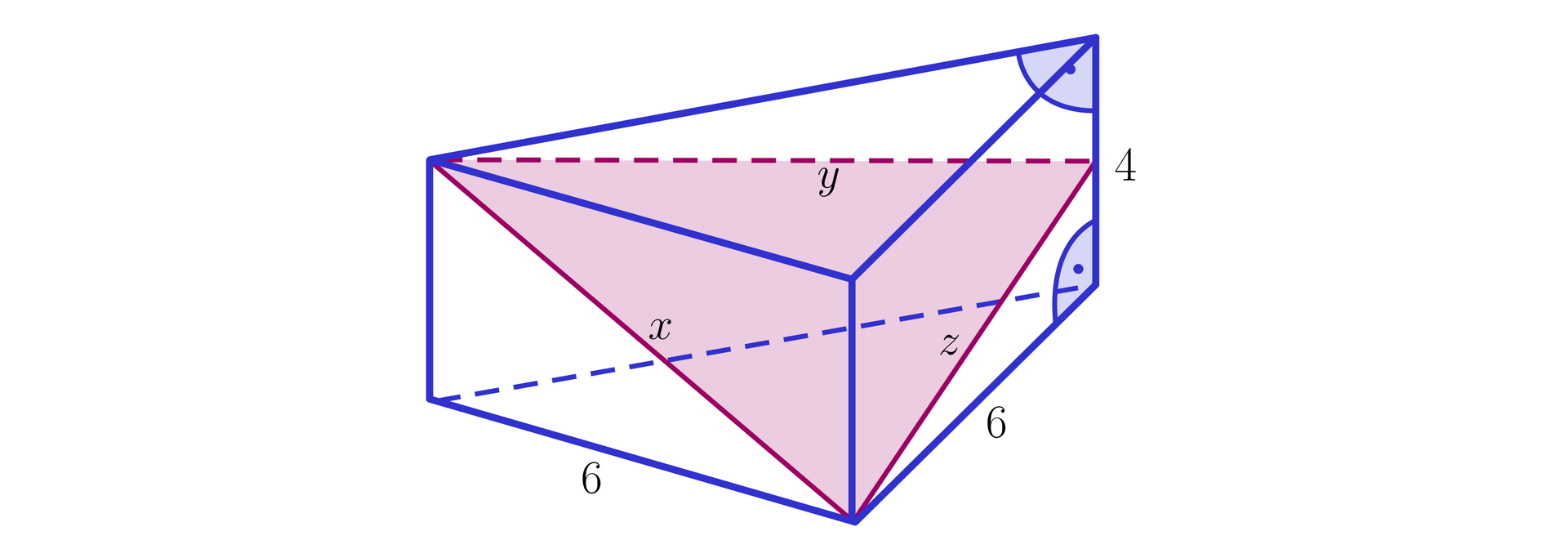
Na rysunku przedstawiono przekrój graniastosłupa prawidłowego trójkątnego pewną płaszczyzną.

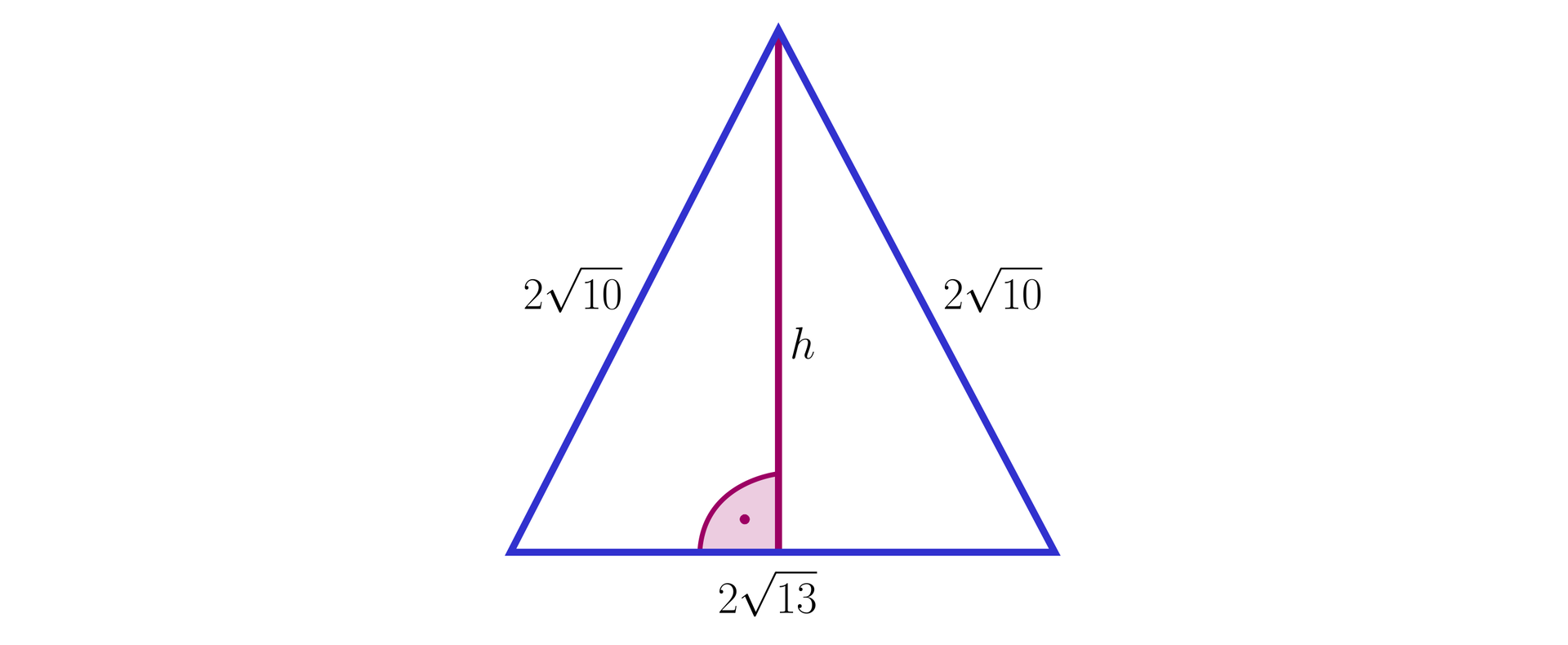
Wysokość trójkąta będącego przekrojem graniastosłupa prawidłowego trójkątnego z rysunku ma długość 1. , 2. , 3. , 4. , 5. .
Pole rozpatrywanego przekroju wynosi 1. , 2. , 3. , 4. , 5. .
Jeżeli wierzchołki prostokąta są środkami krawędzi podstaw graniastosłupa prawidłowego trójkątnego z rysunku, to:
Graniastosłup prawidłowy trójkątny przecięto płaszczyzną przechodzącą przez dwa wierzchołki oraz środek przeciwległej krawędzi bocznej, tak jak na poniższym rysunku. Oblicz pole otrzymanego przekroju, jeżeli krawędź podstawy graniastosłupa ma długość , a krawędź boczna ma długość .

Na rysunku przedstawiono przekrój graniastosłupa prawidłowego trójkątnego pewną płaszczyzną. Oblicz obwód oraz pole tego przekroju, jeżeli wszystkie krawędzie graniastosłupa mają długość .