Sprawdź się

Pokaż ćwiczenia:

RaTHIkNkmidYN1

Ćwiczenie 1

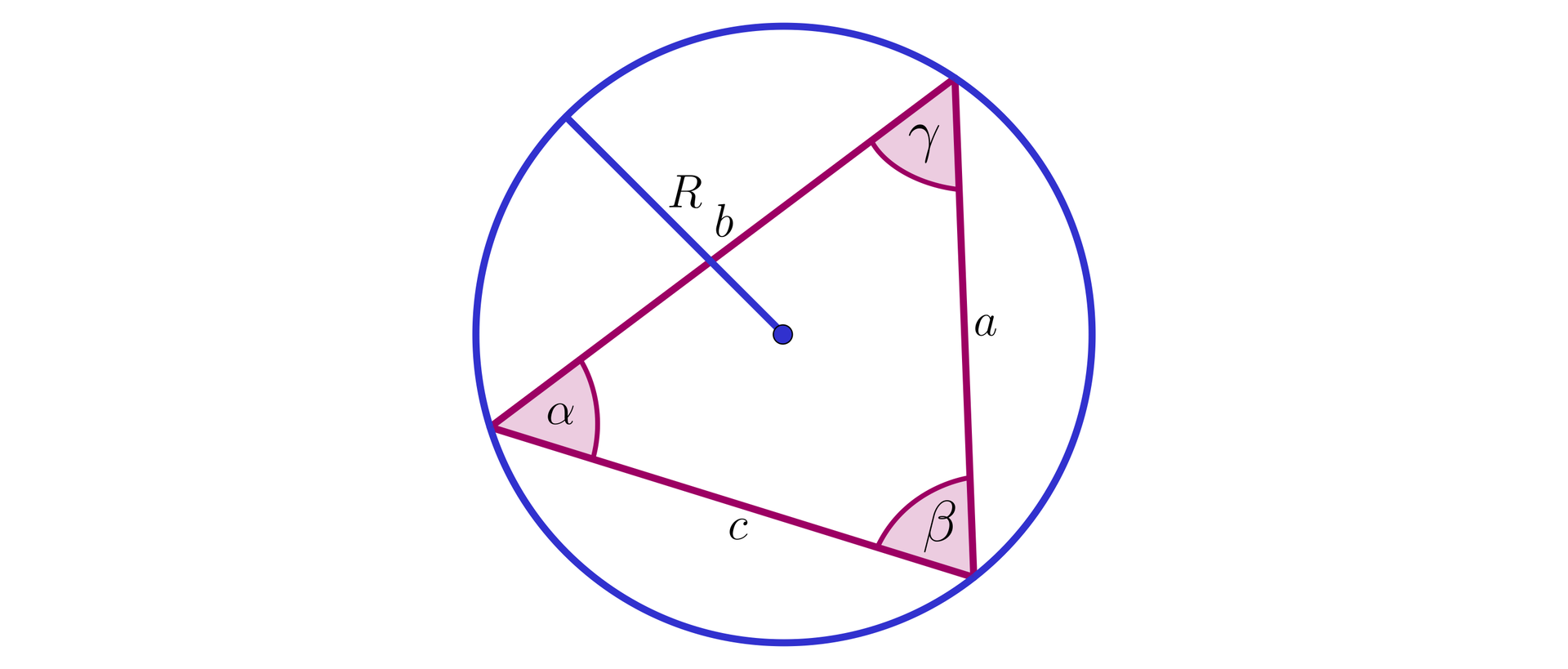
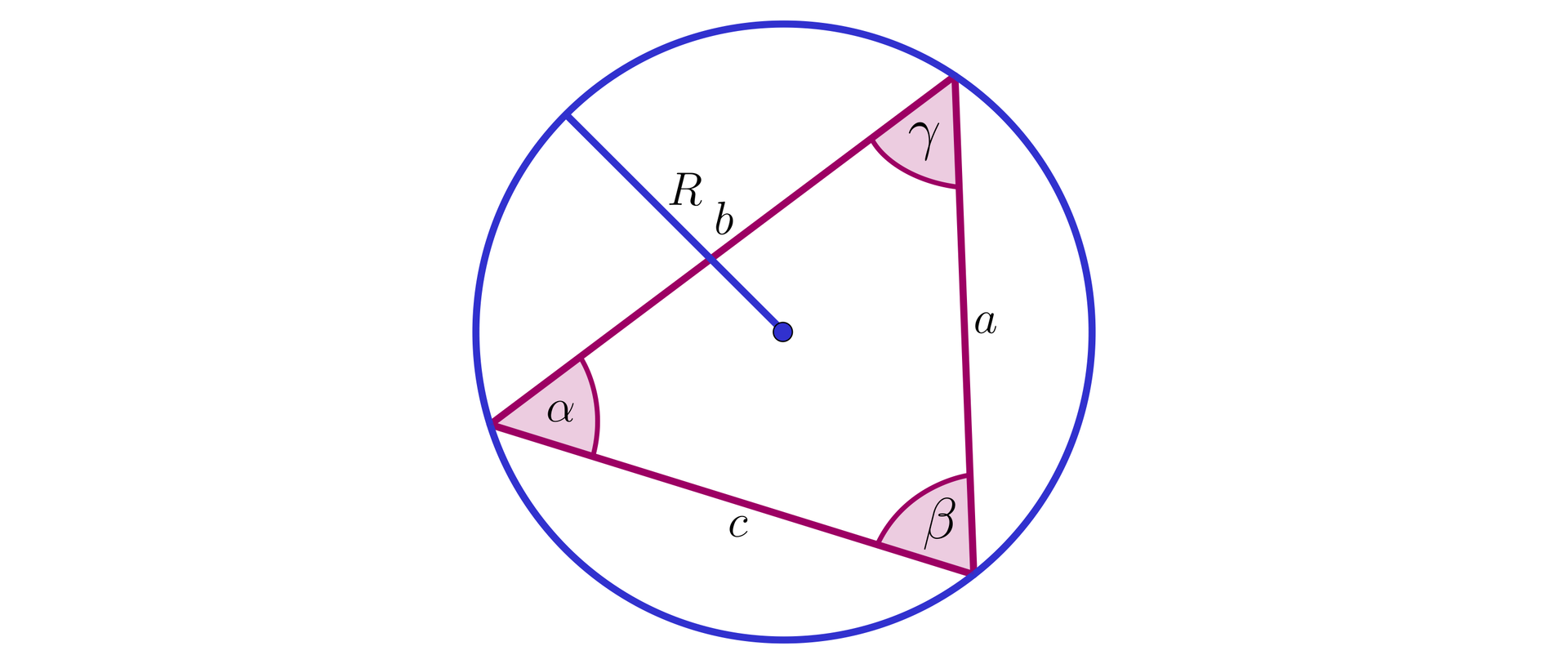
Zaznacz poprawną odpowiedź. Jeżeli $R$ jest długością promienia okręgu opisanego na trójkącie o polu $P$ , w którym kąty wewnętrzne mają miary $α$ , $β$ , $γ$ , to:

$R = \sqrt{\frac{P}{2 \sin α \cdot \sin β \cdot \sin γ}}$
$R = \sqrt{\frac{2 \sin α \cdot \sin β \cdot \sin γ}{P}}$
$R = 2 \sqrt{\frac{P}{\sin α \cdot \sin β \cdot \sin γ}}$

Ćwiczenie 2

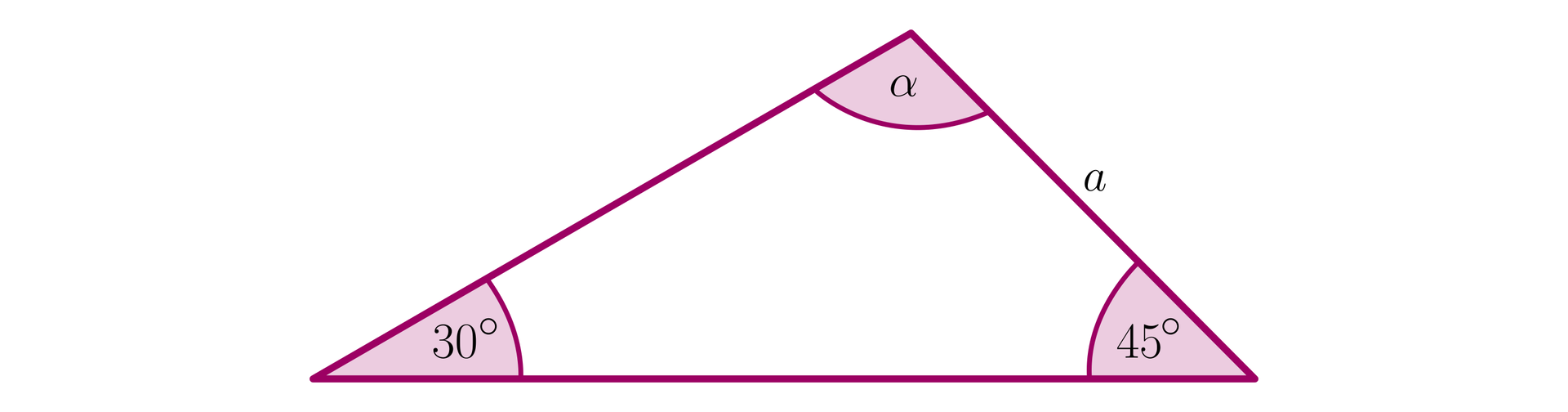
Na podstawie rysunku zaznacz zdania, które są prawdziwe.

R1eA603lcYA11

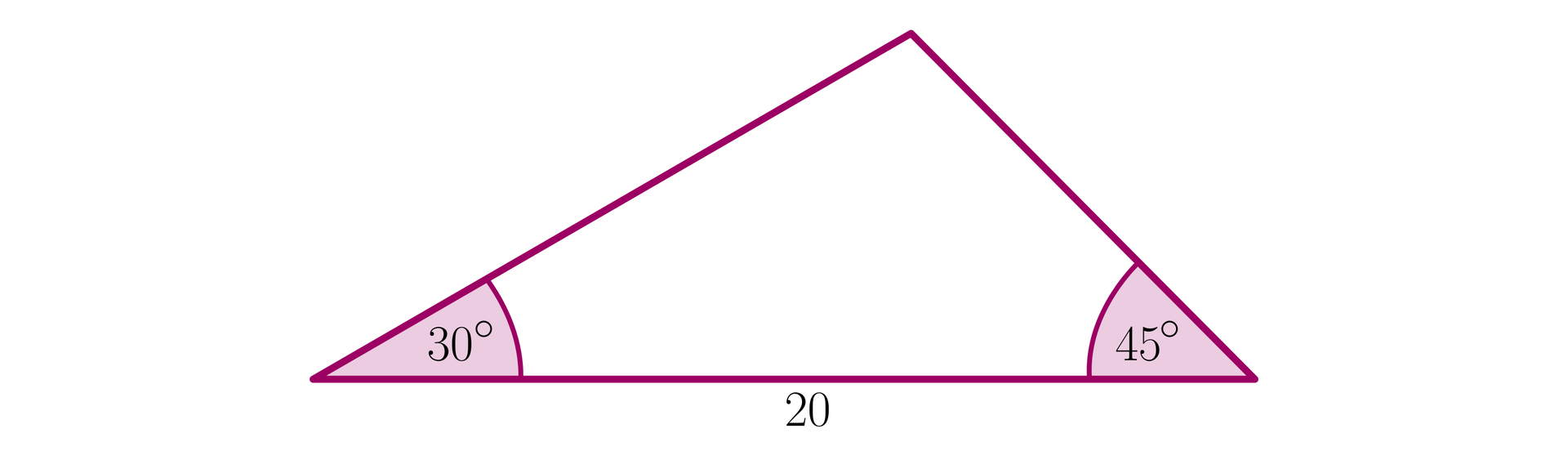
Ilustracja przedstawia trójkąt z zaznaczonymi kątami trzydziestu stopni oraz czterdziestu stopni przy podstawie trójkąta, która ma długość dwadzieścia.

R10BrXzDP8RNj

Długość promienia okręgu opisanego na tym trójkącie wynosi $10 \sqrt{6} - 10 \sqrt{2}$ .
Długość promienia okręgu opisanego na tym trójkącie wynosi $40$ .
Pole trójkąta z rysunku jest równe $70 \sqrt{2}$ .
Pole trójkąta z rysunku jest równe $100 \sqrt{3} - 100$ .

Ćwiczenie 3

Re6GRVmnu3zid

Wstaw w tekst odpowiednie liczby lub tekst. Dany jest trójkąt o boku

c = 4

oraz kątach

α = 30 °

β = 45 °

.
Długość boku

a

jest równa długości 1.

2 \sqrt{6} - 2 \sqrt{2}

, 2. promienia okręgu opisanego na tym trójkącie, 3. średnicy okręgu opisanego na tym trójkącie., 4.

4 \sqrt{6} - 4 \sqrt{2}

, 5.

4 \sqrt{3} - 4

.
Pole tego trójkąta jest równe 1.

2 \sqrt{6} - 2 \sqrt{2}

, 2. promienia okręgu opisanego na tym trójkącie, 3. średnicy okręgu opisanego na tym trójkącie., 4.

4 \sqrt{6} - 4 \sqrt{2}

, 5.

4 \sqrt{3} - 4

.
Długość promienia okręgu opisanego na tym trójkącie jest równa 1.

2 \sqrt{6} - 2 \sqrt{2}

, 2. promienia okręgu opisanego na tym trójkącie, 3. średnicy okręgu opisanego na tym trójkącie., 4.

4 \sqrt{6} - 4 \sqrt{2}

, 5.

4 \sqrt{3} - 4

Wstaw w tekst odpowiednie liczby lub tekst.

$4 \sqrt{3} - 4$ , $2 \sqrt{6} - 2 \sqrt{2}$ , średnicy okręgu opisanego na tym trójkącie, $4 \sqrt{6} - 4 \sqrt{2}$ , promienia okręgu opisanego na tym trójkącie

Dany jest trójkąt o boku $c = 4$ oraz kątach $α = 30 °$ , $β = 45 °$ .
Długość boku $a$ jest równa długości .............................................................................................
Pole tego trójkąta jest równe .............................................................................................
Długość promienia okręgu opisanego na tym trójkącie jest równa .............................................................................................

Ćwiczenie 4

RNWdpQupi1kWP

R1FuhLVXf92Uq

Ćwiczenie 5

Wykaż, że jeżeli $R$ jest długością promienia okręgu opisanego na trójkącie o bokach $a$ , $b$ , $c$ i kątach $α$ , $β$ , $γ$ , to długość promienia wyraża się wzorem $R = \frac{1}{2} \cdot \sqrt[3]{\frac{a b c}{\sin α \cdot \sin β \cdot \sin γ}}$

Narysujmy rysunek pomocniczy i wprowadźmy oznaczenia, jak na rysunku.

RtEeGmO0K0qvz

Ilustracja przedstawia trójkąt wpisany w okrąg. Boki trójkąta podpisano literami a b oraz c. Kąt pomiędzy bokami a i c podpisano literą beta. Kąt pomiędzy a i b podpisano literą gamma. Kąt pomiędzy b i c podpisano literą alfa. Ze środka okręgu poprowadzono promień, który podpisano literą R.

Korzystając z twierdzenia sinusów pole trójkąta, możemy obliczyć za pomocą wzorów:

$P = 2 R^{2} \cdot \sin α \cdot \sin β \cdot \sin γ$

$P = \frac{a b c}{4 R}$

Jeżeli porównamy te wielkości, to otrzymujemy zależność:

$\frac{a b c}{4 R} = 2 R^{2} \cdot \sin α \cdot \sin β \cdot \sin γ$

Równanie przekształcamy do postaci:

$a b c = 8 R^{3} \cdot \sin α \cdot \sin β \cdot \sin γ$

$R^{3} = \frac{a b c}{8 \sin α \cdot \sin β \cdot \sin γ}$

Wobec tego

$R = \frac{1}{2} \cdot \sqrt[3]{\frac{a b c}{\sin α \cdot \sin β \cdot \sin γ}}$

Ćwiczenie 6

Oblicz pole trójkąta, w którym najkrótszy bok ma długość $6$ , a dwa kąty tego trójkąta mają miary $30 °$ i $45 °$ .

Narysujmy trójkąt i wprowadźmy oznaczenia, jak na poniższym rysunku.

R9ApupxuK8ujC

Ilustracja przedstawia trójkąt z zaznaczonymi trzema kątami. Kąt trzydziestu stopni oraz czterdziestu stopni znajduje się przy podstawie trójkąta, natomiast kąt alfa został utworzony pomiędzy dwoma ramionami figury. Jedno z ramion ma długość a.

Z warunków zadania wynika, że $a = 6$ oraz $α = 180 ° - (30 ° + 45 °) = 105 °$ .

W celu wyznaczenia wielkości $\sin 105 °$ użyjemy wzoru na sinus sumy kątów.

Zatem

$\sin 105 ° = \sin (60 ° + 45 °) = \sin 60 ° \cdot \cos 45 ° + \sin 45 ° \cdot \cos 60 ° =$

$= \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} \cdot \frac{1}{2} = \frac{\sqrt{6}}{4} + \frac{\sqrt{2}}{4} = \frac{\sqrt{6} + \sqrt{2}}{4}$

Wobec tego pole trójkąta wynosi:

$P = \frac{1}{2} \cdot 6^{2} \cdot \frac{\sin 105 ° \cdot \sin 45 °}{\sin 30 °} = 18 \cdot \frac{\frac{\sqrt{6} + \sqrt{2}}{4} \cdot \frac{\sqrt{2}}{2}}{\frac{1}{2}} =$

$= \frac{9 \cdot (2 + \sqrt{12})}{2} = 9 + 9 \sqrt{3}$

Ćwiczenie 7

Wykaż, że jeśli boki trójkąta mają długości $a$ , $b$ , $c$ , a kąty odpowiednio $α$ , $β$ , $γ$ , to pole trójkąta możemy obliczyć za pomocą wzoru $P = \frac{c^{2}}{2} \cdot \frac{\sin α \cdot \sin β}{\sin (α + β)}$ dla $α \neq β \neq 90 °$ .

Do rozwiązania zadania wykorzystamy wzór na pole trójkąta postaci:

$P = \frac{c^{2}}{2} \cdot \frac{tg α \cdot tg β}{tg α + tg β}$

oraz wzór na sinus sumy kątów:

$\sin (α + β) = \sin α \cdot \cos β + \sin β \cdot \cos α$

Zatem:

$P = \frac{c^{2}}{2} \cdot \frac{tg α \cdot tg β}{tg α + tg β} = \frac{c^{2}}{2} \cdot \frac{\frac{\sin α}{\cos α} \cdot \frac{\sin β}{\cos β}}{\frac{\sin α}{\cos α} + \frac{\sin β}{\cos β}} =$

$= \frac{c^{2}}{2} \cdot \frac{\frac{\sin α \cdot \sin β}{\cos α \cdot \cos β}}{\frac{\sin α \cdot \cos β + \sin β \cdot \cos α}{\cos α \cdot \cos β}} = \frac{c^{2}}{2} \cdot \frac{\sin α \cdot \sin β}{\sin α \cdot \cos β + \sin β \cdot \cos α}$

$= \frac{c^{2}}{2} \cdot \frac{\sin α \cdot \sin β}{\sin (α + β)}$

Ćwiczenie 8

Oblicz pole trójkąta, w którym promień okręgu na nim opisanego ma długość $R = 18$ oraz dane są miary dwóch kątów wewnętrznych tego trójkąta $α = 45 °$ i $β = 15 °$ .

Narysujmy trójkąt i wprowadźmy oznaczenia, jak na poniższym rysunku.

RTqhUzPc4eLKu

Z treści zadania wynika, że $α = 45 °$ i $β = 15 °$ .

Zatem $γ = 180 ° - (45 ° + 15 °) = 120 °$ .

Do obliczenia wartości pola wykorzystamy wzór $P = 2 R^{2} \cdot \sin α \cdot \sin β \cdot \sin γ$

Zauważmy, że:

$\sin 120 ° = \sin 60 ° = \frac{\sqrt{3}}{2}$

$\sin 15 ° = \sin (60 ° - 45 °) = \sin 60 ° \cdot \cos 45 ° - \sin 45 ° \cdot \cos 60 ° =$

$= \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} \cdot \frac{1}{2} = \frac{\sqrt{6} - \sqrt{2}}{4}$

Zatem pole tego trójkąta jest równe:

$P = 2 \cdot 18^{2} \cdot \sin 45 ° \cdot \sin 15 ° \cdot \sin 120 ° =$

$= 2 \cdot 324 \cdot \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{6} - \sqrt{2}}{4} \cdot \frac{\sqrt{3}}{2} = 243 - 81 \sqrt{3}$

Animacja

Dla nauczyciela