Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Przez dwa wierzchołki sześcianu poprowadzono prostą $l$ . Ile jest prostych równoległych do $l$ , do których należy przynajmniej jeden wierzchołek sześcianu, jeżeli

R1XHTzQr3X9mn

$l$ zawiera krawędź sześcianu:

R9cT8vzXrN9kS

$l$ zawiera przekątną ściany bocznej:

RyNb8XzAitUOK

$l$ zawiera główną przekątną sześcianu:

R1XHTzQr3X9mn

$l$ zawiera krawędź sześcianu:

R9cT8vzXrN9kS

$l$ zawiera przekątną ściany bocznej:

RyNb8XzAitUOK

$l$ zawiera główną przekątną sześcianu:

Ćwiczenie 2

Przez dwa wierzchołki sześcianu poprowadzono prostą $l$ . Ile jest prostych równoległych do $l$ , do których należą dwa wierzchołki sześcianu, jeżeli

RJiX452PL2M88

$l$ zawiera krawędź sześcianu:

R10fhAB1BfPkf

$l$ zawiera przekątną ściany bocznej:

R16u1icOSXFjl

$l$ zawiera główną przekątną sześcianu:

RJiX452PL2M88

$l$ zawiera krawędź sześcianu:

R10fhAB1BfPkf

$l$ zawiera przekątną ściany bocznej:

R16u1icOSXFjl

$l$ zawiera główną przekątną sześcianu:

Ćwiczenie 3

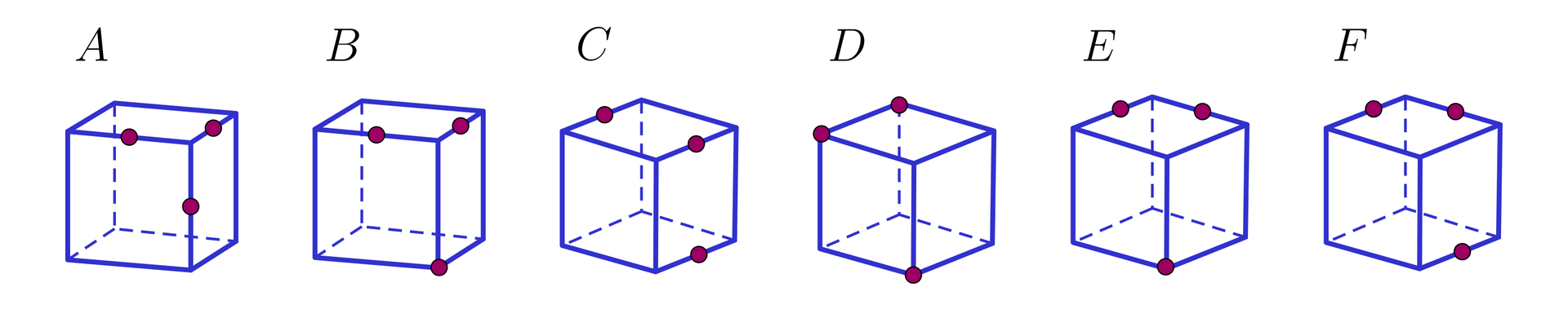
Na każdym z sześcianów zaznaczono na czerwono trzy punkty, przez które poprowadzono płaszczyznę. Podane wielokąty przedstawiają przekroje podanych sześcianów wybranymi płaszczyznami. Dopasuj przekrój do sześcianu i zaznaczonych na nim punktów.

RtCwyBSwAbaGu

Ilustracja przedstawia sześć sześcianów podpisanych literami A B C D E F. Pierwszy z nich jest podpisany literą A, na dwóch sąsiadujących krawędziach jego górnej podstawy oraz na krawędzi bocznej pomiędzy tymi krawędziami podstaw zaznaczono punkty. W drugim sześcianie, podpisanym literą B, na dwóch sąsiadujących krawędziach jego górnej podstawy oraz na wierzchołku dolnej podstawy znajdującym się pomiędzy tymi krawędziami podstaw zaznaczono punkty. W trzecim sześcianie, który podpisano literą C również zaznaczono trzy punkty, dwa z nich lezą na przeciwległych krawędziach górnej podstawy, a trzeci leży na bezpośrednio pod jednym z punktów z tym, że na krawędzi dolnej podstawy. W czwartym sześcianie podpisanym literą D zaznaczono punkty w dwóch sąsiadujących wierzchołkach górnej podstawy oraz naprzeciwległym wierzchołku dolnej podstawy. W sześcianie podpisanym literą E na dwóch sąsiadujących krawędziach jego górnej podstawy zaznaczono punkty, a trzeci punkt zaznaczono w wierzchołku dolnej podstawy, który leży naprzeciw wierzchołka znajdującego się pomiędzy krawędziami z punktami. W sześcianie podpisanym literą F punkty zaznaczono w następujący sposób: dwa punkty zaznaczono na dwóch sąsiadujących krawędziach jego górnej podstawy, a trzeci na krawędzi dolnej podstawy leżącej naprzeciw jednego z punktów górnej podstawy.

RL5nmWykranWZ

R1ATC9H7SmAGm

RVTObLnV8YBkC2

Ćwiczenie 4

Ocen prawdziwość poniższych zdań

	Prawda	Fałsz
Różne proste równoległe nie mają punktów wspólnych.	□	□
Jeżeli proste w przestrzeni nie mają punktów wspólnych to są równoległe.	□	□
Proste równoległe do trzeciej prostej są równoległe do siebie.	□	□
Jeżeli proste mają dwa punkty wspólne to są równoległe.	□	□
Wszystkie proste równoległe do danej prostej leżą w jednej płaszczyźnie.	□	□
Każda prosta równoległa do danej prostej leży w tej samej płaszczyźnie co dana prosta.	□	□

Ćwiczenie 5

Wykaż, że jeśli dwie różne proste $l$ , $l'$ są równoległe do trzeciej prostej, to nie mają punktów wspólnych.

Ćwiczenie 6

Wykaż, że jeśli różne proste $l$ , $l'$ są równoległe, to dowolna płaszczyzna zawierająca $l$ i różna od wspólnej płaszczyzny prostych $l$ , $l'$ nie ma punktów wspólnych z $l'$ .

Załóżmy, że płaszczyzna $π$ zawiera prostą $l$ . Gdyby prosta $l'$ miała punkt wspólny z $π$ to przez ten punkt można poprowadzić dokładnie jedną prostą równoległą do $l$ , czyli prostą $l'$ . Stąd płaszczyzna $π$ jest płaszczyzną wspólną obu prostych.

Ćwiczenie 7

Niech $l$ będzie dowolną prostą, która przebija płaszczyznę $π$ w punkcie $A$ . Wykaż, że pęk prostych równoległych do $l$ wyznaczony przez punkty płaszczyzny $π$ tworzy całą przestrzeń.

Niech $B$ będzie dowolnym punktem przestrzeni. Prowadzimy prostą $k$ równoległą do $l$ przechodzącą przez punkt $B$ . Z własności prostej równoległej do prostej przebijającej płaszczyznę wynika, że prosta $k$ przebija płaszczyznę $π$ . Stąd $k$ należy do pęku prostych równoległych do $l$ wyznaczonego przez punkty płaszczyzny $π$ .

Ćwiczenie 8

Z belki o ośmiu krawędziach, z których każde dwie sąsiednie są równoległe wycięto pochylony graniastosłup w taki sposób, że podstawy $A B C D E F G H$ i $A' B' C' D' E' F' G' H'$ są ośmiokątami foremnymi, a ściany boczne są równoległobokami.

RYNcfuifVAG8U

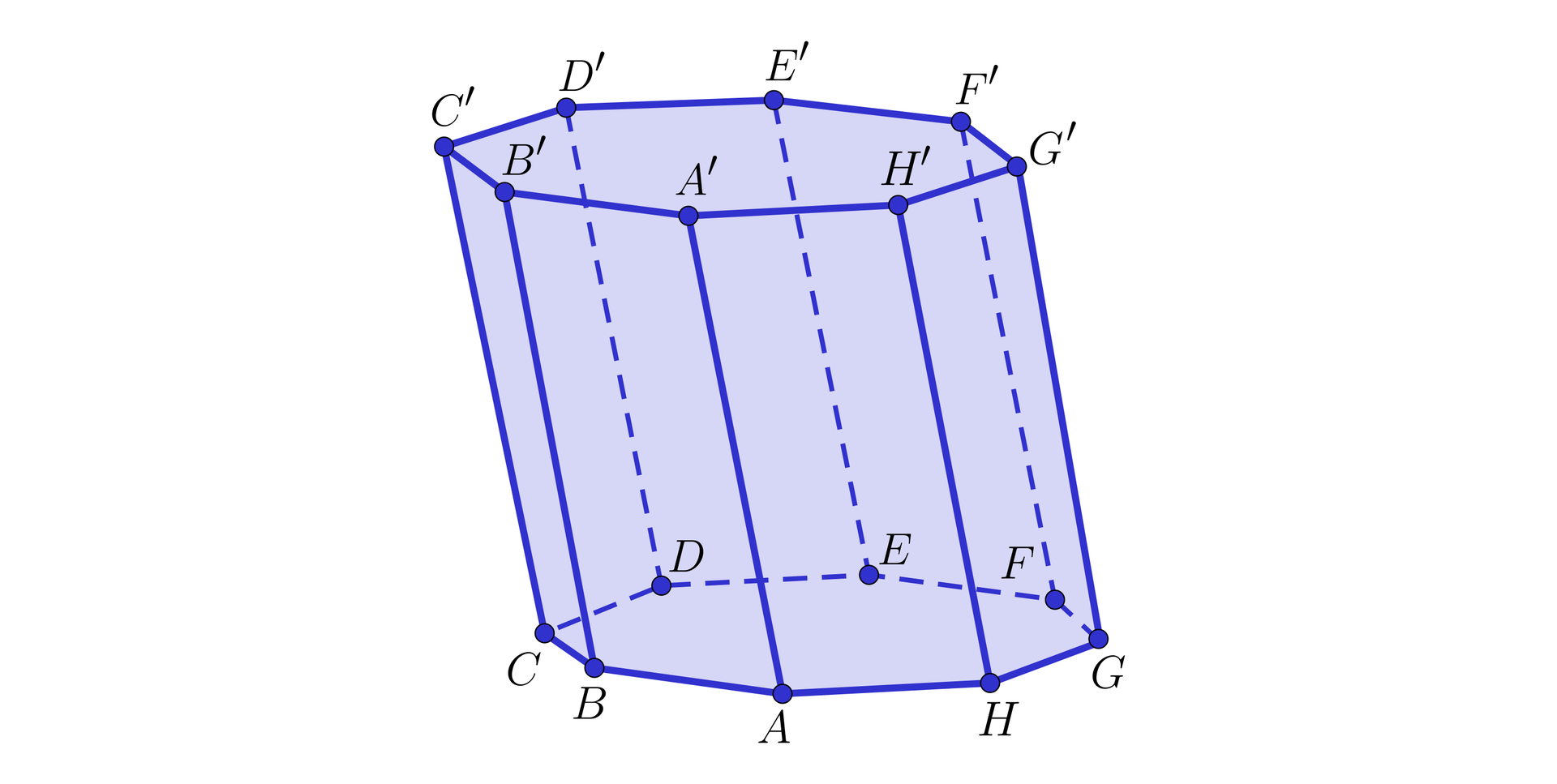
Ilustracja przedstawia graniastosłup pochylony o podstawie ośmiokąta. Wierzchołki dolnej podstawy to: A B C D E F H G. Wierzchołki górnej podstawy to: A' B' C' D' E' F' G' H'.

Czy można jednym cięciem przejść przez dane $4$ punkty? Odpowiedź uzasadnij.

1. Dane $4$ punkty, to $A$ , $A'$ , $E'$ , $E$

2. Dane $4$ punkty, to $A$ , $B'$ , $C'$ , $D$

3. Dane $4$ punkty, to $A$ , $B'$ , $D'$ , $C$

1. Tak. Ponieważ sąsiednie krawędzie są równoległe, to $A A^{'} ∥ B B^{'} ∥ C C^{'} ∥ D D^{'} ∥ E E^{'}$ . Zatem proste $A A'$ , $E E'$ leżą w jednej płaszczyźnie. A skoro leżą w jednej płaszczyźnie, to można dokonać cięcia.

2. Tak. Ponieważ $A D ∥ B C ∥ B' C'$ , to proste $A D$ , $B' C'$ leżą w jednej płaszczyźnie. A skoro leżą w jednej płaszczyźnie, to można dokonać cięcia.

3. Nie. Ponieważ $B' D' ∥ B D ∥ A E$ , to punkty $A$ , $B'$ , $D'$ , $E$ leżą w płaszczyźnie wyznaczonej przez punkty $A$ , $E$ , $B'$ . Punkt $D$ do niej nie należy, gdyż leży na prostej $B D$ , która jest równoległa do $A E$ i wspólnie wyznaczają płaszczyznę podstawy, która w przecięciu z płaszczyzną $A E B'$ daje prostą $A E$ .

Animacja 3D

Dla nauczyciela