Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

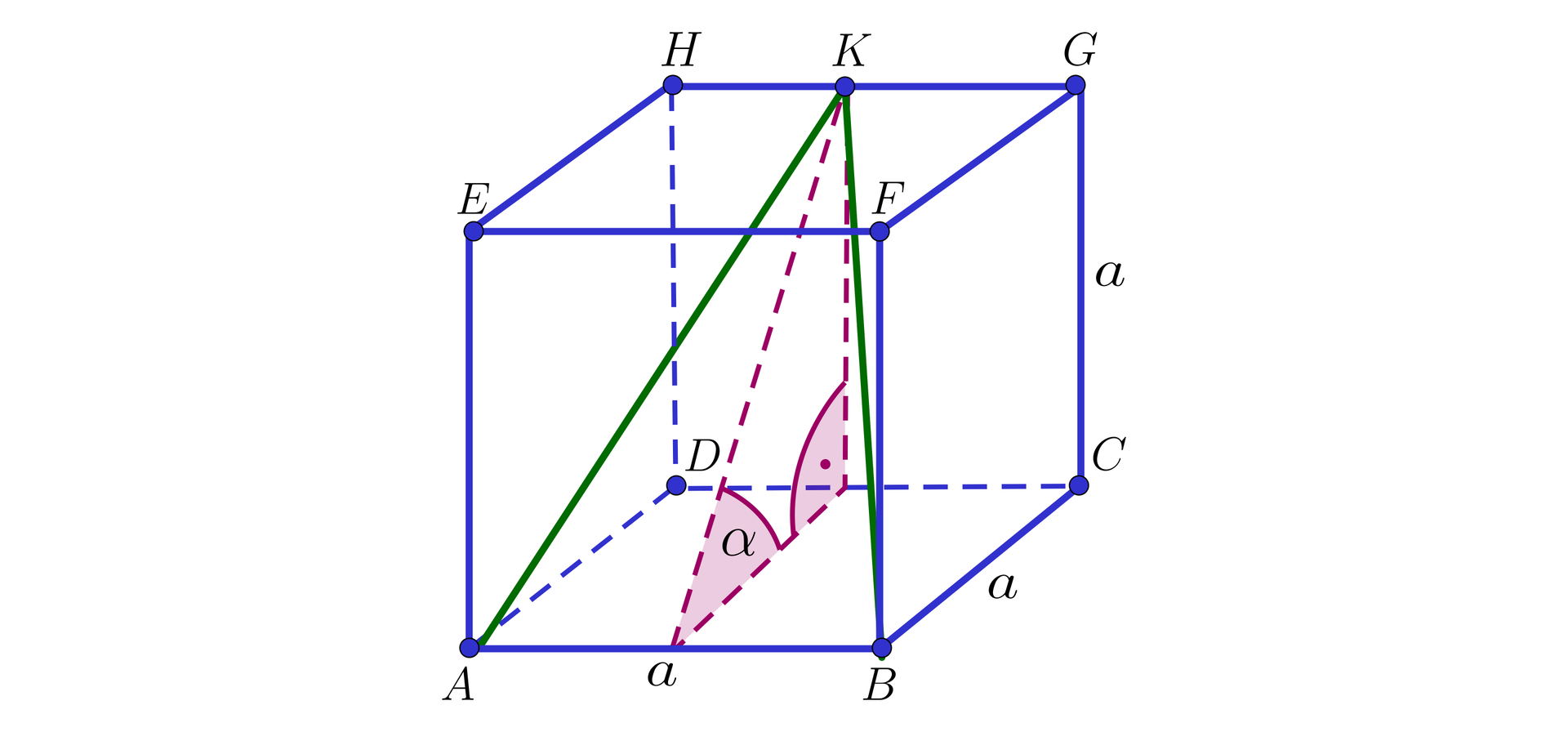
Na rysunku przedstawiono sześcian $A B C D E F G H$ oraz zaznaczono kąt dwuścienny $α$ .

Rpxnui6PWo6zo

Ilustracja przedstawia sześcian A B C D E F G H. W połowie krawędzi bocznych A D i B C poprowadzono odcinek K L , równoległy do odcinka A B. Punkt K połączono z wierzchołkiem H, natomiast punkt L z wierzchołkiem G tworząc tym samym nową płaszczyznę wewnątrz sześcianu. Na ilustracji zaznaczony został także kąt alfa przy punkcie L, opisujący nachylenie płaszczyzny do podstawy A B C D.

RTvaTgSQjPwlm

Zaznacz poprawną odpowiedź.

Ścianami kąta dwuściennego $α$ są półpłaszczyzny $K L C D$ oraz $K L G H$ .
Ścianami kąta dwuściennego $α$ są półpłaszczyzny $K L C D$ oraz $C G H D$ .
Krawędzią zaznaczonego kąta dwuściennego jest odcinek $A B$ .

Ćwiczenie 2

Na rysunku przedstawiono graniastosłup trójkątny $A B C D E F$ .

RbtccCykLLUME

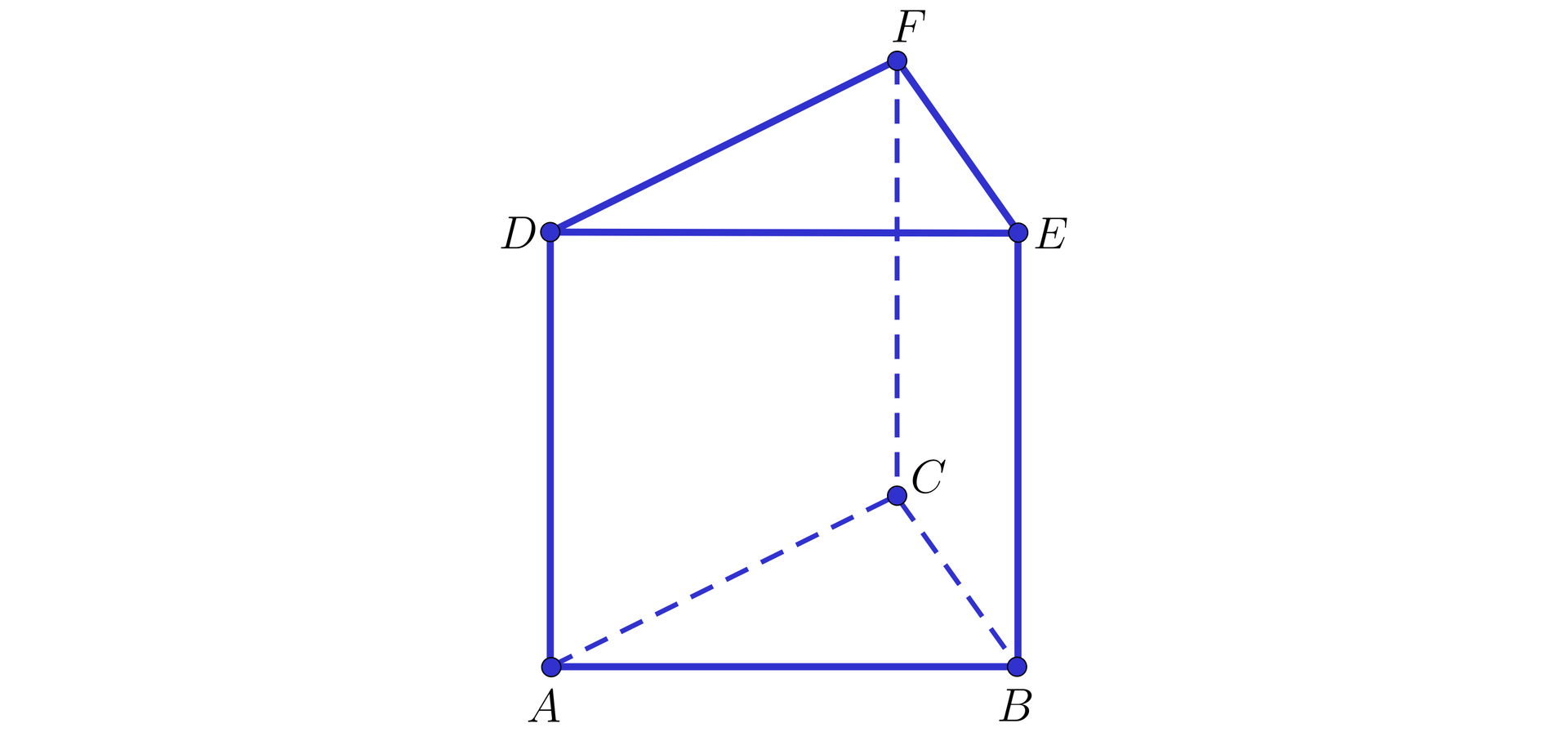
Ilustracja przedstawia graniastosłup trójkątny A B C D E F. W podstawie dolnej znajduje się trójkąt A B C, natomiast w podstawie górnej znajduje się trójkąt D E F.

RGXfsvZZTLV3Q

Zaznacz wszystkie zdania, które są prawdziwe.

Jeżeli jedną ścianą kąta dwuściennego jest ściana $A B C$ , to drugą ścianą może być dowolna półpłaszczyzna zawierająca ścianę boczną graniastosłupa.
Jeżeli jedną ścianą kąta jest półpłaszczyzna $A B C$ , to drugą ścianą kąta dwuściennego może być półpłaszczyzna $D E F$ .
Dowolna półpłaszczyzna, zawierająca ścianę boczną graniastosłupa z rysunku tworzy $3$ kąty dwuścienne z sąsiednimi ścianami.
Istnieje dokładnie $18$ kątów dwuściennych, które tworzą półpłaszczyzny zawierające ściany graniastosłupa.

REyZVzjjyKvfQ1

Ćwiczenie 3

Uzupełnij tekst dotyczący kąta dwuściennego.

ściany, krawędź, krawędzi, Wnętrze, figura geometryczna, kąt dwuścienny, półpłaszczyzny, obszar

Kąt dwuścienny jest to ...................................... utworzona przez dwie różne ...................................... o wspólnej ...................................... i jedną z dwóch figur wyciętych w przestrzeni przez te dwie półpłaszczyzny.
Dwie półpłaszczyzny wyznaczające ...................................... to ...................................... tego kąta, natomiast część wspólna obu płaszczyzn to ...................................... kąta dwuściennego. ...................................... kąta dwuściennego to figura wycięta z przestrzeni przez ściany kąta dwuściennego. Suma ścian i wnętrza kąta dwuściennego, to jego .......................................

Ćwiczenie 4

R1CNP0jXMh16K

R1Z74EPNUrRQg

fhfh

RLgK3vet8xrpb2

Ćwiczenie 5

Rozwiąż krzyżówkę.

Rodzaj kąta, który tworzą dwie półpłaszczyzny o wspólnej krawędzi.
Jest nią ściana kąta dwuściennego.
Najczęściej podawana w stopniach lub radianach dla kąta.
Wspólna dla dwóch półpłaszczyzn.
Figura wycięta z przestrzeni przez ściany kąta dwuściennego.
Suma ścian i wnętrza kąta dwuściennego.

1
2
3
4
5
6

Ćwiczenie 6

Narysuj sześcian $A B C D E F G H$ i zaznacz:

kąt pomiędzy płaszczyzną $A B K$ , gdzie $K$ jest środkiem krawędzi $G H$ , a płaszczyzną podstawy $A B C D$ tego sześcianu,
kąt pomiędzy płaszczyzną $A B H$ , a płaszczyzną podstawy $A B C D$ tego sześcianu.

Niech $α$ będzie szukanym kątem. Wówczas rysunek przedstawia się następująco:
R1AYVDTp3Jc54
Ilustracja przedstawia sześcian A B C D E F G H o długości krawędzi a. Z punktu A oraz B poprowadzono dwa odcinki ograniczone punktem K, znajdującym się w środku krawędzi górnej podstawy H G. Z punktu K natomiast poprowadzono półprostą przechodzącą przez środek odcinka A B. W miejscu przecięcia się półprostej z odcinkiem A B znajduje się kąt alfa opisujący kąt nachylenia półprostej wychodzącej z punktu K względem powierzchni podstawy A B C D.
Niech $α$ będzie szukanym kątem. Wówczas rysunek przedstawia się następująco:
RjwRgJqvhqZGP

Zauważmy, że w obu przypadkach jest mowa o tym samym kącie dwuściennym.

R1AYdF466iROy3

Ćwiczenie 7

Zaznacz poprawną odpowiedź. Dany jest czworościan foremny $A B C D$ . Wówczas:

Miary kątów między ścianami tego czworościanu nie zależą od wyboru ścian.
Istnieje jedna płaszczyzna, zawierająca ścianę czworościanu, która nie tworzy kąta dwuściennego z żadną z pozostałych płaszczyzn, zawierających ściany tego czworościanu.
Krawędzią wspólną płaszczyzn $A B C$ i $B D C$ jest odcinek $A D$ .

RgOrZKnWCUMmL3

Ćwiczenie 8

Uporządkuj w odpowiedniej kolejności etapy wyznaczenia kąta dwuściennego pomiędzy ścianami bocznymi w ostrosłupie prawidłowym sześciokątnym.

Na wybranych ścianach bocznych wykreślamy odcinki, które są prostopadłe do wyróżnionej krawędzi bocznej.
Narysowane odcinki są wysokościami trójkątów będących ścianami bocznymi ostrosłupa.
Wyznaczamy krawędź wspólną sąsiednich ścian bocznych.
Kąt pomiędzy wysokościami ścian bocznych jest kątem dwuściennym.

Aplet

Dla nauczyciela