Średnia arytmetyczna zestawu danych
Analizując przykłady zawarte w tym materiale dowiesz się, jak obliczyć średnią arytmetyczną zestawu danych, również w sytuacji praktycznej.
Aby obliczyć średnią arytmetyczną zestawu danych, należy je do siebie dodać i otrzymaną sumę podzielić przez ich liczbę.
Poniższe animacje pokazują jak obliczyć średnią ocen ze sprawdzianu z matematyki w pewnej klasie.
Film dostępny pod adresem /preview/resource/RbZHTZmSv06lC
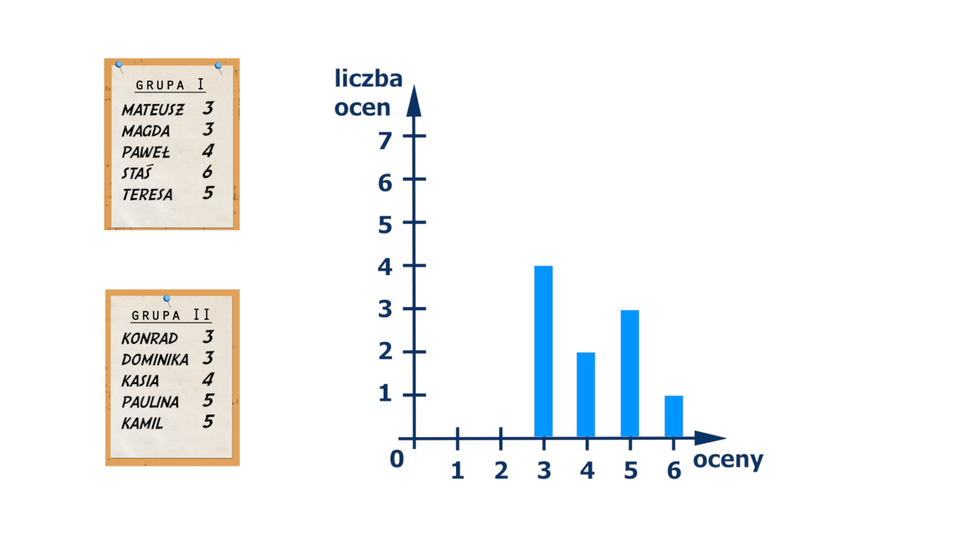
Animacja przedstawia w jaki sposób możemy obliczyć średnią arytmetyczną ocen ze sprawdzianu dla każdej z dwóch grup uczniów.

Film dostępny pod adresem /preview/resource/R12tncEsm8sXE
Animacja przedstawia w jaki sposób możemy obliczyć średnią arytmetyczną ocen ze sprawdzianu dla każdej z trzech grup uczniów.

Film dostępny pod adresem /preview/resource/RVCCHs3glNTJA
Animacja przedstawia w jaki sposób możemy obliczyć średnią arytmetyczną ocen ze sprawdzianu dla każdej z dwóch grup uczniów.
Poniższe animacje pokazują jak obliczyć średnią ocen ze sprawdzianu z matematyki w pewnej klasie.

Film dostępny pod adresem /preview/resource/RS1ykcHUPebbo
Animacja przedstawia w jaki sposób możemy obliczyć średnią arytmetyczną ocen ze sprawdzianu dla każdej z dwóch grup uczniów.

Film dostępny pod adresem /preview/resource/Rdng5L8Q36nVg
Animacja przedstawia w jaki sposób możemy obliczyć średnią arytmetyczną ocen ze sprawdzianu dla każdej z dwóch grup uczniów oraz średnią arytmetyczną ocen ze sprawdzianu dla wszystkich uczniów z obu grup.
Poniższa animacja pokazuje jak obliczyć średnią ocen ze sprawdzianu z matematyki w pewnej klasie.

Film dostępny pod adresem /preview/resource/REA6XoF6rLz0j
Animacja przedstawia w jaki sposób możemy obliczyć średnią arytmetyczną ocen ze sprawdzianu dla każdej z dwóch grup uczniów oraz średnią arytmetyczną ocen ze sprawdzianu dla wszystkich uczniów z obu grup.
Poniższa animacja pokazuje jak obliczyć średnią ocen ze sprawdzianu z matematyki w pewnej klasie.

Film dostępny pod adresem /preview/resource/RyTPfVouyrZSA
Animacja przedstawia w jaki sposób możemy obliczyć średnią arytmetyczną ocen ze sprawdzianu dla każdej z dwóch grup uczniów oraz średnią arytmetyczną ocen ze sprawdzianu dla wszystkich uczniów z obu grup.
- Średnia wyrazów: piątego i szóstego
- Wyraz piąty
- Wyraz szósty
- Średnia wyrazów: czwartego, piątego i szóstego
- Jeżeli jeden z pięciu wyrazów zestawu danych zwiększymy o , drugi zwiększymy o , trzeci i czwarty pozostawimy bez zmian, a piąty zmniejszymy o , to średnia arytmetyczna tego zestawu nie zmieni się.
- Jeżeli zawartość jednego z czterech naczyń, w których znajduje się jednakowa ilość płynu, rozlejemy do trzech pozostałych, to średnia arytmetyczna ilości płynu w naczyniach zmieni się.
- Jeżeli płacę pani Kowalskiej zwiększymy o , a płacę pana Kowalskiego zmniejszymy o , to średnia płaca państwa Kowalskich nie ulegnie zmianie.
- Jeżeli średni wiek rodziny Tomka składającej się z rodziców, Tomka i dwójki rodzeństwa Tomka wynosi lat, to średnia wieku rodziny Tomka wraz z mającą lat babcią będzie większa niż lat.
W tabeli przedstawionych zostało sześć zestawów danych uporządkowanych rosnąco.
Nr | Zestaw danych |
|---|---|
, , , , , , , , , , , , , , | |
, , , , , , , , , , , , , , , , , | |
, , , , , , , , , , , , , | |
, , , , , , , , , , , , | |
, , , , , , , , , , , , , | |
, , , , , , , , , , , |
Oblicz średnią arytmetyczną ocen uzyskanych przez uczniów tej klasy. Uzupełnij poniższe luki. Kliknij w nie, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. Odpowiedź: Średnia arytmetyczna uczniów tej klasy wynosi: 1. , 2. , 3. , 4. .
Wyznacz średnią arytmetyczną liczby punktów uzyskanych z egzaminu przez uczniów każdej z klas oraz grupy składającej się ze wszystkich uczniów obu klas. Uzupełnij poniższe luki. Kliknij w nie, aby rozwinąć listę, a następnie wybierz poprawną liczbę w każdym przypadku. Średnia arytmetyczna uczniów z klasy Krysi wynosi 1. , 2. , 3. , 4. , 5. , 6. .Średnia arytmetyczna uczniów z klasy Zuzi wynosi 1. , 2. , 3. , 4. , 5. , 6. .Średnia arytmetyczna uczniów z obu klas wynosi 1. , 2. , 3. , 4. , 5. , 6. .
W tabeli podano liczby książek znajdujących się na półkach w szkolnej bibliotece.
Liczba książek na półce | Liczba półek |
|---|---|
Zapytano uczniów dwóch klas pierwszych, ile książek czytają w ciągu miesiąca. Otrzymane odpowiedzi umieszczono w tabelach:
Klasa
Liczba książek | Liczba uczniów |
|---|---|
Klasa
Liczba książek | Liczba uczniów |
|---|---|
Oblicz średnią arytmetyczną liczby książek czytanych w ciągu miesiąca:
dla każdej z klas,
dla grupy złożonej z uczniów obu klas.
Wykres przedstawia wyniki biegu, który odbył się w czasie szkolnych zawodów.

Połącz w pary zestawy liczb z pojedynczymi liczbami tak, aby średnia arytmetyczna nowego zestawu wyniosła .
<span aria-label="dwa" role="math"><math><mn>2</mn></math></span>, <span aria-label="cztery" role="math"><math><mn>4</mn></math></span>, <span aria-label="dziewięć" role="math"><math><mn>9</mn></math></span>, <span aria-label="jeden" role="math"><math><mn>1</mn></math></span>, <span aria-label="trzydzieści dziewięć" role="math"><math><mn>39</mn></math></span>
Na wykresie przedstawiono podział pracowników –osobowej firmy w zależności od wysokości pensji, jaką otrzymują.

- lat
- lat
- lat
- lat
W pięciu pojemnikach znajduje się średnio po cukru. Połącz w pary zdania z liczbami odpowiadającymi średniej arytmetycznej ilości cukru w pojemnikach.
<span aria-label="sto pięćdziesiąt pięć g" role="math"><math><mn>155</mn><mtext>g</mtext></math></span>, <span aria-label="sto pięćdziesiąt trzy g" role="math"><math><mn>153</mn><mtext>g</mtext></math></span>, <span aria-label="sto dziewięćdziesiąt g" role="math"><math><mn>190</mn><mtext>g</mtext></math></span>, <span aria-label="sto sześćdziesiąt dwa g" role="math"><math><mn>162</mn><mtext>g</mtext></math></span>, <span aria-label="sto pięćdziesiąt g" role="math"><math><mn>150</mn><mtext>g</mtext></math></span>
| Do trzech pojemników dosypano po cukru. | |
| Do dwóch pojemników dosypano po , a z jednego odsypano cukru. | |
| Do zestawu dołączono jeszcze jeden pojemnik, w którym jest cukru. | |
| Do każdego pojemnika dosypano po cukru. | |
| Z jednego pojemnika przesypano do pozostałych cukru. |