Symetria względem punktu
W tym materiale poznasz definicje symetrii środkowej oraz figur symetrycznych względem punktu. Dowiesz się, w jaki sposób rozpoznać i narysować takie figury. Rozwiążesz zadania dotyczące tych zagadnień.
Zapoznaj się z filmem i rozwiąż poniższe zadanie.
Film dostępny pod adresem /preview/resource/Rc4e28KPagQ5a
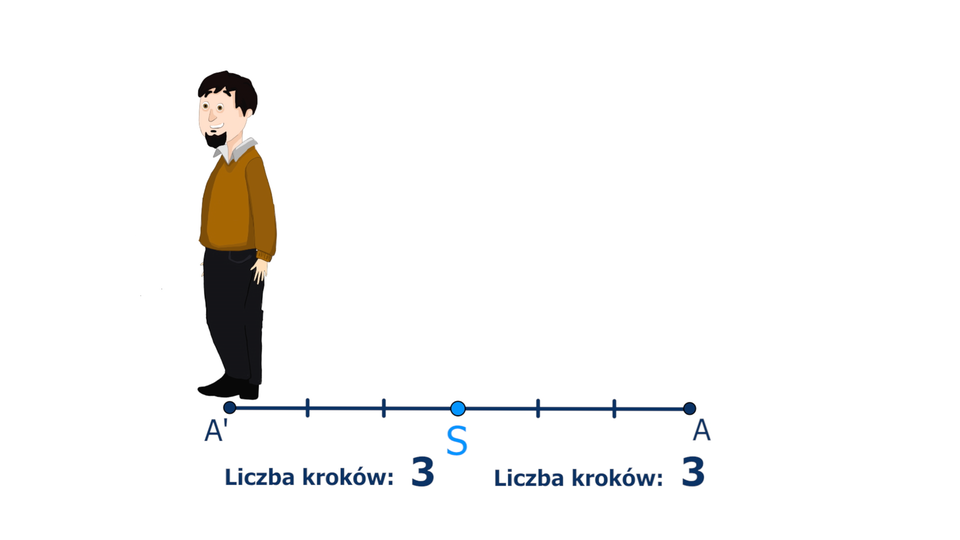
Animacja pokazuje, w jaki sposób powstaje punkt symetryczny do danego punktu względem innego punktu.
- Punkt leży na półprostej .
- Punkt leży na półprostej .
- Punkt jest środkiem odcinka .
- Długość odcinka jest równa długości odcinka .
- Punkt jest środkiem odcinka .
Punkt jest symetryczny do punktu względem punktu ( jest obrazem punktu w symetrii względem punktu ) jeżeli
leży na prostej po przeciwnej stronie punktu niż punkt ,
jego odległość od punktu jest równa odległości punktu od punktu .
Symetrię względem punktu nazywamy symetrią środkową.
Punkt jest środkiem odcinka .
Obrazem punktu w symetrii względem tego punktu jest punkt .
Jeżeli punkt jest obrazem punktu w symetrii względem punktu , to punkt jest obrazem punktu w tej samej symetrii.
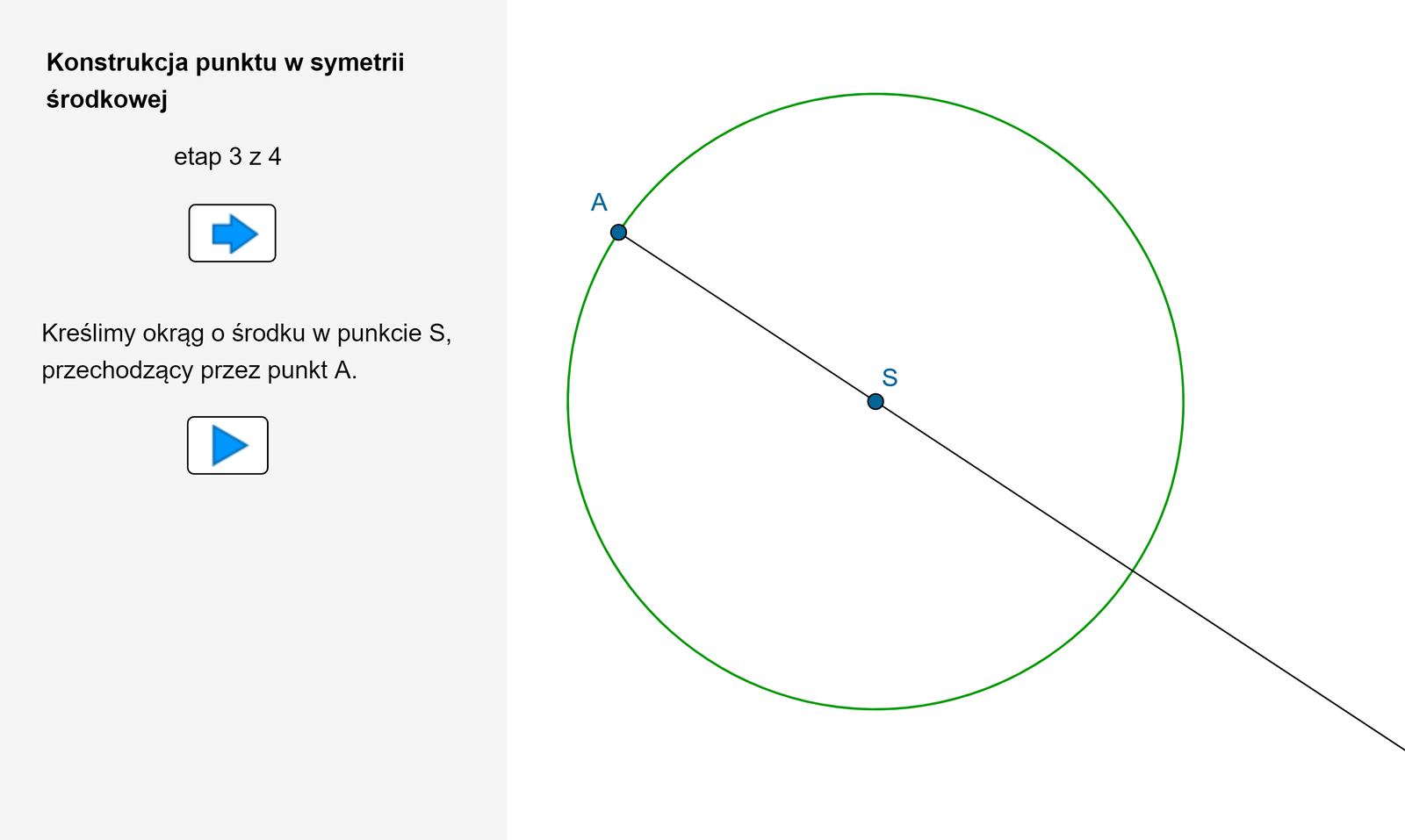
Zapoznaj się z poniższym apletem opisującym konstrukcję punktu w symetrii środkowej.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PPKpKYBux
Zauważmy, że aby skonstruuować punkt w symetrii środkowej, zamiast okręgu wystarczy narysować łuk. Wówczas konstrukcja przyjmie postać jak na poniższej animacji.

Film dostępny pod adresem /preview/resource/R1JP0G8v45NG7
Animacja pokazuje, w jaki sposób narysować punkt symetryczny do danego punktu względem innego punktu.
Opis konstrukcji:
Kreślimy półprostą .
Wykreślamy łuk o środku w punkcie i promieniu .
Punkt przecięcia tego łuku z półprostą oznaczamy . Jest on poszukiwanym obrazem punktu w symetrii środkowej względem .
Figury symetryczne względem punktu

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PPKpKYBux
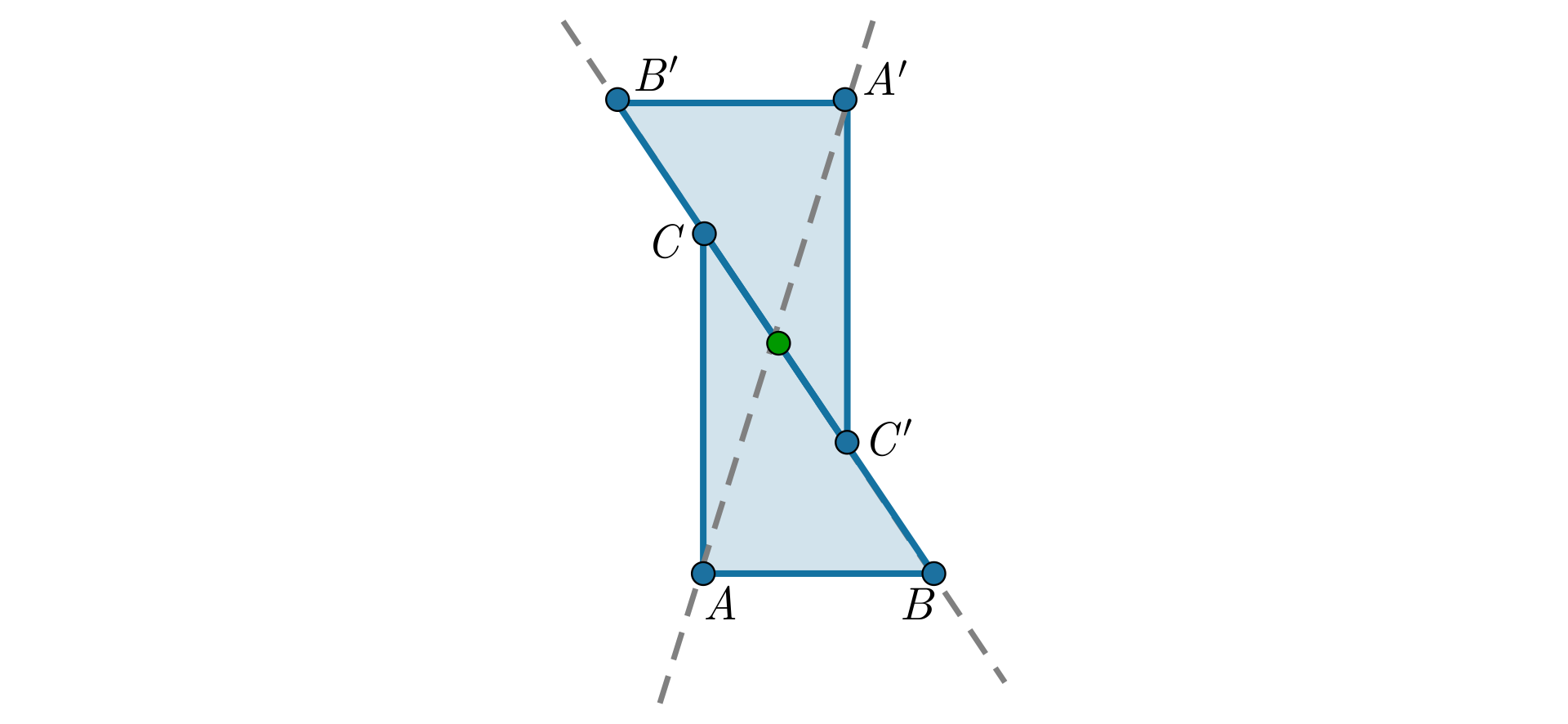
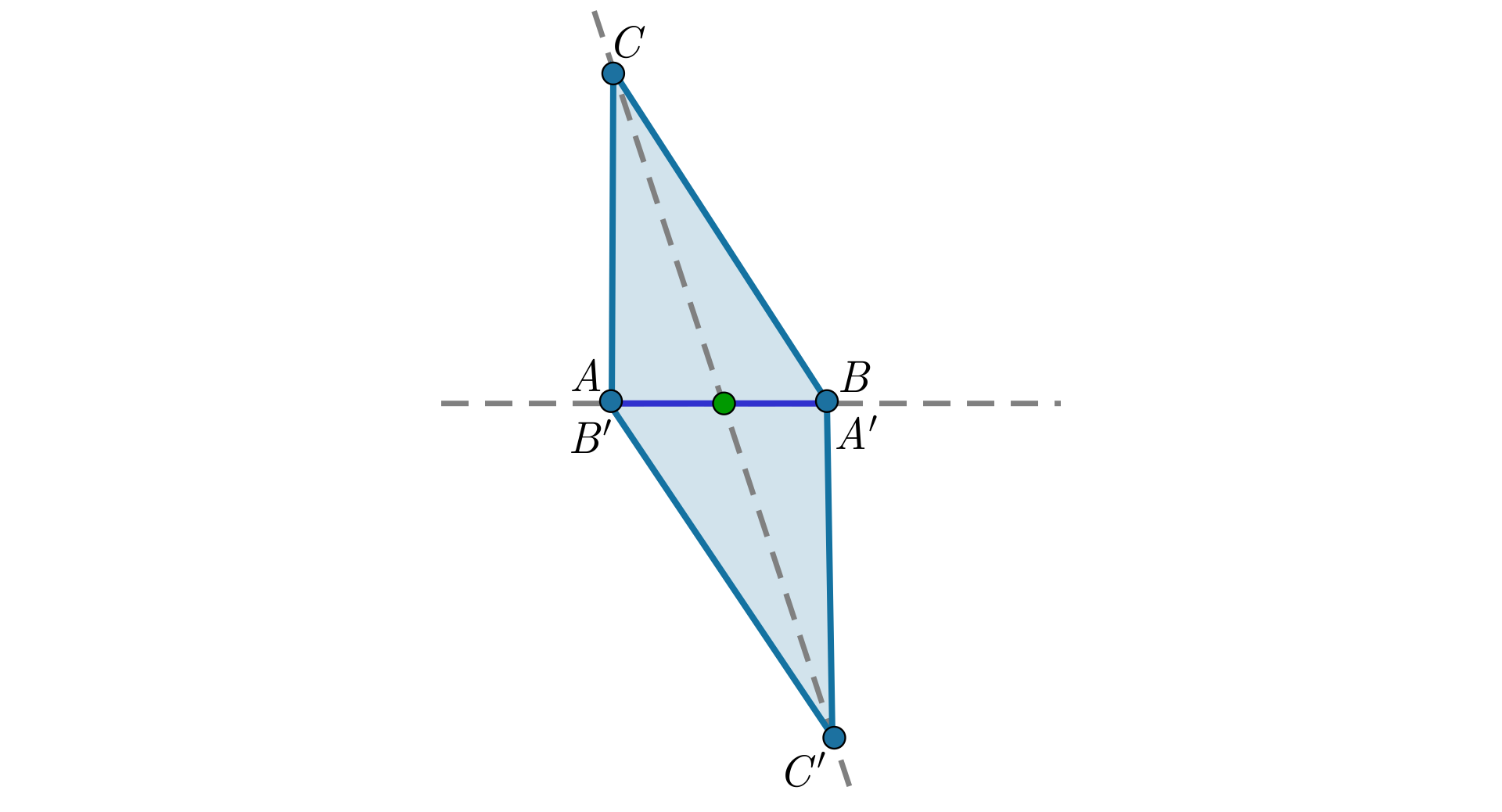
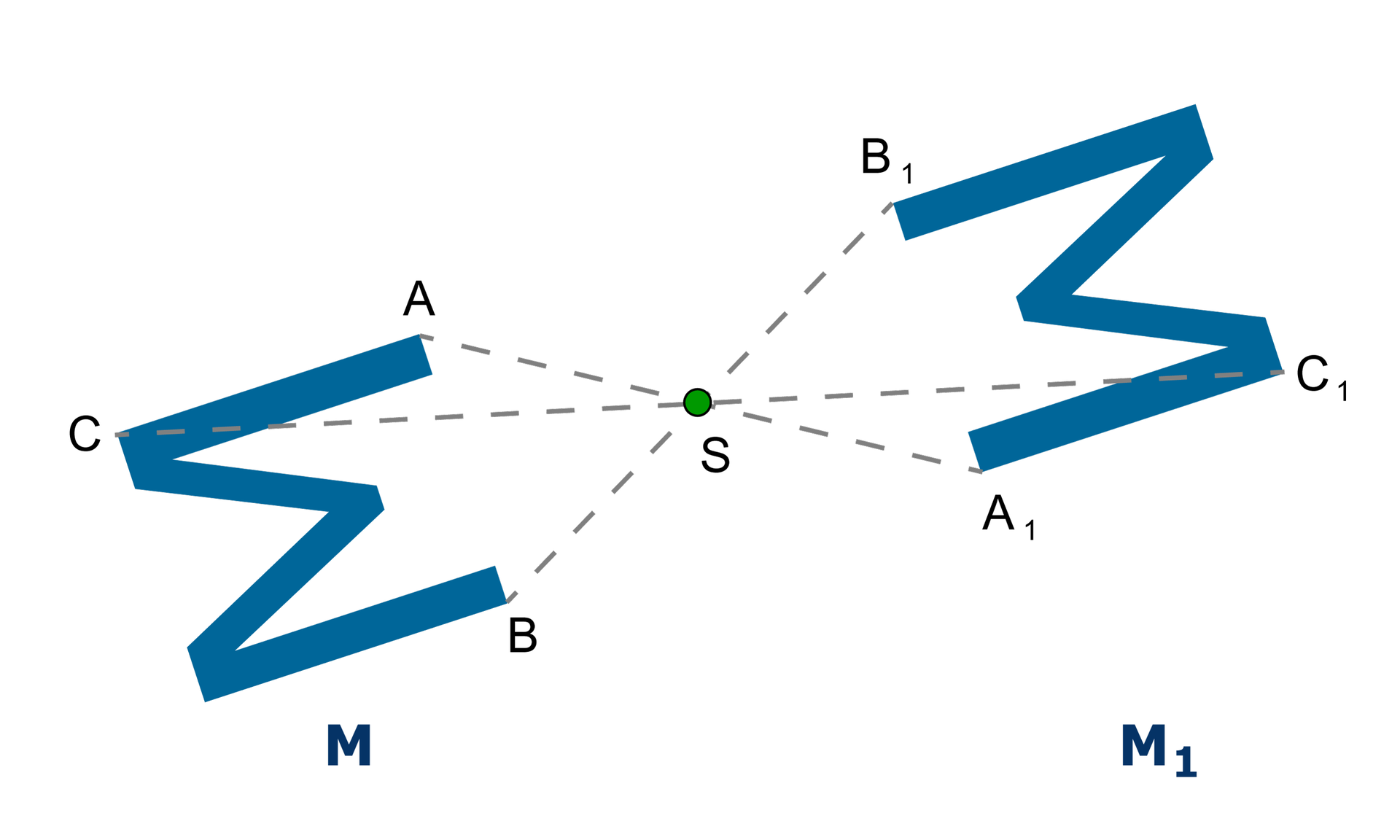
Figury i przedstawione na rysunku są symetryczne względem punktu . Oznacza to, że każdy punkt figury jest obrazem odpowiedniego punktu należącego do figury w symetrii względem punktu .
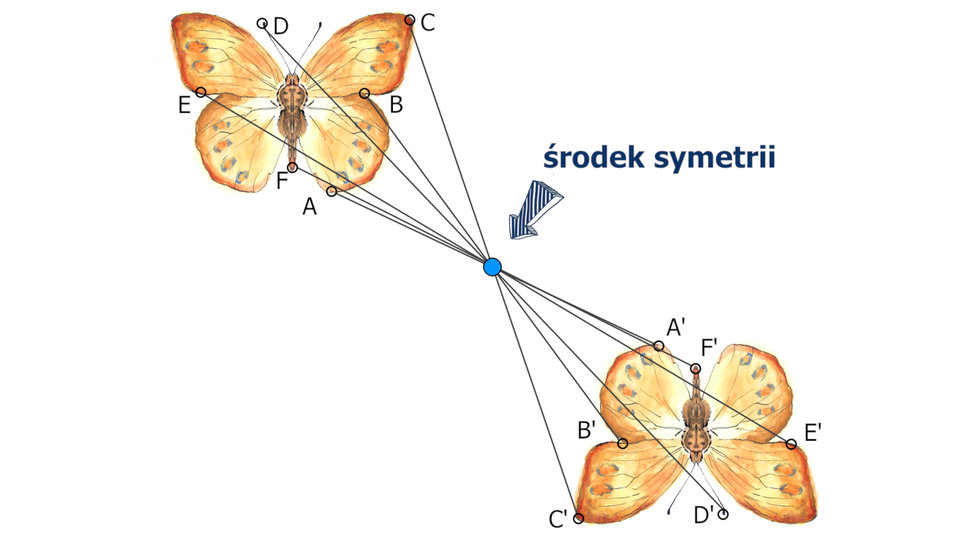
Film dostępny pod adresem /preview/resource/RHSXArxyeFrfm
Animacja przedstawia w jaki sposób uzyskujemy obraz figury w symetrii środkowej.
W symetrii środkowej obrazem:
odcinka jest odcinek tej samej długości,
koła jest koło o tym samym promieniu,
wielokąta jest wielokąt o tym samym kształcie, obwodzie i polu.
Jeżeli jest obrazem figury w symetrii względem punktu , to figura jest obrazem figury w tej samej symetrii.
Przykłady figur symetrycznych względem punktu
Oto przykłady figur środkowosymetrycznych.

Część figury składającej się z ośmiu łuków przekształcono w symetrii względem punktu .
Dokończ to przekształcenie, przemieszczając odpowiednie łuki.
Łuki można przemieszczać, zaczepiając kursor za punkty wyróżnione czerwonym kolorem.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PPKpKYBux
Zastanów się i odpowiedz na poniższe pytania.
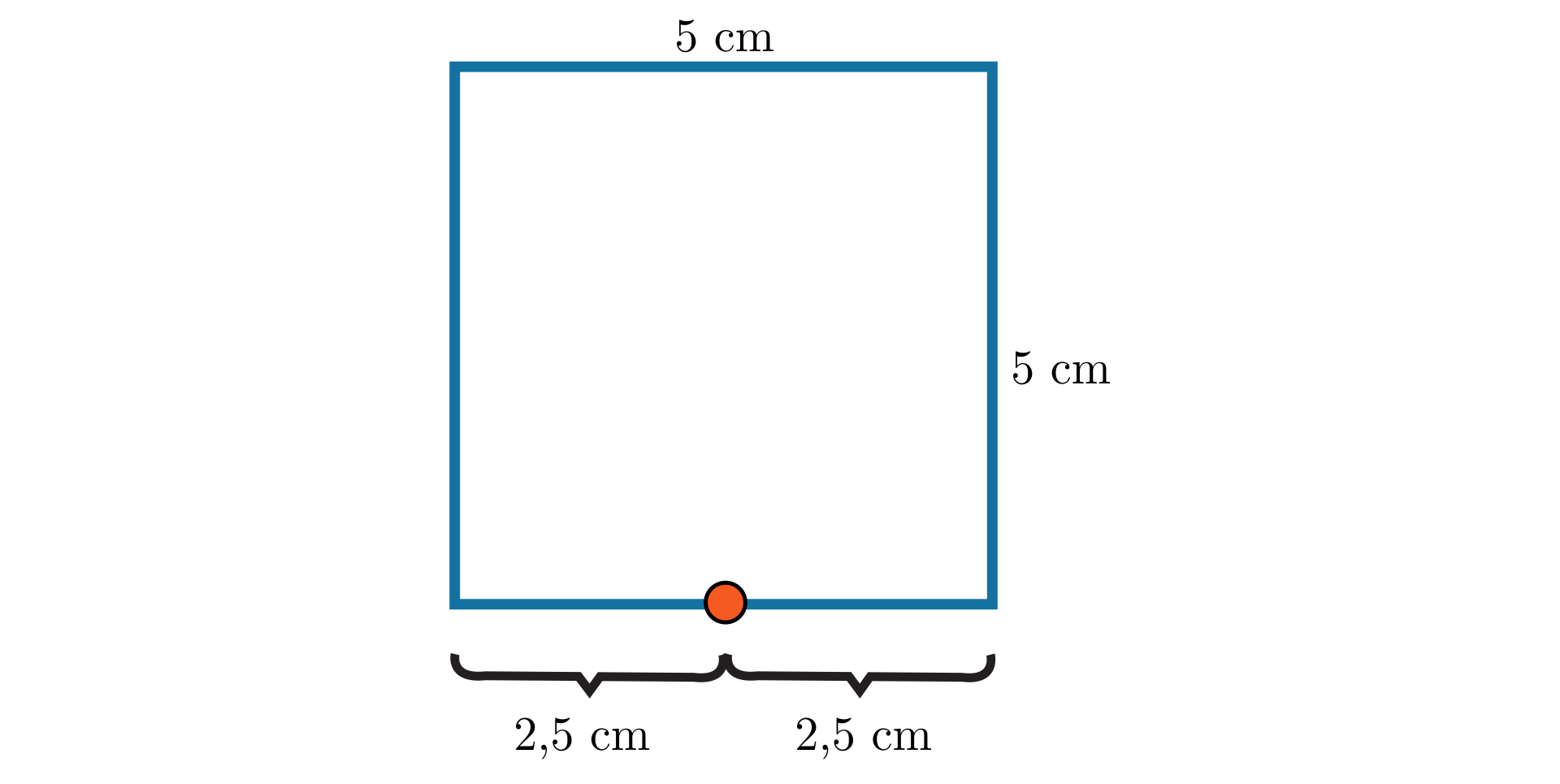
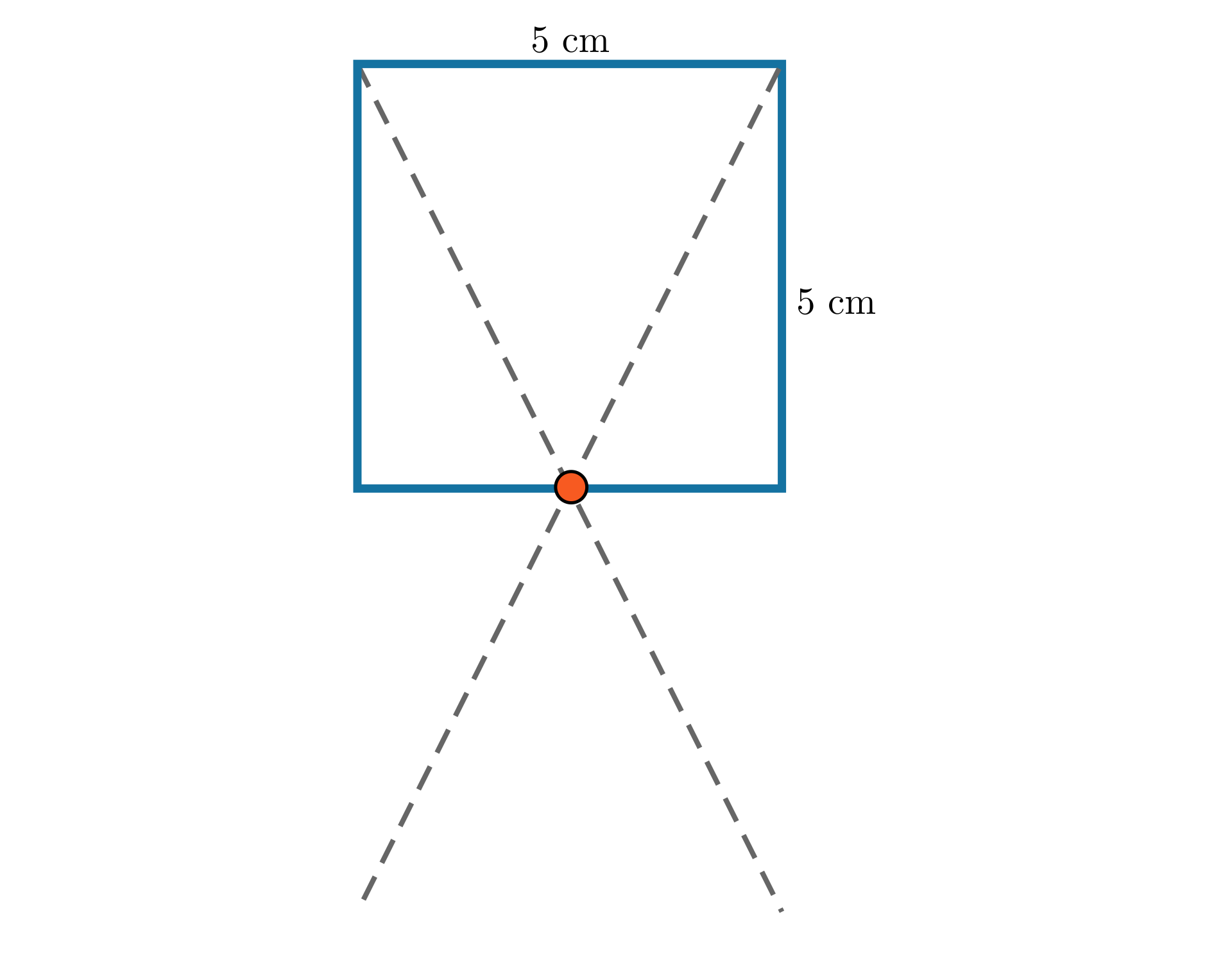
Zaznacz zdania prawdziwe. Możliwe odpowiedzi: 1. Obiekt symetryczny względem punktu to okrąg o promieniu 2 centymetry., 2. Obiekt symetryczny względem punktu to okrąg o promieniu 5 centymetrów., 3. Obiekt symetryczny względem punktu jest oddalony o 5 centymetrów od punktu., 4. Obiekt symetryczny względem punktu jest oddalony o 2 centymetry od punktu., 5. Środek okręgu wyjściowego jest oddalony o 2 centymetry od punktu., 6. Środek okręgu wyjściowego jest oddalony o 7 centymetrów od punktu., 7. Środki obu figur oddalone są od punktu o 7 centymetrów., 8. Odległość między środkami wynosi 10 centymetrów.
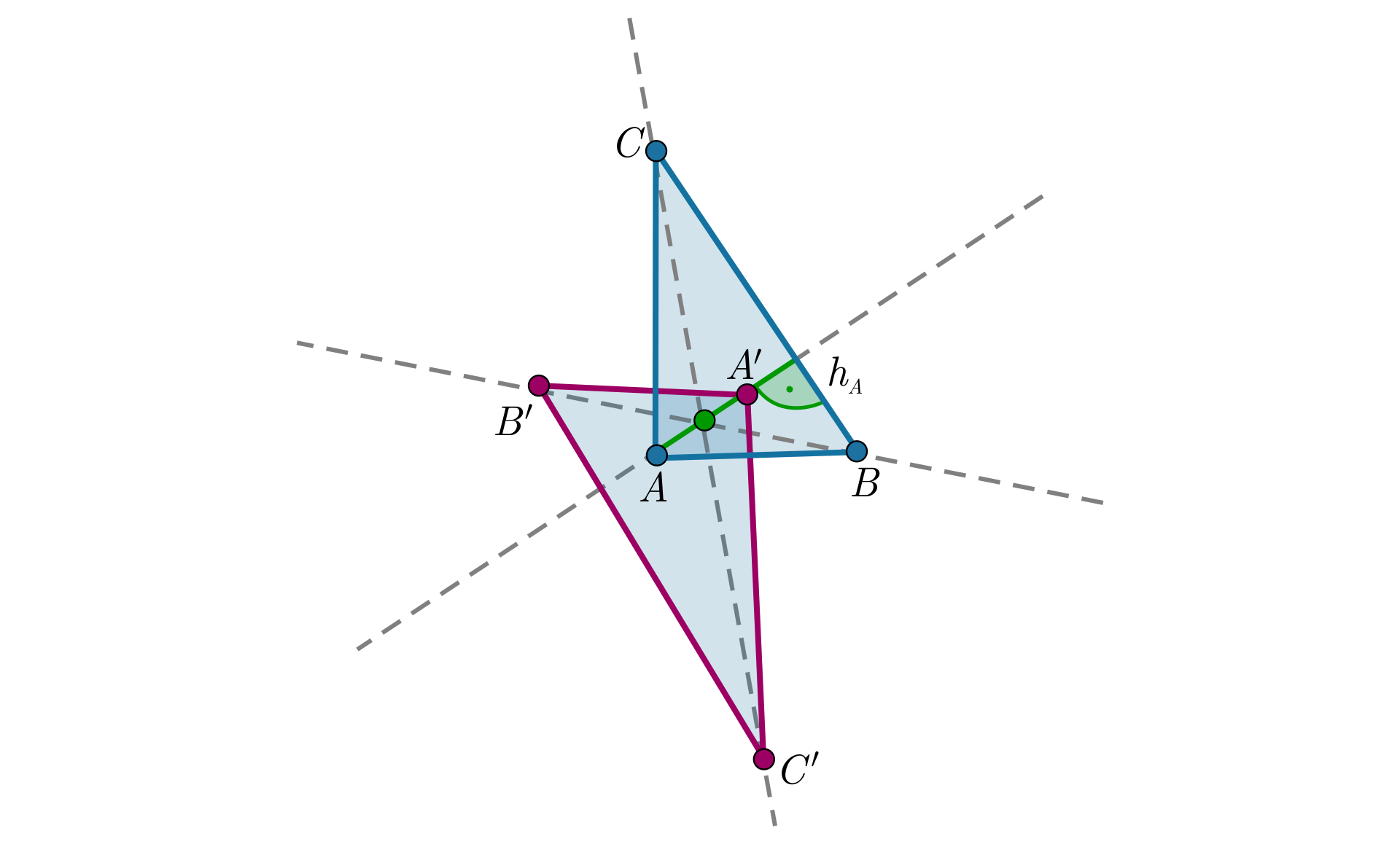
Narysuj dowolny trójkąt . Znajdź obraz tego trójkąta w symetrii względem punktu:
będącego jednym z jego wierzchołków,
leżącego wewnątrz trójkąta,
leżącego na zewnątrz trójkąta,
leżącego na jednym z boków trójkąta,
leżącego na jednej z wysokości trójkąta.
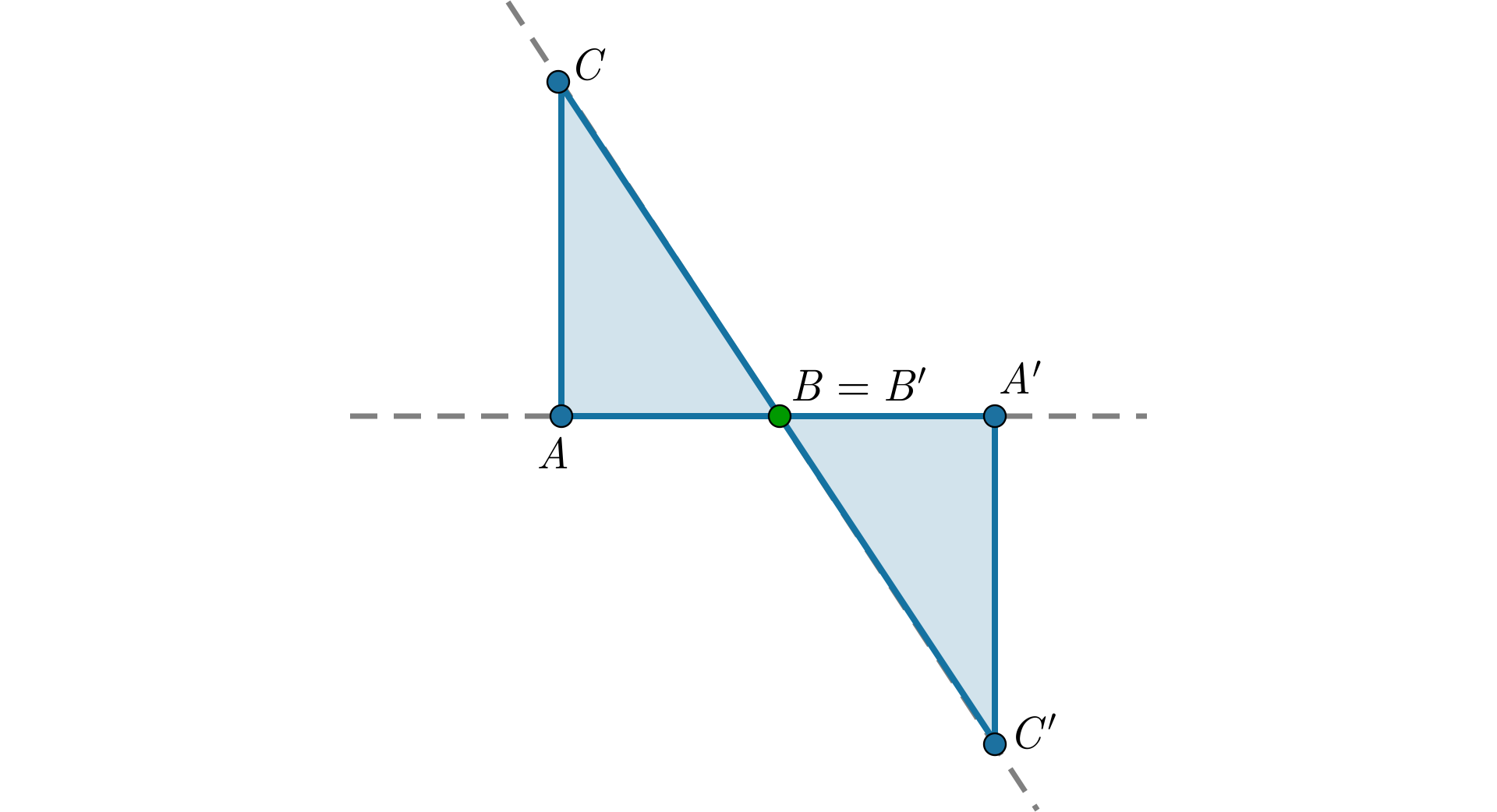
Jak będzie się przedstawiał obraz trójkąta w symetrii względem punktu:
będącego jednym z jego wierzchołków,
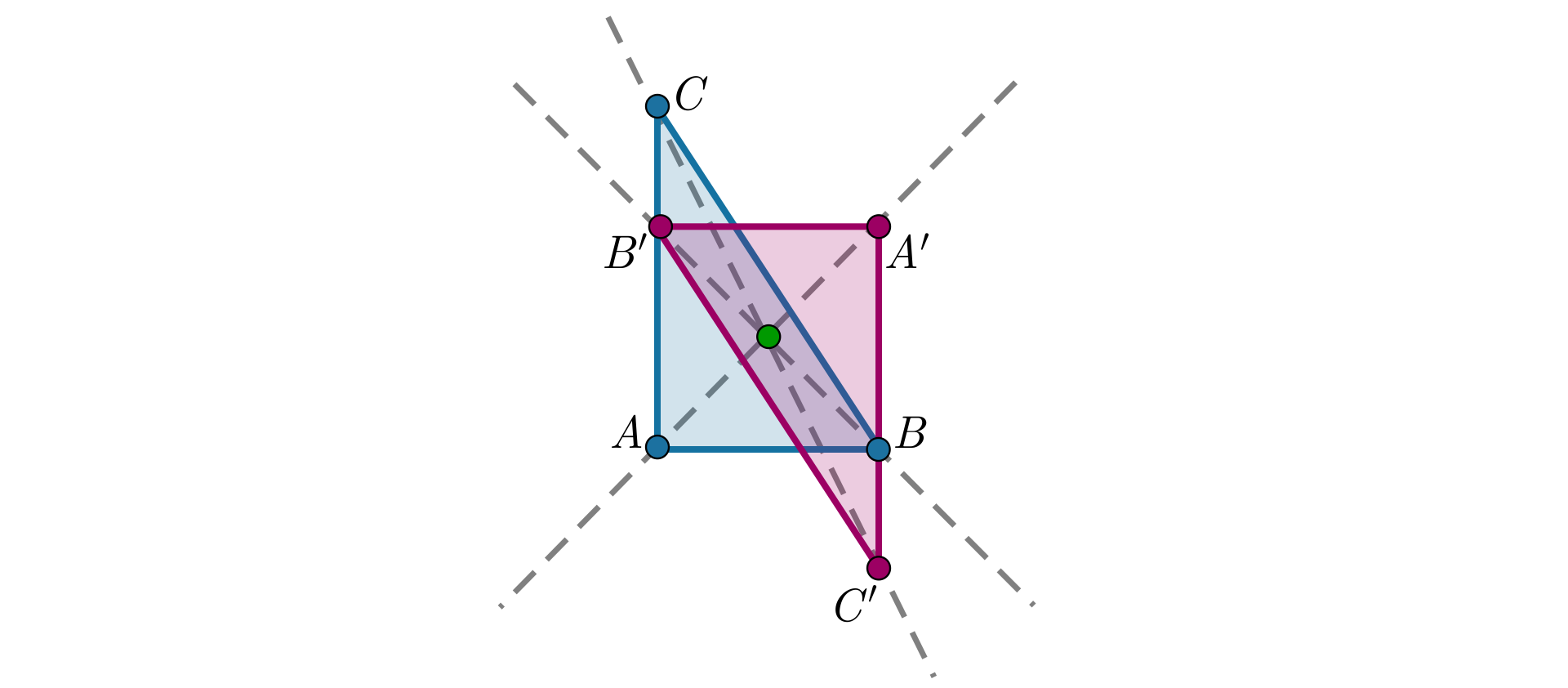
leżącego wewnątrz trójkąta,
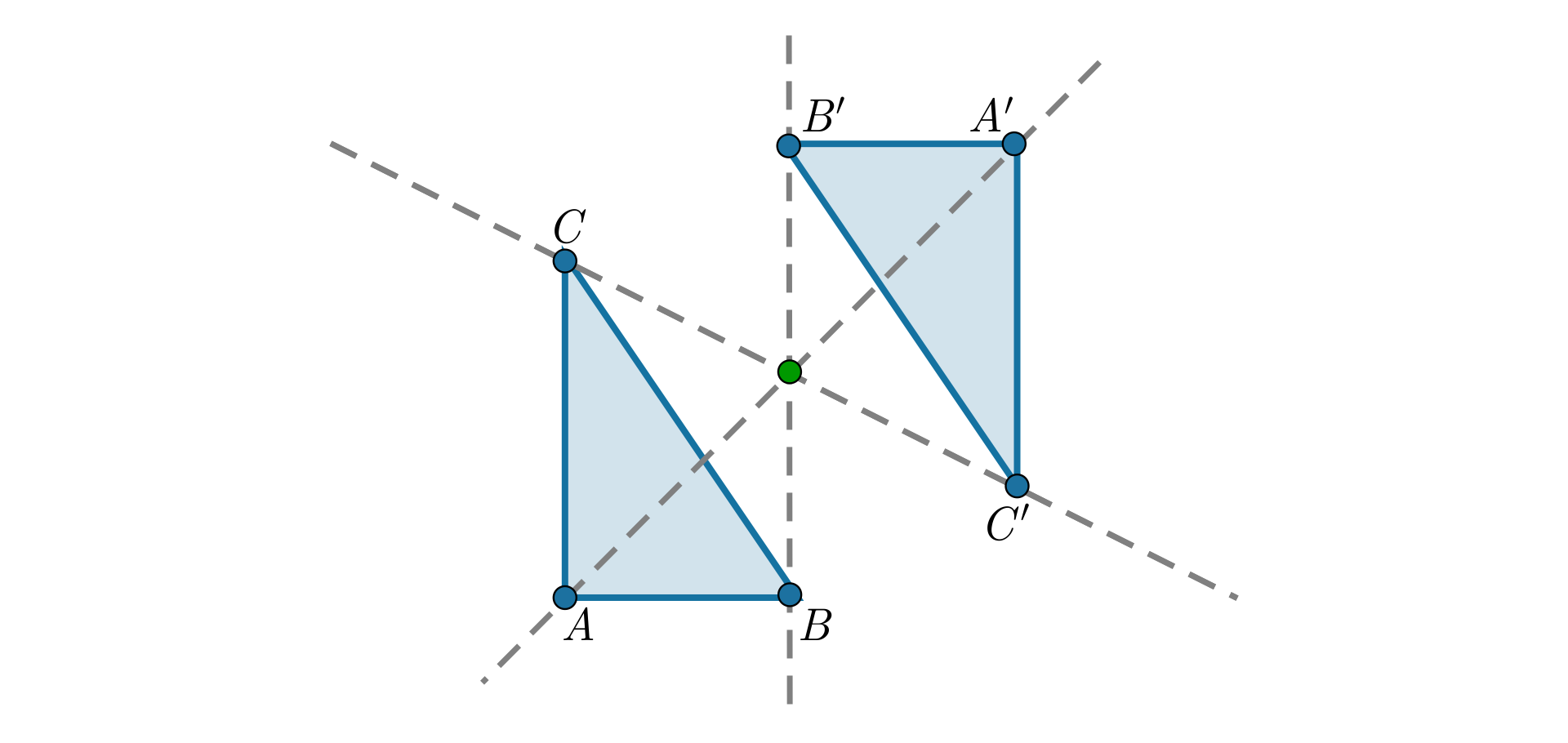
leżącego na zewnątrz trójkąta,
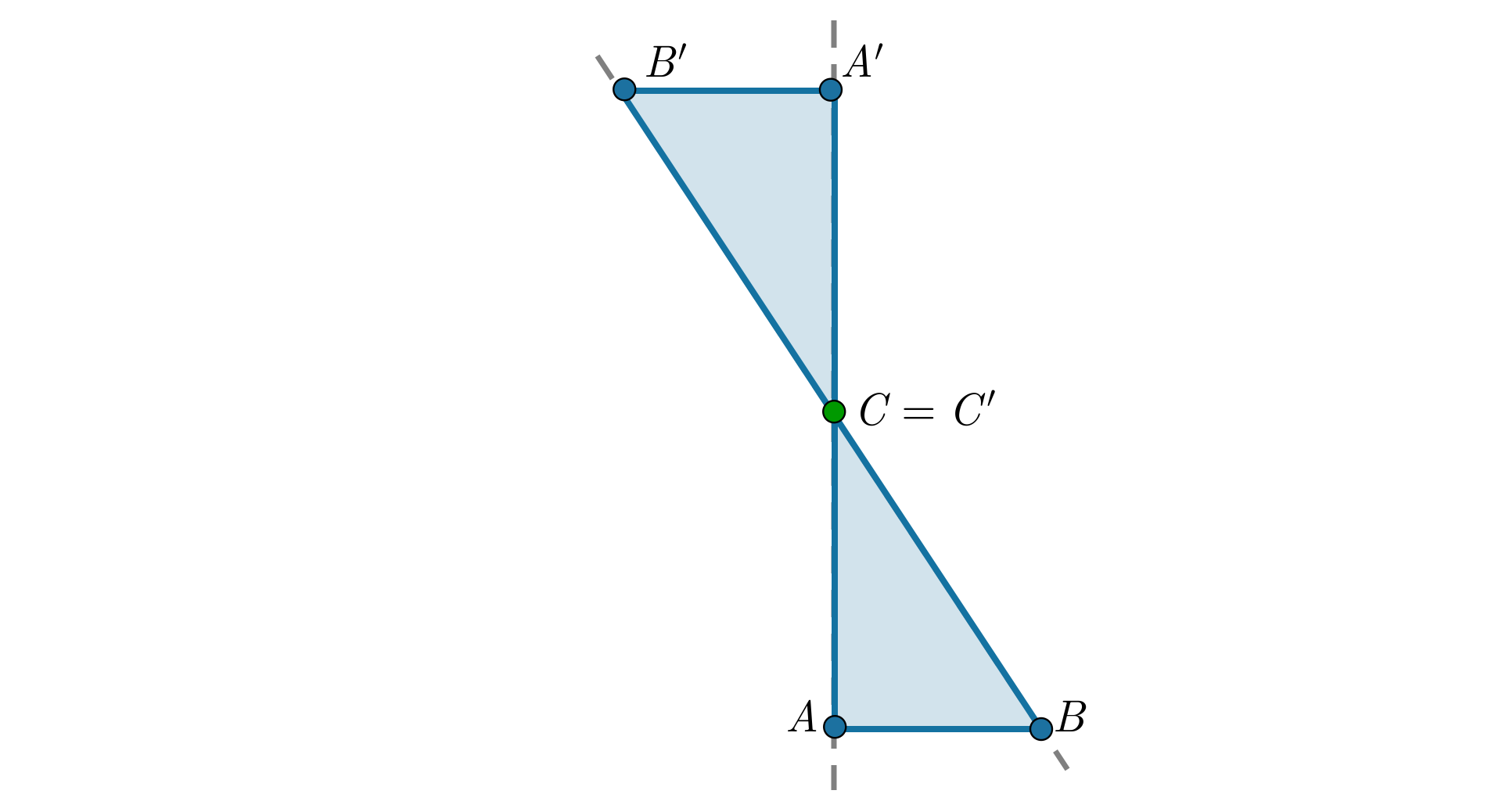
leżącego na jednym z boków trójkąta,
leżącego na jednej z wysokości trójkąta.
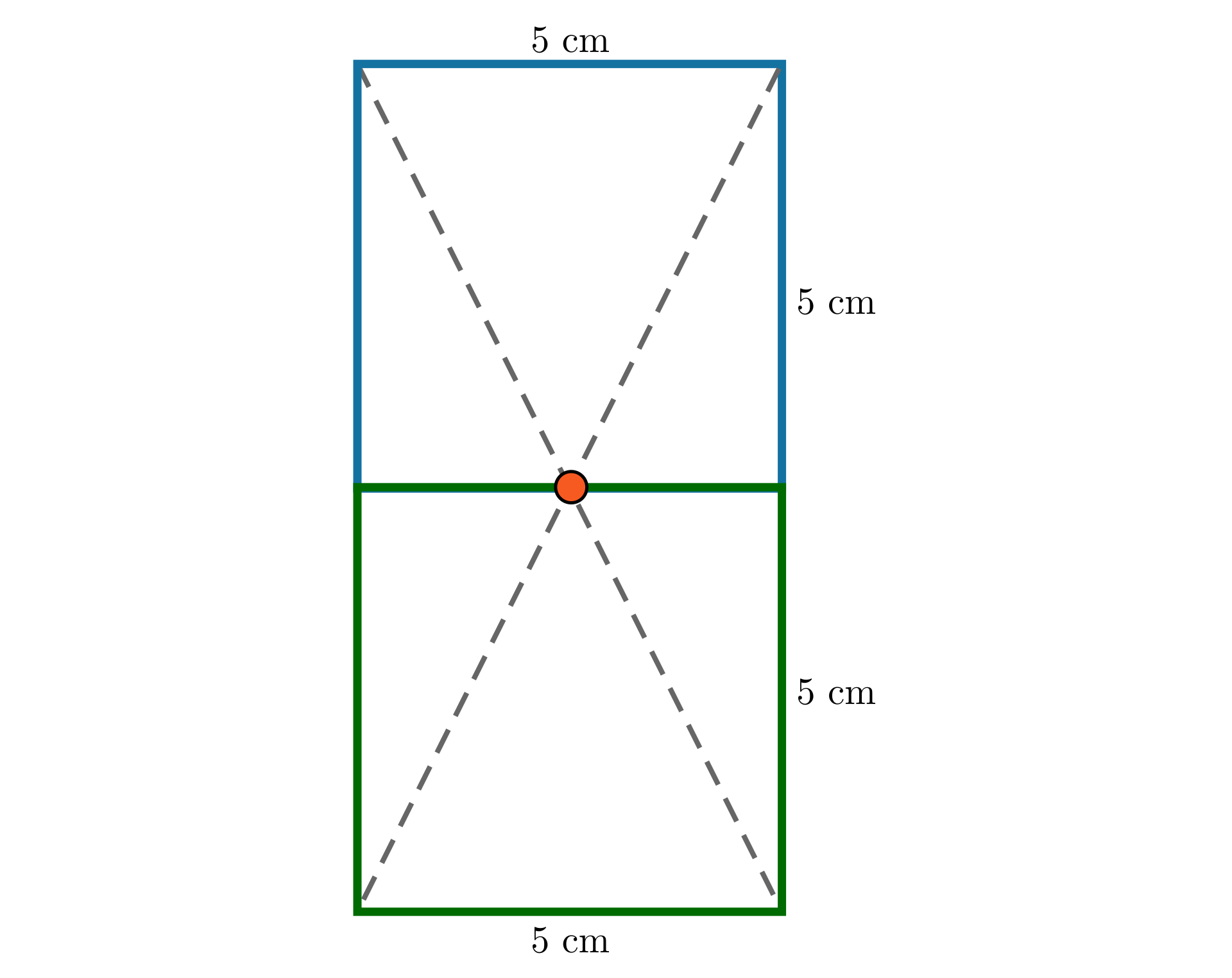
Uzupełnij zdanie, przeciągając w luki odpowiednie liczby i słowa lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Jest to 1. , 2. kwadrat, 3. , 4. prostokąt, 5. o polu 1. , 2. kwadrat, 3. , 4. prostokąt, 5. .
Uzupełnij zdania, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Długość odcinka wynosi 1. , 2. , 3. , 4. , 5. , 6. .
Obwód figury wynosi 1. , 2. , 3. , 4. , 5. , 6. .
Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. Pole wielokąta wynosi ., 2. Pole wielokąta wynosi ., 3. Pole wielokąta wynosi ., 4. Pole wielokąta wynosi .
Który z punktów jest symetryczny do punktu względem punktu ?

- punkt
- punkt
- punkt
- punkt
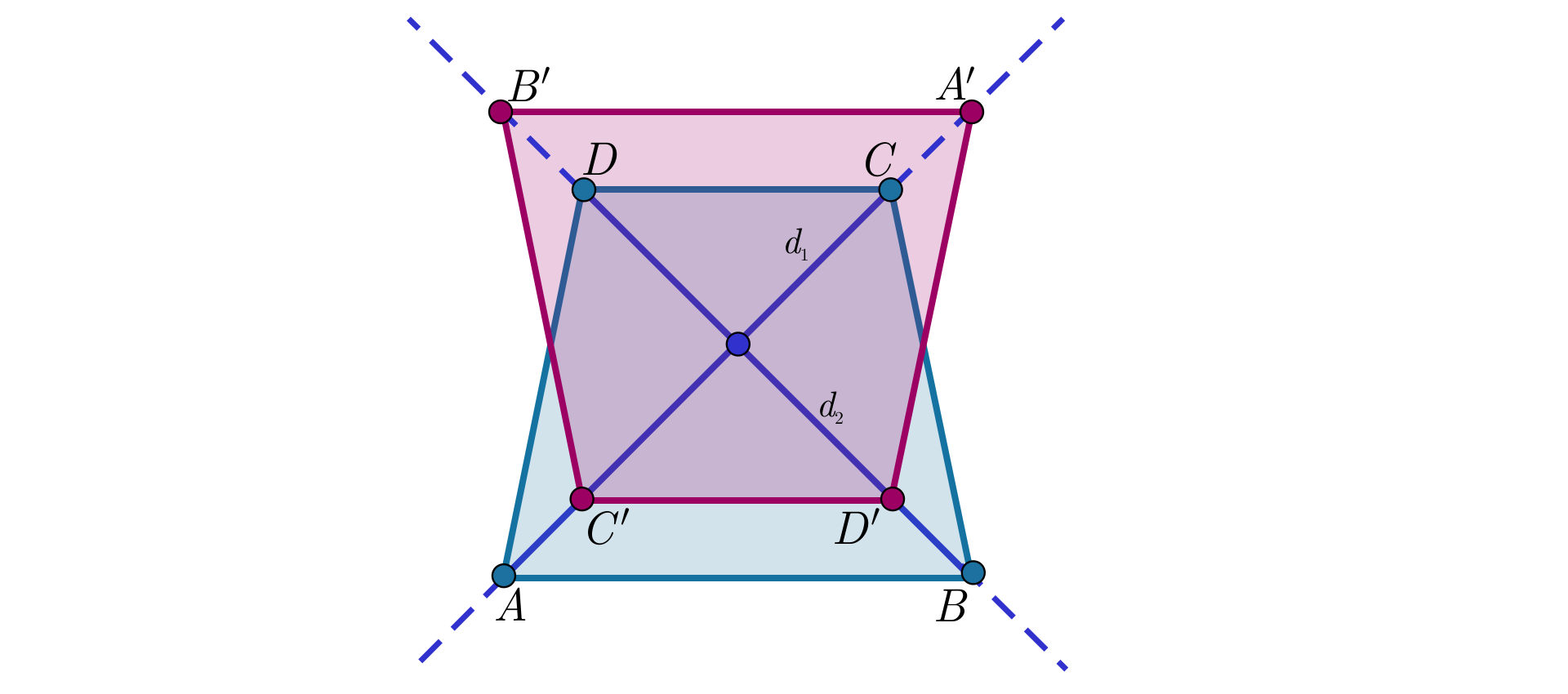
Narysuj dowolny trapez nie będący równoległobokiem. Znajdź obraz tego trapezu w symetrii względem punktu przecięcia jego przekątnych.
Jak będzie przedstawiał się dowolny trapez nie będący równoległobokiem, który odbijemy w symetrii względem punktu przecięcia jego przekątnych? Opisz własnymi słowami.
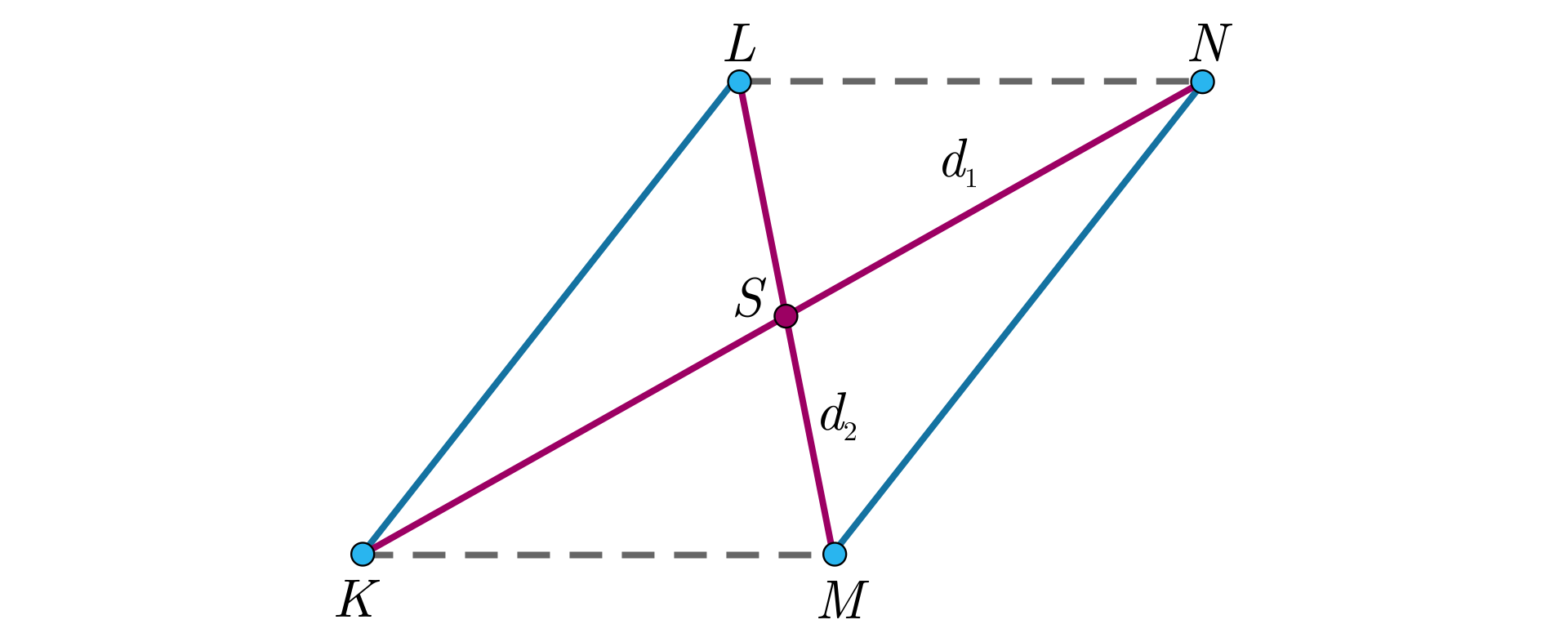
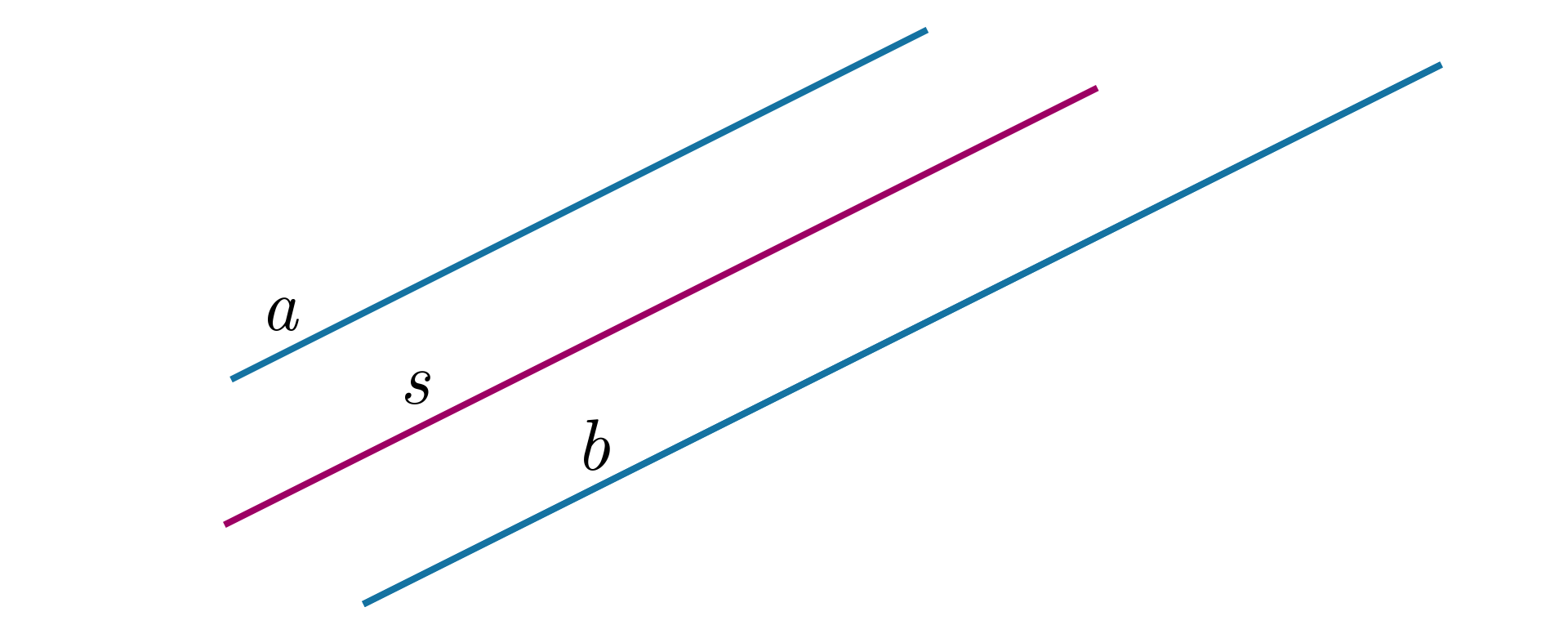
Narysuj dwa równoległe i równe odcinki i . Znajdź punkt , względem którego odcinek jest symetryczny do odcinka .
Mamy dwa równoległe odcinki o takiej samej długości i . Znajdź punkt , względem którego odcinek jest symetryczny do odcinka . Jak wyznaczyć punkt ? Opisz własnymi słowami.
Narysuj dwie proste równoległe i . Znajdź punkt , względem którego prosta będzie symetryczna do prostej . Czy istnieje tylko jeden taki punkt?
Mamy dwie proste równoległe i . Znajdź punkt , względem którego prosta będzie symetryczna do prostej . Czy istnieje tylko jeden taki punkt? Opisz tę konstrukcję własnymi słowami.