The exponential function and its properties. Transforming plots of the exponential function
Funkcja wykładnicza i jej własności. Przekształcanie wykresu funkcji wykładniczej
Learning objectives
You will learn to identify properties of the exponential function and to draw plots of functions , , , based on the plot of the function .
Learning effect
You identify properties of the exponential function and draw plots of functions , , , based on the plot of the function .
Prepare information divided in the following way:
The exponential functions – general formula, plot.
Properties of the exponential function.
Transformations of the plot of the function.
Check if information you prepared is the same as the following one.
1. The exponential functions – general formula, plot
The general formula of the exponential function: , where , a is a set positive number, different than 1.
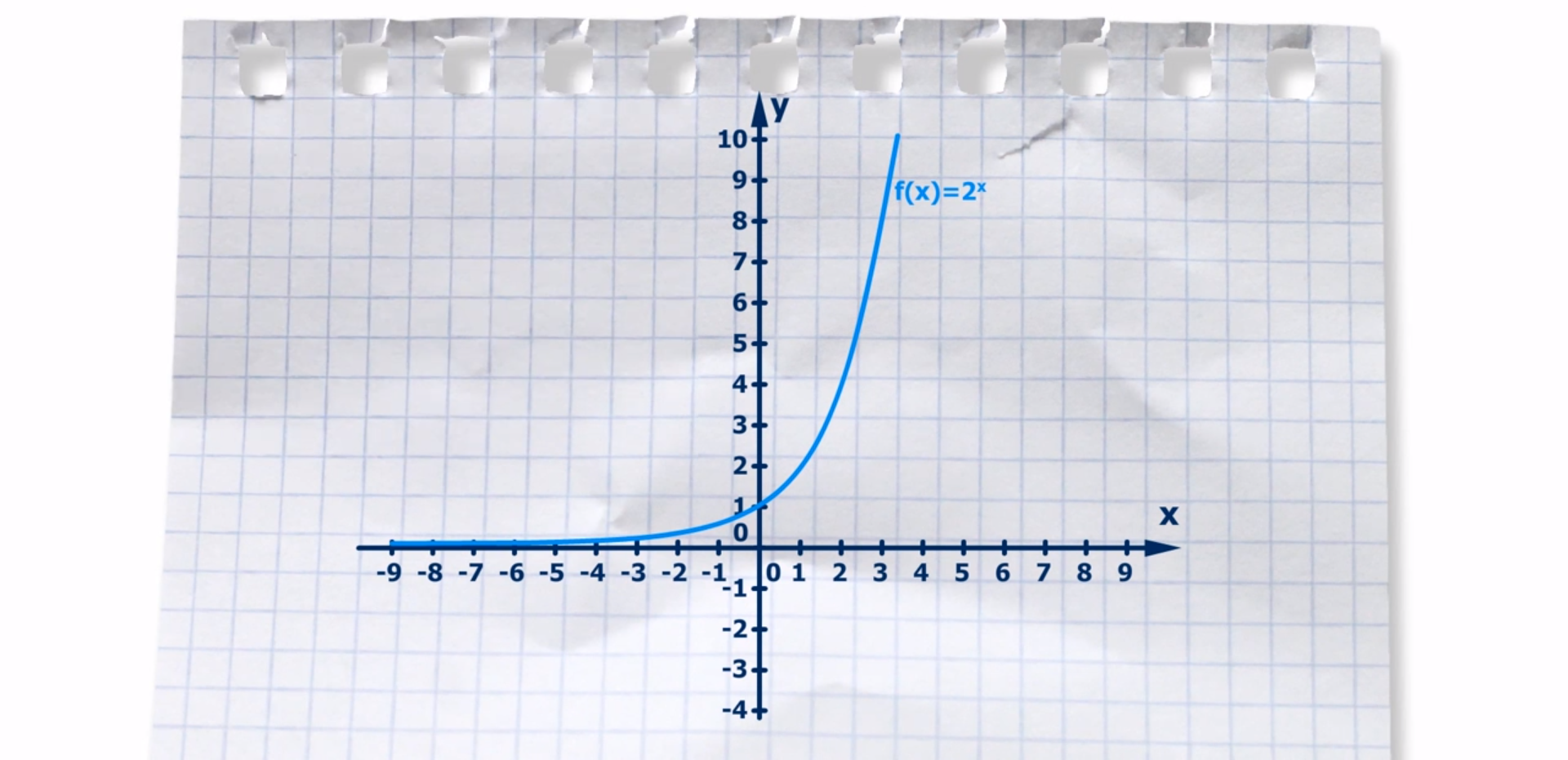
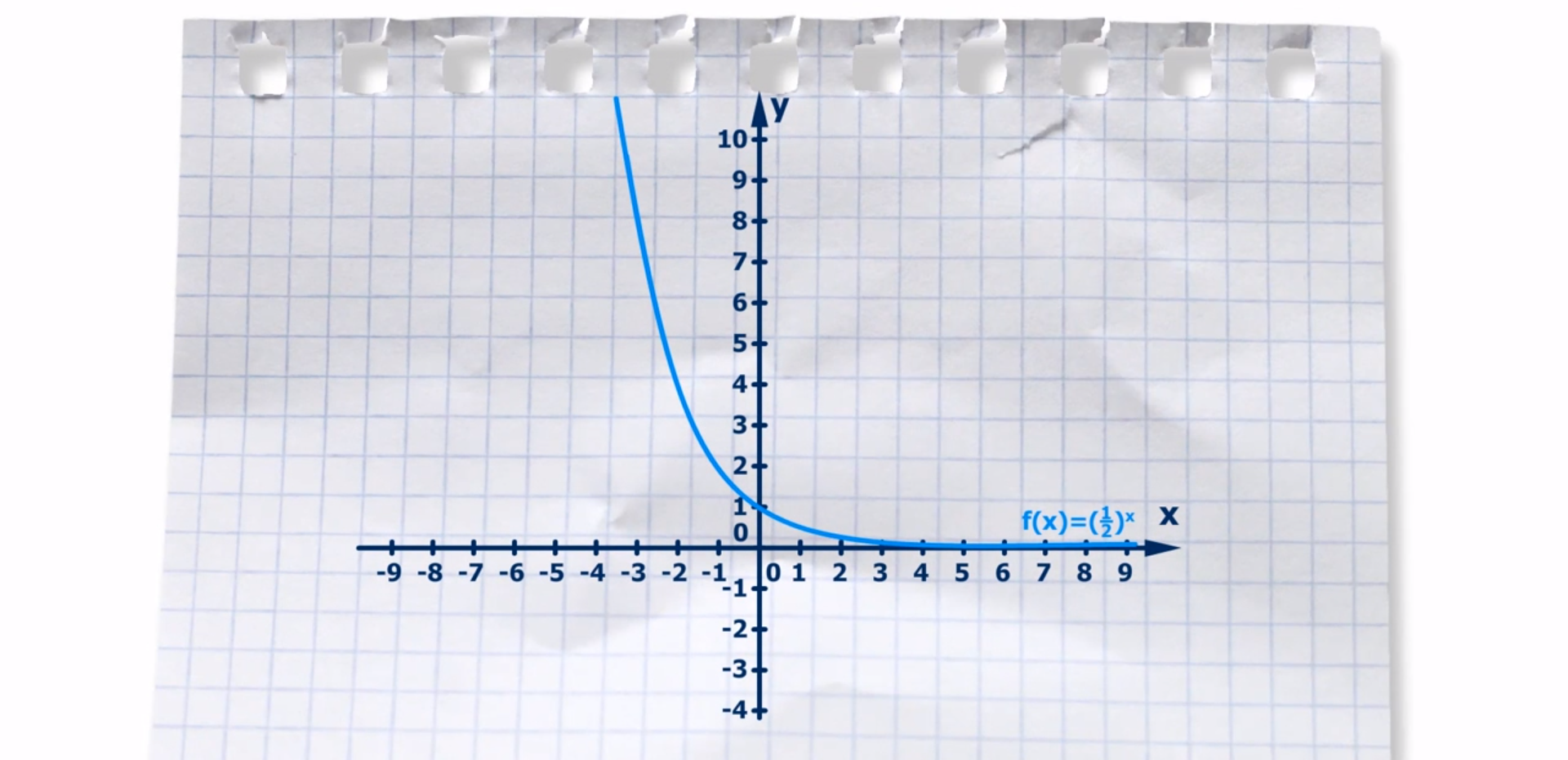
2. Properties of the exponential function:
the domain of the function is the set of all real numbers,
the range of the function is the interval (0,+∞),
the asymptote of the function is the line y=0
there are no roots,
it is monotonic and if a>1, then the function f is increasing and if 0<a<1, then the function is decreasing,
it is injective, so each value is taken by only one argument,
the plot of the function crosses the axis Y in the point (0,1).
3. Transformation of the plot of the function:
By transforming the plot of the function by units along the X axis in accordance with the direction of the axis, we obtain the plot of the function .
By transforming the plot of the function by units along the Y axis in accordance with the direction of the axis, we obtain the plot of the function .
By transforming the plot of the function in axial symmetry with respect to the X axis, we obtain the plot of the function .
By transforming the plot of the function in axial symmetry with respect to the Y axis, we obtain the plot of the function .
Open the applet and analyse how the plot of the exponential function changes in discusses transformations.
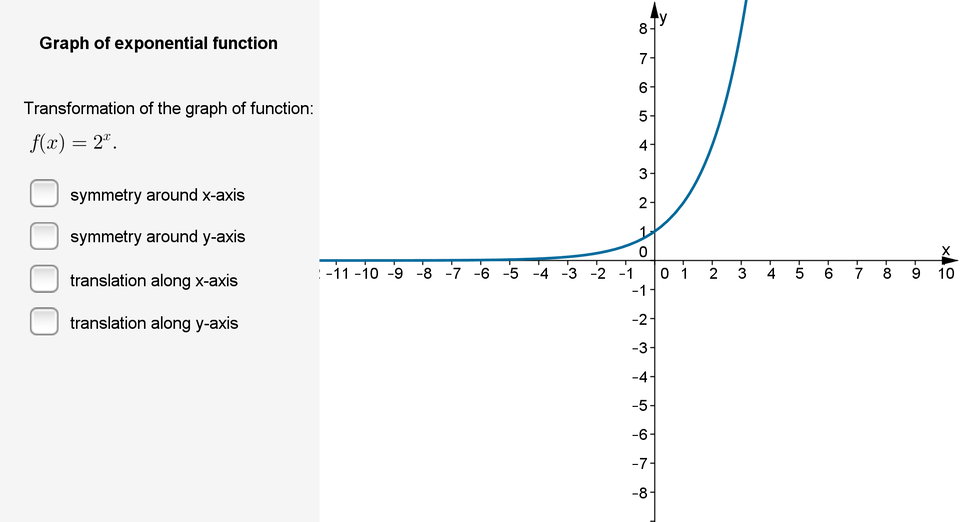
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D19ucpf8A
After having completed the exercise, write down formulas of functions obtain as a result of presented transformations.
By transforming the plot of the function by units along the X axis in accordance with the direction of the axis, we obtain the plot of the function .
By transforming the plot of the function by units along the Y axis in accordance with the direction of the axis, we obtain the plot of the function .
By transforming the plot of the function in axial symmetry with respect to the X axis, we obtain the plot of the function
.By transforming the plot of the function in axial symmetry with respect to the Y axis, we obtain the plot of the function .
Draw in one coordinate system plots of functions and . What can you say about the mutual position of plots of these functions?
Draw the plot of the function and identify its properties.
In the drawing there is the plot of the exponential function. On separate pieces of paper, draw plots of functions after given transformations. Write formulas of obtained functions.
Transformations:
a. translation by 3 units to the right along the X axis,
b. translation by 2 units up along the Y axis,
c. symmetry with respect to the X axis,
d. symmetry with respect to the Y axis.
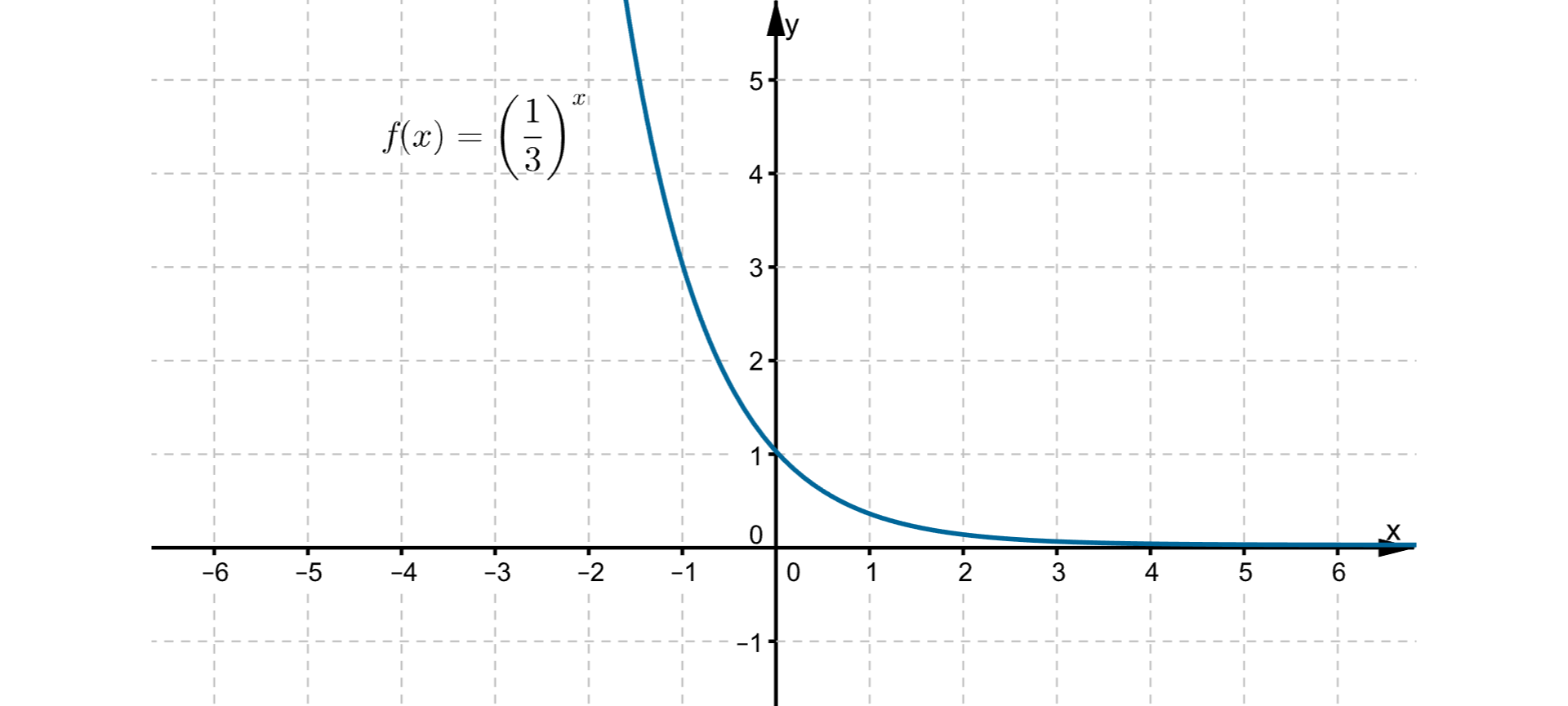
Draw the plot of the function .
Remember
The general formula of the exponential function: , where , a is a set positive number, different than 1.
Properties of the exponential function:
the domain of the function is the set of all real numbers,
the range of the function is the interval (0,+∞),
the asymptote of the function is the line y=0,
there are no roots,
it is monotonic and if a>1, then the function f is increasing and if 0<a<1, then the function is decreasing,
it is injective, so each value is taken by only one argument,
the plot of the function crosses the axis Y in the point (0,1).
By transforming the plot of the function by p units along the X axis in accordance with the direction of the axis, we obtain the plot of the function .
By transforming the plot of the function by q units along the Y axis in accordance with the direction of the axis, we obtain the plot of the function .
By transforming the plot of the function in axial symmetry with respect to the X axis, we obtain the plot of the function .
By transforming the plot of the function in axial symmetry with respect to the Y axis, we obtain the plot of the function .
Exercises
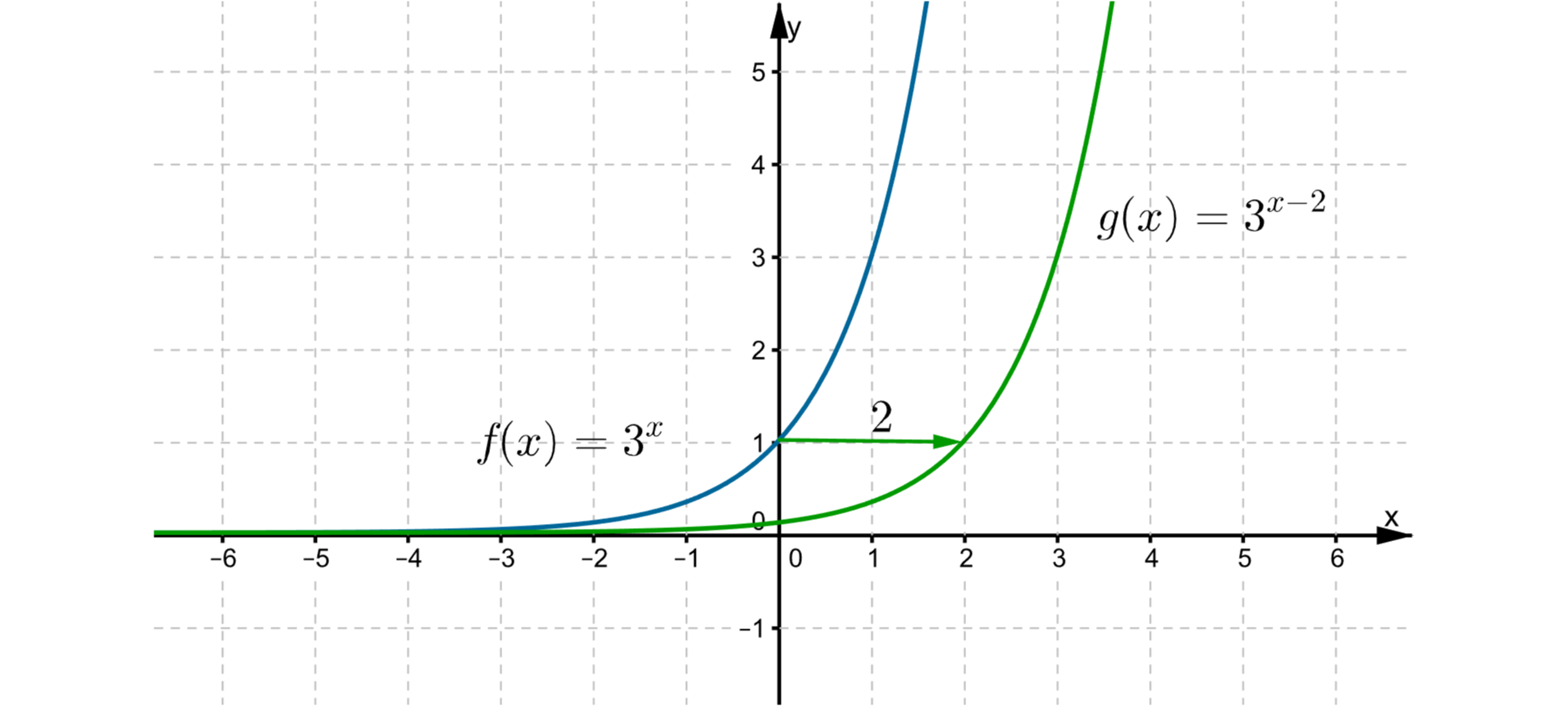
What transformation is presented in the graph?
- Symmetry with respect to the X axis.
- Translation along the X axis.
- Symmetry with respect to the Y axis.
- Translation along the Y axis.
Draw the plot of the function
.
Then draw plots of functions:
Draw the plot of the function . Identify properties of this function in English.
Indicate which pairs of expressions or words are translated correctly.
- funkcja wykładnicza - exponential function
- asymptota wykresu funkcji wykładniczej - asymptote of the plot of the exponential function
- monotoniczność - monotonicity
- różnowartościowość - injectiveness
- przesunięcie wykresu funkcji wzdłuż osi OX - the plot of the function y = - ax
- asymptota wykresu funkcji wykładniczej - exponential function
- monotonicity
- the asymptote of the plot of the exponential function
- injectiveness
- asymptota wykresu funkcji wykładniczej
- wykres funkcji
- różnowartościowość
- exponential function
- graph of the function
- monotoniczność
- funkcja wykładnicza
Glossary
asymptota wykresu funkcji wykładniczej - prosta o równaniu y = 0
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: asymptote of the plot of the exponential function
funkcja wykładnicza - funkcja określona wzorem , gdzie , a jest ustaloną liczbą dodatnią i różną od 1.
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: exponential function
funkcja
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: function
różnowartościowość
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: injectiveness
monotoniczność
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: monotonicity
symetria względem osi OX
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: symmetry along the X axis
symetria względem osi OY
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: symmetry along the Y axis
przesunięcie wykresu funkcji wzdłuż osi OX
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: translation of the plot along the X axis
przesunięcie wykresu funkcji
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: translation of the plot of the function
Keywords
asymptote of the plot of the exponential functionasymptote of the plot of the exponential function - the line y =
exponential functionexponential function – a function defined by the formula , where , a is a set positive number, different than 1
injectivenessinjectiveness
monotonicitymonotonicity




