Budowa walca

Przykład 1

W jakim kształcie są wieże na zdjęciach? Jakie bryły geometryczne przypominają?

R1PSEcIRIhTtV1

Zdjęcia trzech różnych budowli w kształcie okrągłej wieży. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przykład 2

Zmieniaj wymiary obracającego się prostokąta. Jaka jest zależność między wysokością otrzymywanego walca a jego tworzącą? Jaka jest zależność między promieniem podstawy walca a długością boku prostokąta prostopadłego do osi obrotu?

R1Ef62TllcZa51

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DvaowsLHi

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY NC 3.0.

W wyniku obrotu prostokąta wokół prostej przechodzącej przez jeden z boków otrzymujemy bryłę, zwaną walcem.
Walec ma dwie równoległe podstawy w kształcie przystających kół. Odcinek łączący podstawy walca i prostopadły do tych podstaw to wysokość walca. Wysokość jest równa odległości podstaw walca.
Każdy odcinek zawarty w powierzchni bocznej walca o końcach należących do podstaw walca nazywamy tworzącą. Długość tworzącej walca jest równa jego wysokości.

Przykład 3

Określ dla każdego z walców jego wysokość, długość tworzącej, promień podstawy i średnicę podstawy.

R4wKiiebkYdmY1

Rysunki czterech walców. Pierwszy walec ma wysokość równą 31 cm i średnicę podstawy 6 cm. Drugi walec ma wysokość równą 19 mm i średnicę podstawy 7 mm. Trzeci walec ma wysokość równą 15 cm i średnicę podstawy 17 cm. Czwarty walec ma wysokość równą 2 dm i średnicę podstawy 0,5 dm. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przekroje walca

Przykład 4

RRxZPpCqBmsjI1

Przykład 5

R1a6j2O8Pmk6L1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przykład 6

R17RQtiriYrJ41

Rysunki walca z zaznaczonym przekrojem poprzecznym (w kształcie koła) i koła o takim samym promieniu r. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RP1d9lrLyaIhR1

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DvaowsLHi

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY NC 3.0.

Przykład 7

RKFyxSh44CVLp1

Rysunek walca o wysokości H z zaznaczonym przekrojem osiowym (w kształcie prostokąta) oraz prostokąta o bokach długości H i 2r. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przykład 8

Przekrój osiowy walca jest prostokątem o szerokości $9 cm$ . Pole tego przekroju jest równe $108 {cm}^{2}$ .
Określ wysokość i promień podstawy walca.
Obliczamy długość prostokąta, będącego przekrojem osiowym walca.

108 {cm}^{2} : 9 cm = 12 cm

Prostokąt, będący przekrojem osiowym walca, ma wymiary $9 cm$ na $12 cm$ .
Możliwe są dwa przypadki.

Rwv7uqEMx0IE51

Rysunki dwóch walców. Pierwszy o wysokości H =9 cm i średnicy podstawy d =12 cm. Drugi o wysokości H =12 cm i średnicy podstawy d =9 cm. Zaznaczone przekroje osiowe. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

$I$ przypadek
Wysokość walca jest równa $9 cm$ , a promień jego podstawy jest równy $12 cm : 2 = 6 cm$ .
$II$ przypadek
Wysokość walca jest równa $12 cm$ , a promień jego podstawy jest równy $9 cm : 2 = 4,5 cm$ .

Przykład 9

Przekrój osiowy walca jest prostokątem, którego przekątna długości $20 cm$ jest nachylona do dłuższego boku pod kątem $30 °$ . Wysokość walca jest równa długości tego prostokąta. Oblicz pole podstawy walca.

R3EiPqPnX0deE1

Rysunek walca z zaznaczonym przekrojem osiowym w kształcie prostokąta. Przekątna prostokąta ma długość 20 cm. Zaznaczony kąt, jaki tworzy przekątna prostokąta z jego bokiem wynosi 30 stopni. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przekątna dzieli prostokąt, będący przekrojem osiowym walca, na dwa przystające trójkąty prostokątne.
Przeciwprostokątna w tak otrzymanym trójkącie ma długość $20 cm$ , a jeden z kątów ostrych ma miarę $30 °$ . W takim trójkącie naprzeciw kąta o mierze $30 °$ leży przyprostokątna dwa razy krótsza od przeciwprostokątnej, czyli w tym przypadku o długości $20 cm : 2 = 10 cm$ . Druga z przyprostokątnych ma długość $10 \sqrt{3} cm$ .

RXRznmwwv52oT1

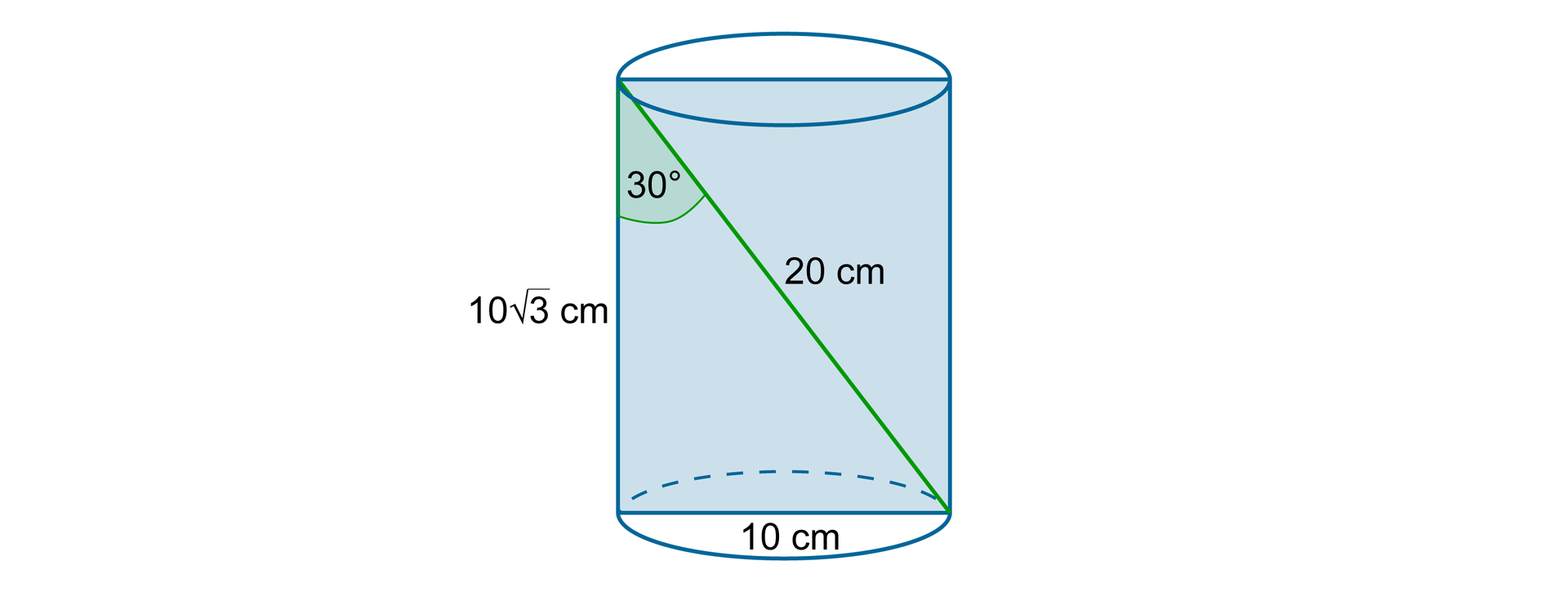
Rysunek walca z zaznaczonym przekrojem osiowym w kształcie prostokąta podzielonego przekątną na dwa trójkąty prostokątne. Przeciwprostokątna trójkąta ma długość 20 cm. Krótsza przyprostokątna leży naprzeciwko kąta o mierze 30 stopni i jest równa 10 cm a druga przyprostokątna ma długość 10 pierwiastków z trzech cm. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Promień podstawy walca jest więc równy $10 cm : 2 = 5 cm$ .
Obliczamy pole koła, będącego podstawą walca.

P = π \cdot 5^{2}

P = 25 π {cm}^{2}

Pole podstawy walca jest równe $25 π$ cmIndeks górny 2.

Przykład 10

Obwód przekroju poprzecznego walca jest równy $34 π {dm}^{2}$ . Stosunek wysokości walca do promienia podstawy jest równy $7 : 9$ . Oblicz wysokość walca.
Obliczamy promień $r$ podstawy walca.

2 πr = 34 π / : 2 π

r = 17 dm

Korzystamy z tego, że stosunek wysokości $H$ walca do promienia jego podstawy jest równy $7 : 9$ .

\frac{H}{r} = \frac{7}{9}

\frac{H}{17} = \frac{7}{9}

H = \frac{119}{9}

H = 13 \frac{2}{9} dm

Wysokość walca jest równa $13 \frac{2}{9}$ cm.

i9xorS27vT_d5e251

Siatka walca. Pole powierzchni walca

RBArzW7o4VWUf1

RFZ8Sqwf8pfjJ1

Przykład 11

Obserwuj, jak wraz ze zmianą wysokości i promienia podstawy walca, zmieniają się wymiary figur tworzących siatkę walca. Co zauważasz?

RSnhL9adCIxWY1

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DvaowsLHi

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY NC 3.0.

Siatka walca składa się z dwóch przystających kół i prostokąta. Promień każdego z tych kół jest równy promieniowi podstawy walca. Boki prostopadłe prostokąta są równe odpowiednio wysokości walca i obwodowi koła, będącego podstawą.

R14de92tKU1KS1

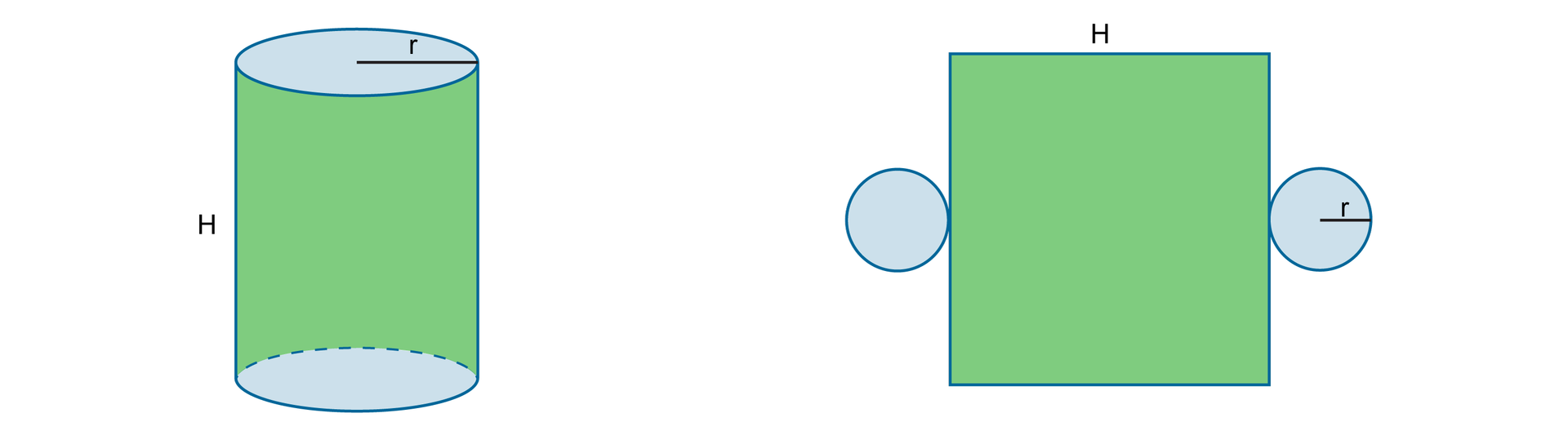
Rysunek walca i jego siatki o wysokości równej H i promieniu równym r. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ważne!

Pole $P$ powierzchni walca o wysokości $H$ i promieniu podstawy $r$ jest równe

P = 2 \cdot P_{p} + P_{b}

gdzie

$P_{p}$ - pole podstawy
$P_{b}$ - pole powierzchni bocznej.
$P = 2 π r^{2} + 2 πr \cdot H$

Przykład 12

Ile ${cm}^{2}$ blachy zużyto na wykonanie metalowej puszki w kształcie walca o wysokości $20 cm$ i średnicy $8 cm$ ? Wynik podaj z dokładnością do dwóch miejsc po przecinku.
Promień podstawy walca jest równy $8 cm : 2 = 4 cm$ . Obliczamy, ile blachy zużyto na wykonanie denka puszki.

P = π r^{2}

P_{p} = π \cdot 4^{2}

P_{p} = 16 π {cm}^{2}

Obliczamy, ile blachy użyto na wykonanie powierzchni bocznej puszki.

P_{b} = 2 π \cdot 4 \cdot 20

P_{b} = 160 π {cm}^{2}

Teraz obliczamy, ile blachy użyto na wykonanie całej puszki.

P = 2 \cdot 16 π + 160 π = 192 π

Liczbę $π$ zastępujemy jej przybliżeniem.

P \approx 192 \cdot 3,14 = 602,88

P \approx 602,88 {cm}^{2}

Na wykonanie puszki zużyto około 602, 88 cmIndeks górny 2 blachy.

Przykład 13

Powierzchnia boczna walca po rozwinięciu na płaszczyźnie jest prostokątem o wymiarach $15 cm x 24 cm$ . Oblicz promień podstawy walca, wiedząc, że wysokość walca jest równa $15 cm$ .
Obwód koła, który jest podstawą walca, jest równy długości prostokąta, w kształcie którego jest powierzchnia boczna walca.

2 πr = 24

r = \frac{24}{2 π} = \frac{12}{π}

Promień podstawy walca jest równy $\frac{12}{π} cm$ .

Przykład 14

Tort ma kształt walca o wysokości $25 cm$ i średnicy podstawy $30 cm$ . Na pokrycie $100 {cm}^{2}$ powierzchni tortu potrzeba $8 dag$ polewy. Oblicz, ile dag polewy należy przygotować na pokrycie powierzchni tortu.
Polewą będzie pokryta podstawa górna walca, w kształcie którego jest tort i jego powierzchnia boczna. Obliczamy pole powierzchni do pokrycia.

P = 2 π \cdot (\frac{30}{2}) 25 + π \cdot {(\frac{30}{2})}^{2}

P = 750 π + 225 π = 975 π

P \approx 975 \cdot 3,14 = 3061,5

P \approx 3061,5 {cm}^{2}

Obliczamy, ile dag polewy potrzeba.

(3061,5 : 100) \cdot 8 = 30,615 \cdot 8 = 244,92

Liczbę $π$ zaokrągliliśmy z dołu, zatem żeby nie zbrakło polewy, należy przygotować jej trochę więcej niż 244,92 dag.

i9xorS27vT_d5e421

Ćwiczenie 1

Kwadrat obracamy wokół prostej $p$ . Określ wysokość i promień podstawy tak otrzymanego walca.

RaMHFUxH6mrG21

Rysunki czterech kwadratów o osiach obrotu zawierających bok figury. Pierwszy kwadrat ma bok długości a. Drugi kwadrat ma bok długości 7. Trzeci kwadrat ma przekątną równą 3. Czwarty kwadrat ma przekątną równą a. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

$r = a, H = a$
$r = 7, H = 7$
$r = H = \frac{3 \sqrt{2}}{2}$
$r = \frac{a \sqrt{2}}{2}, H = \frac{a \sqrt{2}}{2}$

classicmobile

Ćwiczenie 2

Prostokąt o wymiarach $10 cm x 4 cm$ obracamy wokół dłuższego boku. Średnica podstawy tak otrzymanego walca jest równa

RSN8Q6Br6egzW

$10 cm$
$4 cm$
$20 cm$
$8 cm$

static

Ćwiczenie 2

Prostokąt o wymiarach $10 cm x 4 cm$ obracamy wokół dłuższego boku. Średnica podstawy tak otrzymanego walca jest równa

RmbeMZ2sKiT8W

$10 cm$
$4 cm$
$20 cm$
$8 cm$

Ćwiczenie 3

Uzupełnij zdania.

Przekrój osiowy walca jest kwadratem o polu $0,25 {dm}^{2}$ . Promień podstawy tego walca jest równy … $dm$ .
Przekrój osiowy walca jest kwadratem. Pole podstawy walca jest równe $81 π$ . Wysokość tego walca jest równa …
Przekrój osiowy walca jest kwadratem. Średnica podstawy walca jest równa $12 cm$ . Wysokość walca jest równa … $cm$ .

$0,25 dm$
$18$
$12 cm$

Ćwiczenie 4

Uzupełnij.

Tabela. Dane
Wysokość walca	Średnica podstawy walca	Pole przekroju osiowego	Pole przekroju płaszczyzną równoległą do podstawy	Długość przekątnej przekroju osiowego
$5$		$30 π$
			$16 π$	$10$
	$12$	$120$
$1,2$			$1,44 π$

Tabela. Dane
Wysokość walca	Średnica podstawy walca	Pole przekroju osiowego	Pole przekroju płaszczyzną równoległą do podstawy	Długość przekątnej przekroju osiowego
$5$	$6 π$	$30 π$	$9 π^{3}$	$\sqrt{25 + 36 π^{2}}$
$6$	$8$	$48$	$16 π$	$10$
$10$	$12$	$120$	$36 π$	$2 \sqrt{61}$
$1,2$	$2,4$	$2,88$	$1,44 π$	$3 \sqrt{0,8}$

Ćwiczenie 5

Rft9LAGt0pZsw1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

classicmobile

Ćwiczenie 6

Pole powierzchni całkowitej walca jest równe $748$ . Promień podstawy walca jest równy $7$ . Przyjmij $π = \frac{22}{7}$ . Wtedy wysokość walca jest równa

R18hUzoCYnHob

$49$
$7$
$10$
$8$

static

Ćwiczenie 6

Pole powierzchni całkowitej walca jest równe $748$ . Promień podstawy walca jest równy $7$ . Przyjmij $π = \frac{22}{7}$ . Wtedy wysokość walca jest równa

Rfv18QkGzulXj

$49$
$7$
$10$
$8$

Ćwiczenie 7

Powierzchnia boczna walca po rozwinięciu na płaszczyźnie jest prostokątem o wymiarach $10 dm x 12 dm$ . Oblicz pole powierzchni całkowitej walca. Rozważ dwa przypadki.

$(120 + \frac{72}{π}) {dm}^{2}$ lub $(120 + \frac{50}{π}) {dm}^{2}$

classicmobile

Ćwiczenie 8

Dany jest prostokąt o wymiarach $6 cm$ na $8 cm$ . W wyniku obrotu tego prostokąta wokół prostej, na której leży dłuższy bok, otrzymano walec $W$ , a w wyniku obrotu tego prostokąta wokół prostej, na której leży krótszy bok, otrzymano walec $W 1$ .
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

R1dvpNVHk71V3

Pole powierzchni bocznej walca $W$ jest większe od pola powierzchni bocznej walca $W 1$ .
Wysokość walca $W$ jest większa od wysokości walca $W 1$ .
Pole podstawy górnej walca $W$ jest równe polu podstawy dolnej walca $W 1$ .
Średnica podstawy walca $W$ jest mniejsza od średnicy podstawy walca $W 1$ .
Pola powierzchni całkowitej walca $W$ jest równe polu powierzchni całkowitej walca $W 1$ .
Pole przekroju osiowego walca $W$ jest większe od pola przekroju osiowego walca $W 1$ .

static

Ćwiczenie 8

R1Bv7kDxBEm6Q

Pole powierzchni bocznej walca $W$ jest większe od pola powierzchni bocznej walca $W 1$ .
Wysokość walca $W$ jest większa od wysokości walca $W 1$ .
Pole podstawy górnej walca $W$ jest równe polu podstawy dolnej walca $W 1$ .
Średnica podstawy walca $W$ jest mniejsza od średnicy podstawy walca $W 1$ .
Pola powierzchni całkowitej walca $W$ jest równe polu powierzchni całkowitej walca $W 1$ .
Pole przekroju osiowego walca $W$ jest większe od pola przekroju osiowego walca $W 1$ .

Ćwiczenie 9

Przekątna przekroju osiowego walca ma długość $4 \sqrt{2} cm$ . Przekątna ta tworzy kąt o mierze $45 °$ z jednym z boków prostokąta, będącego przekrojem osiowym walca. Oblicz pole powierzchni całkowitej walca.

$24 π {cm}^{2}$

Ćwiczenie 10

Kwadrat o boku długości $16 cm$ obrócono wokół jednego z boków. Oblicz pole powierzchni bocznej tak otrzymanego walca.

$512 π {cm}^{2}$ lub $25 π \sqrt{3} {cm}^{2}$

i9xorS27vT_d5e745

Ćwiczenie 11

Walec powstał w wyniku obrotu prostokąta wokół jednego z jego boków. Przekątna tego prostokąta ma długość $5 cm$ i jest nachylona do jego boku pod kątem $60 °$ . Oblicz pole powierzchni bocznej walca.

$\frac{25 π \sqrt{3}}{2} {cm}^{2}$

classicmobile

Ćwiczenie 12

Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

R1QaHemvO31Bi

Każdy przekrój poprzeczny walca jest kołem.
Tworzące walca mogą mieć różne długości.
Istnieje przekrój walca , który nie jest kołem ani prostokątem.

static

Ćwiczenie 13

Udowodnij, że wszystkie przekroje poprzeczne walca są przystającymi kołami.

Ćwiczenie 14

Prostokąt o wymiarach $a cm x b cm$ obrócono wokół boku o długości $a cm$ i otrzymano walec $W_{1}$ . Ten sam prostokąt obrócono wokół boku o długości $b cm$ i otrzymano walec $W_{2}$ . Walce $W_{1}$ i $W_{2}$ mają równe pola całkowite. Wykaż, że prostokąt ten jest kwadratem.

$2 πab + 2 π b^{2} = 2 πab + 2 π a^{2}$ , stąd $a = b$

Ćwiczenie 15

Dwa prostokąty $P_{1}$ i $P_{2}$ są podobne w skali $1 : 2$ . Prostokąt $P_{1}$ ma wymiary $5 cm x 10 cm$ . Oblicz pole powierzchni bocznej walca powstałego w wyniku obrotu prostokąta $P_{2}$ wokół dłuższego boku.

$400 π {cm}^{2}$

Ćwiczenie 16

Oblicz pole przekroju osiowego walca otrzymanego w wyniku obrotu prostokąta o wymiarach $20 cm x 5 cm$ wokół krótszego boku.

$200 {cm}^{2}$

Ćwiczenie 17

Przekątna przekroju osiowego walca ma długość $12 \sqrt{2}$ i tworzy z płaszczyzną podstawy walca kąt o mierze $45 ° .$ Oblicz pole powierzchni całkowitej walca.

$216 π {cm}^{2}$

Ćwiczenie 18

Udowodnij, że stosunek powierzchni bocznej dowolnego walca do powierzchni przekroju osiowego tego walca jest zawsze taki sam.

$π$

Ćwiczenie 19

Przekątna przekroju osiowego walca ma długość $10 cm$ , a wysokość walca $8 cm$ . Oblicz pole powierzchni otrzymanej po rozwinięciu tego walca na płaszczyźnie.

$66 π$

Ćwiczenie 20

Pole powierzchni całkowitej walca jest równe $216 π$ . Wysokość walca jest równa średnicy jego podstawy. Oblicz promień podstawy walca oraz jego wysokość.

$r = 6, H = 12$

Bryły obrotowe

Objętość walca

Walec. Pole powierzchni walca

Budowa walca

Przekroje walca

Siatka walca. Pole powierzchni walca