Własności podobieństwa

W tym materiale zawarte są informacje na temat własności podobieństwa. Poznasz podstawowe twierdzenia związane z tym tematem. Po przeanalizowaniu zadań, możesz sprawdzić swoje umiejętności, samodzielnie rozwiązując zadania powiązane z własnościami podobieństwa.

Twierdzenie: Własności podobieństwa

Jeżeli trójkąt $A' B' C'$ jest podobny do trójkąta $A B C$ w skali podobieństwa $k$ , to stosunek obwodów tych trójkątów jest równy skali podobieństwa, a stosunek ich pól jest równy kwadratowi skali podobieństwa

\frac{L_{A' B' C'}}{L_{A B C}} = k

\frac{P_{A' B' C'}}{P_{A B C}} = k^{2}

Rozważmy trójkąty prostokątne $A' B' C'$ oraz $A B C$ podobne w skali $k$ . Wysokości tych trójkątów zaznaczone na rysunku są równe odpowiednio $h'$ i $h$ .

R10R8XlTrU6Uv1

Rysunek trójkątów prostokątnych A B C o bokach długości a, b, c oraz A prim B prim C prim o bokach długości a prim, b prim, c prim. W trójkącie ABC wysokość AD równa jest h, a w trójkącie A prim B prim C prim wysokość A prim D prim jest równa h prim. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zauważmy, że skoro trójkąt $A' B' C'$ jest podobny do trójkąta $A B C$ , to

\frac{|C' A'|}{|C A|} = k

oraz

|∢ A C D| = |∢ A' C' D'|

|∢ C D A| = |∢ C' D' A'| = 90 °

Stąd

|∢ C A D| = |∢ C' A' D'| = 90 ° - |∢ A' C' D'|

Na mocy cechy podobieństwa kąt – bok – kąt trójkąt $A' C' D'$ jest podobny do trójkąta $A C D$ i skala podobieństwa wynosi $k$ . Stąd

\frac{h'}{h} = k

czyli stosunek długości wysokości w trójkątach podobnych jest taki sam jak stosunek długości boków.

P_{A' B' C'} = \frac{1}{2} c' h' = \frac{1}{2} k c \cdot k h = \frac{1}{2} c h \cdot k^{2} = P_{A B C} \cdot k^{2}

\frac{P_{A' B' C'}}{P_{A B C}} = k^{2}

Stosunek pól trójkątów podobnych jest więc równy kwadratowi skali podobieństwa.

L_{A' B' C'} = a' + b' + c' = k a + k b + k c = k (a + b + c) = k \cdot L_{A B C}

\frac{L_{A' B' C'}}{L_{A B C}} = k

Stosunek obwodów trójkątów podobnych jest równy skali podobieństwa.

Rozważmy dowolny trójkąt $A B C$ . Zaznaczmy w nim środki dwóch boków i połączmy je odcinkiem. Taki odcinek nazywamy linią środkową trójkąta.

Rptb5di8U4qZC1

Rysunek trójkąta A B C z zaznaczoną linią środkową D E, która jest równoległa do boku A B. Punkty D i E leżą odpowiednio na środkach boków A C i B C. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zauważmy, że trójkąty $D C E$ i $A B C$ są podobne na mocy cechy bok – kąt – bok. Kąt $D C E$ jest wspólny dla obu trójkątów oraz

\frac{|D C|}{|A C|} = \frac{|E C|}{|B C|} = \frac{1}{2}

Z definicji podobieństwa wynika, że $\frac{|D E|}{|A B|} = \frac{1}{2}$ . Mamy też równość kątów

|∢ C D E| = |∢ C A B|

|∢ C E D| = |∢ C B A|

Ponieważ punkty $C$ , $D$ , $A$ są współliniowe, więc kąty $C D E$ i $C A B$ są odpowiadające. Stąd wynika równoległość $D E$ i $A B$ .

RxiBthI3j6aGF1

Rysunek trójkąta A B C z zaznaczoną linią środkową D E, równoległą do boku A B. Długość boku A B oznaczono 2 z, odcinek D E ma długość z. Punkt D dzieli bok AC na dwa równe odcinki o długości x, a punkt E dzieli bok B C na dwa równe odcinki o długości y. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

o linii środkowej trójkąta1

Twierdzenie: o linii środkowej trójkąta

Odcinek łączący środki dwóch boków w trójkącie jest równoległy do trzeciego boku trójkąta i jest od niego dwa razy krótszy.

RmC1zjyXQlthQ1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Podstawy trapezu $A B C D$ mają długości $a$ oraz $b$ . Punkt $E$ jest środkiem boku $A D$ , a punkt $F$ jest środkiem boku $C B$ . Odcinek łączący środki ramion trapezu nazywamy linią środkową w trapezie. Obliczymy jego długość.

RVNPLakZj2xKf1

Rysunek trapezu A B C D z zaznaczoną linią środkową E F równoległą do podstaw A B i C D. Dłuższa podstawa A B ma długość b, a krótsza podstawa C D ma długość a. Punkty E leży w połowie długości ramienia A D, a punkt F leży w połowie długości ramienia B C. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Poprowadźmy przekątną $A C$ i oznaczmy przez $G$ jej środek.

R1SniulANaFdJ1

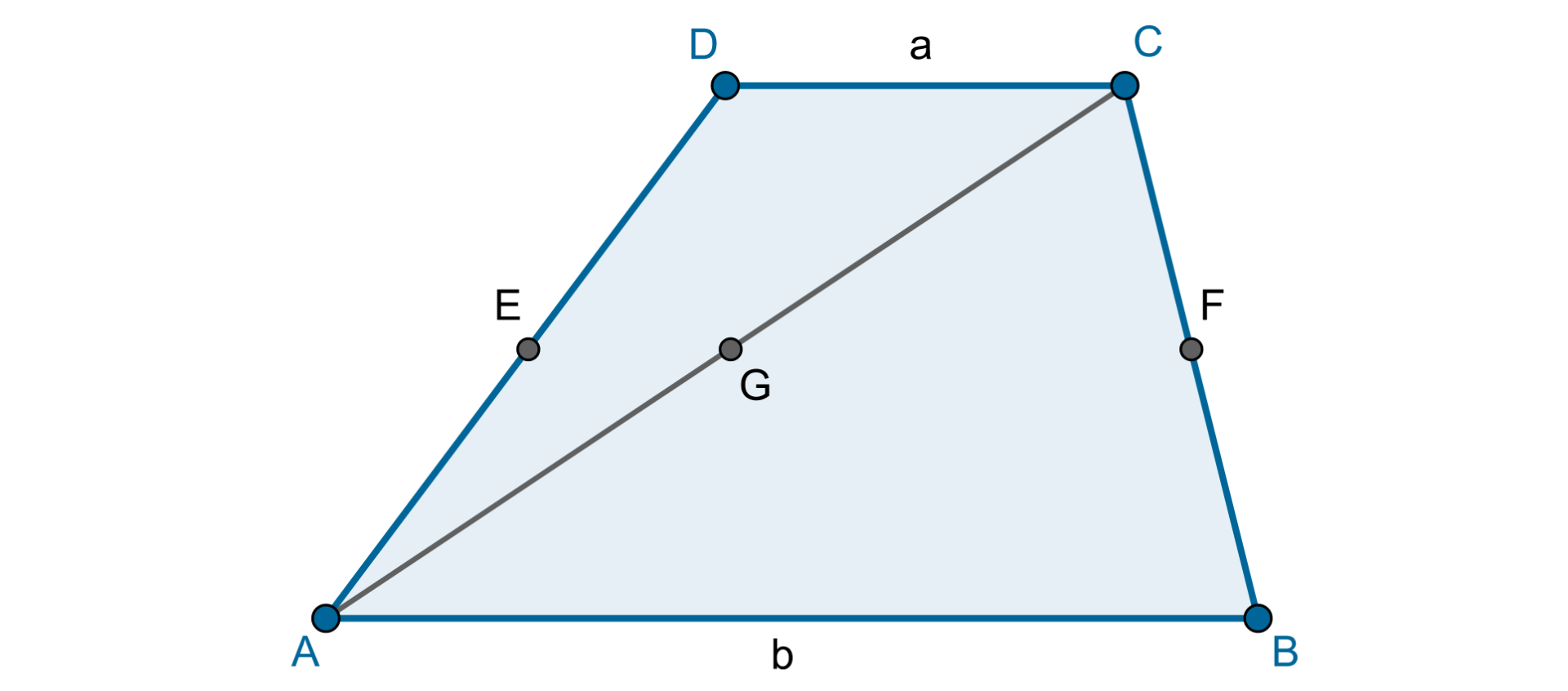
Rysunek trapezu A B C D. Dłuższa podstawa A B ma długość b, a krótsza podstawa C D ma długość a. Punkty E leży w połowie długości ramienia AD, a punkt F leży w połowie długości ramienia BC. Poprowadzono przekątną A C tego trapezu, a w połowie jej długości umieszczono punkt G. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Odcinek $E G$ jest odcinkiem łączącym środki boków w trójkącie $A D C$ . Stąd $E G$ jest równoległy do podstawy trapezu $D C$ oraz

|E G| = \frac{1}{2} a

Podobnie odcinek $G F$ jest odcinkiem łączącym środki boków trójkąta $A B C$ , czyli jest równoległy do podstawy trapezu $A B$ oraz

|G F| = \frac{1}{2} b

Ponieważ oba odcinki $E G$ i $G F$ są równoległe do podstaw trapezu, więc punkty $E$ , $G$ , $F$ leżą na jednej prostej.

R1LlMMAlvwhtk1

Rysunek trapezu A B C D z zaznaczoną linią środkową E F oraz przekątną A C. Dłuższa podstawa A B ma długość b, a krótsza podstawa C D ma długość a. Punkty E leży w połowie długości ramienia A D, a punkt F leży w połowie długości ramienia B C. W połowie długości przekątnej A C umieszczono punkt G. Widać, że punkt G jest punktem przecięcia przekątnej A C i środkowej E F. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Mamy

|E F| = |E G| + |G F| = \frac{1}{2} a + \frac{1}{2} b = \frac{a + b}{2}

Stąd twierdzenie:

o linii środkowej w trapezie1

Twierdzenie: o linii środkowej w trapezie

Odcinek łączący środki ramion trapezu jest równoległy do podstaw tego trapezu, a jego długość jest równa średniej arytmetycznej długości podstaw trapezu.

RSmne8jrHRayc1

Ćwiczenie 1

Punkty $K$ , $L$ i $M$ dzielą ramię $A C$ trójkąta $A B C$ na odcinki równej długości. Punkty $N$ , $O$ i $P$ wybrano na boku $B C$ tak, że odcinki $M N$ , $L O$ i $K P$ są równoległe do podstawy $A B$ (patrz rysunek). Długość odcinka $M N$ jest równa $2$ .

R1bsWl9qb8PNk1

Rysunek trójkąta A B C z zaznaczonymi odcinkami: K P, L O, M N równoległymi do podstawy A B. Punkty M, L, K leżą na ramieniu A C, a punkty N, O, P leżą na ramieniu B C trójkąta. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RCdyDlHwwu8QN

$"|"LO"|" = 4$
$"|"KP"|" = 8$
$\frac{P_{CMN}}{P_{ABC}} = \frac{1}{16}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 2

Ri2GmPAab0ZTO

Trójkąt $SDC$ jest podobny do trójkąta $SAB$ w skali $\frac{3}{5}$ .
Długość odcinka $SC$ jest równa $18$ .
$\frac{P_{SAB}}{P_{SDC}} = \frac{9}{25}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 3

R1QJp9EnOFjjM

Uzupełnij odpowiedzi, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. W trapezie

A B C D

podstawa

A B

jest dłuższa od podstawy

C D

. Punkt przecięcia przekątnych trapezu dzieli każdą z nich w stosunku

2 : 3

. Krótsza podstawa trapezu ma długość

5

. Ile wynosi długość drugiej podstawy?
Odpowiedź:

|A B| =

\frac{3}{7}

, 2.

5, 5

, 3.

6, 5

, 4.

\frac{4}{5}

, 5.

7, 5

, 6.

26

, 7.

24

, 8.

\frac{5}{8}

, 9.

28

W trapezie

A B C D

podstawy mają długości

|A B| = 9

|C D| = 3

. Przekątna

B D

ma długość

8

. Na jakie odcinki dzieli tę przekątną prosta

A C

?
Odpowiedź: Dzieli na odcinki o długości 1.

\frac{3}{7}

, 2.

5, 5

, 3.

6, 5

, 4.

\frac{4}{5}

, 5.

7, 5

, 6.

26

, 7.

24

, 8.

\frac{5}{8}

, 9.

28

.
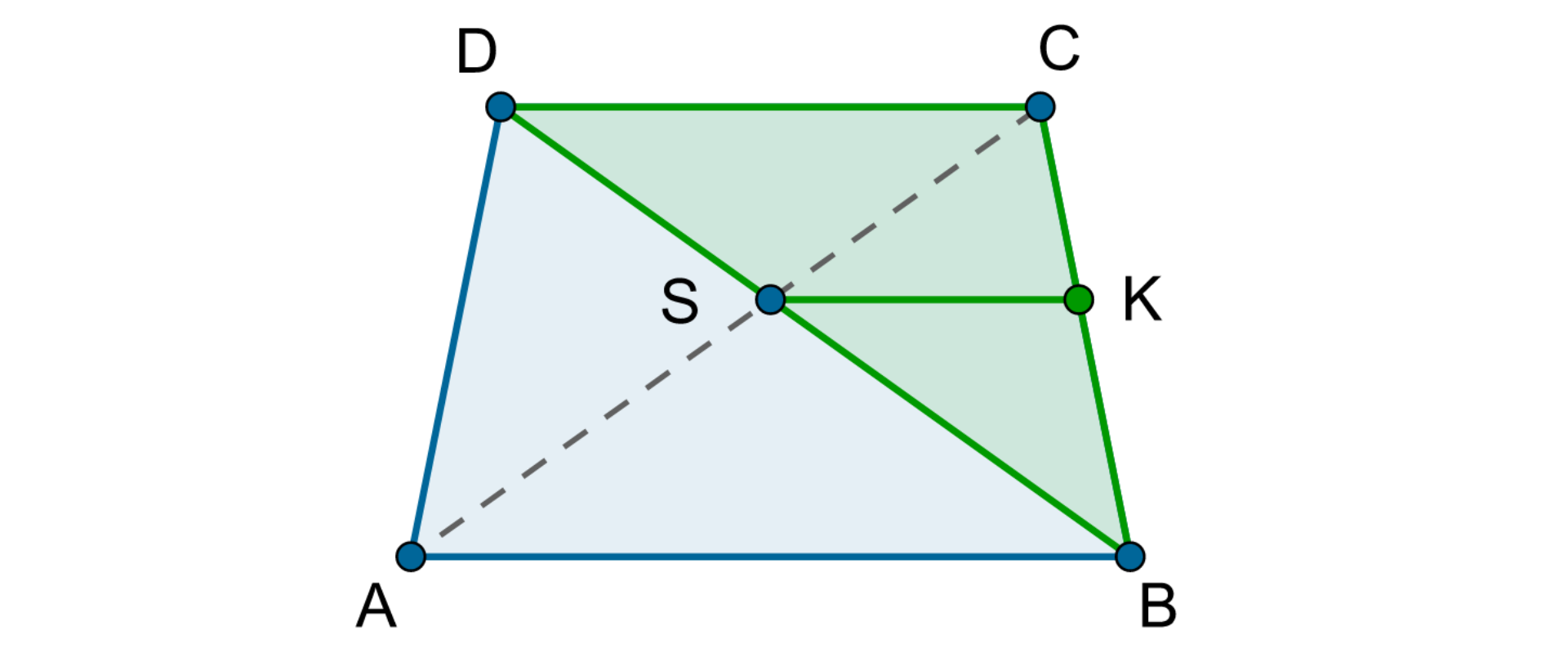
W trapezie

A B C D

podstawy mają długości

|A B| = 8

|C D| = 2

. Przekątne

A C

B D

przecinają się w punkcie

S

. Trójkąt

S A B

ma pole równe

10

. Oblicz pole trójkąta

S C D

.
Odpowiedź:

P_{S C D} =

\frac{3}{7}

, 2.

5, 5

, 3.

6, 5

, 4.

\frac{4}{5}

, 5.

7, 5

, 6.

26

, 7.

24

, 8.

\frac{5}{8}

, 9.

28

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RNbqPjwOmJYUk1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Trójkąt $S D C$ jest podobny do trójkąta $S B A$ , ponieważ odpowiednie kąty (zaznaczone na rysunku kolorami) są wierzchołkowe albo naprzemianległe, czyli równe. Otrzymujemy więc równanie

\frac{2 x}{3 x} = \frac{5}{|A B|}

|A B| = 7, 5

R1akFRC7MJyN41

Rysunek trapezu A B C D - pomocniczy do rozwiązania podpunktu drugiego. Podstawy trapezu mają długość A B =9 i C D =3 . Poprowadzone przekątne trapezu A C i D B przecinają się w punkcie S. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Trójkąt $S D C$ jest podobny do trójkąta $S B A$ (patrz podpunkt $1$ )).Mamy więc $\frac{3}{9} = \frac{|D S|}{|S B|}$ oraz $|D S| + |S B| = 8$ . Stąd

\frac{1}{3} = \frac{|D S|}{8 - |D S|}

3 |D S| = 8 - |D S|

4 |D S| = 8

|D S| = 2

|S B| = 8 - 2 = 6

Trójkąt $S D C$ jest podobny do trójkąta $S B A$ , a skala tego podobieństwa jest równa $k = \frac{2}{8} = \frac{1}{4}$ . Mamy więc

\frac{P_{S D C}}{P_{S B A}} = {(\frac{1}{4})}^{2} = \frac{1}{16}

P_{S D C} = \frac{1}{16} P_{S B A} = \frac{1}{16} \cdot 10 = \frac{5}{8}

R1Y3YKkS74PYv1

Ćwiczenie 4

W trójkącie prostokątnym przyprostokątne mają długości $3$ i $6$ . Wtedy wysokość poprowadzona z wierzchołka kąta prostego dzieli przeciwprostokątną na odcinki długości $\sqrt{5}$ i $2 \sqrt{5}$ .
W trójkącie prostokątnym $ABC$ stosunek długości przyprostokątnych $AB$ i $AC$ jest równy 15:8. Poprowadzono wysokość $AD$ . Pole trójkąta $ACD$ jest równe $16$ . Wtedy pole trójkąta $ABC$ jest równe $72,25$ .
W trójkącie prostokątnym o przyprostokątnych długości $a$ i $b$ wysokość poprowadzona z wierzchołka kąta prostego jest równa $\frac{ab}{\sqrt{a^{2} + b^{2}}}$ .

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rxa5etx3TDmll1

Ćwiczenie 5

Odcinki $"|"AD"|" = 6$ i $"|"BE"|" = 7$ są wysokościami trójkąta ostrokątnego $ABC$ , którego bok $BC$ ma długość $8$ . Wtedy, $"|"AC"|" = \frac{28}{3}$ .
Trójkąt $ABC$ jest równoramienny o ramionach długości $25$ i podstawie długości $30$ . Wtedy wysokości w tym trójkącie są równe $20$ i $24$ .

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 6

Zapoznaj się z poniższymi poleceniami i wykonaj odpowiednie obliczenia.

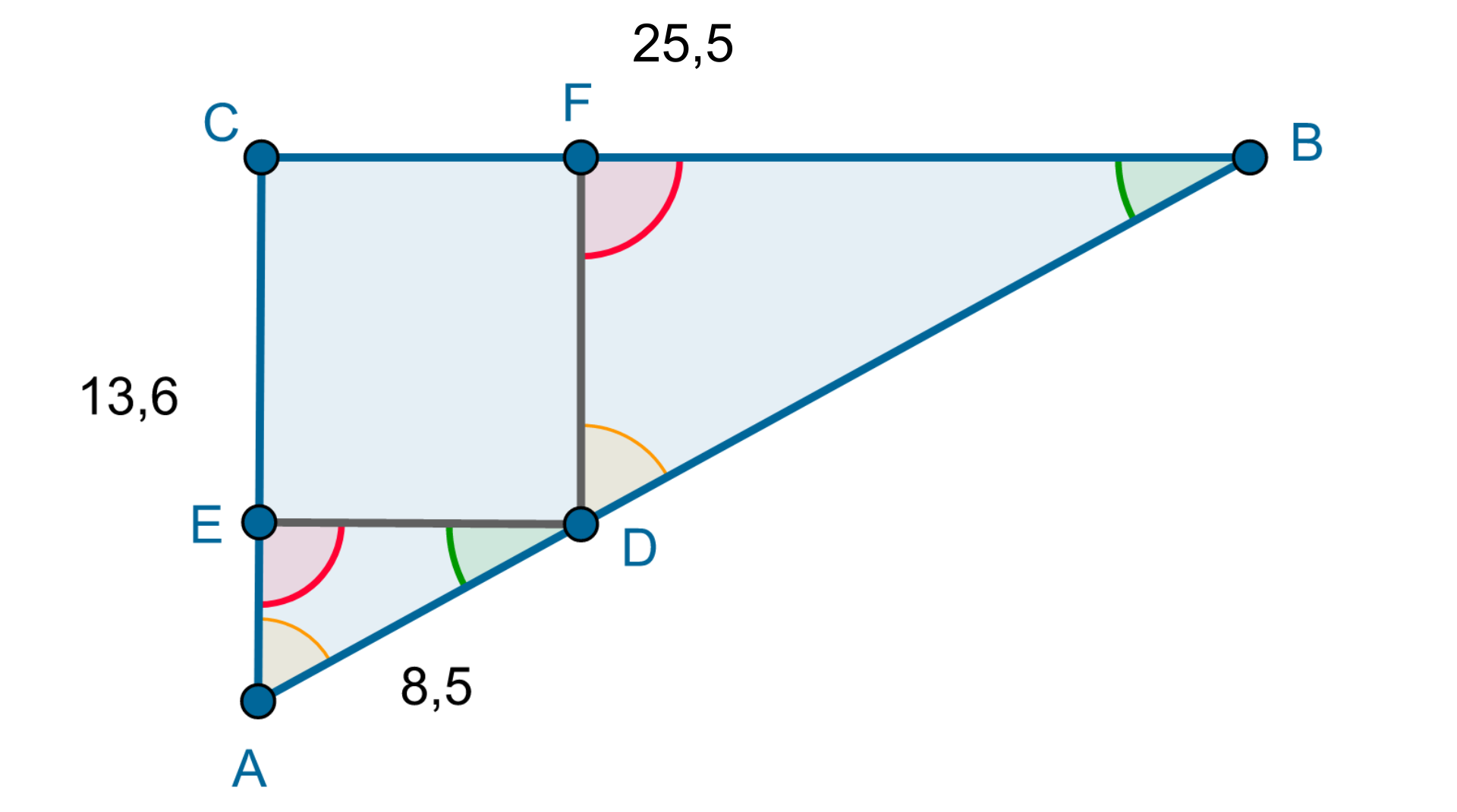
W trójkąt prostokątny $A B C$ o przyprostokątnych $|A B| = 4$ i $|A C| = 7$ wpisano kwadrat, tak jak na rysunku. Oblicz długość boku tego kwadratu.
RR4qDhnb9H5JT1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
W trójkąt $A B C$ o podstawie $|A B| = 40$ i wysokości równej $16$ opuszczonej z wierzchołka $C$ na tę podstawę wpisano prostokąt, tak jak na rysunku. Długości odcinków $E F$ i $D E$ pozostają w stosunku $2 : 5$ . Znajdź długości boków prostokąta $D E F G$ .
R1VWP6o3tyNKY1
Rysunek trójkąta A B C opisanego w zadaniu w podpunkcie b, z wpisanym prostokątem D E F G o bokach długości 5x i 2x. Bok DE prostokąta leży w całości na boku AB trójkąta, wierzchołek G tego prostokąta leży na boku AC trójkąta, a wierzchołek F tego prostokąta leży na boku BC tego trójkąta. W trójkącie poprowadzona jest wysokość z punktu S opadająca na podstawę AB o długości szesnaście.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
W trójkąt prostokątny $A B C$ , w którym kąt $A C B$ jest prosty, wpisano kwadrat $D E G F$ o boku długości $4$ . Bok $G F$ kwadratu leży na przeciwprostokątnej $A B$ trójkąta. Wierzchołki $E$ , $D$ leżą odpowiednio na przyprostokątnych $A C$ i $C B$ . Odcinek $A G$ jest równy $2$ . Oblicz pole trójkąta $A B C$ .
RTse8t7kcCXHq1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RUIYKOQ0KZGN1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Trójkąt $C E F$ jest podobny do trójkąta $C A B$ na mocy cechy podobieństwa kąt – kąt – kąt, ponieważ trójkąty mają wspólny kąt przy wierzchołku $C$ oraz oba są prostokątne. Kąt odpowiedni w obu trójkątach jest więc równy. Zachodzi więc równość
$\frac{|C E|}{|C A|} = \frac{x}{|A B|}$
$\frac{7 - x}{7} = \frac{x}{4}$
$28 - 4 x = 7 x$
$11 x = 28$
$x = \frac{28}{11}$ .
Prosta $G F$ jest równoległa do $A B$ , stąd odpowiednie kąty (patrz rysunek) są równe, jako kąty odpowiadające. Trójkąt $C G F$ jest podobny do trójkąta $C A B$ na mocy cechy podobieństwa kąt – kąt – kąt.
R9SufbuUkikYs1
Rysunek trójkąta A B C opisanego w zadaniu w podpunkcie b, z wpisanym prostokątem D E F G o bokach długości 5x i 2x. Bok DE prostokąta leży w całości na boku AB trójkąta, wierzchołek G tego prostokąta leży na boku AC trójkąta, a wierzchołek F tego prostokąta leży na boku BC tego trójkąta. W trójkącie poprowadzona jest wysokość z punktu S opadająca na podstawę AB o długości szesnaście. W trójkącie zaznaczono pary kątów o takich samych miarach: BAC i FGC, CFG i CBA.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Przez $2 x$ oznaczmy długość odcinka $E F$ . Wówczas odcinek $D E$ ma długość $5 x$ .Stosunek długości odpowiednich wysokości w trójkątach podobnych jest równy skali podobieństwa, czyli jest równy stosunkowi długości odpowiednich boków. Stąd otrzymujemy
$\frac{16 - 2 x}{16} = \frac{5 x}{40}$
$\frac{8 - x}{8} = \frac{x}{8}$
$8 - x = x$
$x = 4$ .
Długości boków prostokąta $D E F G$ są równe $2 x = 8$ , oraz $5 x = 20$ .
Zauważmy, że otrzymane trójkąty są do siebie podobne oraz podobne do całego trójkąta $A B C$ .
R1dNFeUQwV2T91
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Z podobieństwa trójkątów $A G E$ oraz $D F B$ obliczamy długość odcinka $B F$ . $\frac{|A G|}{|D F|} = \frac{|E G|}{|F B|}$ , czyli $\frac{2}{4} = \frac{4}{|F B|}$ , skąd $|F B| = 8$ . Długość przeciwprostokątnej trójkąta $A B C$ jest więc równa $14$ . Długość przeciwprostokątnej $A E$ w trójkącie $A G E$ obliczymy z twierdzenia Pitagorasa
${|A E|}^{2} = 2^{2} + 4^{2} = 20$ .
Ponieważ $|A E| > 0$ , to
$|A E| = 2 \sqrt{5}$ .
Skala podobieństwa trójkąta $A G E$ do trójkąta $A C B$ jest więc równa
$k = \frac{2 \sqrt{5}}{14} = \frac{\sqrt{5}}{7}$ .
Pole trójkąta $A G E$ jest równe $P_{A G E} = 4$ . Stosunek pól trójkątów podobnych jest równy kwadratowi skali podobieństwa, czyli
$\frac{P_{A G E}}{P_{A C B}} = \frac{5}{49} = \frac{4}{P_{A C B}}$ .
Otrzymujemy więc
$P_{A C B} = \frac{196}{5} = 39, 2$ .

Ćwiczenie 7

Zapoznaj się z poniższymi poleceniami i wykonaj odpowiednie obliczenia.

W trapezie $A B C D$ długość podstawy $A B$ jest równa $28$ , a długości ramion trapezu $A D$ i $B C$ są odpowiednio równe $20$ i $15$ . Kąty $A D B$ i $D C B$ , zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
R1VoCltSmZpfk1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Dwa trójkąty podobne $A B C$ i $B D E$ umieszczono obok siebie (patrz rysunek) tak, że punkty $A$ , $B$ i $D$ leżą na jednej prostej. Punkty $K$ , $L$ i $M$ są odpowiednio środkami odcinków $A B$ , $B D$ i $C E$ . Udowodnij, że trójkąt $K L M$ jest podobny do każdego z trójkątów $A B C$ i $B D E$ .
R1dVDwAT46J0k1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Przekątne czworokąta $A B C D$ przecinają się w punkcie $S$ i zachodzi równość $|A S| \cdot |D S| = |B S| \cdot |C S|$ . Udowodnij, że czworokąt $A B C D$ jest trapezem.

RGY5SZ7PCMqu4

Rysunek czworokąta A B C D opisanego w podpunkcie c. Poprowadzono w nim przekątne A C i B D, które przecinają się w punkcie S. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RcIWjXfqUgMYi

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wykorzystaj kąty naprzemianległe, aby wykazać podobieństwo trójkątów $C B D$ i $D B A$ . Interesujące Cię boki będziesz wtedy w stanie wyznaczyć korzystając z podobieństwa obu figur.
Wykorzystaj podobieństwo obu trójkątów do wyznaczenia odpowiednich kątów. Zwróć uwagę na to, że odcinek $K M$ jest środkową trapezu $A C E B$ .
Wykorzystaj równość podaną w zadaniu i fakt, że kąty DSC i ASB są wierzchołowe do wykazania, że trójkąty $A B S$ i $C D S$ są podobne. Następnie w oparciu o uzyskane dane wykaż równoległość boków $C D$ i $A B$ .

$|∢ C D B| = |∢ D B A|$ , gdyż są to kąty naprzemianległe. Stąd na mocy cechy podobieństwa kąt – kąt – kąt trójkąt $A B D$ jest podobny do trójkąta $B C D$ .
RdFrK74BHynUy1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Z podobieństwa tych trójkątów otrzymujemy
$\frac{20}{15} = \frac{28}{|D B|} = \frac{|D B|}{|D C|}$ .
Stąd
$|D B| = \frac{15 \cdot 28}{20} = 21$
$\frac{|D C|}{|D B|} = \frac{|D B|}{|A B|}$
$|D C| = \frac{21^{2}}{28} = 15, 75$ .
Obwód trapezu jest równy
$L = 20 + 28 + 15 + 15, 75 = 78, 75$ .
Ponieważ trójkąty $A B C$ i $B D E$ są podobne, więc $|∢ C A B| = |∢ E B D|$ . Punkty $A$ , $B$ i $D$ leżą na jednej prostej. Otrzymaliśmy więc dwa kąty odpowiadające równej miary. Stąd $A C$ jest równoległe do $B E$ . Figura $A B E C$ jest więc trapezem. Odcinek $K M$ łączy środki jego ramion, jest więc równoległy do podstaw $A C$ oraz $B E$ , zatem
$|∢ C A B| = |∢ M K B| = |∢ E B D|$ .
Podobnie można wykazać, że figura $C B D E$ jest trapezem. Odcinek $M L$ łączy środki jego ramion, zatem jest równoległy do podstaw $C B$ i $D E$ trapezu $C B D E$ . Stąd
$|∢ C B A| = |∢ M L A| = |∢ E D A|$ .
Z cechy podobieństwa kąt – kąt – kąt wynika, że trójkąty $K L M$ , $A B C$ , $B D E$ są podobne.
Rm3TcuwzEs35V1
Animacja pokazuje w dziewięciu krokach ilustrację rozwiązania zadania podpunkt b. W pierwszym kroku przedstawione są dwa dane trójkąty: A B C i B D E. W drugim kroku wyszczególniono, że kąt C A B ma taką samą miarę jak kąt E B D. W trzecim kroku zaznaczono odcinek C E i środki odcinków A B, B D i C E, które oznaczono odpowiednio jako K, L i M. W kroku czwartym pokazano, że czworokąt A B E C jest trapezem o podstawach A C i B E. W piątym kroku poprowadzono odcinek K M równoległy do A C i B E. W kroku szóstym wyróżniono, że kąt A B C ma taką samą miarę jak kąt B D E. W kroku siódmym pokazano, że czworokąt C B D E jest trapezem i poprowadzono odcinek LM. W kroku ósmym pokazano, że bok LM jest równoległy do boków BC i DE. W ostatnim kroku możemy zauważyć, że trójkąt K L M ma takie same kąty jak trójkąty A B C i B D E. Oznacza to, że te trójkąty są podobne z cechy podobieństwa kąt - kąt - kąt.
Animacja pokazuje w dziewięciu krokach ilustrację rozwiązania zadania podpunkt b. W pierwszym kroku przedstawione są dwa dane trójkąty: A B C i B D E. W drugim kroku wyszczególniono, że kąt C A B ma taką samą miarę jak kąt E B D. W trzecim kroku zaznaczono odcinek C E i środki odcinków A B, B D i C E, które oznaczono odpowiednio jako K, L i M. W kroku czwartym pokazano, że czworokąt A B E C jest trapezem o podstawach A C i B E. W piątym kroku poprowadzono odcinek K M równoległy do A C i B E. W kroku szóstym wyróżniono, że kąt A B C ma taką samą miarę jak kąt B D E. W kroku siódmym pokazano, że czworokąt C B D E jest trapezem i poprowadzono odcinek LM. W kroku ósmym pokazano, że bok LM jest równoległy do boków BC i DE. W ostatnim kroku możemy zauważyć, że trójkąt K L M ma takie same kąty jak trójkąty A B C i B D E. Oznacza to, że te trójkąty są podobne z cechy podobieństwa kąt - kąt - kąt.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PqPJuvlx4

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Przekształćmy równość daną w zadaniu do postaci $\frac{|A S|}{|C S|} = \frac{|B S|}{|D S|}$ . Zauważmy, że miara kąta $D S C$ jest równa mierze kąta $A S B$ , ponieważ są to kąty wierzchołkowe. Zatem trójkąty $A B S$ i $C D S$ są podobne, co wynika z cechy podobieństwa trójkątów bok – kąt – bok. Wynika stąd, że
$|∢ C D S| = |∢ S B A|$ .
Są to kąty naprzemianległe i równe, zatem bok $C D$ jest równoległy do $A B$ . Czworokąt $A B C D$ jest więc trapezem.

RXLA3oHK6fpOV2

Ćwiczenie 8

Stosunek długości przekątnych dwóch prostokątów podobnych jest równy $4 : 7$ . Wówczas stosunek pól tych prostokątów jest równy $4 : 7$ .
Stosunek pól dwóch trójkątów podobnych wynosi $144 : 225$ . Wówczas stosunek obwodów tych trójkątów jest równy $12 : 15$ .
W trójkącie $ABC$ poprowadzono odcinek $DE$ równoległy do podstawy $AB$ , który ramię $CB$ podzielił w stosunku $1 : 4$ , licząc od wierzchołka $C$ . Wówczas pole trójkąta $DEC$ stanowi $\frac{1}{16}$ pola trójkąta $ABC$ .

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1BUNjwzQTjmp2

Ćwiczenie 9

Ramiona trapezu mają długości $3$ i $5$ , a obwód trapezu jest równy $20$ . Wtedy długość odcinka łączącego środki ramion tego trapezu jest równa $12$ .
Wysokość trapezu jest równa $4$ , a odcinek łączący środki ramion trapezu ma długość $5$ . Wtedy pole tego trapezu jest równe $20$ .
W trapezie o podstawach długości $a$ i $b$ (gdzie $b > a$ ) odcinek łączący środki przekątnych ma długość $\frac{b - a}{2}$ .

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 10

Zapoznaj się z trójkątem na poniższej grafice. Odcinki $D E$ i $B C$ są równoległe oraz $|D B| = 8$ , $|D E| = 12$ , $|B C| = 16$ .

RKRwlXA7p9kx41

Rysunek trójkąta A B C. Na boku A B zaznaczono punkt D, a na boku A C zaznaczono punkt E. Odcinek D E ma długość 12, odcinek BC ma długość 16, a odcinek B D ma długość 8 — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1CMrGguxVBfl

$4$
$8$
$12$
$24$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RuDveXzYpfKUx2

Ćwiczenie 11

$1 : 1$
$1 : 2$
$1 : 3$
$1 : 4$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R13TNqUVIVfig2

Ćwiczenie 12

$7,5$
$4,8$
$\frac{40}{3}$
$4 \sqrt{3}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1X1yCt6TOhSz2

Ćwiczenie 13

$\frac{1}{2}$
$\frac{1}{3}$
$\frac{2}{3}$
$\frac{2}{3}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R4VKOYrXir0Ap2

Ćwiczenie 14

$8 m$
$9 m$
$12 m$
$18 m$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1QJZOK8S6R0a2

Ćwiczenie 15

$6$
$10$
$14$
$16$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 16

W trójkąt równoboczny o boku długości $4$ wpisano kwadrat, w taki sposób, że jego dwa wierzchołki leżą na jednym z boków trójkąta, a dwa pozostałe wierzchołki leżą na pozostałych dwóch ramionach trójkąta.

R1IoAFEIbbvZn1

Rysunek trójkąta równobocznego A B C o boku długości 4 z wpisanym wewnątrz kwadratem F G H I opisanym w zadaniu. Bok FG kwadratu całkowicie w całości leży na podstawie AB trójkąta. Wierzchołek I kwadratu leży na boku AC trójkąta, a wierzchołek H leży na boku BC trójkąta. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R13eue3N3MXgB

$8 \sqrt{3} - 12$
$4 \sqrt{3} - 6$
$\frac{\sqrt{3}}{2}$
$2 \sqrt{3}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R6HSi3vtrDl222

Ćwiczenie 17

$\frac{156}{5}$
$\frac{156}{10}$
$\frac{60}{13}$
$\frac{120}{13}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1Lo9mK02NvR52

Ćwiczenie 18

$10$
$22 \frac{1}{2}$
$33 \frac{3}{4}$
$40$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RPGss9gogA9p52

Ćwiczenie 19

$8$ i $12$
$6$ i $14$
$2$ i $18$
$4$ i $16$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 20

R1Iiid0b9a9dZ

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RLa1CnUSCORvK1

Rysunek trójkąta ABC - pomocniczy do rozwiązania zadania. Bok AC podzielono na dwa odcinki AD =2x i DC =x. Bok BC podzielono na dwa odcinki BE =2y i EC =y. Cały bok AC ma długość 6, cały bok BC ma długość 9 i cały bok AB ma długość dwanaście. Odcinek DE jest równoległy do podstawy AB trójkąta. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Trójkąty $C D E$ i $C A B$ mają wspólny kąt $D C E$ oraz boki przy tym kącie są proporcjonalne

\frac{|C D|}{|C A|} = \frac{x}{3 x} = \frac{1}{3}

\frac{|C E|}{|C B|} = \frac{y}{3 y} = \frac{1}{3}

Zatem trójkąty $C D E$ i $C A B$ są podobne, co wynika z cechy podobieństwa bok – kąt – bok. Skala tego podobieństwa jest równa $\frac{1}{3}$ .
Boki trójkąta $D E C$ są więc równe

|C E| = \frac{1}{3} \cdot 9 = 3

|C D| = \frac{1}{3} \cdot 6 = 2

|D E| = \frac{1}{3} \cdot 12 = 4

Ostatecznie obwód trójkąta $D E C$ jest równy

L_{D E C} = 3 + 2 + 4 = 9

Ćwiczenie 21

R1dPfy48VQgMk

Punkty

D

E

leżą na boku

A C

trójkąta

A B C

i dzielą go w stosunku

1 : 2 : 3

, licząc od wierzchołka

C

. Przez punkty

D

E

poprowadzono proste równoległe do boku

A B

. Oblicz, w jakim stosunku pozostają pola figur, na jakie te proste podzieliły trójkąt

A B C

. Uzupełnij odpowiedź, przeciągając w lukę odpowiednią liczbę lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.
Odpowiedź: Stosunek pola figur, na jakie te proste podzieliły trójkąt

A B C

wynoszą 1.

3 : 5 : 24

, 2.

2 : 6 : 25

, 3.

1 : 6 : 28

, 4.

1 : 8 : 27

, 5.

1 : 4 : 24

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1dm7zqxgrW2u1

Rysunek trójkąta A B C - pomocniczy do rozwiązania zadania. Bok CA podzielono na trzy odcinki CD =x, DE =2x i EA =3x. Punkty F, G leżą na boku BC. Odcinki DF i EG są równoległe do boku AB. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Pole trapezu $D E G F$ obliczymy jako różnicę pól trójkątów $C E G$ i $C D F$ .
Trójkąt $C D F$ jest podobny do trójkąta $C E G$ (na mocy cechy podobieństwa kąt – kąt – kąt) oraz $k = \frac{x}{3 x} = \frac{1}{3}$ . Stosunek pól tych trójkątów jest równy kwadratowi skali podobieństwa

\frac{P_{C D F}}{P_{C E G}} = \frac{1}{9}

Stąd

P_{C E G} = 9 P_{C D F}

a zatem

P_{D E G F} = 9 P_{C D F} - P_{C D F} = 8 P_{C D F}

Pole trapezu $E A B G$ obliczymy jako różnicę pól trójkątów $C A B$ i $C E G$ .
Trójkąt $C D F$ jest podobny do trójkąta $C A B$ (na mocy cechy podobieństwa kąt – kąt – kąt) oraz $k = \frac{x}{6 x} = \frac{1}{6}$ . Stosunek pól tych trójkątów jest równy kwadratowi skali podobieństwa

\frac{P_{C D F}}{P_{C A B}} = \frac{1}{36}

Stąd

P_{C E G} = 36 P_{C D F}

a zatem

P_{E A B G} = 36 P_{C D F} - 9 P_{C D F} = 27 P_{C D F}

Ćwiczenie 22

R14ibo9bJAa1g

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RPLZ23IrNZSUm1

Rysunek trapezu A B C D opisanego w zadaniu. Przedłużone ramiona AD i BC przecinają się w punkcie S. Długość odcinka AB to 18, długość odcinka DC to 6, długość odcinka DS to 3 i długość odcinka CS to pięć. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Trójkąty $S D C$ oraz $S A B$ są podobne na mocy cechy podobieństwa kąt – kąt – kąt. Otrzymujemy równanie

\frac{|S D|}{|S D| + |D A|} = \frac{|D C|}{|A B|}

\frac{3}{3 + |D A|} = \frac{6}{18}

\frac{3}{3 + |D A|} = \frac{1}{3}

3 + |D A| = 9

|D A| = 6

Z podobieństwa trójkątów $S D C$ oraz $S A B$ mamy też

\frac{|S C|}{|S C| + |C B|} = \frac{|D C|}{|A B|}

\frac{5}{5 + |D A|} = \frac{6}{18}

\frac{5}{5 + |D A|} = \frac{1}{3}

5 + |D A| = 15

|D A| = 10

Ćwiczenie 23

Dany jest trójkąt prostokątny $A B C$ o kącie prostym przy wierzchołku $C$ . Punkt $D$ jest spodkiem wysokości poprowadzonej z wierzchołka $C$ tego trójkąta. Wykaż, że $|C D| = \sqrt{|A D| \cdot |B D|}$ .

RuQwSqpbn6pyL

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zacznij od udowodnienia, że trójkąty $A D C$ i $C B D$ są podobne. Korzystając z tego podobieństwa ułóż odpowiednią proporcję, która po przekształceniu utworzy poszukiwaną równość.

RZ2BLa5K1ZO1I1

Rysunek trójkąta A B C opisanego w zadaniu. Wysokość poprowadzona z wierzchołka C przecina się z podstawą AB tego trójkąta w punkcie D. Wysokość CD dzieli kąt prosty trójkąta na dwa kąty, kąt BCD o mierze alfa i kąt ACD o mierze dziewięćdziesiąt stopni minus alfa. Oznaczono również kąt CAD o mierze alfa i kąt CBD o mierze dziewięćdziesiąt stopni minus alfa. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Oznaczmy przez $α$ kąt w trójkącie $A B C$ znajdujący się przy wierzchołku $A$ . Zauważmy, ze trójkąty $A D C$ oraz $C B D$ mają kąty $90 °$ , $α$ , $90 ° - α$ . Zatem trójkąty $A D C$ oraz $C B D$ są podobne, na mocy cechy podobieństwa kąt – kąt – kąt. Możemy napisać proporcję

\frac{|C D|}{|B D|} = \frac{|A D|}{|C D|}

z której otrzymujemy

{|C D|}^{2} = |A D| \cdot |B D|

Ponieważ $|C D| > 0$ , to

|C D| = \sqrt{|A D| \cdot |B D|}

Ćwiczenie 24

RDZ3OBQt7aFYJ

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R9U8NZgqm0IoS1

Rysunek trapezu A B C D z przekątnymi AC i BD pomocniczy do rozwiązania zadania. Odcinek DS =3x, odcinek SB =5x. W trapezie zaznaczono pary kątów o tych samych miarach: BAC i ACD, ASB i CSD oraz CDS i ABS. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Kąty $A S B$ oraz $C S D$ są wierzchołkowe, zatem mają taką samą miarę. Kąty $D C S$ oraz $B A S$ są naprzemianległe. Ponieważ podstawy trapezu są równoległe, miary kątów $D C S$ i $B A S$ są równe. Podobnie równe są miary kątów naprzemianległych $S D C$ i $S B A$ .
Trójkąt $A S B$ jest podobny do trójkąta $C S D$ na mocy cechy kąt – kąt – kąt podobieństwa trójkątów. Skala podobieństwa wynosi $\frac{5}{3}$ .
Stąd

\frac{|A B|}{|C D|} = \frac{5}{3}

\frac{10}{|C D|} = \frac{5}{3}

Zatem

|C D| = 6

Ćwiczenie 25

W trójkącie $A B C$ podstawa $A B$ ma długość $24$ , a wysokość opuszczona na tę podstawę jest równa $9$ . W trójkąt ten wpisano prostokąt $D E F G$ , taki jak na rysunku. Boki tego prostokąta pozostają w stosunku $3 : 4$ , przy czym dłuższy bok leży na podstawie trójkąta $A B C$ . Oblicz pole wpisanego prostokąta.

R1IIbyB0aAloH1

Rysunek trójkąta A B C, opisanego w zadaniu, z wpisanym prostokątem D E F G. Punkty G i F zaznaczono odpowiednio na bokach AC i BC. Bok DE prostokąta leży na boku AB trójkąta. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RW2KkxwwbzuRG

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Odcinek $G F$ jest równoległy do $A B$ , skąd miary odpowiednich kątów są równe jako kątów odpowiadających. Trójkąt $C G F$ jest podobny do trójkąta $C A B$ na mocy cechy podobieństwa kąt – kąt – kąt.

RNfAADHeIsHDy1

Stosunek odpowiednich wysokości w trójkątach podobnych jest równy skali podobieństwa, czyli jest równy stosunkowi długości odpowiednich boków. Stąd otrzymujemy

\frac{9 - 3 x}{9} = \frac{4 x}{24}

\frac{3 - x}{3} = \frac{x}{6}

3 - x = \frac{x}{2}

6 = 3 x

x = 2

Boki prostokąta $E F G D$ są równe $3 x = 6$ oraz $4 x = 8$ , zatem pole jest równe $6 \cdot 8 = 48$ .

Ćwiczenie 26

Na zewnątrz trójkąta prostokątnego $A B C$ , w którym kąt $A C B$ jest prosty oraz $|A C| = 5$ i $|B C| = 12$ , zbudowano kwadrat $A C D E$ . Punkt $H$ należy do prostej $A B$ i $|∢ H E A| = 90 °$ . Oblicz pole trójkąta $H A E$ .

R1UO68MCvKxDw1

Rysunek trójkąta A B C i kwadratu A C D E zbudowanego na zewnątrz trójkąta. Krótsza przyprostokątna AC trójkąta jest jednocześnie bokiem kwadratu z zadania. Przedłużenie boku BA trójkąta i przedłużenie boku DE kwadratu przecina się w punkcie H. Powstał nam w ten sposób trójkąt BDH zbudowany z trzech figur: trójkąta prostokątnego ABC, kwadratu ACDE i trójkąta prostokątnego AEH. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1awityhI0ZHR

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Oznaczmy miarę kąta $A B C$ przez $α$ . Mamy wówczas

|∢ B A C| = 90 ° - α

Kąt $H A B$ jest kątem półpełnym, więc

|∢ H A E| = 180 ° - 90 ° - (90 ° - α) = α

Zatem trójkąty prostokątne $A B C$ i $H A E$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów. Z proporcji

\frac{5}{|E H|} = \frac{12}{5}

mamy

|E H| = \frac{25}{12}

Pole trójkąta $H A E$ wynosi

P_{H A E} = \frac{1}{2} \cdot |E H| \cdot |E A| = \frac{1}{2} \cdot \frac{25}{12} \cdot 5 = \frac{125}{24}

Ćwiczenie 27

R1TXK4Gy4dQHG

Dany jest równoległobok

A B C D

. Na przedłużeniu przekątnej

A C

poza punkt

C

, wybrano punkt

P

, taki że

|A C| = 3 |C P|

. Znajdź stosunek pola trójkąta

D C P

do pola równoległoboku

A B C D

. Uzupełnij odpowiedź, przeciągając w lukę odpowiednią liczbę lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.
Odpowiedź: Stosunek pola trójkąta

D C P

do pola równoległoboku

A B C D

wynosi 1.

\frac{1}{4}

, 2.

\frac{1}{6}

, 3.

\frac{1}{5}

, 4.

\frac{1}{7}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RGABJnH6G8dWQ1

Rysunek równoległoboku A B C D, o wysokości h, pomocniczy do rozwiązania zadania. Przekątna równoległoboku AC ma długość 3x. Odcinek CP leżący na przedłużeniu przekątnej AC ma długość x. Wysokość trójkąta D C P to h z indeksem dolnym jeden. Na przedłużeniu podstawy DC zaznaczono punkt E. Powstał w ten sposób trójkąt CEP. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zaznaczmy odcinek $P E$ równoległy do $B C$ oraz odcinek $C E$ równoległy do $A B$ . Powstały trójkąt $C E P$ jest podobny do trójkąta $A B C$ . Skala tego podobieństwa jest równa

k = \frac{x}{3 x} = \frac{1}{3}

Stosunek wysokości trójkątów podobnych jest równy skali podobieństwa $\frac{h_{1}}{h} = \frac{1}{3}$ , skąd $h = 3 h_{1}$ .
Trójkąt $D C P$ oraz równoległobok $A B C D$ mają podstawę tej samej długości. Oznaczmy ją przez $a$ .
Pola tych figur wyrażają się wzorami

P_{D C P} = \frac{1}{2} a h_{1}

P_{A B C D} = a h = a \cdot 3 h_{1}

Zatem stosunek tych pól jest równy

\frac{P_{D C P}}{P_{A B C D}} = \frac{\frac{1}{2} a h_{1}}{a \cdot 3 h_{1}} = \frac{1}{6}

Ćwiczenie 28

R1Bz5HtZp6kgt

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

ROWic90W9GvnD1

Rysunek trójkąta A B C służący pomocniczo do rozwiązania zadania. W trójkącie poprowadzono środkową CD, na której zaznaczono punkt K. Na boku AC zaznaczono punkt M. Prosta poprowadzona przez punkty M i L jest równoległa do boku BC trójkąta. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Długość odcinka $|D K|$ wynosi

|D K| = |C D| - |C K|

czyli

|D K| = 8 - 2 = 6

Oznaczmy przez $L$ punkt wspólny prostej $M K$ i boku $A B$ . Trójkąty $D K L$ i $D C B$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów (ponieważ proste $K L$ i $C B$ są równoległe, więc kąty odpowiadające są sobie równe). Otrzymujemy proporcję $\frac{|D B|}{|D L|} = \frac{|D C|}{|D K|}$ , czyli $\frac{|D B|}{|D L|} = \frac{8}{6} = \frac{4}{3}$ .
Oznaczmy długość odcinka $B L$ przez $x$ . Mamy wtedy $|D L| = 3 x$ oraz $|D B| = 4 x$ .
Punkt $D$ jest środkiem odcinka $A B$ . Stąd

|A D| = |D B| = 4 x

Trójkąt $A L M$ jest podobny do trójkąta $A B C$ (na mocy cechy kąt – kąt – kąt podobieństwa trójkątów). Mamy więc $\frac{|A M|}{|A C|} = \frac{|A L|}{|A B|}$ , czyli $\frac{|A M|}{|A C|} = \frac{7 x}{8 x} = \frac{7}{8}$ . Otrzymujemy

|A M| = \frac{7}{8} |A C|

skąd

|M C| = |A C| - |A M| = \frac{1}{8} |A C|

Szukany stosunek wynosi $\frac{|A M|}{|M C|} = \frac{\frac{7}{8} |A C|}{\frac{1}{8} |A C|} = 7$ . Ostatecznie $|A M| : |M C| = 7 : 1$ .

Ćwiczenie 29

RUz68tyayXwkd

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1Hf3uDrgBbdr1

Rysunek rombu A B C D opisanego w zadaniu. Z wierzchołka D poprowadzono wysokość DE prostopadłą do podstawy AB rombu. Poprowadzono przekątną AC, która przecina wysokość DE w punkcie F. Odcinek DF ma długość 13, a odcinek FE ma długość 12. Zaznaczono pary kątów o tej samej mierze: EAF i DCF, AEF i CDF oraz AFE i CFD. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Odcinek $D E$ jest wysokością rombu.
Trójkąty $A E F$ i $C D F$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów (odpowiednie kąty w obu trójkątach są równe jako wierzchołkowe albo naprzemianległe). Otrzymujemy proporcję $\frac{|A E|}{|C D|} = \frac{|E F|}{|D F|}$ , czyli $\frac{|A E|}{|C D|} = \frac{12}{13}$ . Oznaczmy

|A E| = 12 x

|C D| = 13 x

Czworokąt $A B C D$ jest rombem, stąd wszystkie jego boki mają tę samą długość, zatem $|A D| = |C D| = 13 x$ .
Z twierdzenia Pitagorasa dla trójkąta $A E D$ otrzymujemy

{(12 x)}^{2} + 25^{2} = {(13 x)}^{2}

{144 x}^{2} + 625 = {169 x}^{2}

{25 x}^{2} = 625

Ponieważ $x > 0$ , to

x = 5

Stąd

|A B| = 13 \cdot 5 = 65

Otrzymujemy pole

P = |A B| \cdot |D E| = 65 \cdot 25 = 1625

Ćwiczenie 30

R1AjvR6C0wfs1

W trójkącie prostokątnym

A B C

przyprostokątne mają długości

|A C| = 13, 6

|B C| = 25, 5

. Punkt

D

leży na przeciwprostokątnej

A B

|A D| = 8, 5

. Na przyprostokątnej

A C

leży taki punkt

E

, że proste

D E

A C

są prostopadłe. Na przyprostokątnej

B C

leży taki punkt

F

, że proste

D F

B C

są prostopadłe. Oblicz pole czworokąta

D F C E

. Uzupełnij odpowiedź, wpisując w lukę odpowiednią liczbę.
Odpowiedź: Pole czworokąta

D F C E

wynosi Tu uzupełnij.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1UAbWk9W3cwW1

Rysunek trójkąta prostokątnego A B C opisanego w zadaniu. Bok AC tego trójkąta ma długość 13,6, a bok BC ma długość dwadzieścia pięć i pół. W trójkąt wpisany jest prostokąt CEDF, którego bok CE leży w całości na boku AC trójkąta, a bok CF leży w całości na boku BC trójkąta. Wierzchołek D prostokąta leży na boku AB trójkąta. Zaznaczono pary kątów o tych samych miarach: DAE i BDF, AED i BFD oraz ADE i DBF. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

sposób $I$

Pole trójkąta $A B C$ jest równe

P_{A B C} = \frac{1}{2} \cdot 13, 6 \cdot 25, 5 = 173, 4

Z twierdzenia Pitagorasa dla trójkąta $A B C$ mamy

|A B| = \sqrt{{(13, 6)}^{2} + {(25, 5)}^{2}} = 28, 9

Długość odcinka $D B$ jest równa

|D B| = |A B| - |A D| = 28, 9 - 8, 5 = 20, 4

Trójkąty $A D E$ i $A B C$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów. Skala tego podobieństwa jest równa

k = \frac{8, 5}{28, 9} = \frac{85}{289} = \frac{5}{17}

Stosunek pól tych trójkątów jest równy kwadratowi skali podobieństwa $\frac{P_{A D E}}{P_{A B C}} = {(\frac{5}{17})}^{2} = \frac{25}{289}$ . Otrzymujemy

P_{A D E} = \frac{25}{289} P_{A B C}

Trójkąty $D B F$ i $A B C$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów i skala tego podobieństwa jest równa

k_{1} = \frac{20, 4}{28, 9} = \frac{204}{289} = \frac{12}{17}

Wtedy stosunek pól tych trójkątów jest równy $\frac{P_{D B F}}{P_{A B C}} = {(\frac{12}{17})}^{2} = \frac{144}{289}$ , skąd $P_{D B F} = \frac{144}{289} P_{A B C}$ .
Pole prostokąta $D F C E$ wynosi

P_{D F C E} = P_{A B C} - P_{A D E} - P_{D B F} = P_{A B C} - \frac{25}{289} P_{A B C} - \frac{144}{289} P_{A B C} = \frac{120}{289} P_{A B C}

czyli

P_{D F C E} = \frac{120}{289} \cdot 173, 4 = 72

sposób $II$

Z twierdzenia Pitagorasa dla trójkąta $A B C$ mamy

|A B| = \sqrt{{(13, 6)}^{2} + {(25, 5)}^{2}} = 28, 9

Długość odcinka $D B$ jest równa

|D B| = |A B| - |A D| = 28, 9 - 8, 5 = 20, 4

Trójkąty $A D E$ i $A B C$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów. Otrzymujemy więc $\frac{|E D|}{25, 5} = \frac{8, 5}{28, 9}$ , skąd

|E D| = 7, 5

Trójkąty $A B F$ i $A B C$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów. Otrzymujemy więc $\frac{|F D|}{13, 6} = \frac{20, 4}{28, 9}$ , skąd

|F D| = 9, 6

Szukane pole jest więc równe

P_{D F C E} = 7, 5 \cdot 9, 6 = 72

Ćwiczenie 31

W równoległoboku $A B C D$ dane są długości boków $|A B| = 12$ i $|B C| = 16$ . Punkt $E$ leży na boku $A B$ i $|A E| = 8$ . Punkt $F$ leży na boku $B C$ i $|C F| = 4$ . Proste $D E$ i $D F$ przecinają przekątną $A C$ w punktach odpowiednio $K$ i $L$ . Wykaż, że $|A K| = 2 |L C|$ .

R1C9L1W7McXJz

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wykorzystaj fakt, że trójkąty $C D K$ i $A E K$ są podobne oraz trójkąty $A D L$ i $C F L$ są podobne. Korzystając z tych podobieństw układaj odpowiednie proporcje w taki sposób, aby doprowadziły one do uzyskania poszukiwanej równości.

RNnhBlHUL0xaT1

Rysunek równoległoboku A B C D opisanego w zadaniu. Poprowadzono wysokość DE prostopadłą do podstawy AB, wysokość DF prostopadłą do podstawy BC oraz przekątną AC. Wysokość DE przecina się z przekątną AC w punkcie K, a wysokość DF przecina się z przekątną AC w punkcie L. Długość odcinka AE to 8, długość odcinka EB to 4, długość odcinka BF to 12 i długość odcinka FC to cztery. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Długości odcinków $E B$ i $B F$ są odpowiednio równe $4$ i $12$ .
Trójkąty $A E K$ i $C D K$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów (równe kąty są zaznaczone kolorami na rysunku).

RDqacqTxvSw9t1

Rysunek równoległoboku A B C D - pomocniczy do rozwiązania zadania. W równoległoboku zaznaczono punkt K na przecięciu przekątnej AC i wysokości DE prostopadłej do podstawy AB, tak że powstały trójkąty prostokątne A E K i C D K. Zaznaczono pary kątów o równych miarach: EAK i DCK, AEK i CDK oraz AKE i CKD. Odcinek DC ma długość 12, a odcinek AE ma długość osiem. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Mamy więc proporcję $\frac{|A E|}{|C D|} = \frac{|A K|}{|C K|}$ , czyli $\frac{|A K|}{|C K|} = \frac{8}{12}$ .
Stąd $|A K| = \frac{2}{3} |C K|$ .
Wiemy, że $|A C| = |A K| + |K C|$ . Zatem $|A K| = \frac{2}{5} |A C|$ .
Trójkąty $C F L$ i $A D L$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów (równe kąty są zaznaczone kolorami na rysunku).

RF0PPlPY51bAo1

Rysunek równoległoboku A B C D - pomocniczy do rozwiązania zadania. W równoległoboku zaznaczono punkt L na przecięciu przekątnej AC i wysokości DF prostopadłej do podstawy BC, tak że powstały trójkąty prostokątne A D L i C L F. Zaznaczono pary kątów o równych miarach: DAL i FCL, ADL i CFL oraz ALD i CLF. Odcinek AD ma długość 16, a odcinek CF ma długość cztery. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Mamy więc $\frac{|C F|}{|A D|} = \frac{|L C|}{|A L|}$ , czyli $\frac{|L C|}{|A L|} = \frac{4}{16}$ .
Stąd $|L C| = \frac{1}{4} |A L|$ .
Wiemy, że $|A C| = |A L| + |L C|$ . Zatem

|L C| = \frac{1}{5} |A C|

Otrzymujemy więc

\frac{|A K|}{|L C|} = \frac{\frac{2}{5} |A C|}{\frac{1}{5} |A C|} = 2

Stąd

|A K| = 2 |L C|

Ćwiczenie 32

R1TIPtZTGqZMz

W trójkącie

A B C

kąt przy wierzchołku

A

ma miarę większą od kąta przy wierzchołku

B

. Punkt

K

jest środkiem boku

A B

. Prosta zawierająca wysokość tego trójkąta, poprowadzona z wierzchołka

C

, przecina bok

A B

w punkcie

D

, przy czym

|A D| : |D B| = 5 : 11

. Symetralna boku

A B

przecina bok

B C

w punkcie

L

i przedłużenie boku

A C

w punkcie

M

. Oblicz podane stosunki i połącz je w pary z poprawnymi wynikami.

|B L| : |L C|

Możliwe odpowiedzi: 1.

5 : 3

, 2.

8 : 3

, 3.

5 : 6

|A C| : |C M|

Możliwe odpowiedzi: 1.

5 : 3

, 2.

8 : 3

, 3.

5 : 6

|K L| : |L M|

Możliwe odpowiedzi: 1.

5 : 3

, 2.

8 : 3

, 3.

5 : 6

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RDg7iwvUVaC2r1

Rysunek trójkąta A B C opisanego w zadaniu. Na boku AB trójkąta zaznaczono punkty D i K. Odcinek AD =5x, odcinek DK =3x i odcinek KB =8x. Poprowadzono wysokość CD prostopadłą do podstawy AB trójkąta. Poprowadzono symetralną podstawy AB w punkcie K. Na przecięciu symetralnej i boku BC trójkąta zaznaczono punkt L. Punkt przecięcia symetralnej i przedłużenia boku AC trójkąta oznaczono punktem M. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Oznaczmy długość odcinka $A D$ przez $5 x$ , a długość odcinka $D B$ przez $11 x$ . Punkt $K$ dzieli odcinek $A B$ na połowy. Stąd $|K B| = 8 x$ oraz $|D K| = 3 x$ .

Trójkąt $B K L$ jest podobny do trójkąta $B D C$ na mocy cechy kąt – kąt – kąt podobieństwa trójkątów. Stąd $\frac{|B K|}{|B D|} = \frac{|B L|}{|B C|}$ , czyli $\frac{|B L|}{|B C|} = \frac{8 x}{11 x} = \frac{8}{11}$ . Otrzymaliśmy więc

|B L| = \frac{8}{11} |B C|

stąd

|L C| = \frac{3}{11} |B C|

Szukany stosunek jest równy $\frac{|B L|}{|L C|} = \frac{\frac{8}{11} |B C|}{\frac{3}{11} |B C|} = \frac{8}{3}$ .

Trójkąt $A D C$ jest podobny do trójkąta $A K M$ na mocy cechy kąt – kąt – kąt podobieństwa trójkątów. Stąd $\frac{|A D|}{|A K|} = \frac{|A C|}{|A M|}$ , czyli $\frac{|A C|}{|A M|} = \frac{5 x}{8 x} = \frac{5}{8}$ . Otrzymaliśmy więc

|A C| = \frac{5}{8} |A M|

stąd

|C M| = \frac{3}{8} |A M|

Szukany stosunek jest równy $\frac{|A C|}{|C M|} = \frac{\frac{5}{8} |A M|}{\frac{3}{8} |A M|} = \frac{5}{3}$ .

Z podobieństwa trójkątów $B K L$ i $B D C$ mamy $\frac{|K L|}{|C D|} = \frac{|B K|}{|B D|} = \frac{8}{11}$ .

Stąd

|K L| = \frac{8}{11} |C D| = \frac{40}{55} |C D|

Z podobieństwa trójkątów $A D C$ i $A K M$ mamy

\frac{|C D|}{|K M|} = \frac{|A D|}{|A K|} = \frac{5}{8}

Stąd

|K M| = \frac{8}{5} |C D| = \frac{88}{55} |C D|

Otrzymujemy $\frac{|K L|}{|K M|} = \frac{\frac{40}{55} |C D|}{\frac{88}{55} |C D|} = \frac{5}{11}$ . Zatem

|K L| = \frac{5}{11} |K M|

skąd

|L M| = \frac{6}{11} |K M|

Szukany stosunek jest równy $\frac{|K L|}{|L M|} = \frac{\frac{5}{11} |K M|}{\frac{6}{11} |K M|} = \frac{5}{6}$ .

Ćwiczenie 33

R24Rko0VSQAkN

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R19sB1Os3TXfU1

Rysunek trapezu A B C D opisanego w zadaniu. Przekątne trapezu przecinają się w punkcie S. Prosta równoległa do podstaw poprowadzona przez punkt S przecina bok AC w punkcie L i bok BD w punkcie K. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Trójkąty $A B S$ i $C D S$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów (kąty o równej mierze są zaznaczone na rysunku kolorami).

Ro0bCMeSYFUcs1

Rysunek trapezu A B C D - pomocniczy do rozwiązania zadania. Poprowadzono obie przekątne i w punkcie ich przecięcia zaznaczono punkt S. Powstały dwa trójkąty: CDS i ABS. W trapezie zaznaczono kąty parami równe D A B i A D C, D C B i C B A oraz C S D i A S B. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Mamy proporcję $\frac{|A S|}{|C S|} = \frac{|A B|}{|C D|}$ , czyli $\frac{|A S|}{|C S|} = \frac{20}{5}$ , skąd $|A S| = 4 |C S|$ .
Oznaczmy długość boku $C S$ przez $x$ . Mamy wtedy $|A S| = 4 x$ oraz $|A C| = 5 x$ .
Trapez $A B C D$ jest równoramienny, więc trójkąty $A B S$ i $C D S$ też są równoramienne, zatem

|D S| = x

|B S| = 4 x

oraz

|B D| = 5 x

Trójkąty $B K S$ i $B C D$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów.

RRdyHb2fDtMqO1

Rysunek równoległoboku A B C D - pomocniczy do rozwiązania zadania. Poprowadzono obie przekątne i w punkcie ich przecięcia zaznaczono punkt S. Na boku BD zaznaczono punkt K, tak że odcinek SK jest równoległy do obu podstaw trapezu. Zaznaczono kolorem zielonym trójkąt BDC. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Mamy więc $\frac{|K S|}{|C D|} = \frac{|B S|}{|B D|}$ , czyli $\frac{|K S|}{5} = \frac{4 x}{5 x}$ . Stąd $|K S| = 4$ .
Analogicznie trójkąty $D L S$ i $D A B$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów.

RaH7H0EP511U01

Mamy więc $\frac{|L S|}{|C D|} = \frac{|A S|}{|A C|}$ , czyli $\frac{|L S|}{5} = \frac{4 x}{5 x}$ . Stąd $|L S| = 4$ .
Otrzymujemy

|K L| = |L S| + |K S| = 4 + 4 = 8

Ćwiczenie 34

RQq3p8vt9Lzdk

W trójkącie

A B C

dane są długości boków

|A C| = 8

|B C| = 12

|A B| = 10

. Na bokach

A B

B C

C A

wybrano odpowiednio takie punkty

D

E

F

, że czworokąt

C F D E

jest rombem. Oblicz długość boku tego rombu oraz długości odcinków

D B

D A

. Uzupełnij odpowiedź, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.
Odpowiedź: Długość tego rombu wynosi 1.

2

, 2.

3

, 3.

\frac{24}{5}

, 4.

\frac{22}{6}

, 5.

6

, 6.

5

, 7.

4

, 8.

\frac{26}{3}

, 9.

7

, 10.

\frac{25}{4}

, odcinek

D B

2

, 2.

3

, 3.

\frac{24}{5}

, 4.

\frac{22}{6}

, 5.

6

, 6.

5

, 7.

4

, 8.

\frac{26}{3}

, 9.

7

, 10.

\frac{25}{4}

i odcinek

D A

2

, 2.

3

, 3.

\frac{24}{5}

, 4.

\frac{22}{6}

, 5.

6

, 6.

5

, 7.

4

, 8.

\frac{26}{3}

, 9.

7

, 10.

\frac{25}{4}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Oznaczmy długość boku rombu przez $x$ . Mamy wówczas $|A F| = 8 - x$ , $|B E| = 12 - x$ .

RbA5cEzUnttqL1

Rysunek trójkąta A B C opisanego w zadaniu. W trójkąt wpisano romb CEDF, którego bok CF w całości leży na boku AC trójkąta, bok CE w całości leży na boku BC trójkąta, a punkt D leży na boku AB trójkąta. Dodatkowo przerywaną linią poprowadzono odcinek CD. Wszystkie boki rombu mają długość x, odcinek AF ma długość 8‑x, a odcinek BE ma długość 12‑x. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Trójkąty $A D F$ i $D B E$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów. Stąd otrzymujemy $\frac{|A F|}{|D E|} = \frac{|F D|}{|E B|}$ , czyli $\frac{8 - x}{x} = \frac{x}{12 - x}$ . Zatem

(8 - x) (12 - x) = x^{2}

96 - 12 x - 8 x + x^{2} = x^{2}

20 x = 96

x = \frac{24}{5}

Zatem

|F D| = |D E| = \frac{24}{5}

|A F| = 8 - \frac{24}{5} = \frac{16}{5}

|B E| = 12 - \frac{24}{5} = \frac{36}{5}

Trójkąty $A D F$ i $A B C$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów. Stąd otrzymujemy $\frac{|A F|}{|A C|} = \frac{|A D|}{|A B|}$ , czyli $\frac{\frac{16}{5}}{8} = \frac{|A D|}{10}$ . Stąd $|A D| = 4$ oraz

|D B| = |A B| - |A D| = 10 - 4 = 6

Ćwiczenie 35

Na bokach $A B$ , $B C$ i $A C$ trójkąta $A B C$ leżą odpowiednio takie punkty $D$ , $E$ i $F$ , że prosta $D E$ jest równoległa do boku $A C$ i prosta $D F$ jest równoległa do boku $B C$ . Pole trójkąta $A D F$ jest równe $18$ , a pole trójkąta $B D E$ jest równe $50$ . Oblicz pole trójkąta $A B C$ .

RoAzu1MaaHIer

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wykorzystaj fakt, że trójkąty $A D F$ , $B D E$ i $A B C$ są trójkątami podobnymi. Pamiętaj, że stosunek pól trójkątów podobnych jest równy kwadratowi podobieństwa tych trójkątów.

R1TMs3z0vbKLi1

Rysunek trójkąta A B C opisanego w zadaniu. Na boku AC zaznaczono punkt F, na boku AB zaznaczono punkt D, a na boku CB zaznaczono punkt E. Odcinek FD jest równoległy do boku BC, a odcinek DE jest równoległy do boku AC. Odpowiednie kąty w trójkątach A D F i B D E mają takie same miary. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Trójkąty $A D F$ i $A B C$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów oraz trójkąty $D B E$ i $A B C$ są podobne na mocy cechy kąt – kąt – kąt podobieństwa trójkątów.
Stosunek pól trójkątów podobnych jest równy kwadratowi podobieństwa, więc
$\frac{P_{A D F}}{P_{A B C}} = {(\frac{|A D|}{|A B|})}^{2}$ oraz $\frac{P_{D B E}}{P_{A B C}} = {(\frac{|B D|}{|A B|})}^{2}$ .
Ponieważ $|A D| > 0$ , $|A B| > 0$ , $|D B| > 0$ , to
$\frac{|A D|}{|A B|} = \sqrt{\frac{18}{P_{A B C}}}$ oraz $\frac{|B D|}{|A B|} = \sqrt{\frac{50}{P_{A B C}}}$ .
Zatem $|A D| = \sqrt{\frac{18}{P_{A B C}}} \cdot |A B|$ oraz $|B D| = \sqrt{\frac{50}{P_{A B C}}} \cdot |A B|$ .
Ponieważ $|A D| + |B D| = |A B|$ , to otrzymujemy równanie

\sqrt{\frac{18}{P_{A B C}}} |A B| + \sqrt{\frac{50}{P_{A B C}}} |A B| = |A B|

\sqrt{\frac{18}{P_{A B C}}} + \sqrt{\frac{50}{P_{A B C}}} = 1

\frac{\sqrt{18}}{\sqrt{P_{A B C}}} + \frac{\sqrt{50}}{\sqrt{P_{A B C}}} = 1

\sqrt{18} + \sqrt{50} = \sqrt{P_{A B C}}

\sqrt{P_{A B C}} = 3 \sqrt{2} + 5 \sqrt{2}

\sqrt{P_{A B C}} = 8 \sqrt{2}

P_{A B C} = 128