Automat do dowodzenia twierdzeń

W szkolnej matematyce jest coraz mniej miejsca na „klasyczną” geometrię, w szczególności na zagadnienia związane chociażby z tzw. punktami szczególnymi trójkąta, np. punktami przecięcia się dwusiecznych kątów trójkąta, symetralnych jego boków, czy środkowych. Narzędziem, które jest niezwykle przydatne do badania istnienia takich punktów jest twierdzenie Cevy, które głosi, że jeżeli punkty $D$, $E$, $F$ należą odpowiednio do boków $AB$, $BC$, $AC$ trójkąta $ABC$, jak na rysunku, to proste $AE$, $BF$, $CD$ przecinają się w jednym punkcie wtedy i tylko wtedy, gdy

RioMmYEh6wkJU

Ilustracja przedstawia trójkąt A B C oraz jego trzy wysokości. Z wierzchołka A poprowadzono odcinek A E padający na odcinek B C, z wierzchołka B poprowadzono odcinek B F padający na odcinek A C, natomiast z wierzchołka C poprowadzono odcinek C D padający na odcinek A B. Wszystkie trzy wewnętrze odcinki przecinają się w jednym punkcie.

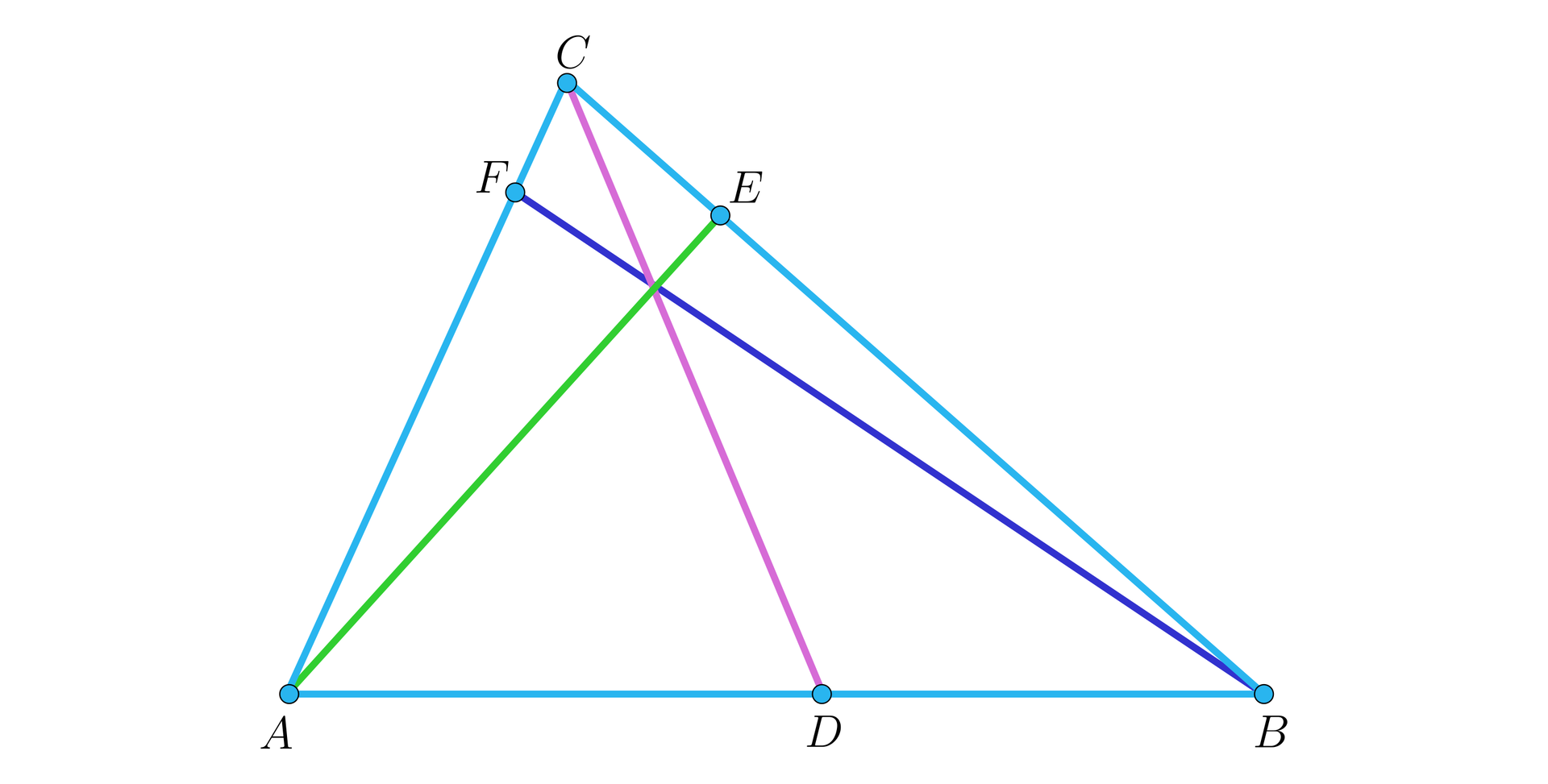
I choć istnienie ortocentrum wykażemy w inny sposób, to rozwiązując ćwiczenia, zaproponowane w poniższej lekcji, będziemy korzystać z tego użytecznego twierdzenia.