Przeczytaj
Jeśli nie będzie to zasygnalizowane inaczej, to punkty , , będą spodkami wysokości poprowadzonych odpowiednio na bok , oraz .
Przyjmijmy następującą definicję.
Punkt przecięcia się trzech prostych zawierających odpowiednio wysokości trójkąta będziemy nazywać ortocentrum tego trójkąta.
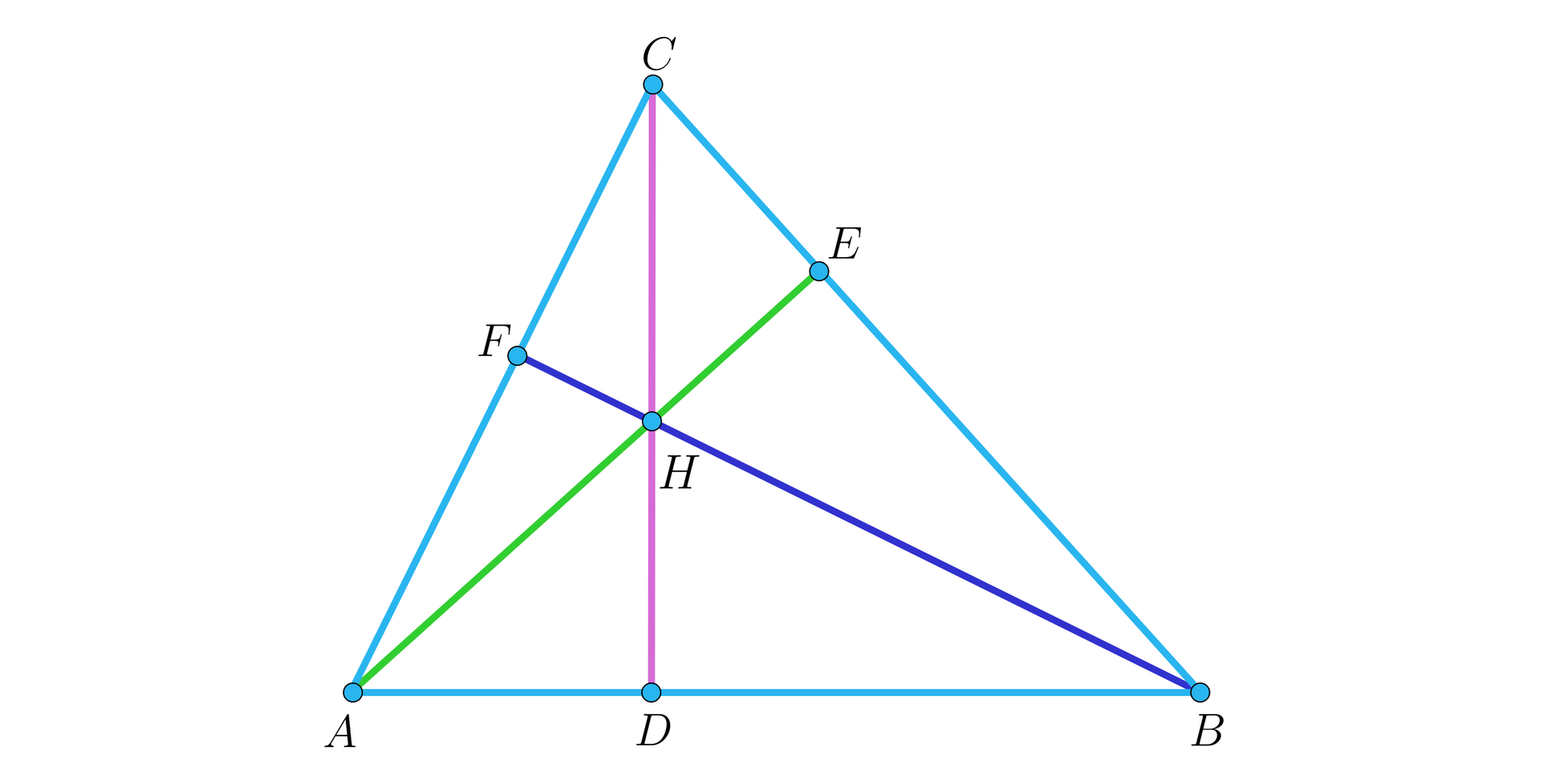
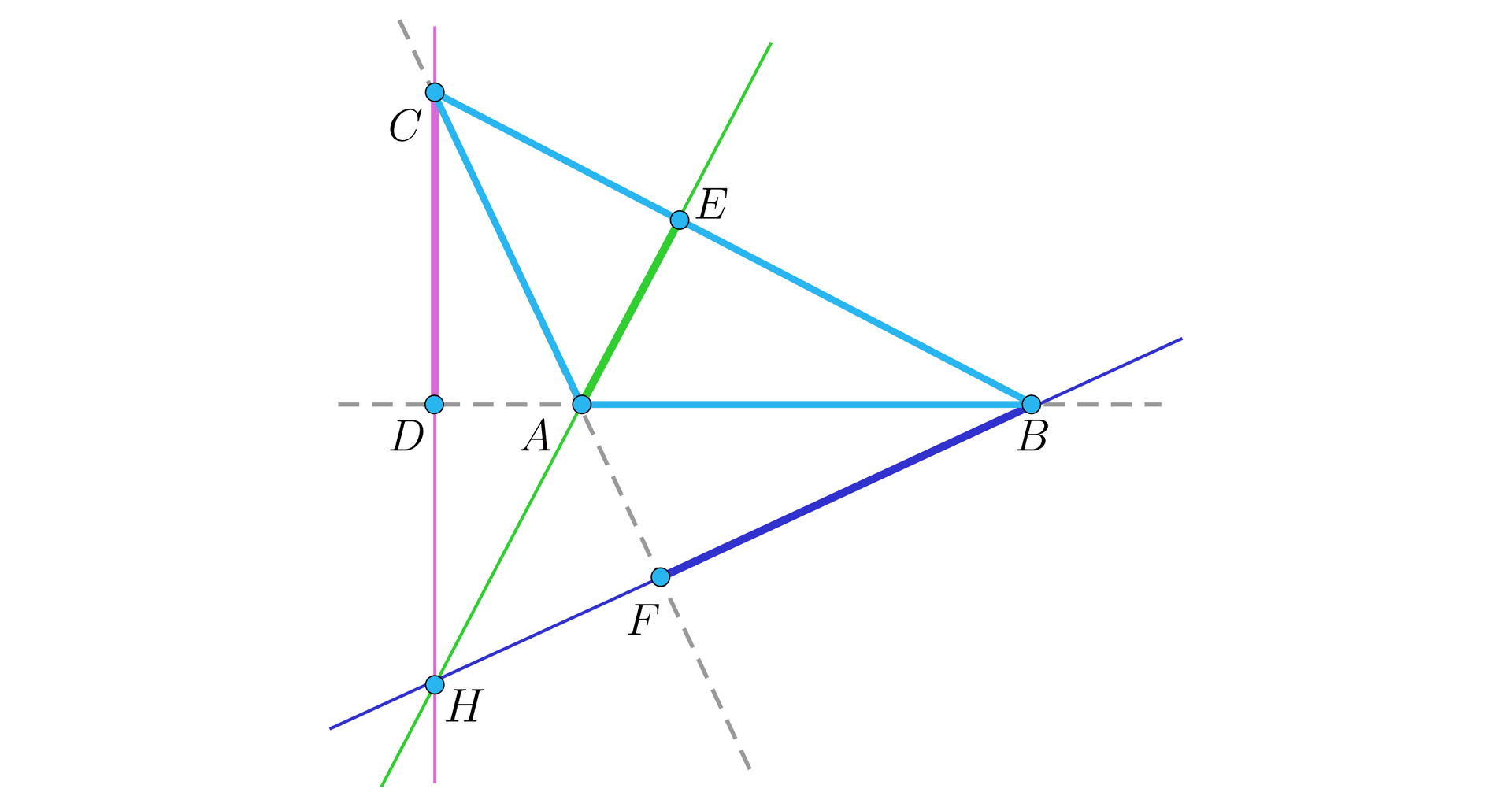
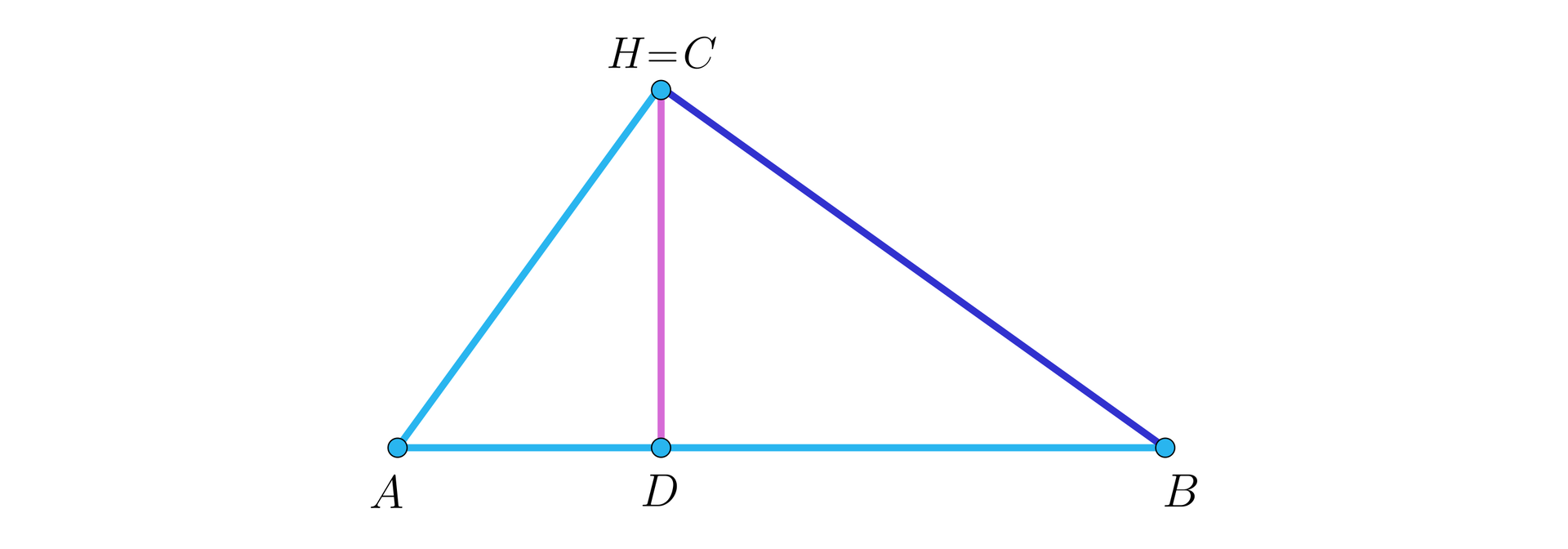
Zauważmy, że w trójkącie ostrokątnym czy prostokątnym ortocentrum jest punktem przecięcia się wysokości (odcinków), a w trójkącie rozwartokątnym jest punktem przecięcia się przedłużeń tych wysokości. Przyjęcie w definicji warunku przecinania się prostych jest ogólniejsze, co nie zmienia faktu, iż często o ortocentrum, także w przypadku trójkąta rozwartokątnego, mówi się, jako o punkcie przecinania się wysokości, a nie odpowiednich prostych i nie jest to traktowane jako błąd.
W definicji ortocentrum pojawia się warunek istnienia jednego punktu, w którym przetną się wszystkie trzy wysokości. Poniższe twierdzenie i jego dowód pokazują, że warunek ten jest spełniony dla dowolnego trójkąta.
Proste zawierające wysokości trójkątawysokości trójkąta przecinają się w jednym punkcie.
Rozważmy dowolny trójkąt i poprowadźmy przez każdy z jego wierzchołków prostą równoległą do przeciwległego boku, aż do przecięcia odpowiednio w punktach , , , jak na rysunku.
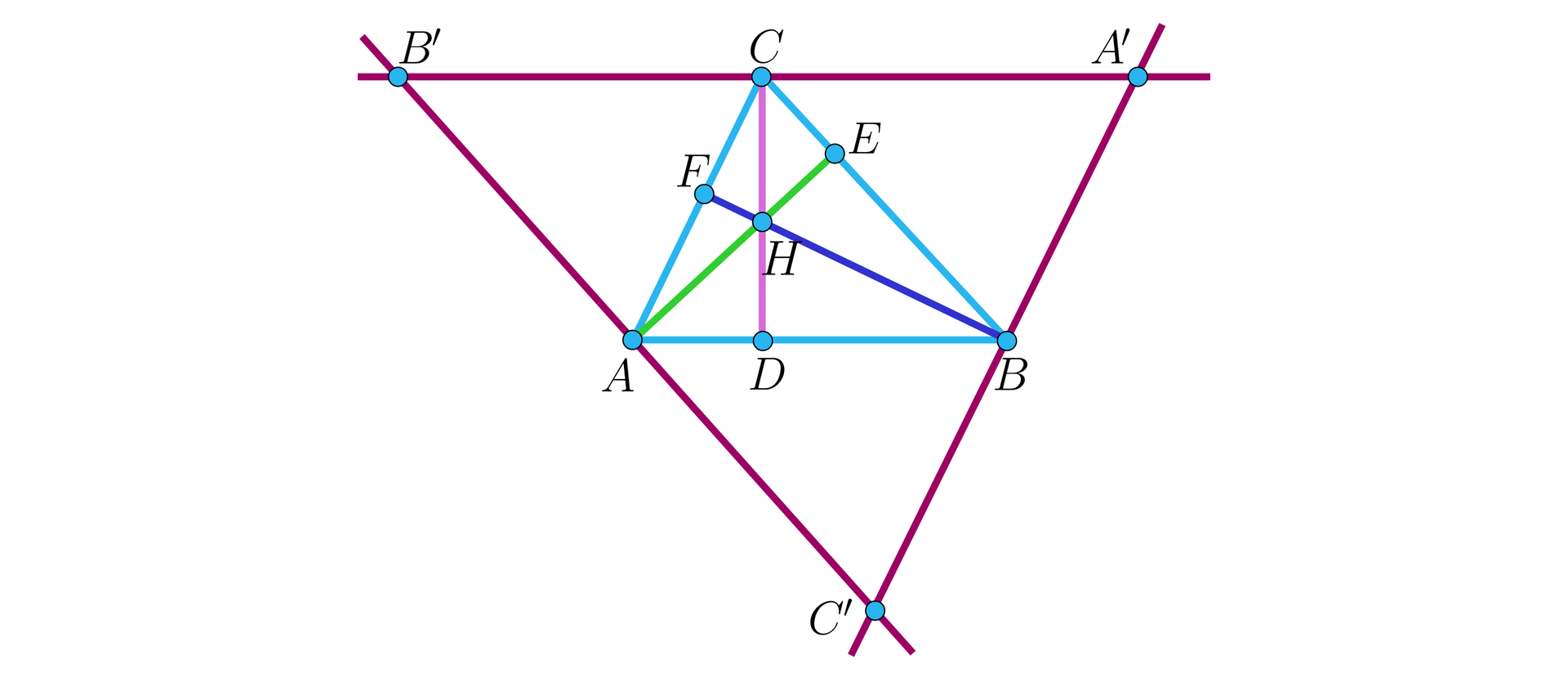
Zauważmy, że czworokąt jest równoległobokiem, a odcinek jest jego przekątną, stąd w szczególności trójkąty oraz są przystające.
Podobnie, korzystając z własności równoległoboków oraz stwierdzamy, że trójkąty oraz i oraz są także przystające.
Stąd wynika, że punkty , , są środkami odpowiednich boków trójkąta , a proste , oraz są symetralnymi odpowiednich boków trójkąta .
Korzystając ze znanej własności, że symetralne przecinają się w jednym punkcie otrzymujemy tezę twierdzenia.
Rzadziej przywoływaną własnością ortocentrum jest ta, o której mówi poniższe twierdzenie.
Niech punkt , różny od każdego z wierzchołków trójkąta , będzie jego ortocentrum. Wtedy każdy z wierzchołków , , jest ortocentrum w trójkącie, którego wierzchołkami są punkt i pozostałe wierzchołki tego trójkąta.
Zauważmy, że punkt będzie różny od każdego z wierzchołków trójkąta , tylko wtedy, gdy trójkąt ten nie będzie prostokątny.
Rozważmy trójkąt , jak na rysunku.
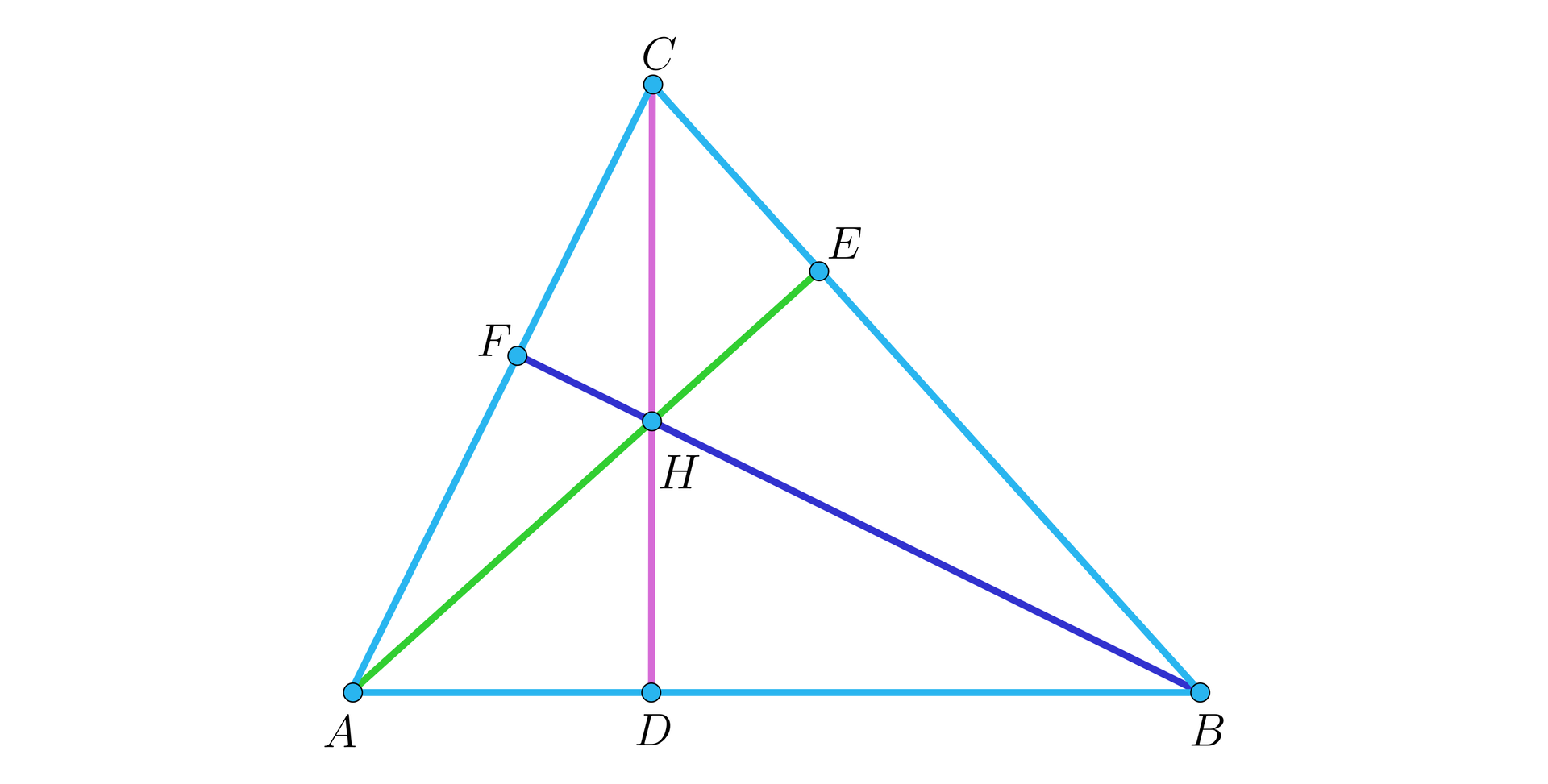
Zauważmy wówczas, że prosta zawiera wysokość , prosta zawiera wysokość , a prosta zawiera wysokość trójkąta . Co oznacza, że punkt jest ortocentrum trójkąta .
Problem Fagnana
Dany jest trójkąt , który nie jest prostokątny. Trójkąt , którego wierzchołkami są spodki wysokości danego trójkąta nazywamy trójkątem ortycznym albo spodkowym.
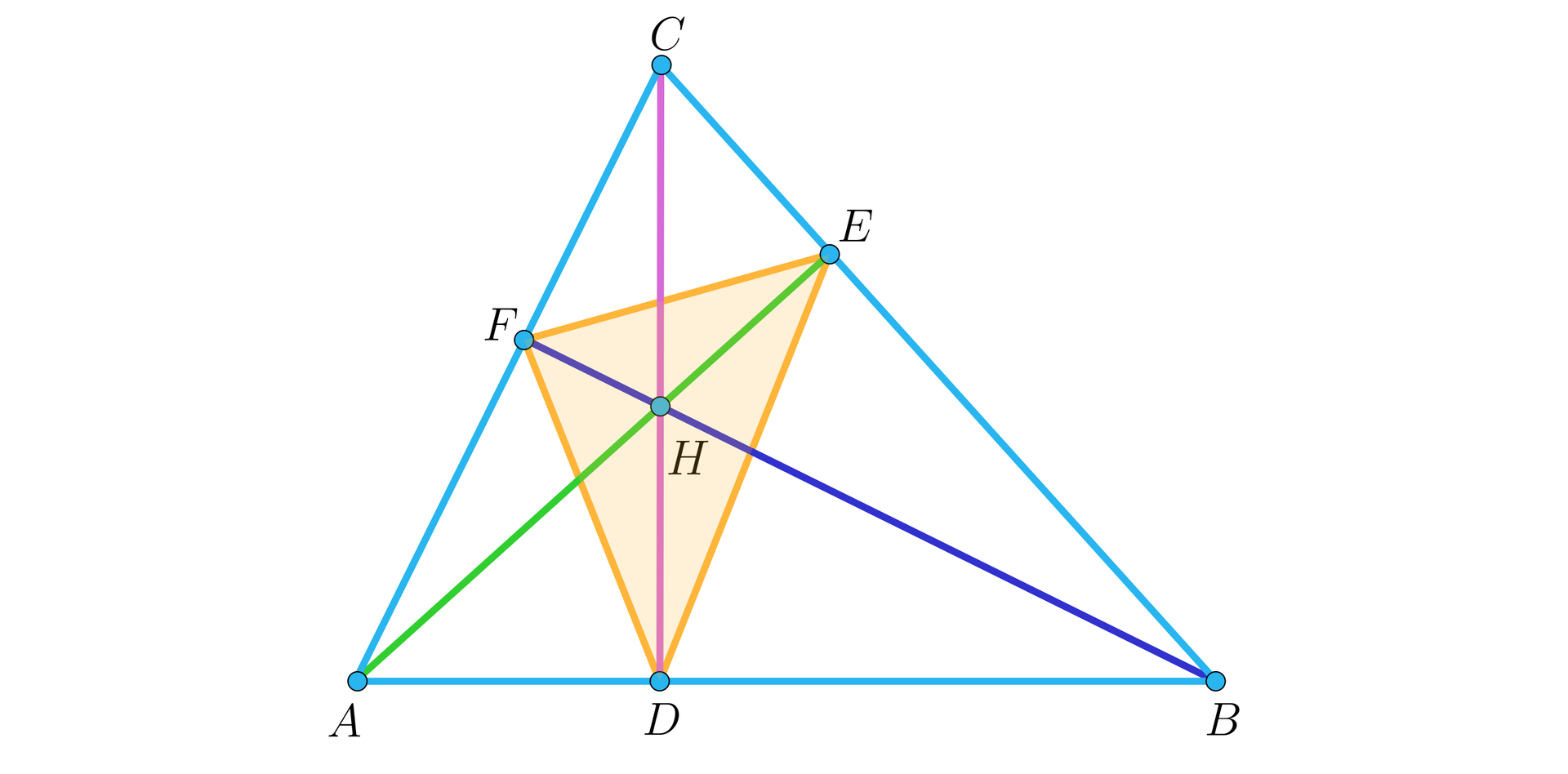
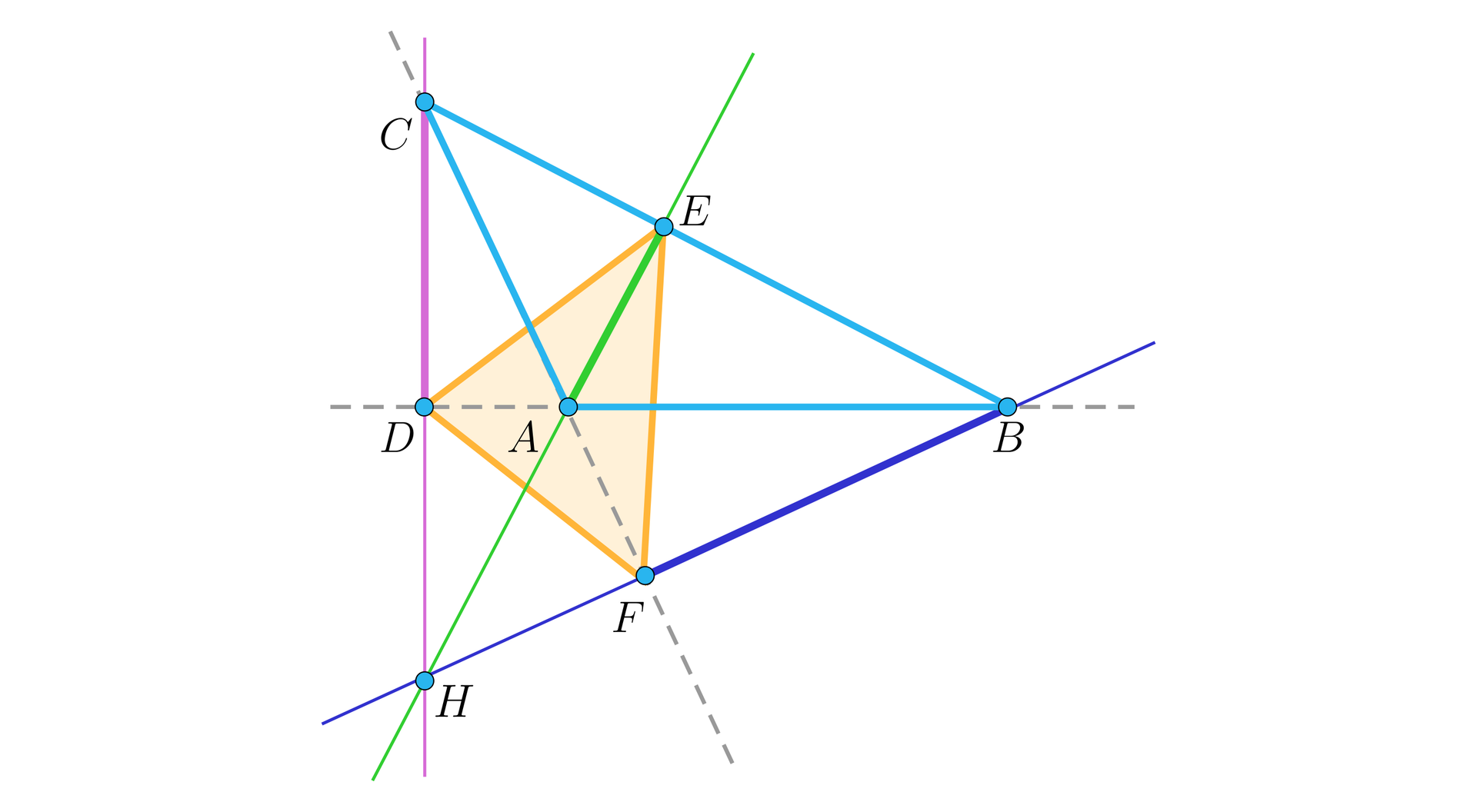
Problemem Fagnana nazywa się problem optymalizacyjny związany z wyznaczeniem trójkąta o najmniejszym obwodzie, którego każdy z wierzchołków leży na innym z trzech boków danego trójkąta ostrokątnego. Problem ten został postawiony przez włoskiego matematyka i duchownego Giovanniego Fagnana w roku. Okazuje się, że jego rozwiązaniem jest trójkąt ortycznytrójkąt ortyczny.
Rozważmy trójkąt równoramienny o podstawie długości i ramieniu . Wyznaczymy obwód trójkąta ortycznego oraz odległość ortocentrum trójkąta od jego podstawy.
Przyjmijmy oznaczenia jak na rysunku.
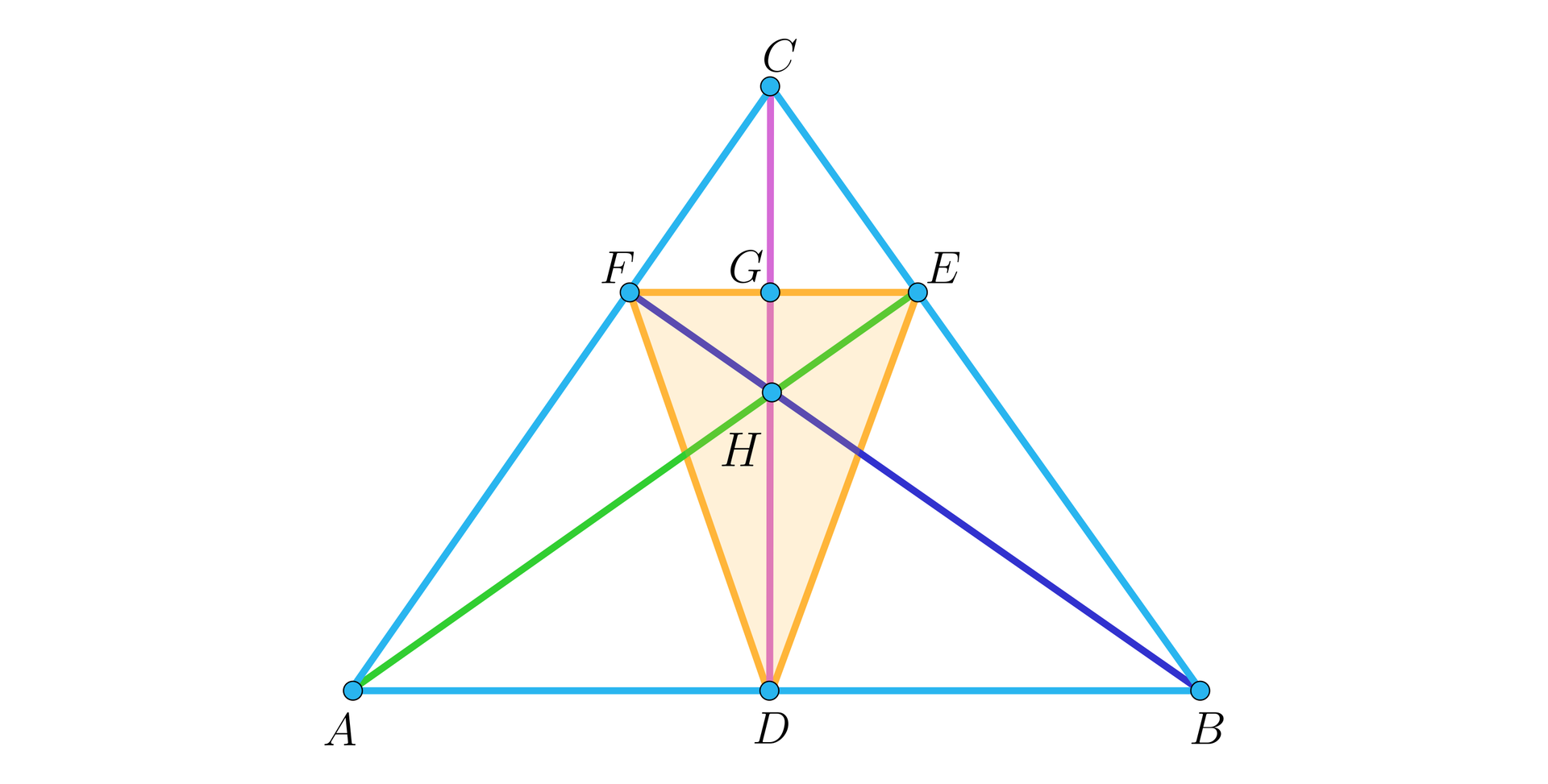
Wtedy , oraz .
Stąd .
Ponieważ , więc .
Ponadto oraz .
Stąd oraz .
Zatem .
Szukany obwód jest więc równy .
Ponieważ trójkąty i są podobne w skali oraz , więc .
Stąd .
Ortocentrum a okrąg opisany na trójkącie
Na koniec warto wspomnieć o ciekawej własności ortocentrum – jej dowód pominiemy, ale dociekliwy uczeń może podjąć samodzielną próbę uzasadnienia.
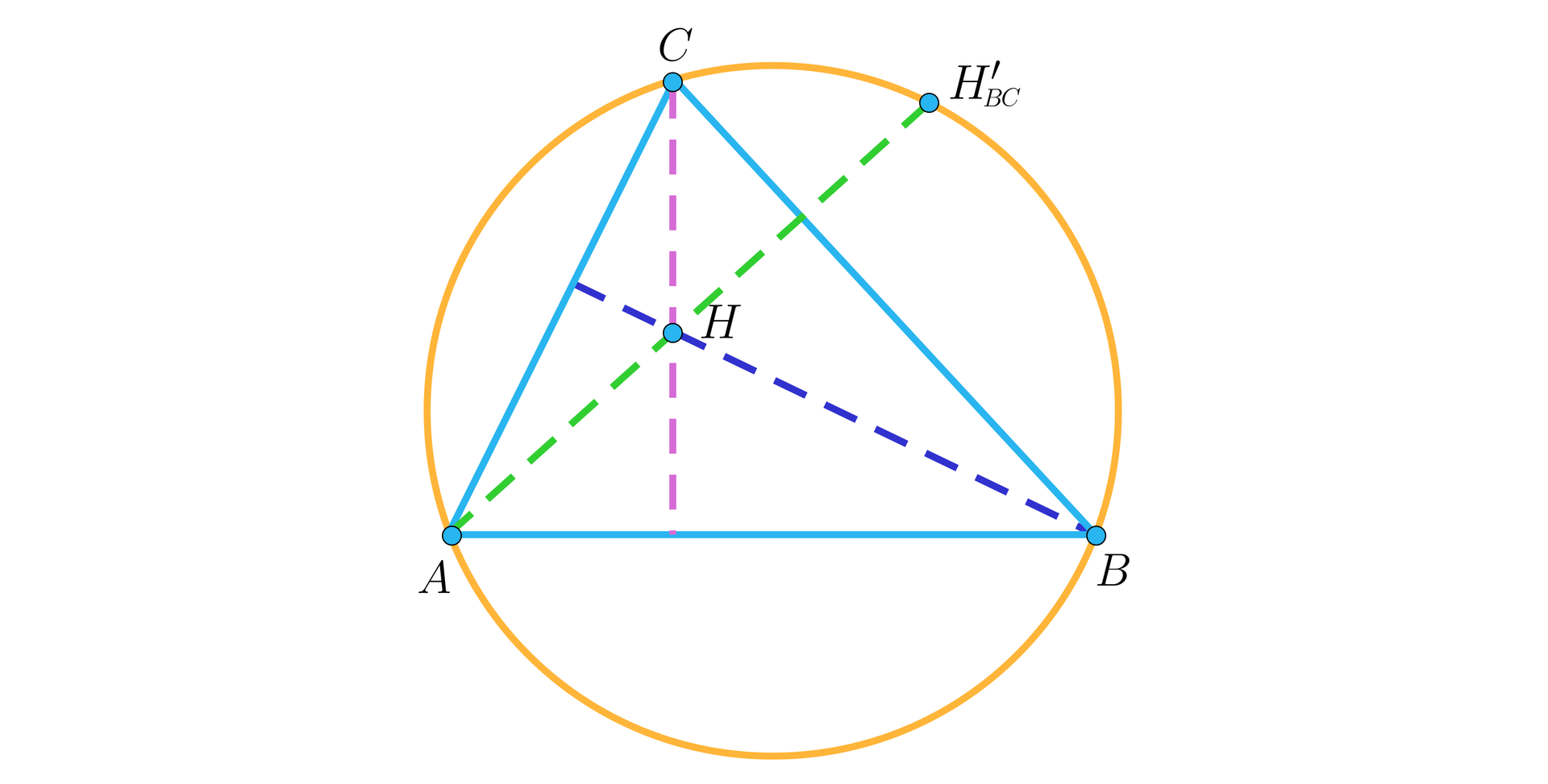
Obraz ortocentrum trójkąta w symetrii względem dowolnej prostej zawierającej bok tego trójkąta leży na okręgu opisanym na tym trójkącie.
Słownik
wysokością trójkąta jest najkrótszy z odcinków łączących wierzchołek trójkąta z prostą zawierającą przeciwległy bok
trójkąt, którego wierzchołkami są spodki wysokości danego trójkąta nazywamy jego trójkątem ortycznym