Wielokąty cykliczne

Powszechnie znany jest fakt, iż na każdym trójkącie można opisać okrąg i okrąg ten jest wyznaczony jednoznacznie. Inaczej sytuacja wygląda w przypadku wielokątów o większej niż $3$ liczbie boków. Zauważmy na poniższym rysunku, że okrąg opisany na czworokącie $ABCD$ jest tym samym okręgiem, który jest opisany na każdym z trójkątów, którego trzy wierzchołki są różnymi elementami zbioru $\left\{A, B, C, D\right\}$. Na poniższym rysunku zaznaczono trójkąty $ACD$ i $BCD$, które są wpisane w okrąg opisany na czworokącie $ABCD$.

R1a7yymdzpGs1

Ilustracja przedstawia czworokąt o wierzchołkach A B C D, w którym poprowadzono przekątne, kolorem niebieskim zaznaczono powstały trójkąt A C D, a kolorem różowym trójkąt B C D. Czworokąt jest wpisany w okrąg.

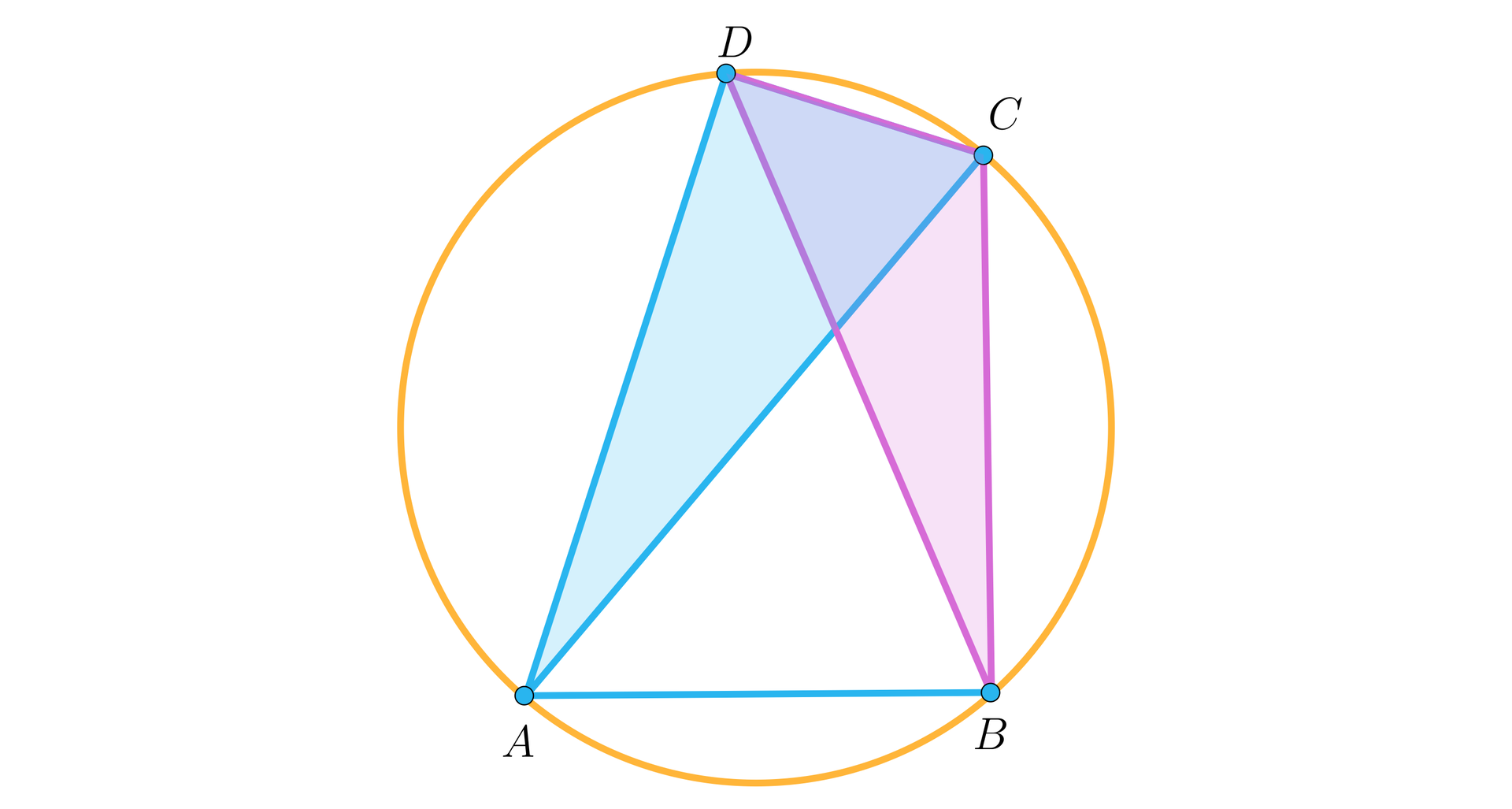
Dlatego też nie jest możliwe opisanie okręgu na rombie, który nie jest kwadratem, bo jak widać na poniższym rysunku, okręgi opisane na trójkątach $ACD$ i $ABC$ mają różne położenie na płaszczyźnie, choć oczywiście ich promienie są takie same.

R1JcCk1AnkPCH

Ilustracja przedstawia romb o wierzchołkach A B C D, w którym poprowadzono przekątną, kolorem niebieskim zaznaczono powstały trójkąt A C D, a kolorem różowym trójkąt A B C, trójkąty te są takie same. Przez punkty A B C poprowadzono jeden okrąg, a przez punkty A D C poprowadzono drugi okrąg. Okręgi przecinają się w punktach A oraz C. Przekątna rombu A C jest cięciwą okręgów.

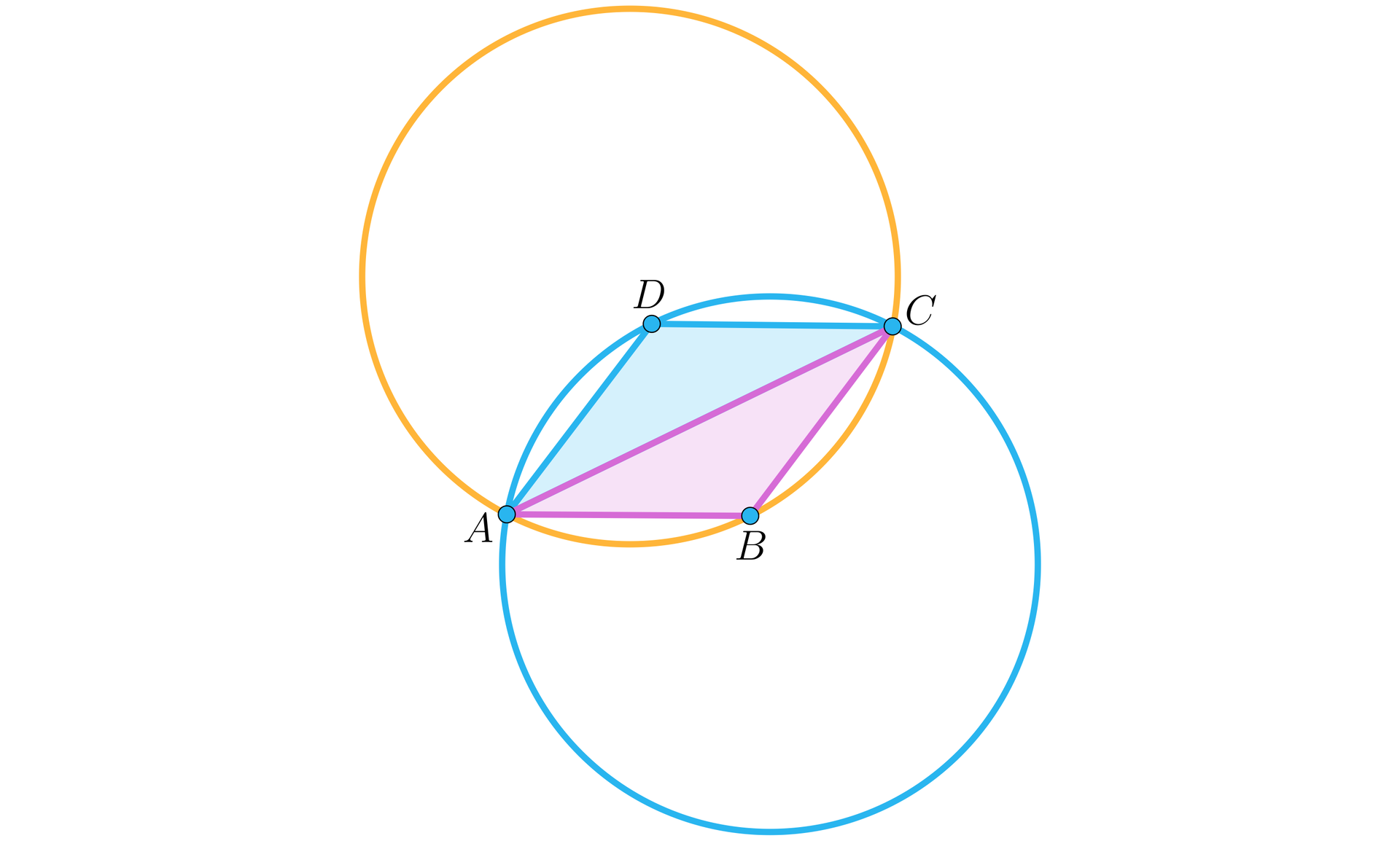
O wielokątach wypukłych, na których można opisać okrąg mówimy, że są one cykliczne. Niniejsza lekcja ma za zadanie podać warunek konieczny i wystarczający, by na czworokącie dało się opisać okrąg.