Przeczytaj
Będziemy mówić, że –kąt wypukły jest wielokątem cyklicznym, jeżeli da się na nim opisać okrąg.
Istnieje proste kryterium opisywalności okręgu na czworokącie, o czym mówi poniższe twierdzenie.
Czworokąt wypukły jest cykliczny wtedy i tylko wtedy, gdy suma miar przeciwległych kątów jest równa .
Najpierw zajmiemy się warunkiem koniecznym. Przypuśćmy zatem, że czworokąt jest wpisany w okrąg o środku . Poprowadźmy promienie i , jak na rysunku.
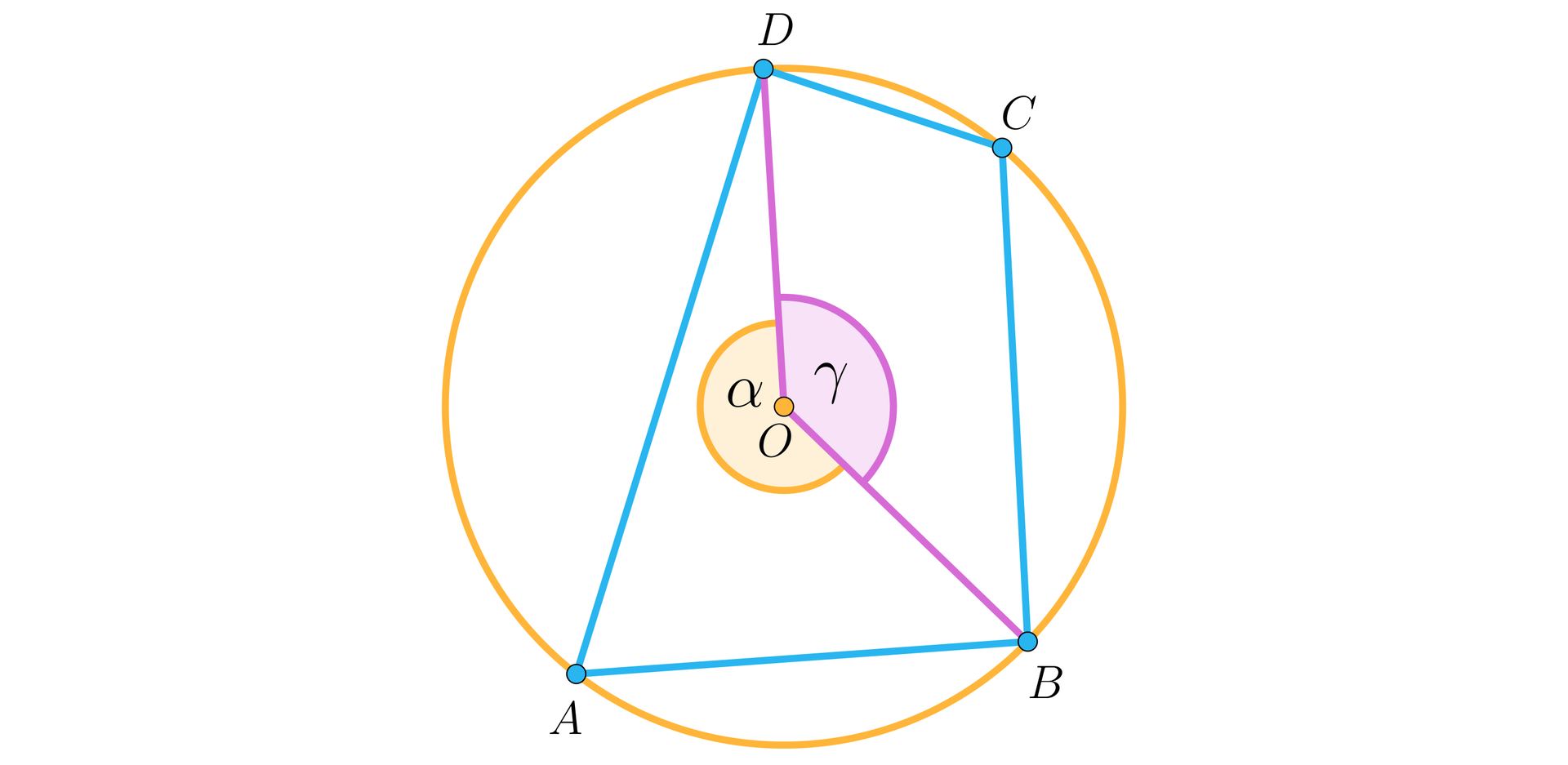
Pokażemy, że suma miar kątów i jest równa .
Zauważmy, że kąt jest kątem wpisanym opartym na tym spośród łuków o końcach , do którego należy punkt . Tym samym jego miara jest połową miary kąta środkowego opartego na tym samym łuku. Podobnie kąt jest kątem wpisanym opartym na tym spośród łuków o końcach , do którego należy punkt . Tym samym jego miara jest połową miary kąta środkowego opartego na tym samym łuku.
Ale , stąd .
Suma miar wszystkich kątów wewnętrznych czworokąta wypukłego jest równa , zatem również suma miar kątów i jest równa .
Teraz zajmiemy się warunkiem dostatecznym. Przypuśćmy zatem, że w czworokącie mamy i rozważmy okrąg o środku opisany na trójkącie . Rozważmy dowolny punkt leżący na łuku o końcach , w tej samej półpłaszczyźnie o krawędzi , co punkt , jak na rysunku.
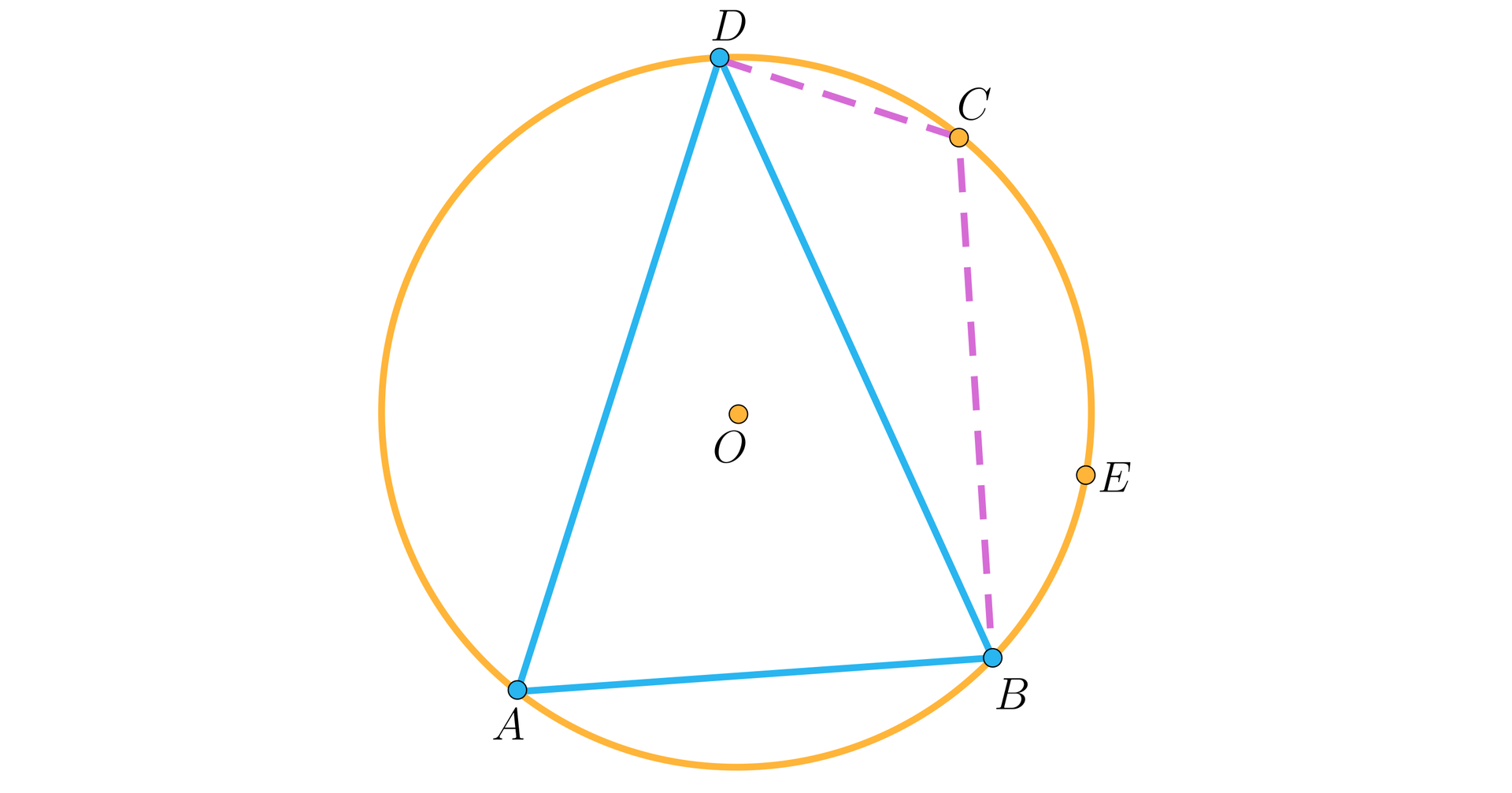
Z udowodnionego już warunku koniecznego wiemy, że .
Co oznacza, że .
Ale wiemy również, że miejscem geometrycznym punktów, z których odcinek widać pod tym samym kątem jest łuk okręgu (o czym była mowa w lekcji o zależnościach między kątami w kole). Tym samym punkt leży na łuku tego samego okręgu co punkt .
Zanim przejdziemy do rozwiązywania zadań związanych z czworokątami cyklicznymiczworokątami cyklicznymi, przywołamy klasyczną wersję twierdzenia Ptolemeusza. Przyjmiemy oznaczenia, jak na rysunku.
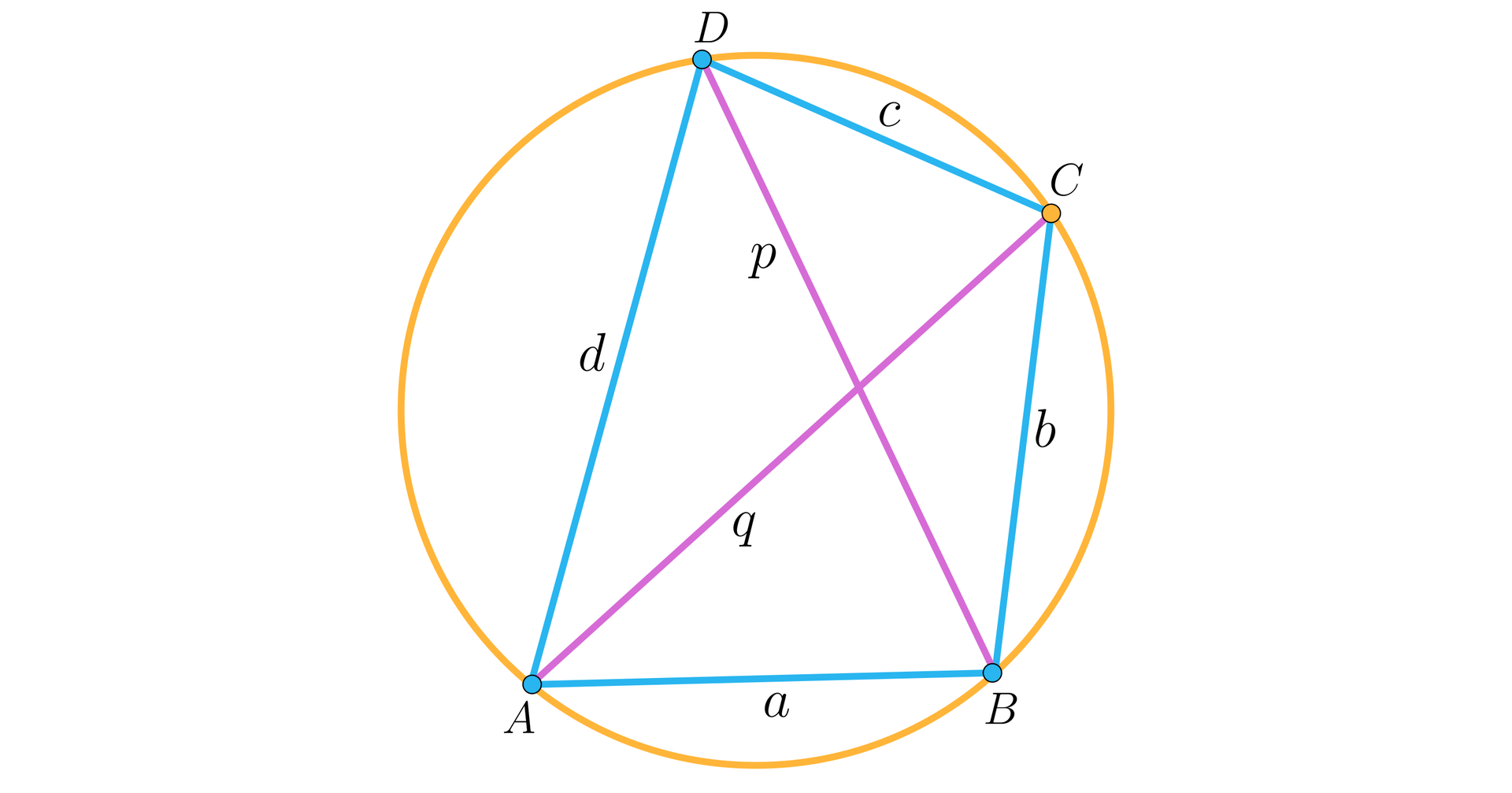
W dowolnym czworokącie wpisanym w okrąg iloczyn długości jego przekątnych jest równy sumie iloczynów długości przeciwległych boków.
Przy oznaczeniach z powyższego rysunku twierdzenie orzeka, że .
Rozważmy taki punkt leżący na przekątnej , że .
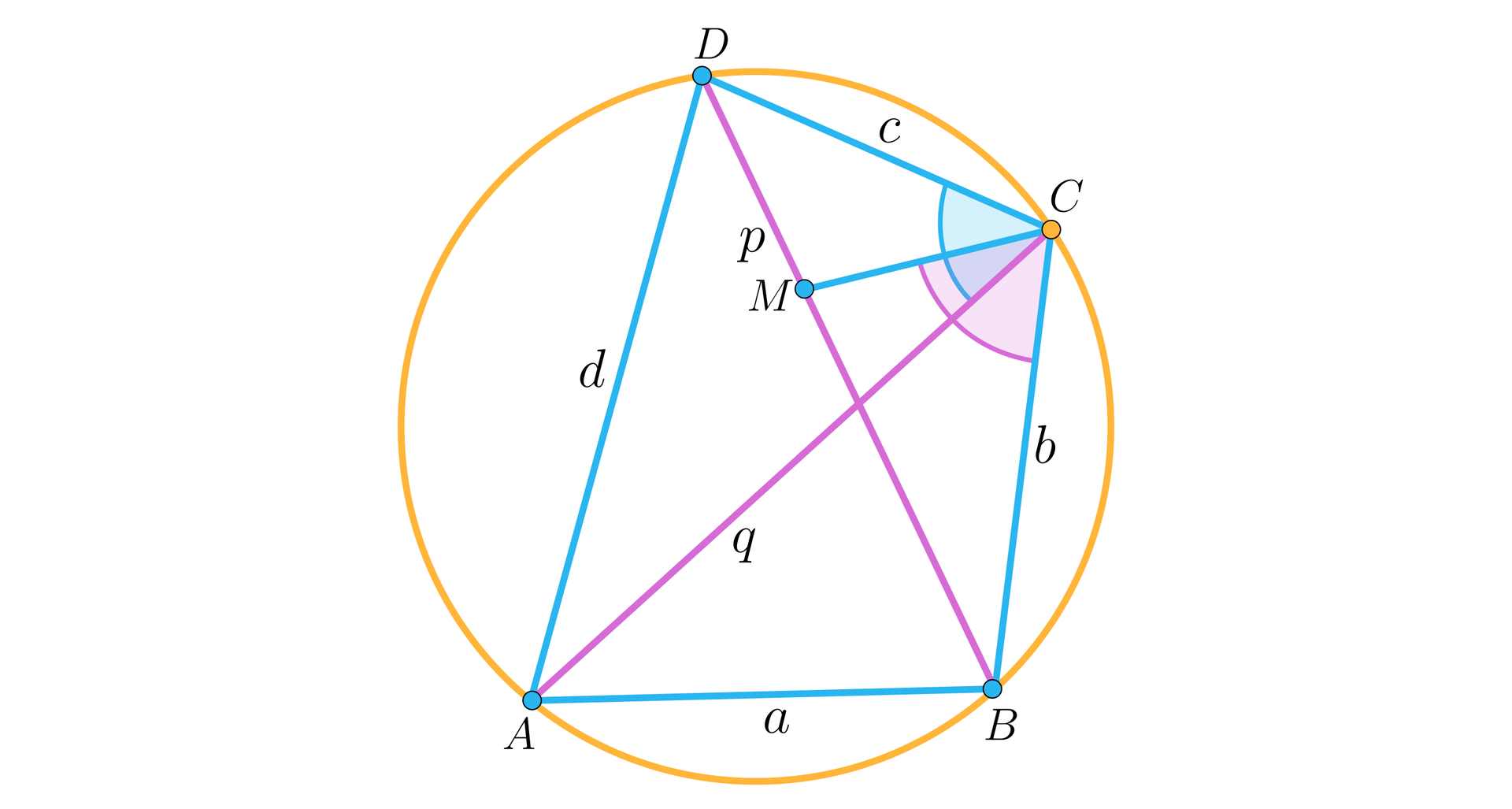
Zauważmy, że kąty i mają równe miary, jako kąty wpisane oparte na tym samym łuku.
Tym samym trójkąty i , na mocy cechy , są podobne.
W szczególności mamy więc, że . Stąd .
Analogicznie podobne są także trójkąty i . Stąd , czyli .
Otrzymujemy więc układ równań , który przy oznaczeniach z rysunku przyjmuje prostszą postać: .
Dodając stronami równania tego układu i wyłączając wspólny czynnik otrzymujemy: , co kończy dowód twierdzenia.
Pozostaje dodać, że prawdziwe jest również twierdzenie odwrotne, a w dowolnym czworokącie wypukłym zachodzi nierówność , zwana także nierównością Ptolemeuszanierównością Ptolemeusza.
Rozważmy czworokąt wpisany w okrąg w którym dane są: , , , . Wyznaczymy długości jego przekątnych.
Przyjmijmy oznaczenia, jak na rysunku.
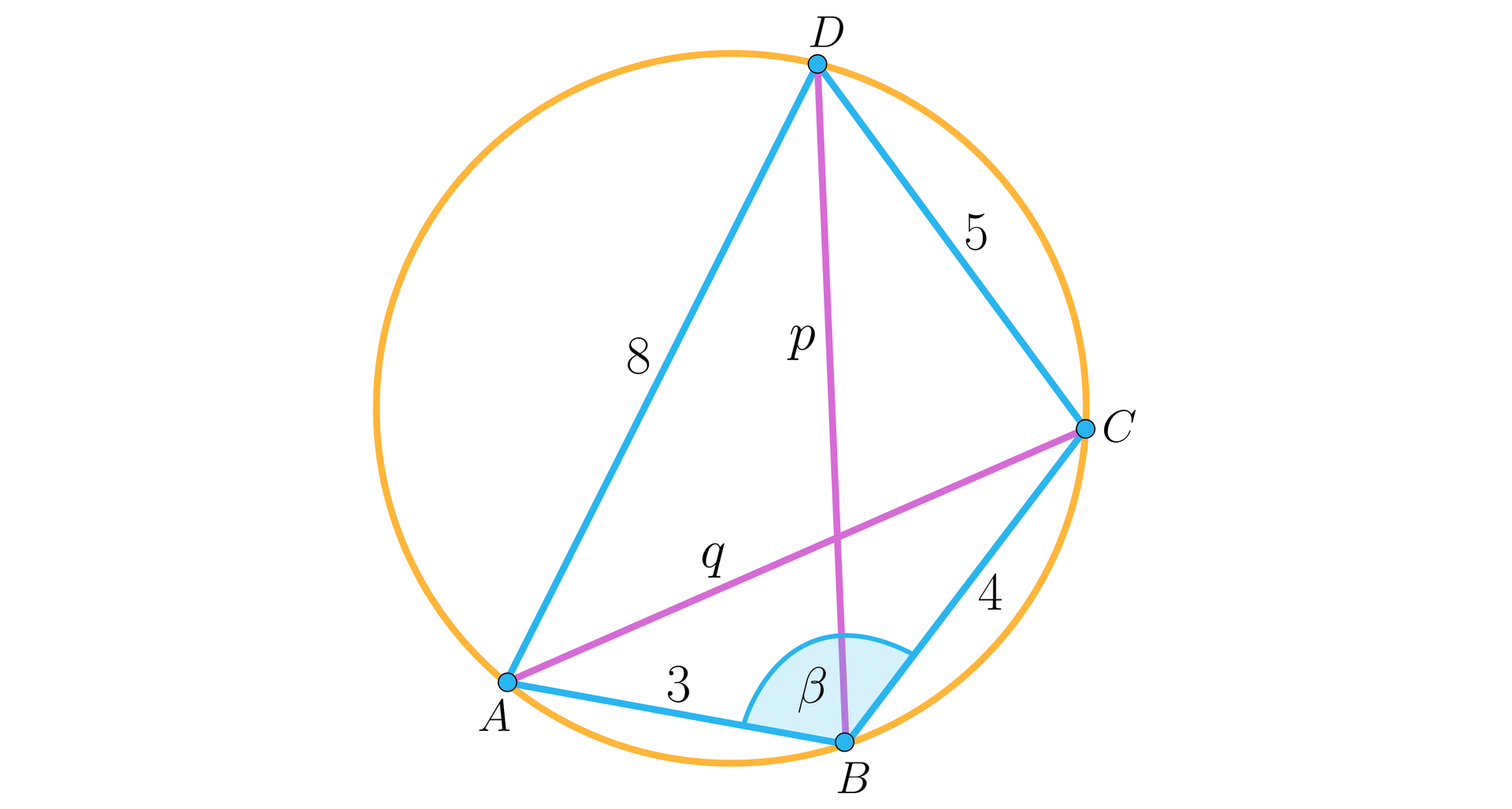
Ponieważ czworokąt jest cykliczny, to . Zatem .
Korzystając z twierdzenia cosinusów dla trójkątów i otrzymujemy:
,
.
Z pierwszego z równań otrzymujemy, że , zatem . Stąd .
Wyznaczając długość przekątnej możemy powtórzyć powyższy schemat.
Ale możemy też skorzystać z twierdzenia Ptolemeusza.
Otrzymujemy wtedy, że . Zatem .
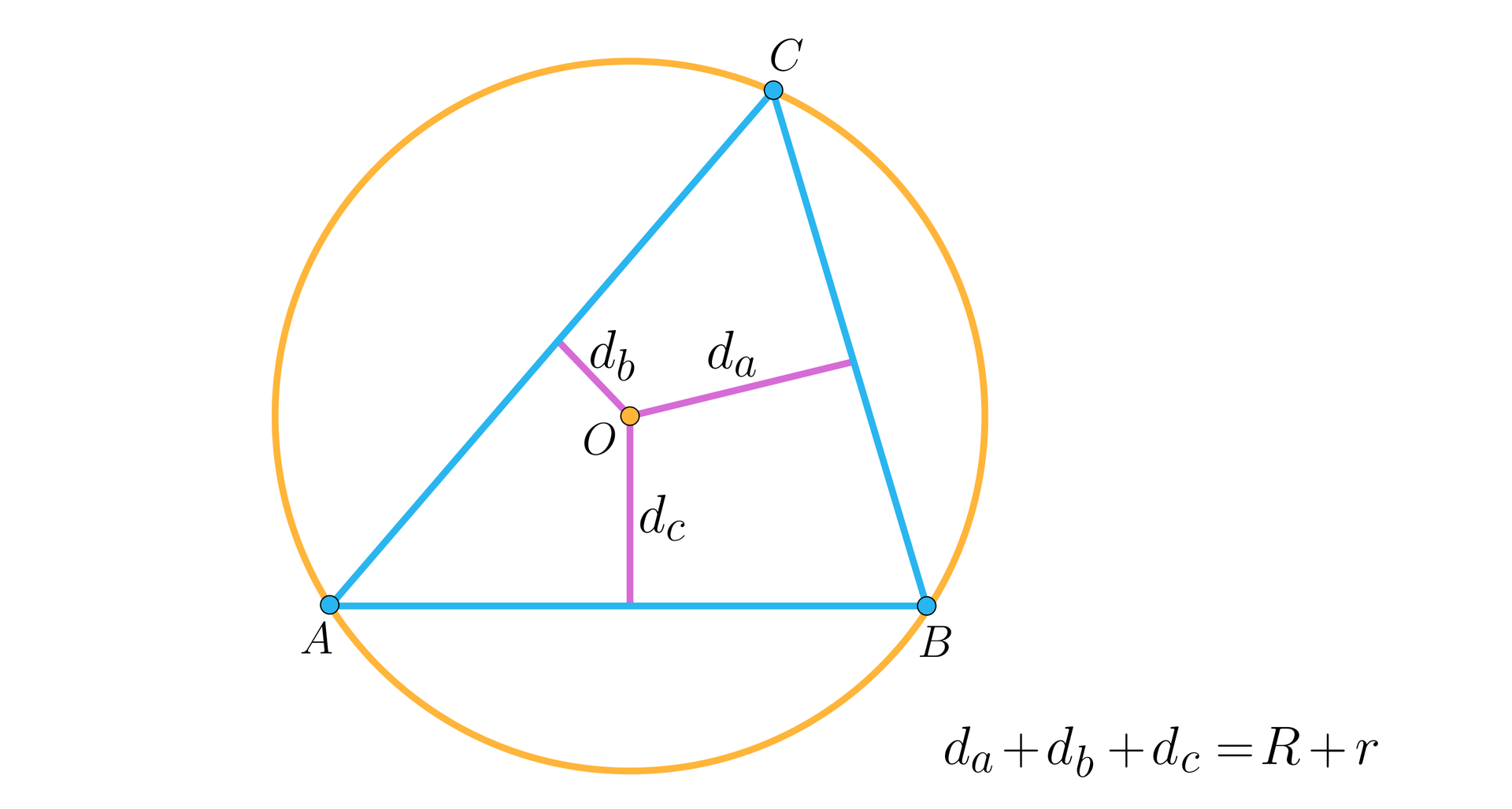
Na koniec przywołamy twierdzenie Carnot’a, które bezpośrednio nie dotyczy czworokątów, ale w którego dowodzie warto skorzystać z udowodnionego wcześniej twierdzenia Ptolemeusza. Jakkolwiek dowód tego twierdzenia tutaj pominiemy, to jego istotna część jest przedmiotem jednego z ćwiczeń dołączonych do lekcji.
Suma odległości środka okręgu opisanego na trójkącie od jego trzech boków jest równa sumie długości promieni okręgów opisanego i wpisanego w ten trójkąt.
Słownik
wielokątem cyklicznym nazywamy wielokąt wypukły, który da się wpisać w okrąg
w dowolnym czworokącie iloczyn długości jego przekątnych jest nie większy niż suma iloczynów długości przeciwległych boków (równość zachodzi tylko dla czworokąta cyklicznego)