Wprowadzenie - Zintegrowana Platforma Edukacyjna

Rb1qACOcoj3pI

Wiesz już, że pole trójkąta o dwóch bokach długości $a$ oraz $b$ i kącie ostrym $α$ pomiędzy tymi bokami jest równe:

$P = \frac{1}{2} a b \sin α$

Ru4OxygyVuroj1

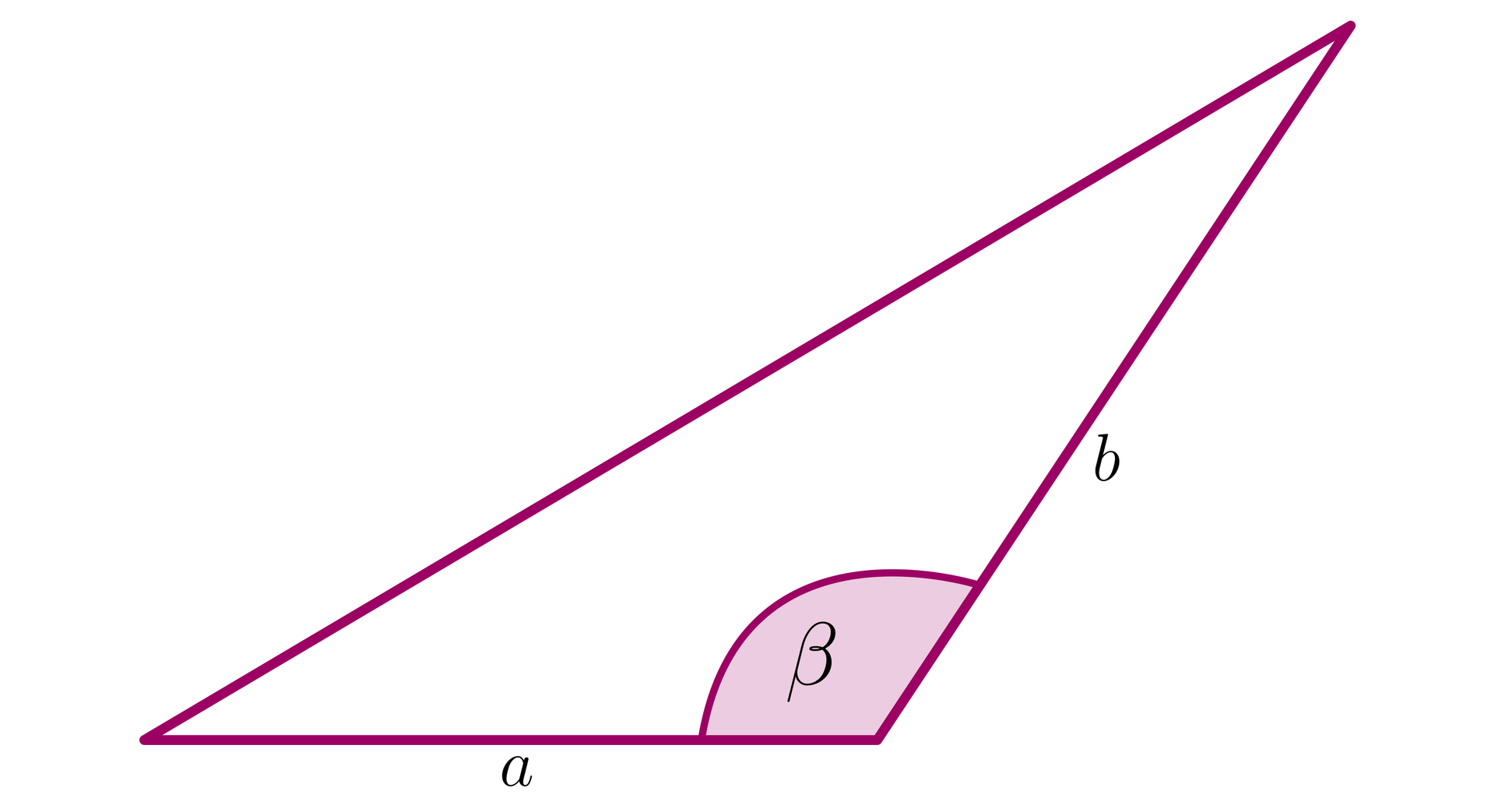
Ilustracja przedstawia trójkąt rozwartokątny. Pomiędzy bokami a i b znajduje się kąt rozwarty beta.

Znasz pojęcie sinusa kąta ostrego, więc umiesz stosować powyższy wzór, gdy kąt $α$ ma nie więcej niż $90 °$ . Spróbujmy zatem zdefiniować sinus kąta rozwartego $β$ , aby także w tym wypadku słuszny był wzór:

$P = \frac{1}{2} a b \sin β$

Twoje cele

Obliczysz sinus, cosinus i tangens kąta rozwartego.

Poznasz zależności między wartościami funkcji trygonometrycznych kątów przyległych.

Wyznaczysz kąt o zadanym sinusie, cosinusie lub tangensie.

Przeczytaj

Sinus, cosinus i tangens kąta rozwartego