Przeczytaj

Przypomnijmy definicje funkcji trygonometrycznych dowolnego kąta.

R1FbrRu22UwcC1

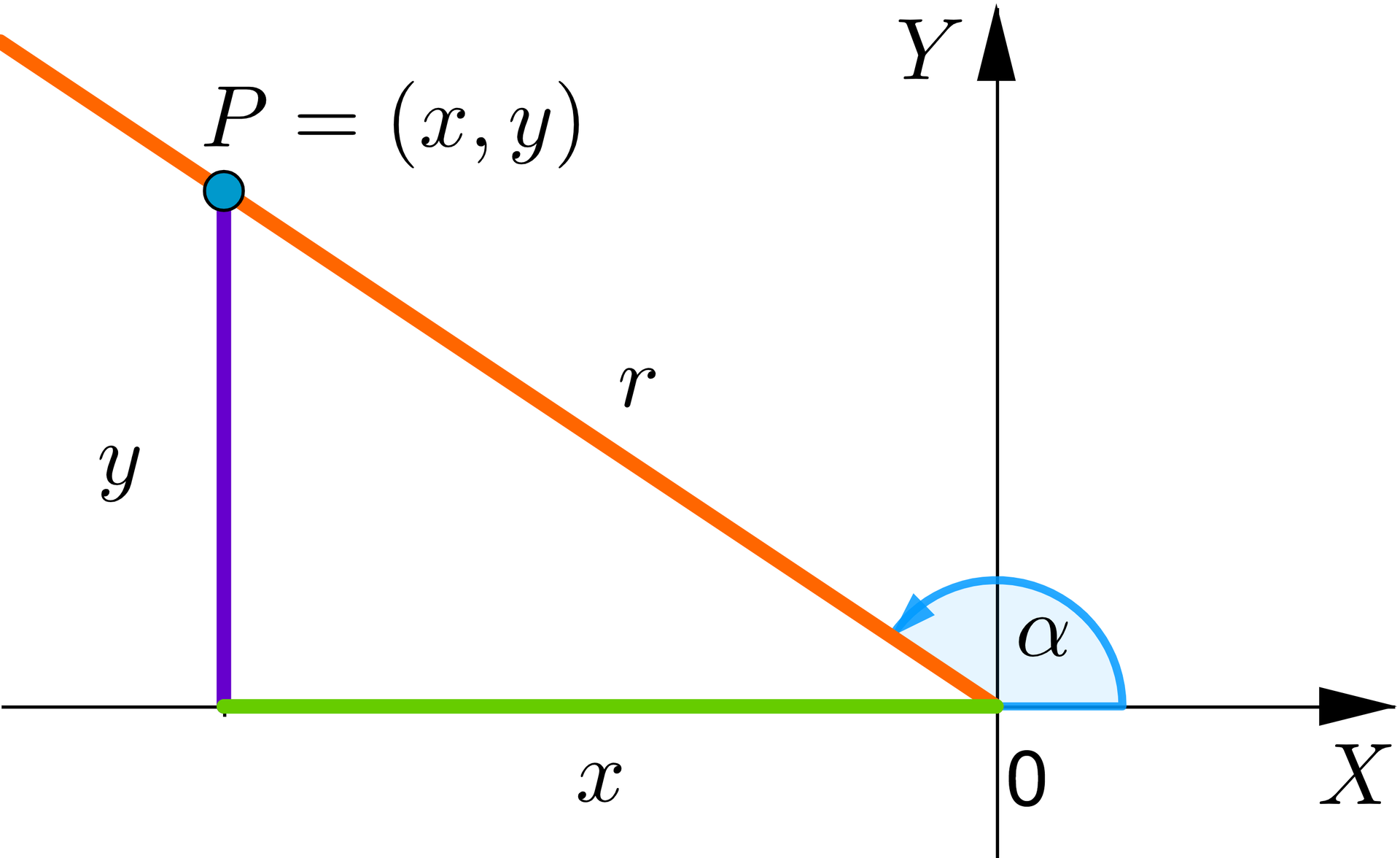
Ilustracja przedstawia układ współrzędnych z poziomą osią x i pionową osią y. W układzie zaznaczono półprostą r, która znajduje się w drugiej ćwiartce i ma swój początek w środku układu współrzędnych i biegnie ukośnie przez punkt P o współrzędnych nawias x średnik y zamknięcie nawiasu. Z punktu P pionowo poprowadzono odcinek do osi x, odcinek ten podpisano literą y. Z punktu przecięcia się odcinka y z osią x poprowadzono poziomy odcinek do początku układu współrzędnych, podpisano go literą x. Pomiędzy osią x a półprostą r zaznaczono kąt rozwarty, podpisano go literą alfa.

$\sin α = \frac{y}{r}$ ,

$\cos α = \frac{x}{r}$ ,

$tg α = \frac{y}{x}$ , gdy $x \neq 0$ ,

gdzie $r = \sqrt{x^{2} + y^{2}} > 0$ jest promieniem wodzącym punktu $P$ .

Przykład 1

Pokażemy, jak wykorzystać trójkąt prostokątny o kątach $30 °$ i $60 °$ do obliczania wartości funkcji trygonometrycznych kąta $150 °$ .

Rozwiązanie

Przyjmijmy, że krótsza przyprostokątna ma długość $1$ , wtedy pozostałe boki mają długości $2$ i $\sqrt{3}$ . Umieścimy ten trójkąt w układzie współrzędnych jak na rysunku.

RCa51z0XrwFPP

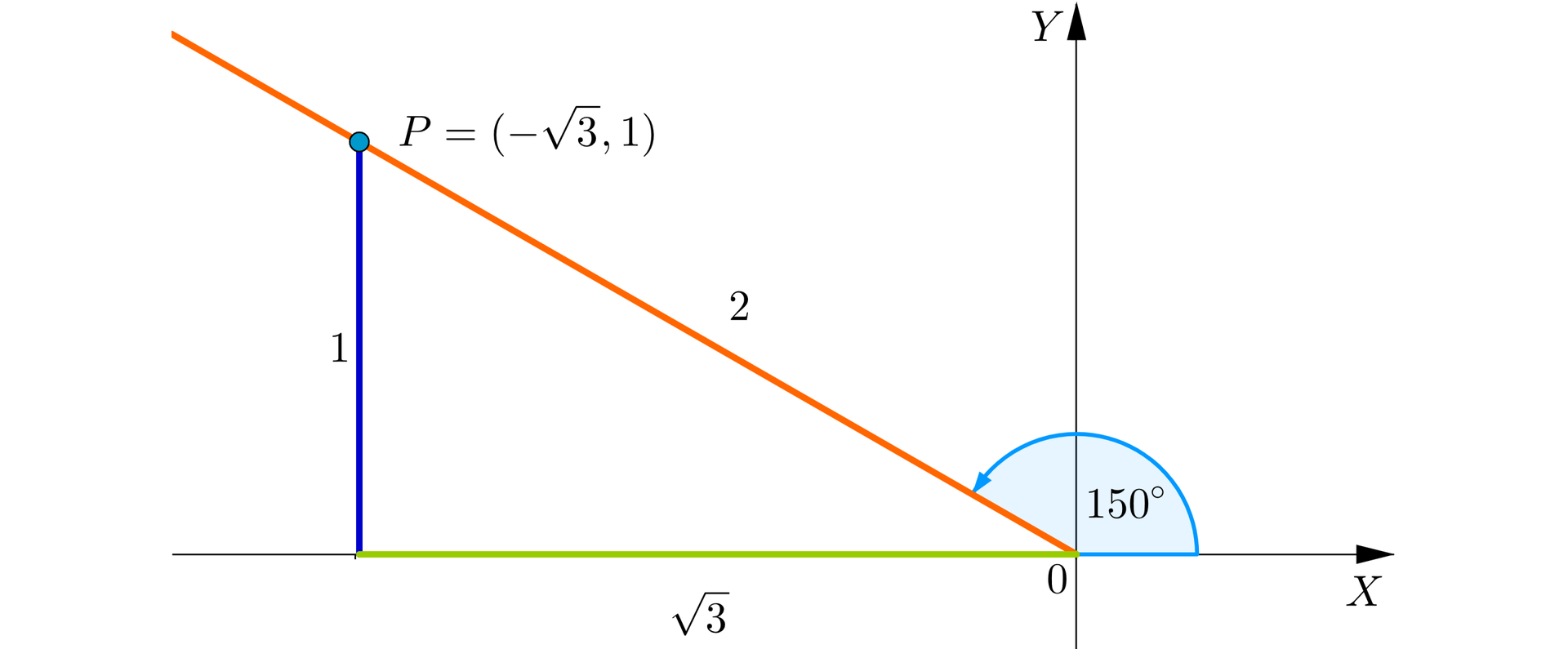
Punkt $P$ ma współrzędne $(- \sqrt{3}, 1)$ , stąd wartości funkcji trygonometrycznych kąta $150 °$ są równe:

$\sin 150 ° = \frac{1}{2}$ ,

$\cos 150 ° = - \frac{\sqrt{3}}{2}$ ,

$tg 150 ° = \frac{1}{- \sqrt{3}} = - \frac{\sqrt{3}}{3}$ .

Zauważmy, że:

$\sin 150 ° = \sin 30 °$

$\cos 150 ° = - \cos 30 °$

$tg 150 ° = - tg 30 °$

Uogólniając powyższą metodę można wykazać, że dla każdego kąta, którego końcowe ramę znajduje się w drugiej ćwiartce układu współrzędnych prawdziwe są równości:

\sin (180^{\circ} - α) = \sin α

\cos (180^{\circ} - α) = - \cos α

tg (180 ° - α) = - tg α

Powyższe równości można też zapisać słownie.

Jeśli $α$ i $β$ są kątami przyległymi to: sinusy kątów przyległych mają równe miary: $\sin α = \sin β$ , cosinusy i tangensy kątów przyległych są liczbami przeciwnymi: $\cos α = - \cos β$ , $tg α = - tg β$ .

Wzór na pole trójkąta

Twierdzenie: Wzór na pole trójkąta

Pole trójkąta o bokach $a$ oraz $b$ i kącie $α$ zawartym między nimi jest równe:

P = \frac{1}{2} a b \sin α

Dowód

Rozważmy dwa trójkąty o bokach $a$ i $b$ oraz kątach przyległych $α$ i $β$ jak na rysunku.

RR2gVPYSvKnVF1

Ilustracja przedstawia trójkąt. Z jednego z wierzchołków poprowadzono odcinek o długości b na jeden z boków, odcinek ten dzieli bok, na który został opuszczony na dwie równe części o długości a. Kąt ostry pomiędzy tym odcinkiem a bokiem podpisano literą alfa, a kąt rozwarty literą beta.

Zauważmy, że pola tych trójkątów są równe, ponieważ podstawy i wysokości obu trójkątów są równe oraz wspólna wysokość wyraża się wzorem $h = b \cdot \sin α$ .

Stąd pole niebieskiego trójkąta wynosi $P = \frac{1}{2} \cdot a \cdot h = \frac{1}{2} \cdot a \cdot b \cdot \sin α$ .

Ponieważ $\sin β = \sin α$ , bo $α = 180 ° - β$ , to pole trójkąta rozwartokątnego wyraża się wzorem $P = \frac{1}{2} a h = \frac{1}{2} a b \cdot \sin α = \frac{1}{2} a b \cdot \sin β$ .

Zauważmy, że jeżeli $α = β = 90 °$ , to $\sin α = \sin β = 1$ , więc pole trójkąta prostokątnego jest równe $P = \frac{1}{2} \cdot a \cdot b \cdot 1 = \frac{1}{2} \cdot a \cdot b \cdot \sin α$ .

Wykazaliśmy, że pole każdego trójkąta jest równe połowie iloczynu boków trójkąta oraz sinusa kąta zwartego między nimi.

Jedynka trygonometryczna

Twierdzenie: Jedynka trygonometryczna

Dla dowolnego kąta $0 ° \leq β \leq 180 °$ zachodzi równość:

\sin^{2} β + \cos^{2} β = 1

Dowód

Jeśli $β$ jest kątem ostrym, to twierdzenie wynika bezpośrednio z twierdzenia Pitagorasa.

Jeśli $β = 90 °$ , to $\sin^{2} β + \cos^{2} β = \sin^{2} 90 ° + \cos^{2} 90 ° = 1 + 0 = 1$ .

Jeśli natomiast $β$ jest kątem rozwartym, to niech $α$ będzie kątem ostrym do niego przyległym. Wtedy:

$\sin^{2} β + \cos^{2} β = {(\sin α)}^{2} + (- \cos α)^{2} = \sin^{2} α + \cos^{2} α = 1$ .

Przykład 2

R1RsnZDqkaYk31

Ilustracja przedstawia trójkąt. Z jednego z wierzchołków poprowadzono odcinek na jeden z boków, Kąt ostry pomiędzy tym odcinkiem a bokiem ma miarę 60 stopni, a kąt rozwarty ma miarę 120 stopni.

Obliczymy $\sin 120 °$ i $\cos 120 °$ .

Rozwiązanie

Jeśli $β = 120 °$ , to kąt do niego przyległy ma miarę $α = 60 °$ , zatem otrzymujemy:

$\sin 120 ° = \sin 60 ° = \frac{\sqrt{3}}{2}$ , $\cos 120 ° = - \cos 60 ° = - \frac{1}{2}$ .

Przykład 3

Wyrazimy wartości funkcji $\sin 137 °$ i $\cos 137 °$ za pomocą odpowiednich wartości funkcji kąta ostrego.

Rozwiązanie

Jeśli $β = 137 °$ , to kąt do niego przyległy $α = 43 °$ i mamy:

$\sin 137 ° = \sin 43 °$ , $\cos 137 ° = - \cos 43 °$ .

Przykład 4

Znajdziemy kąt wypukłykąt wypukłykąt wypukły $β$ , którego cosinus jest równy $- \frac{\sqrt{3}}{2}$ .

Rozwiązanie

Kąt $β$ musi być rozwarty, bo jego cosinus jest ujemny. Zgodnie z definicją cosinusa kąta rozwartego:

$\cos β = - \cos α$ ,

gdzie $α$ to kąt przyległy do $β$ . Poszukajmy więc takiego kąta ostrego $α$ , że:

$\cos α = \frac{\sqrt{3}}{2}$ .

Takim kątem jest $α = 30 °$ . Stąd poszukiwany kąt $β$ jest równy $150 °$ .

Przykład 5

Wyznaczymy pole trójkąta o bokach $a = 6$ , $b = 4$ oraz kącie między nimi $β = 135 °$ .

Rozwiązanie

Kąt ostry przyległy do $β$ jest równy $α = 45 °$ , więc:

$P = \frac{1}{2} a b \sin β = \frac{1}{2} a b \sin α = \frac{1}{2} \cdot 6 \cdot 4 \cdot \sin 45 ° = 12 \cdot \frac{\sqrt{2}}{2} = 6 \sqrt{2}$

Tangens kąta

Dla dowolnego kąta wypukłegokąt wypukłykąta wypukłego różnego od kąta prostego zachodzi tożsamość:

tg α = \frac{\sin α}{\cos α}

Ważne!

Dla kąta prostego tangens nie jest określony, gdyż nie wolno dzielić przez zero $(\cos 90 ° = 0)$ .

Jeśli $β$ jest kątem rozwartym przyległym do kąta ostrego $α$ , to:

tg β = \frac{\sin β}{\cos β} = \frac{\sin α}{- \cos α} = - tg α

Tangens kąta rozwartego jest zatem równy liczbie przeciwnej do tangensa kąta ostrego do niego przyległego. W związku z tym tangens dowolnego kąta rozwartego jest liczbą ujemną.

Przykład 6

Obliczymy tangens kąta $β = 120 °$ .

Rozwiązanie

Kąt ostry przyległy do $β$ ma miarę $α = 60 °$ , więc:

$tg 120 ° = - tg 60 ° = - \sqrt{3}$ .

Przykład 7

Znajdziemy kąt wypukłykąt wypukłykąt wypukły $β$ taki, że:

$tg β = - 1$

Rozwiązanie

Ponieważ tangens jest ujemny, więc kąt wypukły $β$ musi być rozwartykąt rozwartyrozwarty. Poszukajmy najpierw kąta ostrego $α$ przyległego do $β$ . Wtedy:

$tg α = - tg β = 1$

Stąd $α = 45 °$ . A zatem $β = 180 ° - α = 180 ° - 45 ° = 135 °$ .

Słownik

kąty przyległe

kąty, które mają wspólne ramię i tworzą razem kąt półpełny

kąt rozwarty

ma miarę większą niż $90 °$ i mniejszą niż $180 °$

kąt wypukły

ma miarę większą niż $0 °$ i mniejszą lub równą $180 °$ . Kąty: ostry, prosty, rozwarty i półpełny są kątami wypukłymi

Wprowadzenie

Infografika

Słownik