O podziale na trójkąty sześciokąta gwiaździstego foremnego

Dla danego $n$–kąta foremnego możemy rozważyć łamaną zamkniętą o $n$ wierzchołkach, utworzoną z tych przekątnych tego wielokąta, które mają równą długość – otrzymujemy wówczas wielokąt foremny gwiaździsty.

Tak zdefiniowane pojęcie można uogólnić i dopuścić możliwość nakładanie się wielokątów zbudowanych z przekątnych równej długości. Wówczas sześciokątem gwiaździstym foremnym nazwiemy figurę, która powstanie w wyniku nałożenia na siebie dwóch trójkątów równobocznych, jak na rysunku.

RH3Bgp08d78T2

Na ilustracji przedstawiono sześciokąt foremny $ABCDEF$. Zielonym kolorem zacieniowano trójkąt powstały po połączeniu wierzchołków A, C, E. Fioletowym kolorem zacieniowano trójkąt powstały po połączeniu wierzchołków B, D, F.

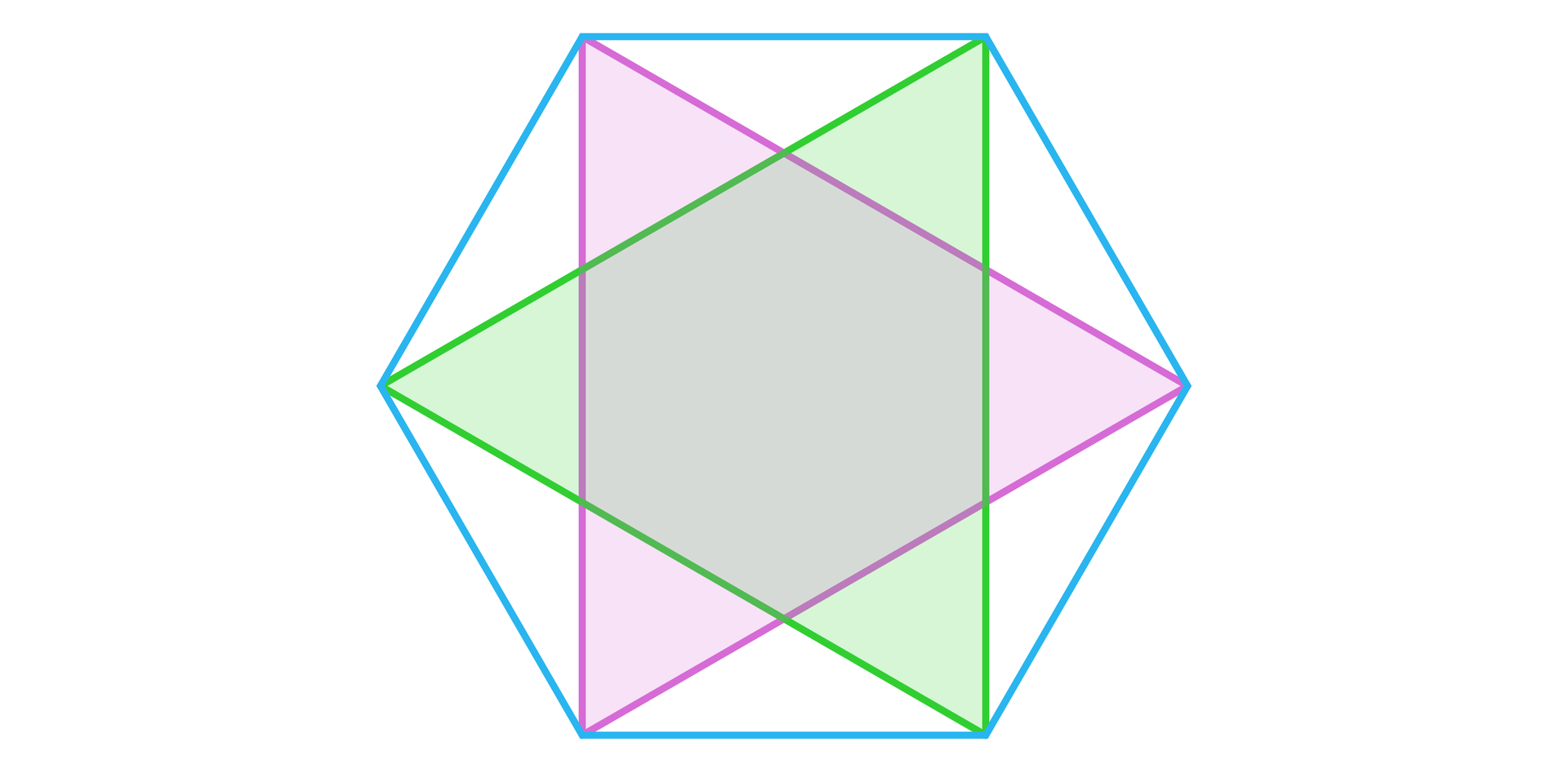
Poprowadzimy teraz przekątne wyjściowego sześciokąta oraz przekątne sześciokąta, którego wierzchołkami są punkty przecięcia trójkątów wyznaczających sześciokąt gwiaździsty.

R1Oc4TnPgRUnn

Na ilustracji przedstawiono sześciokąt foremny $ABCDEF$. Zielonym kolorem zacieniowano trójkąt powstały po połączeniu wierzchołków A, C, E. Fioletowym kolorem zacieniowano trójkąt powstały po połączeniu wierzchołków B, D, F. Trójkąty nakładając się, tworzą sześciokąt gwiaździsty. Poprowadzono przekątne wyjściowego sześciokąta, oraz przekątne sześciokąta, którego wierzchołkami są punkty przecięcia trójkątów.

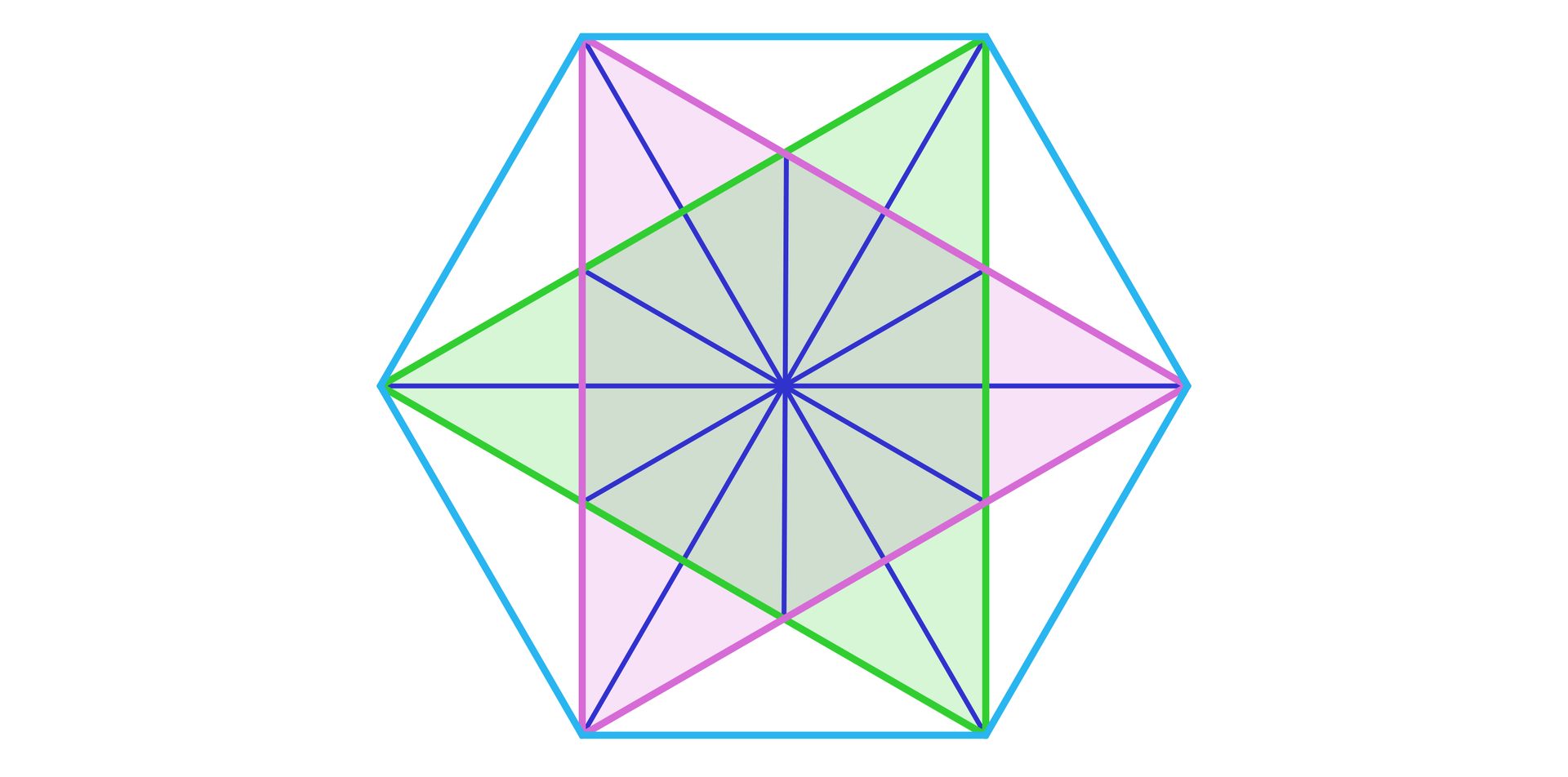
Odcinki te podzieliły figurę na przystające trójkąty prostokątne – ich przystawanie pozwala łatwo wyznaczać związki miarowe między bokami wyjściowego sześciokąta foremnego i sześciokątem gwiaździstym. Przystawanie trójkątów prostokątnych jest tematem tego materiału.