Przeczytaj

Trójkąty przystające

Wiemy, że trójkąty są przystające, gdy ich odpowiednie boki mają równe długości i odpowiednie kąty mają równe miary. Oznacza to, że przystawanie trójkątów jest zdefiniowane poprzez równości trzech par boków oraz trzech par odpowiednich kątów – tym samym definicja wymaga jednoczesnego spełnienia sześciu warunków. Znamy jednak podstawowe twierdzenia ustalające warunki równoważne przystawaniu trójkątów, w których wystarczy zbadać trzy spośród sześciu warunków – są to cechy przystawania trójkątówcechy przystawania trójkątówcechy przystawania trójkątów.
Pierwsza z cech orzeka, że trójkąty są przystające, jeśli boki jednego trójkąta są równe odpowiednim bokom w drugim trójkącie (cecha bok – bok – bok, krótko bbb).
Druga cecha stwierdza, że trójkąty są przystające, jeśli dwa boki jednego trójkąta są równe odpowiednim dwóm bokom drugiego trójkąta i kąty zawarte między tymi parami boków w obu trójkątach są równe (cecha bok – kąt – bok, krótko bkb).
Wreszcie trzecia cecha (kąt – bok – kąt, krótko kbk) stwierdza, że trójkąty są przystające, jeśli jeden bok pierwszego trójkąta i kąty przyległe do tego boku są równe odpowiednio bokowi i kątom przyległym do tego boku w drugim trójkącie.

Przystawanie trójkątów prostokątnych

Pokażemy, że w trójkącie prostokątnym te cechy można sformułować jeszcze inaczej. Udowodnimy na wstępie poniższe twierdzenie

Pierwsza cecha przystawania trójkątów prostokątnych

Twierdzenie: Pierwsza cecha przystawania trójkątów prostokątnych

Jeżeli przeciwprostokątna i jedna z przyprostokątnych jednego trójkąta są odpowiednio równe przeciwprostokątnej i jednej z przyprostokątnych drugiego trójkąta, to trójkąty te są przystające.

Dowód

Rozważmy trójkąty prostokątne $A B C$ oraz $A' B' C'$ , o kątach prostych przy wierzchołkach odpowiednio $B$ i $B'$ , takie, że $|A C| = |A' C'|$ oraz $|A B| = |A' B'|$ . Rozważmy takie położenie tych trójkątów, w którym wierzchołki $A$ i $A'$ , oraz $B$ i $B'$ , się pokrywają, jak na rysunku.

R1JVhi6GqOpAa

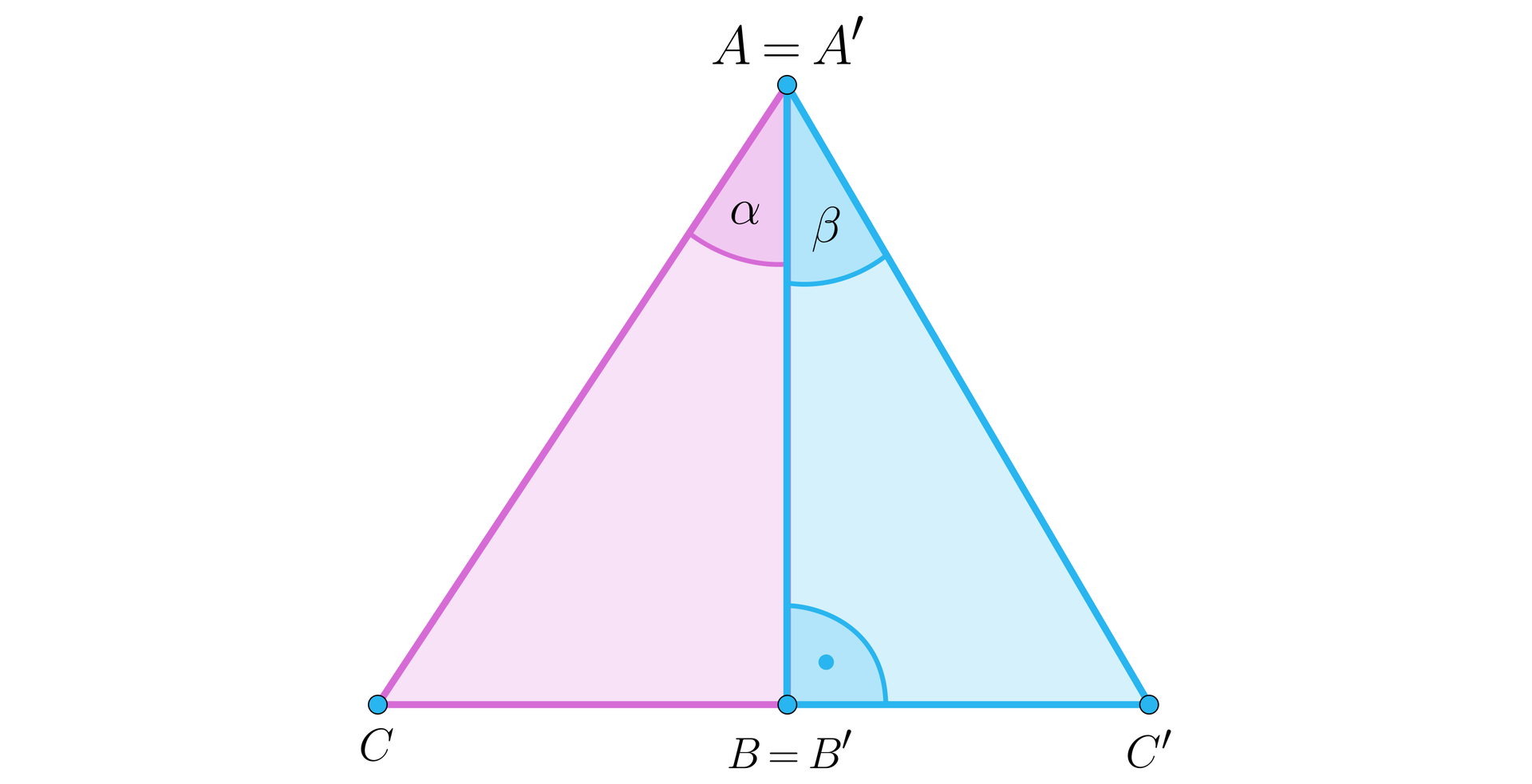
Na ilustracji przedstawiono trójkąty prostokątne ABC, oraz A'B'C'. Trójkąty są ułożone w taki sposób, że wierzchołki A i A', oraz B i B' się pokrywają. Kąt CAB jest równy alfa. Kąt C'A'B' jest równy beta. — Pierwsza cecha przystawania trójkątów prostokątnych

Zauważmy, że wówczas $|∢ C B A| + |∢ A B C| = 180 °$ , co oznacza, że punkty $C$ , $B$ , $C'$ są współliniowe, a punkty $C$ , $A$ , $C'$ są wierzchołkami trójkąta równoramiennego o wysokości $A B$ . Ponieważ w trójkącie równoramiennym $C A C'$ wysokość $A B$ jest jednocześnie dwusieczną kąta $∢ C A C'$ , więc $α = β$ . Zatem $△ A B C \equiv △ A' B' C'$ na mocy cechy bkb przystawania trójkątów (dowolnych).

Druga cecha przystawania trójkątów prostokątnych

Twierdzenie: Druga cecha przystawania trójkątów prostokątnych

Jeżeli dwie przyprostokątne jednego trójkąta są odpowiednio równe dwóm przyprostokątnym drugiego trójkąta, to trójkąty te są przystające.

Dowód

Rozważmy trójkąty prostokątne $A B C$ oraz $A' B' C'$ , o kątach prostych przy wierzchołkach odpowiednio $B$ i $B'$ , takie, że $|B C| = |B' C'|$ oraz $|A B| = |A' B'|$ . Zauważmy, że ponieważ kąty między parami przyprostokątnych (kąty proste) są odpowiednio równe w obu trójkątach, to na mocy cechy bkb przystawania trójkątów (dowolnych) mamy, że $△ A B C \equiv △ A' B' C'$ .

Trzecia cecha przystawania trójkątów prostokątnych

Twierdzenie: Trzecia cecha przystawania trójkątów prostokątnych

Jeżeli przyprostokątna i jeden z kątów ostrych jednego trójkąta są odpowiednio równe przyprostokątnej i jednemu z kątów ostrych drugiego trójkąta, to trójkąty te są przystające.

Dowód

Rozważmy trójkąty prostokątne $A B C$ oraz $A' B' C'$ , o kątach prostych przy wierzchołkach odpowiednio $B$ i $B'$ , takie, że $|A B| = |A' B'|$ oraz $|∢ B A C| = |∢ B' A' C'|$ , jak na rysunku.

RbGzJLebDqENs

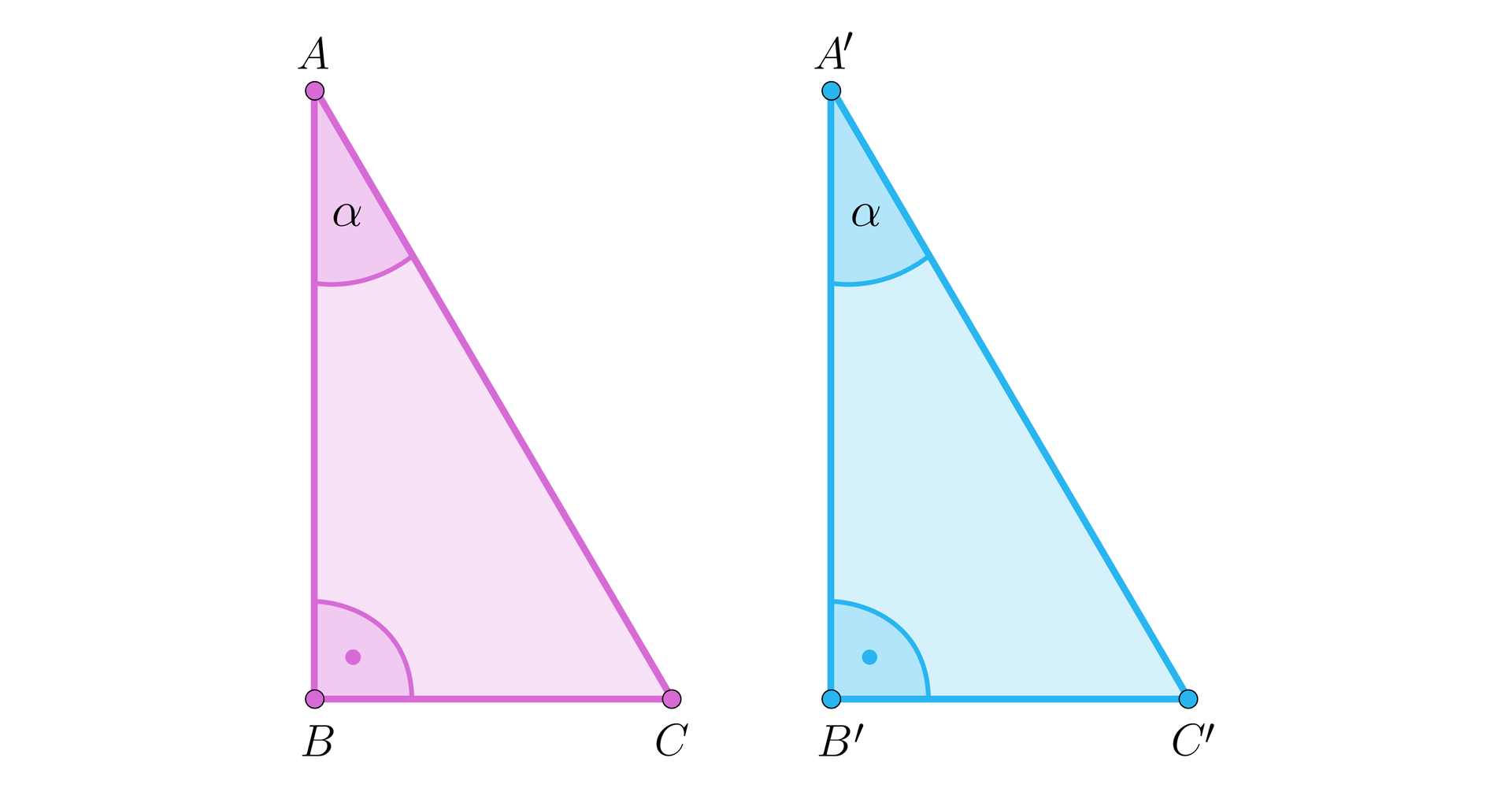
Na ilustracji przedstawiono dwa trójkąty prostokątne ABC, oraz A'B'C'. Kąty proste znajdują się przy wierzchołkach odpowiednio B i B'. Kąty przy wierzchołkach A, oraz A' oznaczono alfa. — Trzecia cecha przystawania trójkątów prostokątnych

Zauważmy, że wówczas przy równych bokach $A B$ oraz $A' B'$ pary kątów przyległych są odpowiednio równe. Zatem na mocy cechy kbk przystawania trójkątów (dowolnych) mamy, że $△ A B C \equiv △ A' B' C'$ .

Czwarta cecha przystawania trójkątów prostokątnych

Twierdzenie: Czwarta cecha przystawania trójkątów prostokątnych

Jeżeli przeciwprostokątna i jeden z kątów ostrych jednego trójkąta są odpowiednio równe przeciwprostokątnej i jednemu z kątów ostrych drugiego trójkąta, to trójkąty te są przystające.

Dowód

Zauważmy, że teza wynika natychmiast z cechy kbk przystawania trójkątów (dowolnych), jak w poprzednim dowodzie.

Przykład 1

Rozważmy trójkąt $A B C$ , w którym $|B C| = 3$ oraz $|A C| = 4$ . Na boku $A B$ leżą wierzchołki $E$ , $F$ prostokąta, którego dwa pozostałe wierzchołki leżą odpowiednio na pozostałych bokach danego trójkąta, jak na rysunku.

RoGd3nKsuQ9AH

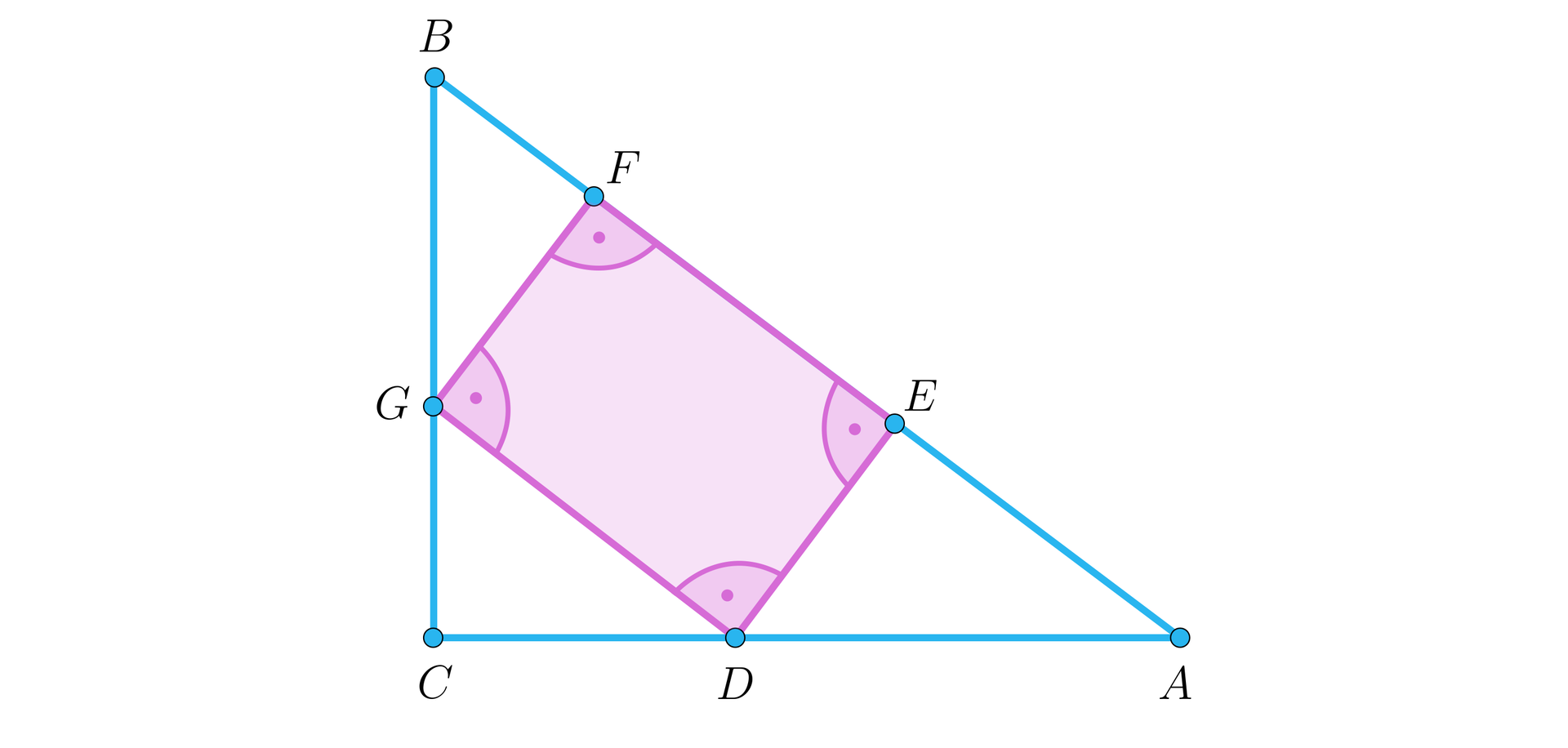
Na ilustracji przedstawiono trójkąt prostokątny ABC. Na przyprostokątnej AC zaznaczono punkt D. Na przyprostokątnej BC zaznaczono punkt G. Na przeciwprostokątnej AB zaznaczono punkt F oraz punkt E. Punkty zaznaczono w taki sposób, że po ich połączeniu powstał prostokąt, który zacieniowano.

Wyznaczymy pole prostokąta $D E F G$ , jeśli $△ G F B \equiv △ D C G$ .

Rozwiązanie:

Na wstępie zauważmy, że trójkąt $D C G$ jest trójkątem prostokątnym, ponieważ trójkątem prostokątnym jest trójkąt $G F B$ . Zatem jeden z jego kątów jest prosty i musi to być kąt przy wierzchołku $C$ . Ale to oznacza oczywiście, że trójkąt $A B C$ także jest trójkątem prostokątnym o przeciwprostokątnej równej $5$ . Zauważmy, że trójkąt $A B C$ oraz trójkąty $A D E$ , $D G C$ oraz $G B F$ są podobne.

Przyjmijmy $|B G| = x = |D G| = |E F|$ , wtedy: $|C G| = 3 - x = |B F|$ oraz $|G F| = \frac{4}{5} x = |D E|$ .

Z podobieństw odpowiednich trójkątów wynika także, że $\frac{|D E|}{|A E|} = \frac{3}{4}$ , stąd $|A E| = \frac{4}{3} \cdot (\frac{4}{5} x) = \frac{16}{15} x$ .

Ponieważ $|A E| + |E F| + |B F| = |A B| = 5$ , więc $\frac{16}{15} x + x + (3 - x) = 5$ .

Stąd $x = \frac{15}{8}$ , a pole prostokąta jest równe $\frac{15}{8} \cdot (\frac{4}{5} \cdot \frac{15}{8}) = \frac{45}{16}$ .

Pole a przystawanie trójkątów

Przypuśćmy, że dane są dwa trójkąty o równych polach, w których jeden z boków jednego trójkąta jest równy bokowi w drugim trójkącie. Oczywiście tak zadane warunki nie są warunkiem wystarczającym, by trójkąty te były przystające, co łatwo zauważyć analizując poniższy rysunek.

RVLm2JdoHB3RD

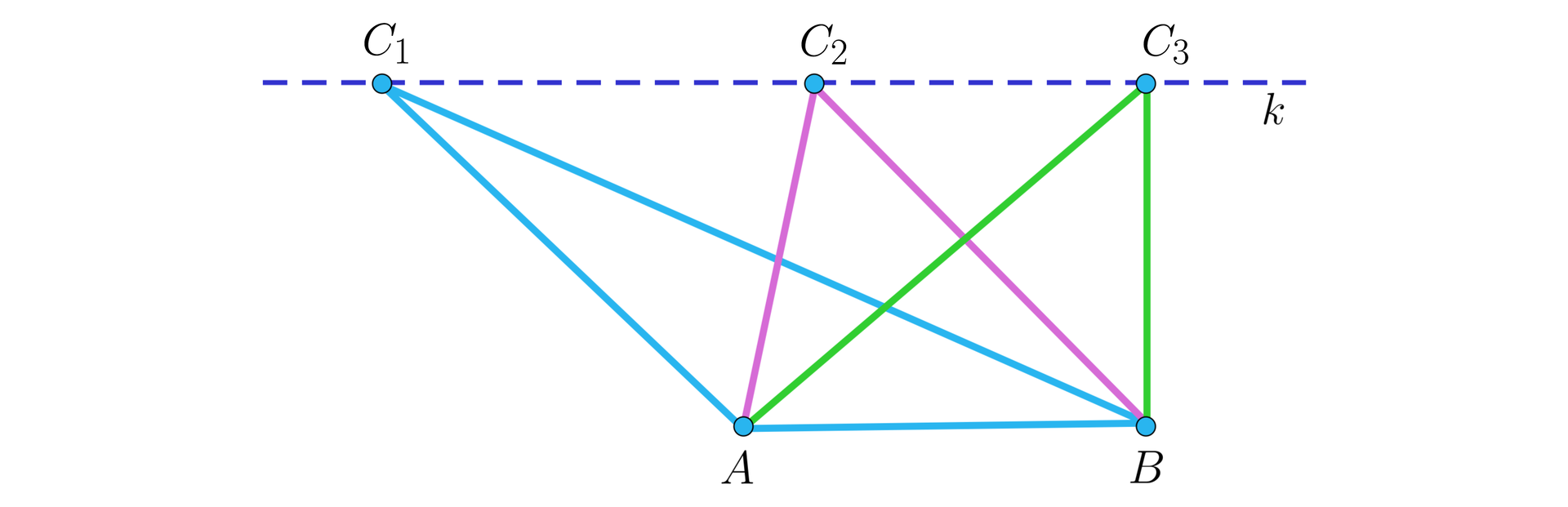
Na ilustracji przedstawiono przerywaną prostą k, na której zaznaczono trzy punkty, C1, C2, oraz C3. Poniżej, znajdują się dwa współliniowe punkty A i B. Punkty na prostej, oraz punkty A i B, połączono w taki sposób, że powstały trzy trójkąty o wierzchołkach C1, C2, C3 i wspólnej podstawie AB. — Pole a przystawanie trójkątów

Jeśli prosta $k$ jest równoległa do podstawy $A B$ każdego z narysowanych trójkątów, a różne wierzchołki $C_{1}$ , $C_{2}$ , $C_{3}$ leżą na tej prostej, to pola trójkątów $A C_{1} B$ , $A C_{2} B$ oraz $A C_{3} B$ są równe. Jednocześnie widać, że te trójkąty nie mogą być przystające (byłoby to możliwe dla dwóch spośród takiej trójki trójkątów, które byłyby symetryczne względem symetralnej podstawy $A B$ ).

Jednak w przypadku trójkątów prostokątnych jest inaczej. Oczywiście, jeśli dwa trójkąty mają po jednej przyprostokątnej równej długości i oba te trójkąty mają równe pola, to stąd wynika natychmiast równość także drugich przyprostokątnych, co na mocy drugiej cechy przystawania trójkątówcechy przystawania trójkątówcechy przystawania trójkątów prostokątnych pozwala stwierdzić, że takie trójkąty są przystające. Zajmiemy się więc poniżej przypadkiem nieco trudniejszym.

Przykład 2

Pokażemy, że jeśli dwa trójkąty prostokątne o równych przeciwprostokątnych mają równe pola, to są przystające.

Rozwiązanie:

Rozważmy trójkąty prostokątne $A B C$ i $A_{1} B_{1} C_{1}$ , o kątach prostych odpowiednio przy wierzchołkach $C$ oraz $C_{1}$ i takie, że przeciwprostokątne mają równe długości, czyli $|A B| = |A_{1} B_{1}|$ .

Rozważmy takie położenie tych trójkątów, by $A = A_{1}$ oraz $B = B_{1}$ , a wierzchołki $C$ oraz $C_{1}$ leżały po jednej stronie prostej $A B$ .

Równość pól obu oznacza, że wierzchołki $C$ oraz $C_{1}$ leżą w tej samej odległości od prostej $A B$ , czyli na pewnej prostej $k$ równoległej do $A B$ , jak na rysunku.

R1D2oWePN4WKs

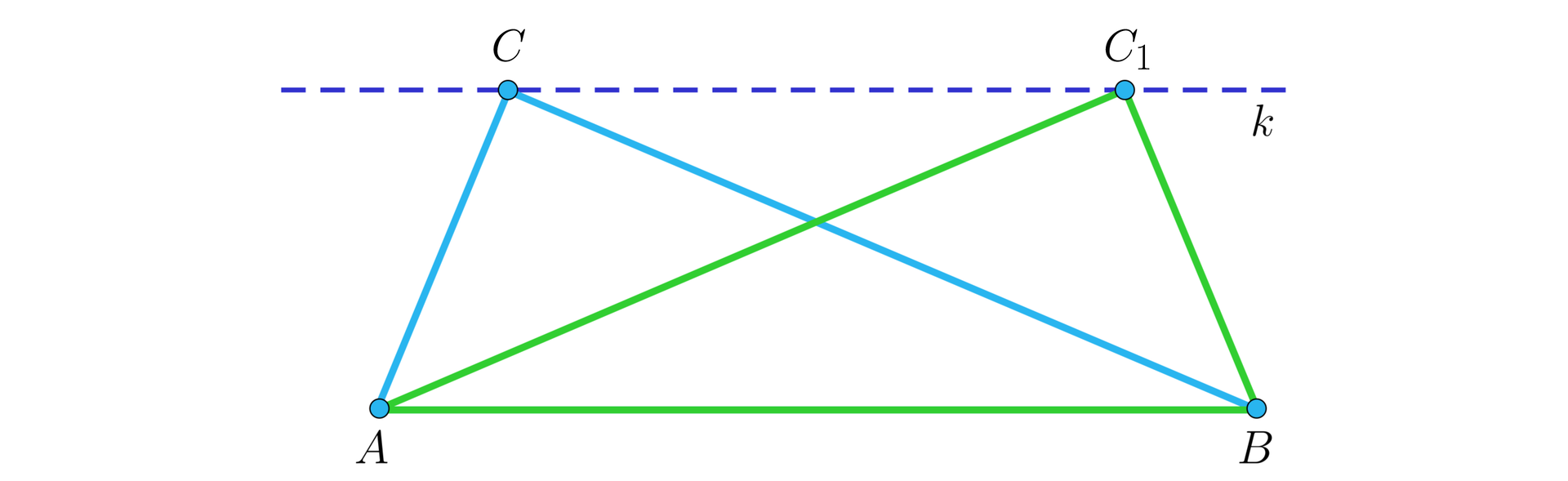
Na ilustracji przedstawiono przerywaną prostą k. Na prostej zaznaczono punkt C, oraz C1. Poniżej zaznaczono dwa współliniowe punkty A i B. Zieloną linią połączono punkty A, B oraz C1. Linią niebieską połączono punkty ABC. — Pole a przystawanie trójkątów prostokątnych

Jeśli $C = C_{1}$ to przystawanie odpowiednich trójkątów jest oczywiste.

Przypuśćmy więc, że punkty $C$ , $C_{1}$ są różne. Wiemy, że każdy trójkąt prostokątny można wpisać w okrąg, którego średnicą jest przeciwprostokątna. Zatem wierzchołki kąta prostego muszą leżeć zarówno na prostej $k$ , jak i na okręgu, którego średnicą jest bok $A B$ . Tym samym istnieją co najwyżej dwa takie punkty (wspólne prostej i okręgu). Dołączmy zatem do rysunku okrąg o średnicy $A B$ i środku $O$ .

RQIy72YA4DguP

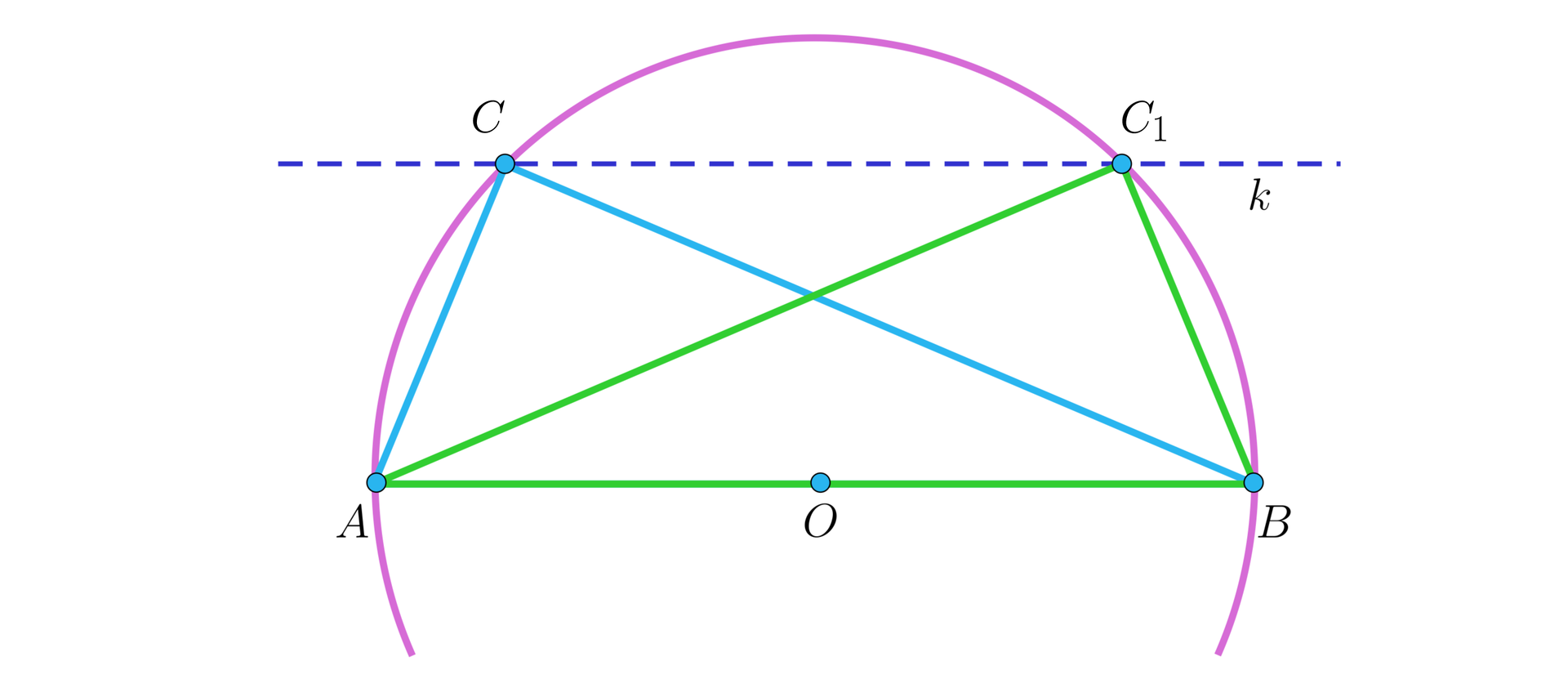
Na ilustracji przedstawiono okrąg o środku w punkcie O. Na okręgu zaznaczono punkt C, i C1, które leżą na prostej k. Średnica AB jest równoległa do prostej k. Zieloną linią połączono punkty A, B i C1. Niebieską linią połączono punkty A, B i C. — Pole a przystawanie trójkątów prostokątnych – dowód

Pozostaje teraz przywołać twierdzenie dotyczące geometrii w okręgu:

w każdym okręgu kąty wpisane oparte na tym samym łuku mają równe miary;

równe miary mają kąty wpisane oparte na dwóch łukach równej długości;

jeżeli łuki tego samego okręgu są równej długości, to odpowiadające im cięciwy są także równej długości.

Proste $A B$ i $C C_{1}$ są równoległe wtedy i tylko wtedy, gdy $|∢ B A C_{1}| = |∢ A C_{1} C_{}|$ , ale to oznacza (patrz powyższe stwierdzenia), że w szczególności $|A C_{}| = |B C_{1}|$ . Zatem na mocy pierwszej cechy przystawania trójkątów prostokątnych (równość przeciwprostokątnych i jednej pary przyprostokątnych) mamy $△ A B C \equiv △ A_{1} B_{1} C_{1}$ .

Słownik

cechy przystawania trójkątów

zestaw twierdzeń określających warunki równoważne występowania relacji przystawania między dwoma trójkątami

Wprowadzenie

Aplet

Trójkąty przystające

Przystawanie trójkątów prostokątnych

Pole a przystawanie trójkątów

Słownik