Aplet

Polecenie 1

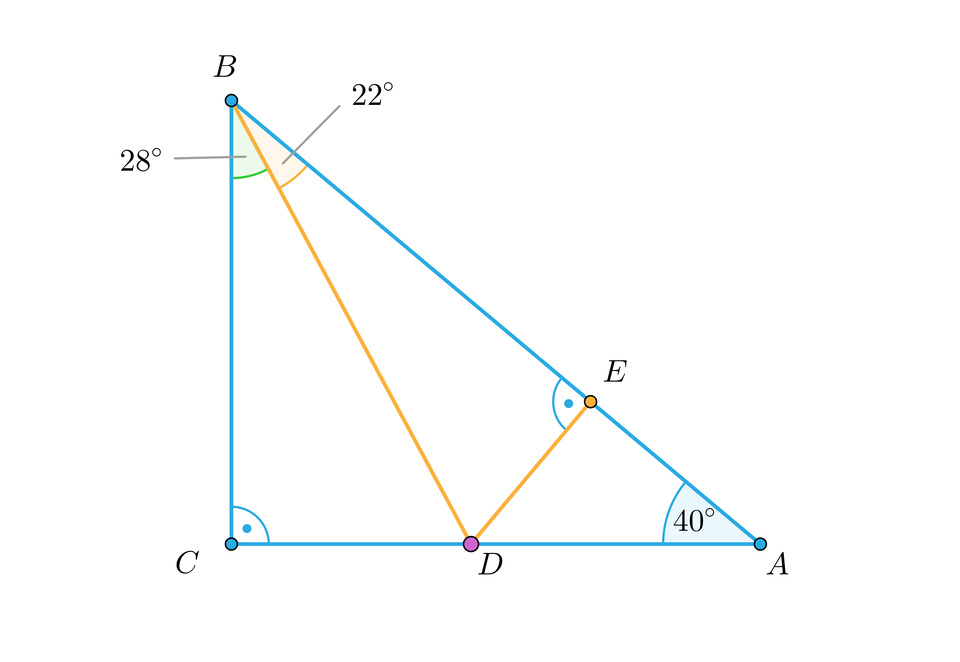
Uruchom aplet. Zmieniaj położenie wyróżnionego punktu $D$ leżącego na przyprostokątnej $A C$ trójkąta prostokątnego $A B C$ w taki sposób, aby dwa spośród trójkątów $C B D$ , $E B D$ oraz $E A D$ , na które podzielony jest trójkąt $A B C$ były przystające.

R1DKw6ZNsqoTL

Polecenie 2

Wyznacz wszystkie wartości miary kąta $D B E$ , dla których dwa spośród trójkątów $C B D$ , $E B D$ oraz $E A D$ są przystające.

Zauważmy, że w przypadku, gdy $△ E A D \equiv △ E B D$ , to $|∢ D B E| = 40 °$ .

W przypadku, gdy $△ C B D \equiv △ E B D$ , to odcinek $B D$ musi zawierać się w dwusiecznej kąta $A B C$ , czyli $|∢ D B E| = 25 °$ .

Polecenie 3

Rozważmy trójkąt prostokątny o przeciwprostokątnej $A B$ . Punkty $D$ oraz $E$ leżą odpowiednio na przyprostokątnej $A C$ oraz przeciwprostokątnej $A B$ w taki sposób, że odcinek $D E$ jest prostopadły do boku $A B$ . Wyznacz kąty tego trójkąta, jeśli $△ E A D \equiv △ E B D \equiv △ C B D$ .

Zauważmy, że $△ E A D \equiv △ E B D$ , wtedy, gdy $|∢ D B E| = |∢ D A E|$ .

Z kolei $△ C B D \equiv △ E B D$ wtedy, gdy $|∢ D B E| = |∢ C B D|$ .

Ale $|∢ D B E| + |∢ C B D| + |∢ D A E| = 90 °$ .

Stąd $|∢ D B E| = |∢ C B D| = |∢ D A E| = 30 °$ oraz $|∢ A B C| = 60 °$ .

Przeczytaj

Sprawdź się