Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

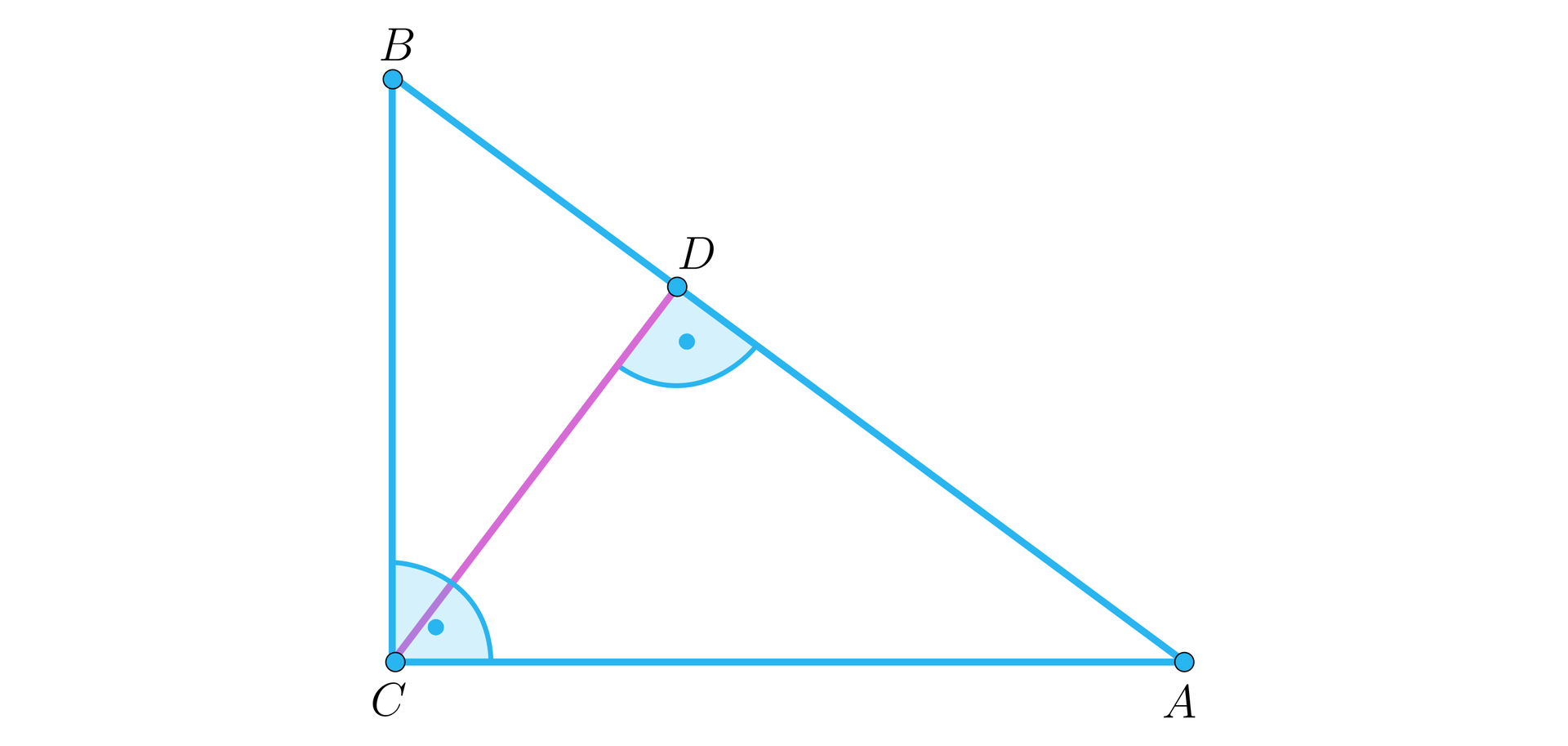
Uzasadnij, że jeśli wysokość trójkąta prostokątnego $A B C$ , poprowadzona z wierzchołka kąta prostego, dzieli ten trójkąt na dwa trojkąty o równych polach, to trójkąt $A B C$ jest równoramienny.

Przyjmijmy oznaczenia, jak na rysunku.

RdMWosHFfNLp1

Na ilustracji przedstawiono trójkąt prostokątny o przyprostokątnych AC, BC, oraz przeciwprostokątnej AB. Na przeciwprostokątnej AB, zaznaczono punkt D, który połączono z wierzchołkiem A. Kąt CDA jest kątem prostym.

Trójkąty $C D A$ oraz $C D B$ mają wspólną przyprostokątną $C D$ . Z równości ich pól (pole trójkąta prostokątnego jest połową iloczynu długości przyprostokątnych) wynika, że $|B D| = |A D|$ . Zatem na mocy drugiej cechy przystawania trójkątów prostokątnych mamy, że $△ A D C \equiv △ B D C$ . Stąd w szczególności wynika równość kątów $C A D$ oraz $C B D$ . To kończy dowód.

Ćwiczenie 2

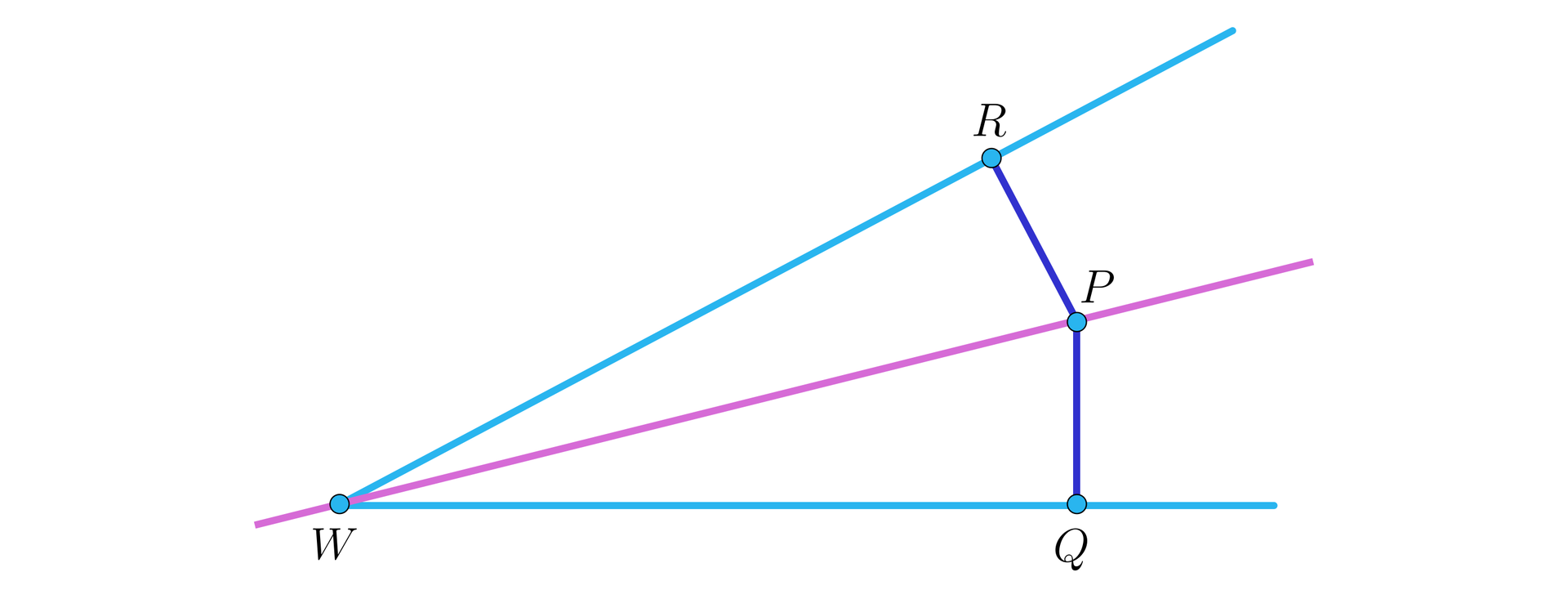
Wykaż, że dwusieczna kąta jest zbiorem punktów równo odległych od jego ramion.

Rozważmy dowolny kąt o wierzchołku w punkcie $W$ i poprowadźmy jego dwusieczną, jak na rysunku.

RlvV7c1iIIgRZ

Na ilustracji przedstawiono kąt o wierzchołku w punkcie W. Na jego ramionach zaznaczono punkty R, oraz Q. Poprowadzono dwusieczną kąta, na której zaznaczono punkt P. Połączono punkt R, P oraz Q.

Niech $P$ będzie dowolnym punktem leżącym na tej dwusiecznej. Rozważmy punkty $Q$ , $R$ leżące odpowiednio na ramionach kąta, takie, że $|∢ W R P| = |∢ W Q P| = 90 °$ . Wtedy trójkąty $W Q P$ oraz $W R P$ są trójkątami o wspólnej przeciwprostokątnej, w których jeden z kątów ostrych ma taką samą miarę. Na mocy czwartej cechy przystawania trójkątów prostokątnych, trójkąty te są przystające. W szczególności $|P Q| = |P R|$ . To kończy dowód.

RNPnmxL4Izj9O1

Ćwiczenie 3

Zaznacz poprawną odpowiedź. Boki trójkąta prostokątnego $A B C$ mają odpowiednio długości $5$ , $12$ , $13$ . Trójkąt $D E F$ jest przystający do trójkąta $A B C$ . Jeden z boków trójkąta $D E F$ ma długość:

$\sqrt{12 - 6 \sqrt{3}} + \sqrt{12 + 6 \sqrt{3}}$
$\sqrt{12 - 6 \sqrt{3}} - \sqrt{12 + 6 \sqrt{3}}$
$\sqrt{48 + 24 \sqrt{3}} + \sqrt{48 - 24 \sqrt{3}}$
$\sqrt{48 + 24 \sqrt{3}} - \sqrt{48 - 24 \sqrt{3}}$

Ćwiczenie 4

Rozważmy trójkąt prostokątny $A B C$ , o przeciwprostokątnej $A B$ długości $12$ . Na boku $A B$ leżą wierzchołki $E$ , $F$ kwadratu o polu równym $16$ , którego dwa pozostałe wierzchołki leżą odpowiednio na pozostałych bokach danego trójkąta, jak na rysunku.

RHSVlP5gmVx4j

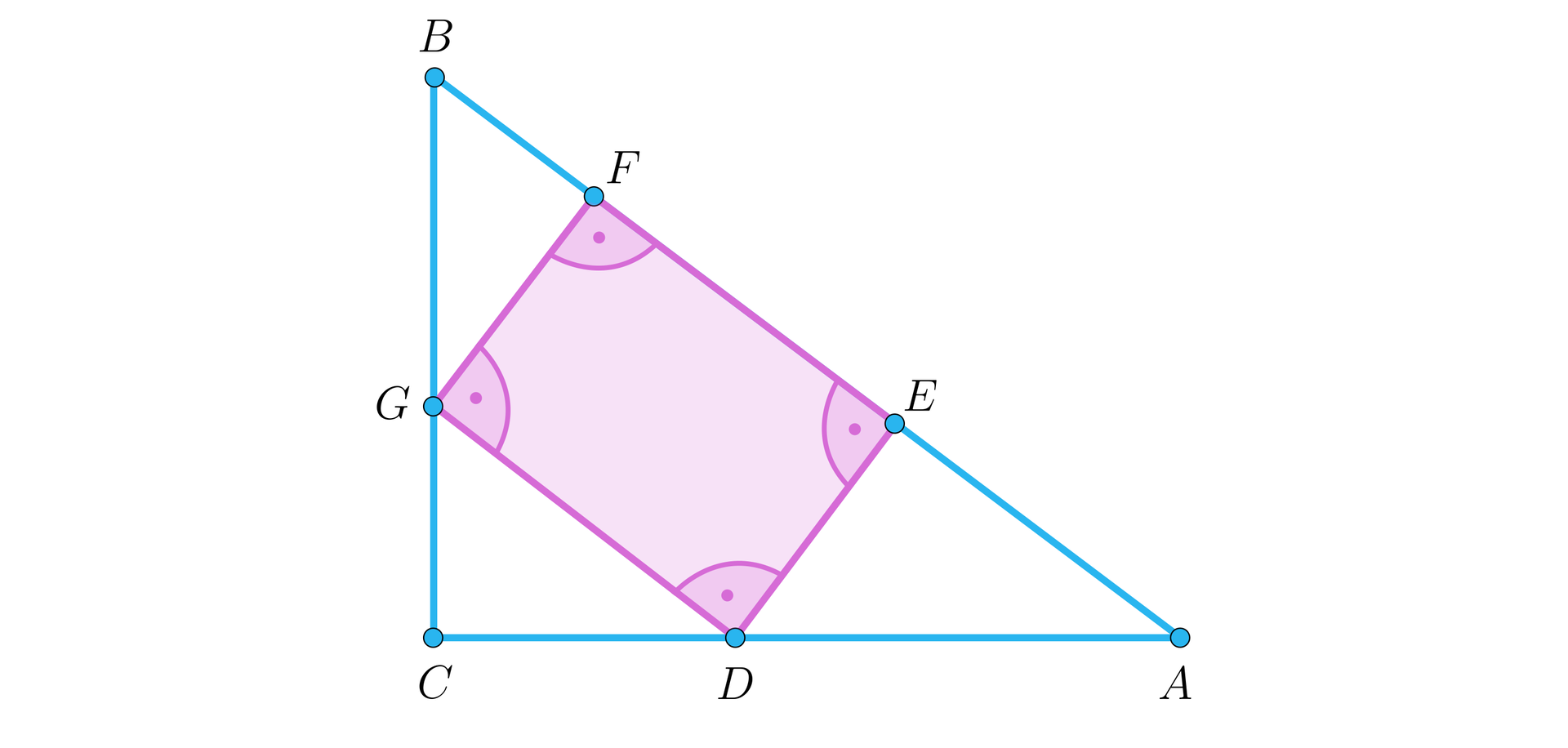
IlustracjaNa ilustracji przedstawiono trójkąt prostokątny ABC. Na przyprostokątnej AC zaznaczono punkt D. Na przyprostokątnej BC zaznaczono punkt G. Na przeciwprostokątnej AB zaznaczono punkt F oraz punkt E. Punkty zaznaczono w taki sposób, że po ich połączeniu powstał prostokąt, który zacieniowano.

Kwadrat wyznaczył trzy trójkąty prostokątne, z których dwa są przystające. Wyznacz pole trójkąta $A B C$ .

Mamy $|D E| = 4$ . Zauważmy, że tylko trójkąty $A D E$ oraz $B F G$ mogą być przystające. Oznaczmy $x = |A D| = |B G|$ . Wtedy $|B F| = \sqrt{x^{2} - 4^{2}} = |A E|$ . Ponieważ $|B F| + |E F| + |A E| = |A B|$ , więc $\sqrt{x^{2} - 4^{2}} + 4 + \sqrt{x^{2} - 4^{2}} = 12$ . Równanie, to możemy zapisać w postaci równoważnej $2 \sqrt{x^{2} - 4^{2}} = 8$ . Stąd $x^{2} - 16 = 16$ . Dodatnim rozwiązaniem ostatniego równania jest liczba $4 \sqrt{2}$ . Pozostaje zauważyć, że wówczas $|C G| = 2 \sqrt{2}$ , $|C D| = 2 \sqrt{2}$ . Zatem pole trójkąta $A B C$ jest równe $P_{A B C} = \frac{1}{2} \cdot 6 \sqrt{2} \cdot 6 \sqrt{2} = 36$ .

R1bfGbEaN6KBj21

Ćwiczenie 5

Łączenie par. Oceń prawdziwość podanych zdań. Wybierz PRAWDA, jeśli zdanie jest prawdziwe oraz FAŁSZ, jeśli zdanie nie jest prawdziwe.. Jeśli dwa boki w trójkącie prostokątnym

T_{1}

są odpowiednio równe dwóm bokom w trójkącie prostokątnym

T_{2}

, to

△ T_{1} \equiv △ T_{2}

.. Możliwe odpowiedzi: PRAWDA, FAŁSZ. Jeśli dwa kąty w trójkącie prostokątnym

T_{1}

są odpowiednio równe dwóm kątom w trójkącie prostokątnym

T_{2}

, to

△ T_{1} \equiv △ T_{2}

.. Możliwe odpowiedzi: PRAWDA, FAŁSZ. Jeśli dwa boki i jeden kąt w trójkącie prostokątnym

T_{1}

są odpowiednio równe dwóm bokom i kątowi w trójkącie prostokątnym

T_{2}

, to

△ T_{1} \equiv △ T_{2}

.. Możliwe odpowiedzi: PRAWDA, FAŁSZ. Jeśli dwa boki i dwa kąty w trójkącie prostokątnym są odpowiednio równe dwóm bokom i dwóm kątom w trójkącie prostokątnym , to .. Możliwe odpowiedzi: PRAWDA, FAŁSZ. E. Możliwe odpowiedzi: PRAWDA, FAŁSZ

Oceń prawdziwość podanych zdań. Wybierz PRAWDA, jeśli zdanie jest prawdziwe oraz FAŁSZ, jeśli zdanie nie jest prawdziwe.

	Prawda	Fałsz
Jeśli dwa boki w trójkącie prostokątnym $T_{1}$ są równe dwóm bokom w trójkącie prostokątnym $T_{2}$ , to $△ T_{1} \equiv △ T_{2}$ .	□	□
Jeśli dwa kąty w trójkącie prostokątnym $T_{1}$ są odpowiednio równe dwóm kątom w trójkącie prostokątnym $T_{2}$ , to $△ T_{1} \equiv △ T_{2}$ .	□	□
Jeśli dwa boki i jeden kąt w trójkącie prostokątnym $T_{1}$ są równe dwóm bokom i kątowi w trójkącie prostokątnym $T_{2}$ , to $△ T_{1} \equiv △ T_{2}$ .	□	□
Jeśli dwa boki i dwa kąty w trójkącie prostokątnym $T_{1}$ są odpowiednio równe dwóm bokom i dwóm kątom w trójkącie prostokątnym $T_{2}$ , to $△ T_{1} \equiv △ T_{2}$ .	□	□
Jeśli jedna z przyprostokątnych i jeden kąt ostry w trójkącie prostokątnym $T_{1}$ są odpowiednio równe przyprostokątnej i kątowi w trójkącie prostokątnym $T_{2}$ , to $△ T_{1} \equiv △ T_{2}$ .	□	□

RZMfHgn0V63U12

Ćwiczenie 6

Zaznacz poprawną odpowiedź. Przeciwprostokątna trójkąta prostokątnego $A B C$ ma długość $12$ , a jeden z kątów ostrych ma miarę $40 °$ . Trójkąt $D E F$ jest przystający do trójkąta $A B C$ , a jego kąty ostre mają miary $2 x + 3 y$ (większy kąt ostry) oraz $5 x - y$ . Wtedy:

$x = 5 °$ , $y = 10 °$
$x = 10 °$ , $y = 10 °$
$x = 15 °$ , $y = 25 °$
$x = 8 °$ , $y = 8 °$

RdIFb4pT8Ruxu3

Ćwiczenie 7

Udowodnij, że w trójkącie prostokątnym, w którym jeden z kątów ostrych jest dwa razy większy od drugiego kąta ostrego, przeciwprostokątna jest dwa razy dłuższa od jednej z przyprostokątnych.
Ułóż w kolejności etapy dowodu.

Zatem, w szczególności $"|"A E"|" = "|"B E"|"$ .
Zauważmy ponadto, że trójkąty $B E D$ oraz $B C D$ są trójkątami prostokątnymi o wspólnej przeciwprostokątnej $B D$ , w których $"|"∢ D B C"|" = "|"∢ D B E"|"$ . Zatem $△ B E D \equiv △ B C D$ , co oznacza w szczególności, że $"|"B E"|" = "|"B C"|"$ .
Poprowadźmy dwusieczną kąta $A B C$ i oznaczmy przez $D$ punkt, w którym ta dwusieczna przecina przyprostokątną $A C$ .
Stąd $"|"A B"|" = "|"A E"|" + "|"B E"|" = 2 \cdot "|"B E"|" = 2 \cdot "|"B C"|"$ . To kończy dowód.
Na mocy pierwszej cechy przystawania trójkątów prostokątnych, mamy, że $△ A E D \equiv △ B E D$ .
Otrzymaliśmy trójkąty $A E D$ oraz $B E D$ , które są trójkątami prostokątnymi o wspólnej przyprostokątnej $D E$ oraz równych przeciwprostokątnych $A D$ oraz $B D$ .
Rozważmy trójkąt prostokątny $A B C$ i przyjmijmy, że $"|"∢ A B C"|" = 2 \cdot "|"∢ C A B"|" < 90 °$ .
Poprowadźmy przez punkt $D$ prostą prostopadłą do przeciwprostokątnej, a punkt wspólny tej prostopadłej i przeciwprostokątnej oznaczmy jako $E$ .
Zauważmy, że trójkąt $A D B$ jest trójkątem równoramiennym, w którym $"|"A D"|" = "|"B D"|"$ .

Ćwiczenie 8

RkzkDeSdH3CAS

RF8QKx0Mjlptu

Aplet

Dla nauczyciela