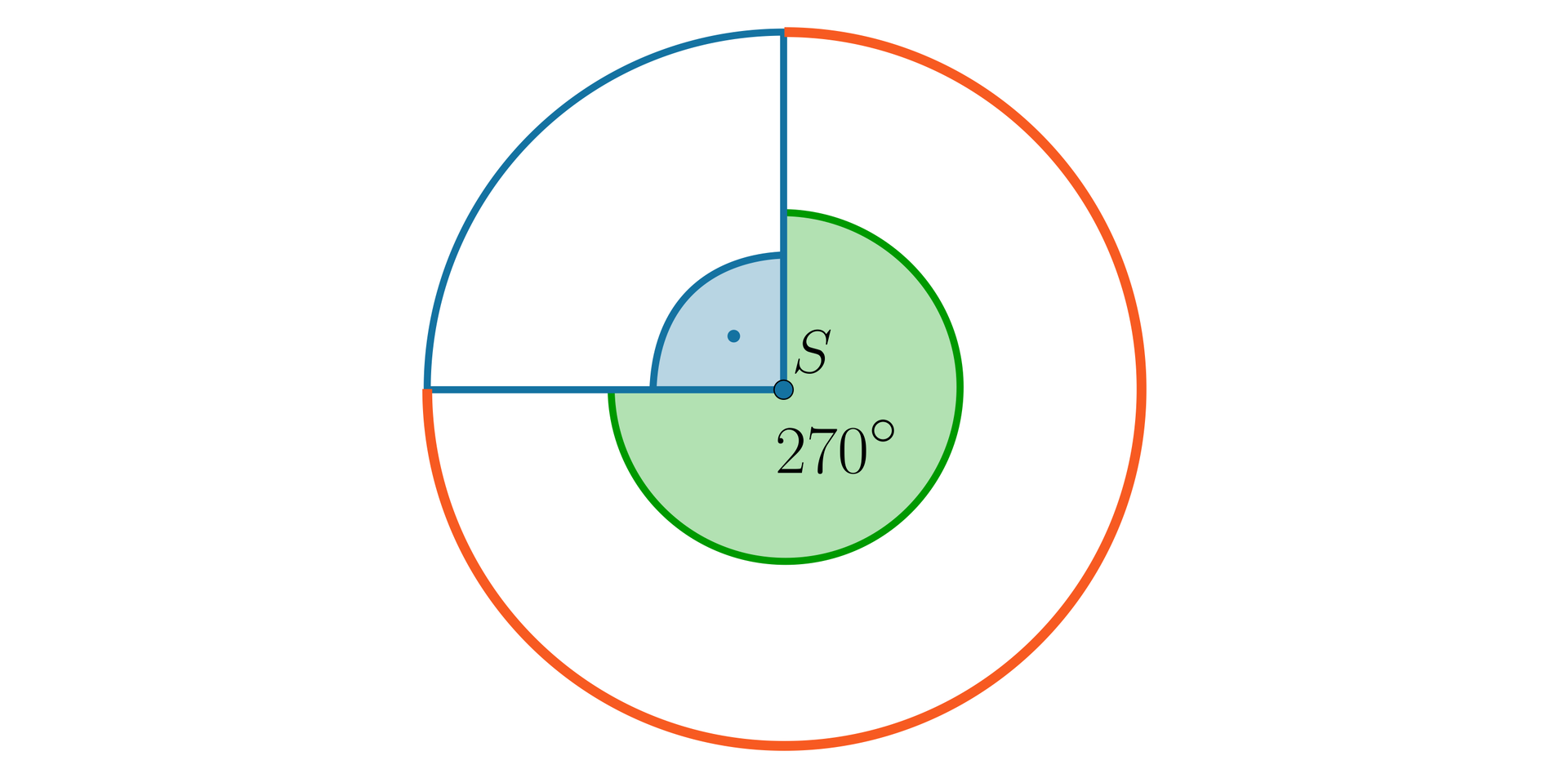
Wycinek koła. Odcinek koła
W tym materiale zawarte są informacje na temat wycinka i odcinka koła. Poznasz definicje, podstawowe pojęcia z nimi związane oraz zależności zachodzące pomiędzy wycinkiem i odcinkiem koła.
Wycinek koła

Film dostępny pod adresem /preview/resource/RN0ZFtSJaGW1i
Animacja przedstawia które figury możemy nazywać wycinkami koła.
Wycinkiem koła (wycinkiem kołowym) nazywamy część tego koła ograniczoną łukiem i ramionami kąta środkowego.

Kąt środkowy wyznacza w kole dwa wycinki kołowe.
W kole o promieniu wyznaczony jest wycinek koła przez kąt środkowy o mierze . Obliczymy pole tego wycinka.
Kąt o mierze stanowi kąta pełnego. Pole wycinka koła wyznaczonego przez ten kąt jest taką samą częścią pola całego koła. Stanowi więc pola całego koła:
Pole wycinka koła jest równe .
Kąt środkowy w okręgu o promieniu ma miarę . Oblicz długość łuku wyznaczonego przez ten kąt.

Obliczamy, że kąt stanowi część kąta pełnego. Szukana długość łuku jest więc równa długości okręgu:
Długość łuku wyznaczonego przez wycinek koła jest równa .
Zauważmy, że wycinek koła stanowi taką samą cześć koła, jaką częścią kąta pełnego jest kąt środkowy wyznaczający ten wycinek. Podobnie długość łuku wyznaczonego przez ten wycinek jest taką samą częścią długości okręgu, jaką częścią kąta pełnego jest kąt środkowy wyznaczający ten wycinek.
Pole wycinka koła wyznaczonego w kole o promieniu przez kąt środkowy o mierze jest równe
Długość łuku , wyznaczonego na okręgu o promieniu przez kąt środkowy o mierze , jest równa
Kąt środkowy w kole o promieniu ma miarę . Oblicz długość łuku wyznaczonego przez ten kąt. Wynik zaokrąglij do części dziesiątych.
Korzystamy ze wzoru na długość łuku wyznaczonego przez wycinek koła. Do wzoru podstawiamy:
Długość łuku wyznaczonego przez ten wycinek wynosi około .
W kole o promieniu kąt środkowy ma miarę . Oblicz pole wycinka koła wyznaczonego przez ten kąt.
Korzystamy ze wzoru na pole wycinka koła. Do wzoru podstawiamy i :
Pole wycinka koła jest równe około .
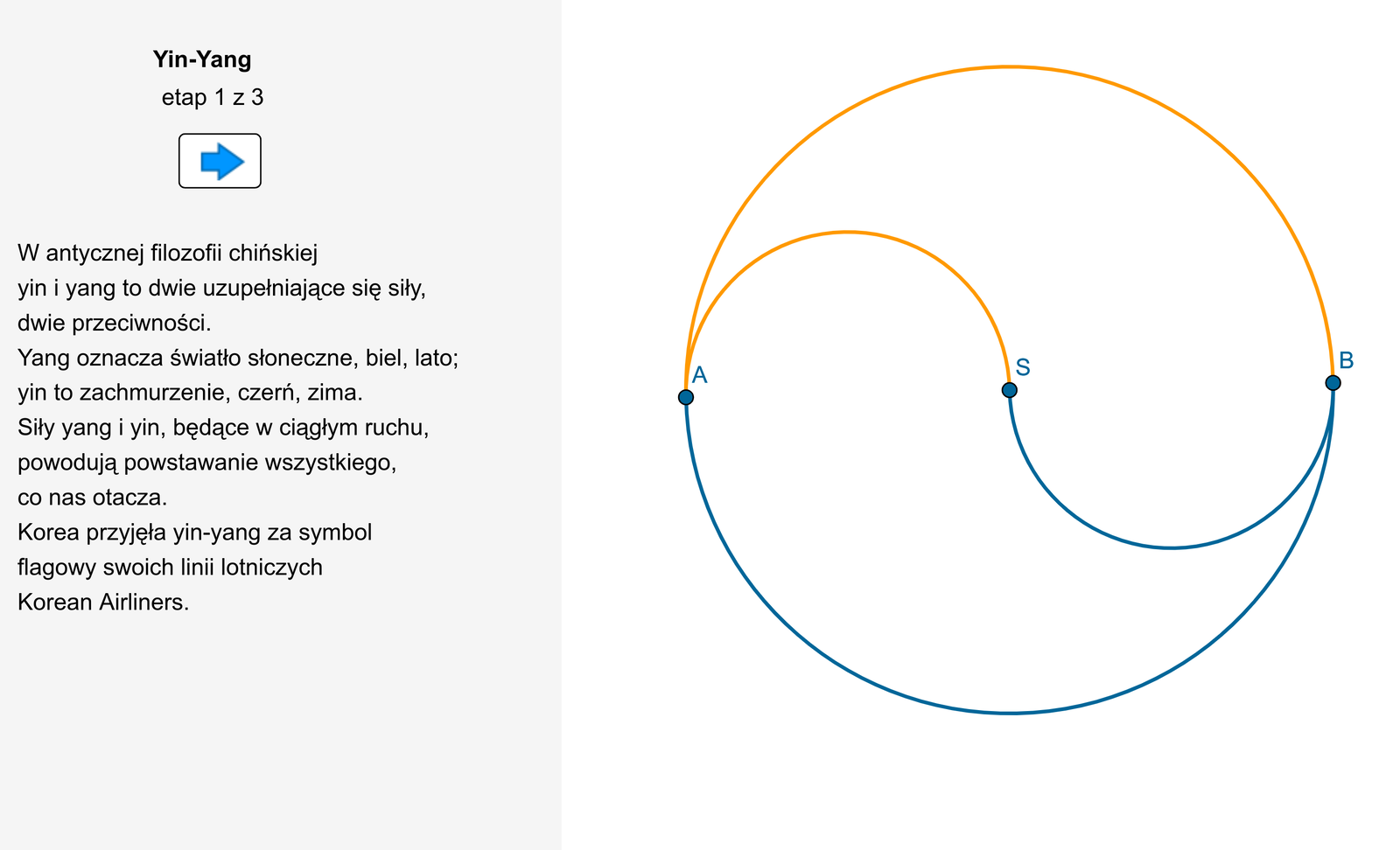
Podziel koło na równe części, przypominające Yin – Yang.
Wykaż, że w każdym przypadku otrzymane części mają równe pola.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PRFndazsT
W aplecie zamieszczono rysunek okręgu, na którym zaznaczono trzy punkty A, B oraz S. S jest środkiem koła. Na równej wysokości z punktem S na okręgu po lewej stronie zaznaczono punkt A i naprzeciwko zaznaczono punkt B. Punkt A i S połączone są łukiem, który jest górną połową okręgu o promieniu równym połowie długości między tymi punktami. Punkty S i B połączone są łukiem, który stanowi dolną połowę okręgu o promieniu równym długości połowie odległości pomiędzy punktem S i B. Po lewej stronie znajduje się komentarz do apletu o treści: W antycznej filozofii chińskiej, yin i yang to dwie uzupełniające się siły, dwie przeciwności. Yang oznacza światło słoneczne, biel, lato; Yin to zachmurzenie, czerń, zima. Siły yang i yin, będące w ciągłym ruchu, powodują powstawanie wszystkiego, co nas otacza. Korea przyjęła yin‑yang za symbol flagowy swoich linii lotniczych Korean Airliners.W drugim etapie apletu animowany jest opisany rysunek yin‑yang z zaznaczonym środkiem S. Górna część symbolu jest obracana w kierunku przeciwnym do wskazówek zegara do momentu aż pokryje się z dolną częścią symbolu. Komentarz do tego etapu: Widać, że obie figury Yin yang są przystające. Wystarczy jedną z nich obrócić wokół środka koła o 180 stopni lub przekształcić w symetrii środkowej względem środka koła. Animacje pozwalają uruchomić i zatrzymać dwa przyciski play oraz pauzy. W ostatnim etapie apletu przedstawiona jest pusta przestrzeń. Na początku widnieje komentarz z treścią : Ying Yang można przedstawić również jako podział koła odpowiednimi łukami na skończoną ilość figur o równych polach. Można udowodnić, że ich pola są równe.Pod komentarzem mamy suwak który oznaczony jest on literą n. Suwak można ustawiać od zera do dziesięciu i jego wartości zmieniają się co jeden. Na początku suwak ustawiony jest na zero. Każde przesunięcie powoduje powstanie opisanego w komentarzu podziału. Na przykład dla n równego 4 rysunek okręgu podzielono na cztery równych części, przypominające yang i yin. Z wcześniej oznaczonego punktu A poprowadzono niewielkie półkole wybrzuszone do góry. Z końca półkola poprowadzono wybrzuszony do dołu łuk biegnący do wcześniej oznaczonego punktu B. Z punktu A poprowadzono jeszcze cztery takie półkola o coraz większym promieniu, a z ich końców poprowadzono coraz krótsze łuki do punktu B. W ten sposób dokonano podziału okręgu na cztery równe części.
Odcinek koła

Film dostępny pod adresem /preview/resource/Rf5tTdUai8qS1
Animacja przedstawia które figury możemy nazywać odcinkami koła.
Odcinkiem koła (odcinkiem kołowym) nazywamy część koła odciętą przez cięciwę wraz z tą cięciwą.

Każda cięciwa wyznacza dwa odcinki koła. Średnica dzieli koło na dwa półkola.
Cięciwa ograniczająca odcinek koła wyznacza kąt środkowy . Ramiona tego kąta ograniczają łuk okręgu.

Pole odcinka koła jest różnicą pola wycinka koła wyznaczonego przez kąt i pola trójkąta, którego bokami są promienie okręgu i cięciwa.
Odcinek koła wyznaczony jest przez kąt środkowy o mierze i cięciwę długości . Oblicz pole odcinka.

Przyjmijmy oznaczenia takie, jak na rysunku. Wtedy trójkąt jest trójkątem prostokątnym, w którym kąt ma miarę (jako połowa kąta ).
Naprzeciw kąta o mierze leży przyprostokątna długości (jako połowa cięciwy). Korzystając z własności trójkąta prostokątnego o kątach , , , stwierdzamy, że i .
Obliczamy pole wycinka koła o promieniu wyznaczonego przez kąt środkowy o mierze
Obliczamy pole trójkąta
Pole odcinka koła jest równe różnicy pola wycinka i pola trójkąta .
Pole odcinka koła jest równe .
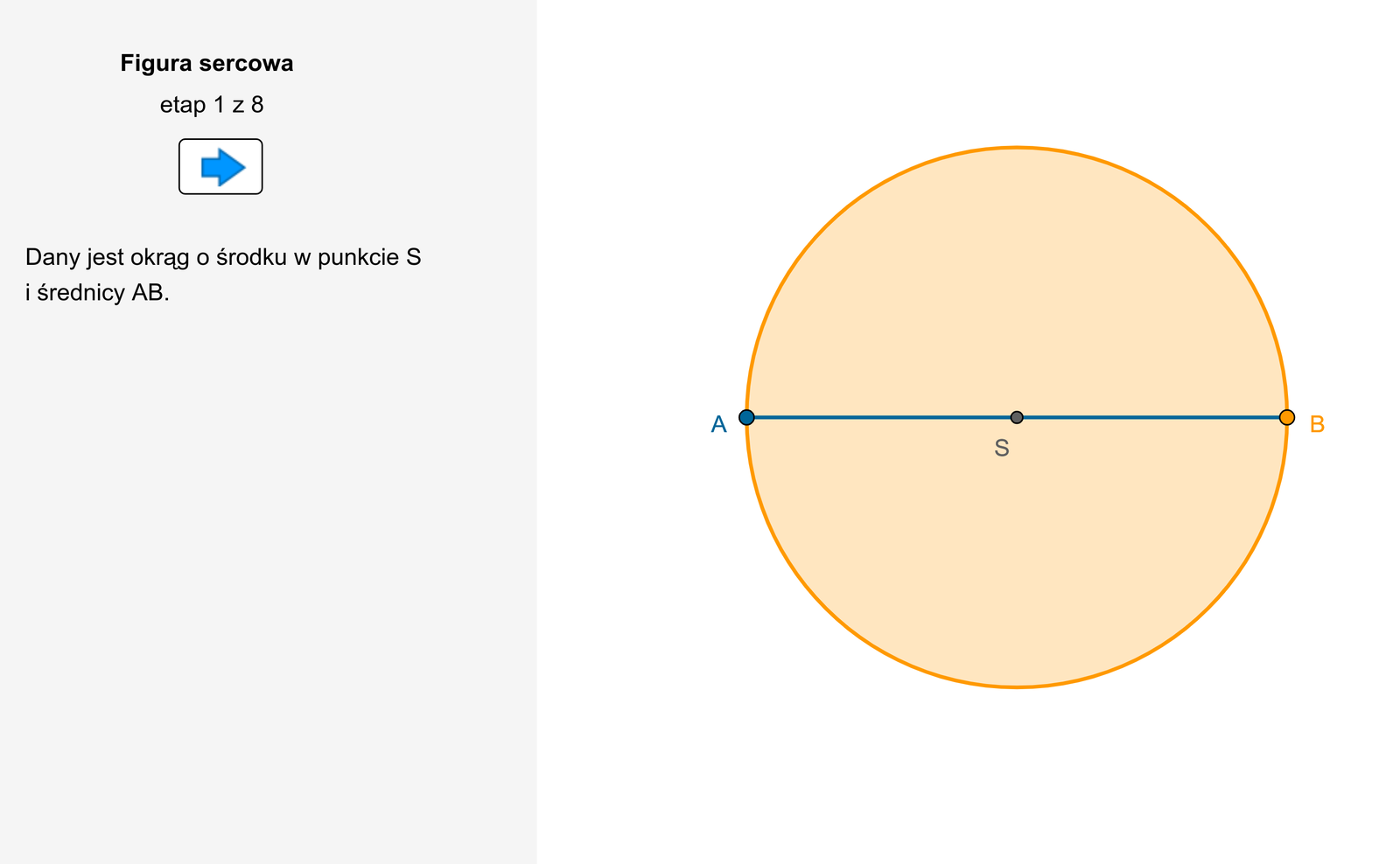
Nazwijmy niebieską figurę na rysunku „figurą sercową”.
Zastanów się, w jaki sposób powstała ta figura.
Sprawdź, że pole figury sercowej jest równe .
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PRFndazsT
W aplecie przedstawiono rysunek okręgu, na którym zaznaczono środek S oraz poziomą średnicę AB. Następnie poprowadzono prostopadłą średnicę do średnicy AB, której górny kraniec jest oznaczony literą C. W trzecim etapie apletu połączone zostały punkty A B C tworząc trójkąt o podstawie równej średnicy A B oraz wysokości S C, która jest promieniem rozważanego okręgu. Na podstawie znanego twierdzenia wiadomo, że trójkąt A B C jest prostokątny. Na przyprostokątnych trójkąta A B C które traktowane są jako średnice, zbudowane zostały dwa przystające okręgi o środkach w punktach O 1 i O2. W kolejnym kroku został zakreślony łuk A E B o promieniu C A i środku w punkcie C, który zawiera się w kole o średnicy AB. Punkt E leży na prostopadłej średnicy do średnicy AB pod środkiem okręgu S. Obszar zawarty między tym łukiem a łukiem A K C i B L C, gdzie K jest punktem leżącym na okręgu o środku O1 oraz L jest punktem leżący na okręgu o środku w punkcie O 2 ma kształt przypominający serce. W przedostatnim etapie animacji tabletu pokazuje się możliwość odczytania miary pól figur. Po zaznaczeniu tej możliwości dowiadujemy się, że pole figury sercowej jest równe 542,06 oraz pole koła o promieniu SA również równy jest 542, 06. W ostatnim etapie pojawia się możliwość zmiany położenia punktu B leżącego na okręgu o promieniu SA. Wówczas pole figury sercowej i pole koła o promieniu SA zmniejsza się lub powiększa odpowiednio z powiększającym lub zmniejszającym się promieniem. Bez względu na wielkość promienia obydwie miary pola są takie same.
Długość boku kwadratu jest równa .
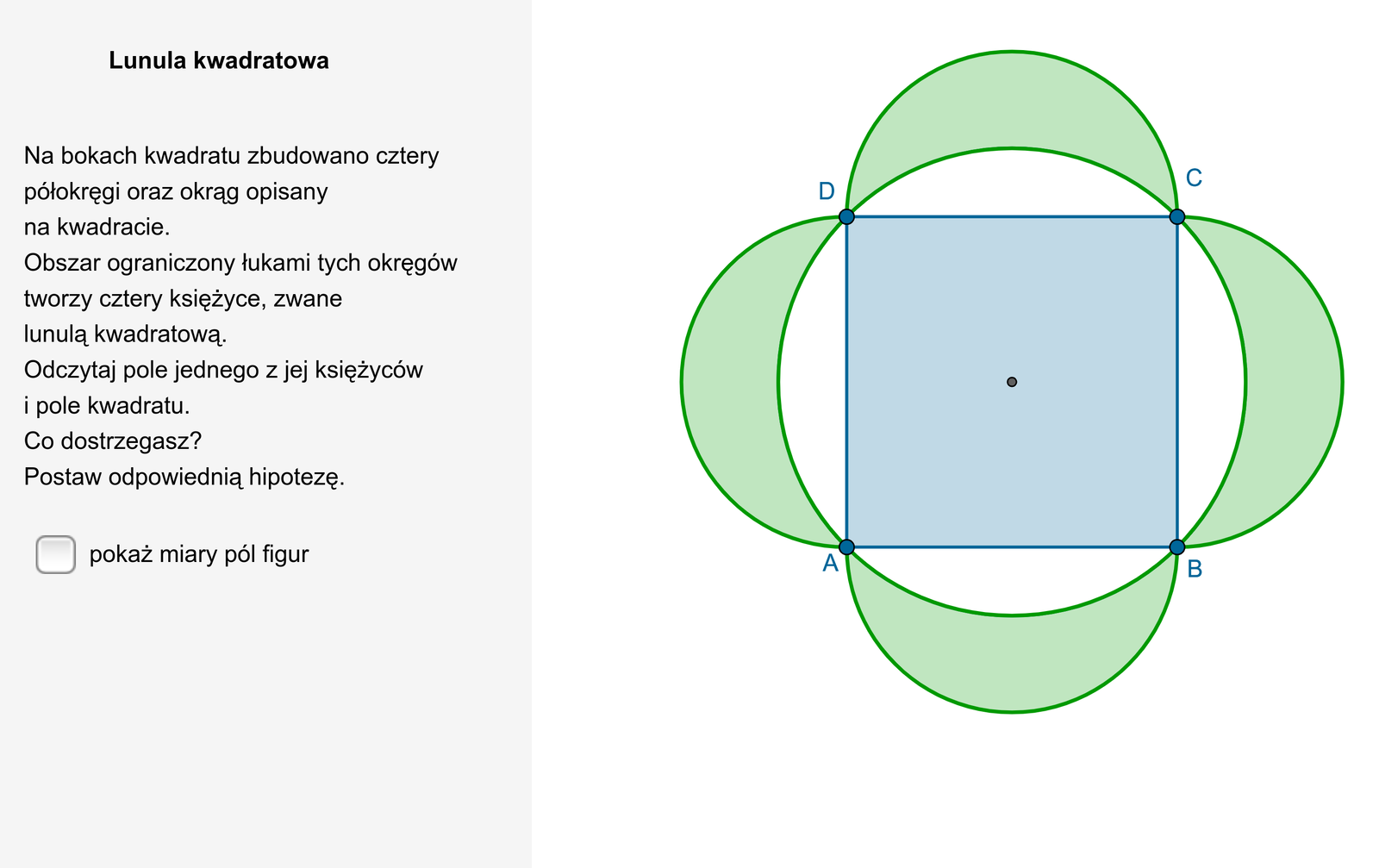
Na bokach kwadratu rysujemy księżyce Hipokratesa. Zapoznaj się z poniższym apletem przedstawiającym wspomniane księżyce.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PRFndazsT
Figurę utworzoną z tych księżyców nazwiemy lunulą (Luna po łacinie to Księżyc).
Oblicz pole jednej z części lunuli oraz pole lunuli, jeżeli bok kwadratu jest równy .
Porównaj to pole z polem kwadratu. Co zauważasz?
Na kwadracie o boku opisano okrąg. Na środku boku kwadratu zaznaczono punkt . Następnie narysowano okrąg o środku w punkcie o promieniu długości . Wówczas powstała figura składająca się z dwóch łuków okręgu przypomina księżyc, zwana lunulą. Oblicz jej pole.
Lunula trójkątna powstaje na bazie trójkąta prostokątnego równoramiennego.
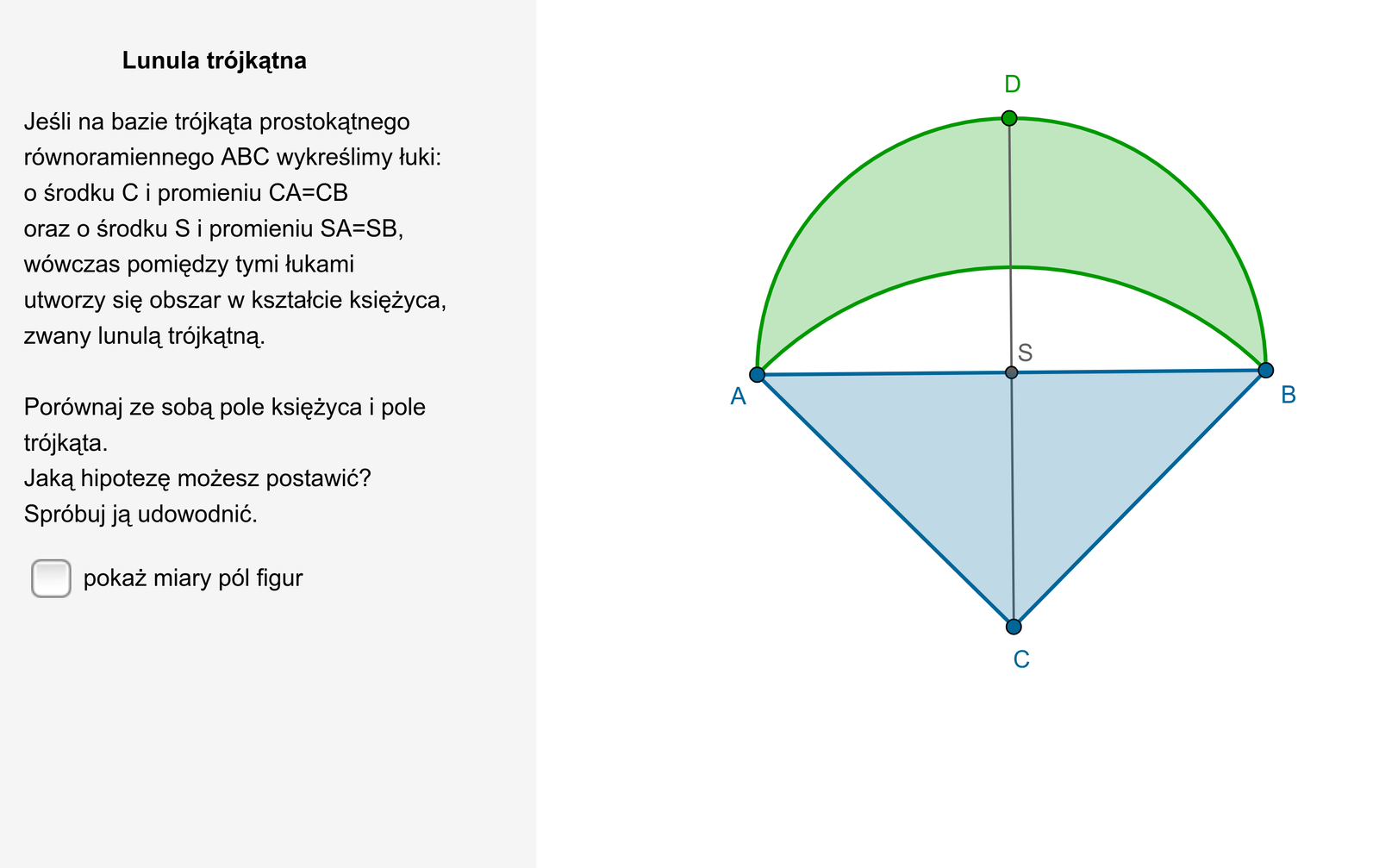
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PRFndazsT
Przyjrzyj się, jak powstaje lunula trójkątna i wykonaj podobną konstrukcję.
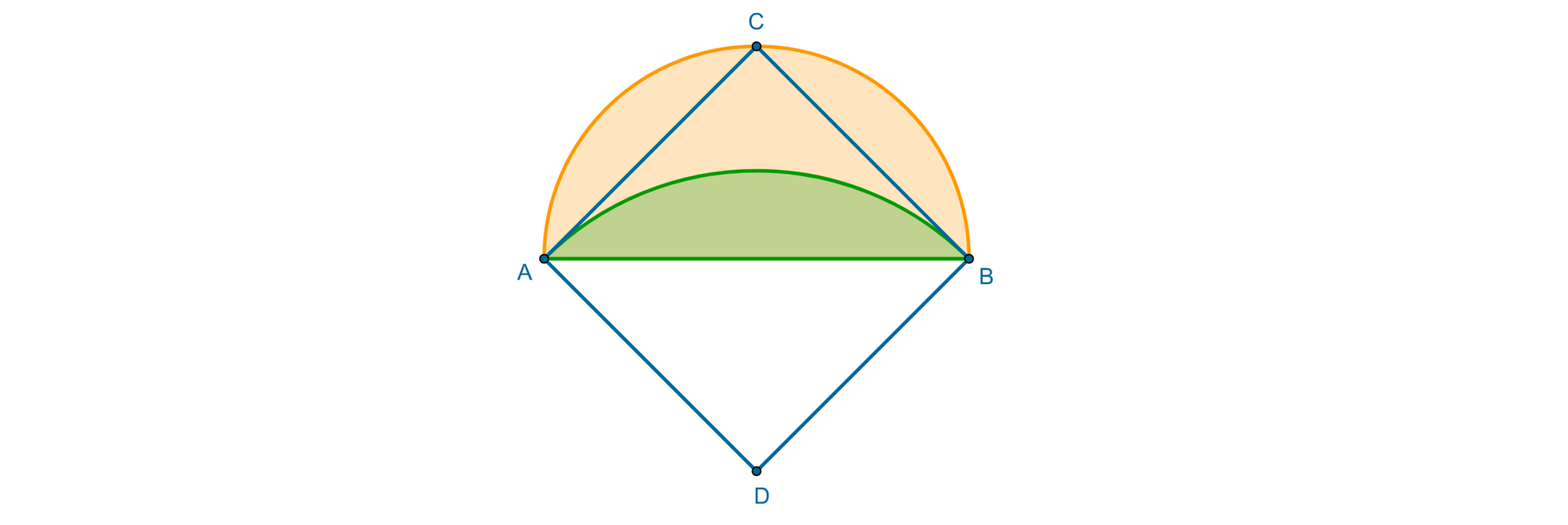
Oblicz pole połowy kwadratu (czyli pole trójkąta prostokątnego równoramiennego).
Oblicz pole lunuli.
Porównaj te pola. Co zauważasz?
Na trójkącie prostokątnym równoramiennym o dłucgościach boków , , opisano okrąg. Następnie na przeciwprostokątnej zaznaczono punkt , który dzieli ją na dwie równe części. Następnie narysowano okrąg o środku w punkcie o długości . W ten sposób powstała lunula trójkątna. Oblicz jej pole.
Koło o środku w punkcie i promieniu równym podzielono na jednakowe części. Następnie zamalowano na zielono niektóre z części – jak na rysunku. Oblicz pole zaznaczonych na zielono części tego koła, a następnie dopasuj prawidłowe wyniki.

b) Pole zaznaczonej na zielono części drugiej figury wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. .
c) Pole zaznaczonej na zielono części trzeciej figury wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. .
d) Pole zaznaczonej na zielono części czwartej figury wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. .
Koło o środku w punkcie ma promień równy . Oblicz pole pomalowanego na zielono wycinka tego koła.

b) Pole pomalowanego na zielono wycinka drugiej figury wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. .
c) Pole pomalowanego na zielono wycinka trzeciej figury wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. .
d) Pole pomalowanego na zielono wycinka czwartej figury wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. .
Kwiatek składa się z czterech jednakowych płatków i środka w kształcie koła. Płatek ma kształt wycinka koła wyznaczonego przez kąt środkowy o mierze w kole o promieniu . Środkowe koło ma promień równy . Oblicz pole powierzchni kwiatka. Wynik podaj z dokładnością do .

Które z linii mają tę samą długość? Zaznacz prawidłową odpowiedź.

- i
- i
- i
- i
Oblicz długość łuku w okręgu o promieniu , wyznaczonego przez kąt środkowy .

W kole o środku w punkcie i promieniu poprowadzono cięciwy i . Cięciwa ma długość .
Oblicz sumę pól odcinków koła wyznaczonych przez te cięciwy. Wynik podaj z dokładnością do dwóch miejsc po przecinku.

- Średnica tego koła jest równa .
- Długość okręgu ograniczającego to koło jest równa .
- Pole koła jest równe .
- Pole tego wycinka jest równe
Wykaż, że pole zaznaczonej na zielono lunuli jest równe polu trójkąta .

Narysuj koło o promieniu . Zamaluj część tego koła o polu .
Dane jest koło o promieniu . Oblicz na jakim kącie środkowym należy wyznaczyć wycinek tego koła, aby jego pole wynosiło .
Oblicz pole odcinka kołowego wyznaczonego w kole o promieniu przez cięciwę łączącą końce dwóch prostopadłych do siebie promieni.
Narysuj dowolny okrąg. Na okręgu zamaluj łuk stanowiący:
długości okręgu,
długości okręgu,
długości okręgu.
Dany jest pewien okrąg. Określ jaka musi być miara kąta środkowego , aby łuk wyznaczony przez ten kąt miał długość:
długości okręgu,
długości okręgu,
długości okręgu.
Kąt środkowy wyznacza w kole 1. jednakowe, 2. trzy, 3. dwa, 4. cztery, 5. różne wycinki kołowe.
Udowodnij, że średnica dzieli koło na dwa przystające odcinki kołowe.
W kole zaznaczono dwa wycinki kołowe o równych polach. Wykaż, że wycinki te wyznaczone są przez kąty środkowe o jednakowych miarach.