Wykres funkcji kwadratowej zapisanej wzorem w postaci kanonicznej. Wykres funkcji kwadratowej zapisanej wzorem w postaci ogólnej
Materiał ten poświęcony jest wykresom funkcji kwadratowych zapisanych wzorami w postaci kanonicznej i w postaci ogólnej. Analizując zawarte tu przykłady, dowiesz się jak w prosty sposób narysować wykres funkcji kwadratowej zapisanej wzorem w postaci kanonicznej oraz jak przekształcać wzory funkcji kwadratowych między obiema postaciami.
Wykres funkcji kwadratowej zapisanej wzorem w postaci kanonicznej
Rozpatrzmy parabolę o równaniu , gdzie jest ustaloną liczbą różną od zera.
Po przesunięciu tej paraboli o jednostek wzdłuż osi (w prawo, gdy lub w lewo, gdy ) oraz o jednostek wzdłuż osi (w górę, gdy
Aby uprościć zapisy, będziemy mówić, że na przykład „przesuwamy wykres o
Wykresem funkcji
Wykres funkcji
Osią symetrii wykresu funkcji
Maksymalny przedział, w którym funkcja
Zbiorem wartości funkcji
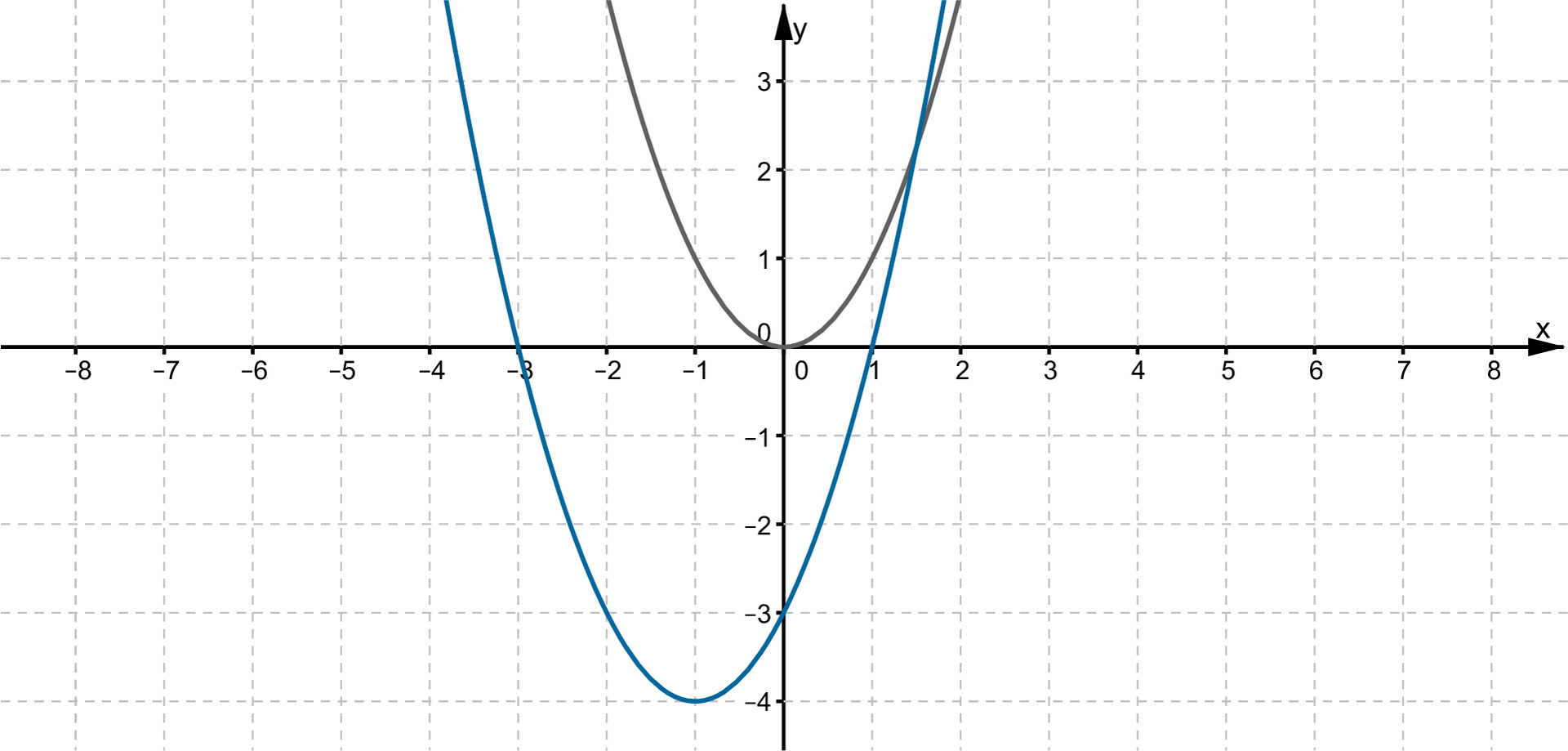
Wykresem funkcji
Wykres funkcji
Osią symetrii wykresu funkcji
Maksymalny przedział, w którym funkcja
Zbiorem wartości funkcji

Wykresem funkcji
Wykres funkcji
Osią symetrii wykresu funkcji
Maksymalny przedział, w którym funkcja
Zbiorem wartości funkcji

Wykresem funkcji
Wykres funkcji
Osią symetrii wykresu funkcji
Maksymalny przedział, w którym funkcja
Zbiorem wartości funkcji

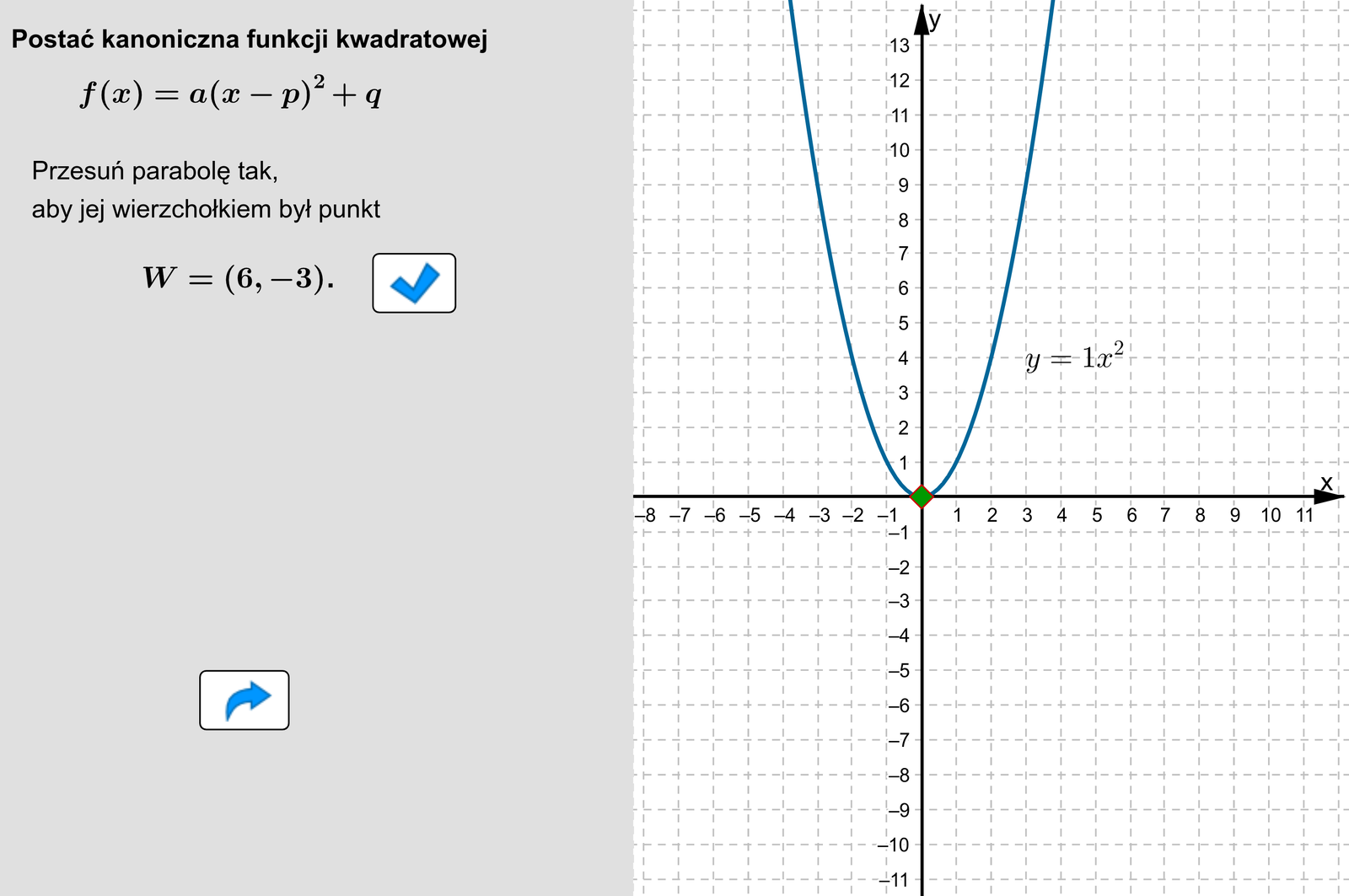
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/Pr22VCRSd
Postać kanonicza funkcji kwadratowej, to
Na przykład jeżeli przesuniemy parabolę określoną wzorem
Wykres każdej z omawianych funkcji rysowaliśmy, korzystając z pomysłu przedstawionego na początku tej lekcji. Przepis ten da się zastosować do wykresu każdej funkcji kwadratowej, której wzór umiemy zapisać w postaci
Zauważmy, że w przypadku funkcji
oraz
natomiast w przypadku funkcji
a także
Zatem każdą z funkcji
Wzór
Wykres funkcji kwadratowej zapisanej wzorem w postaci ogólnej
Na jednym rysunku naszkicujemy wykresy funkcji
Przekształcimy wzór funkcji
Wobec tego funkcje
Wykresem obu tych funkcji jest parabola, która powstaje w wyniku przesunięcia paraboli o równaniu
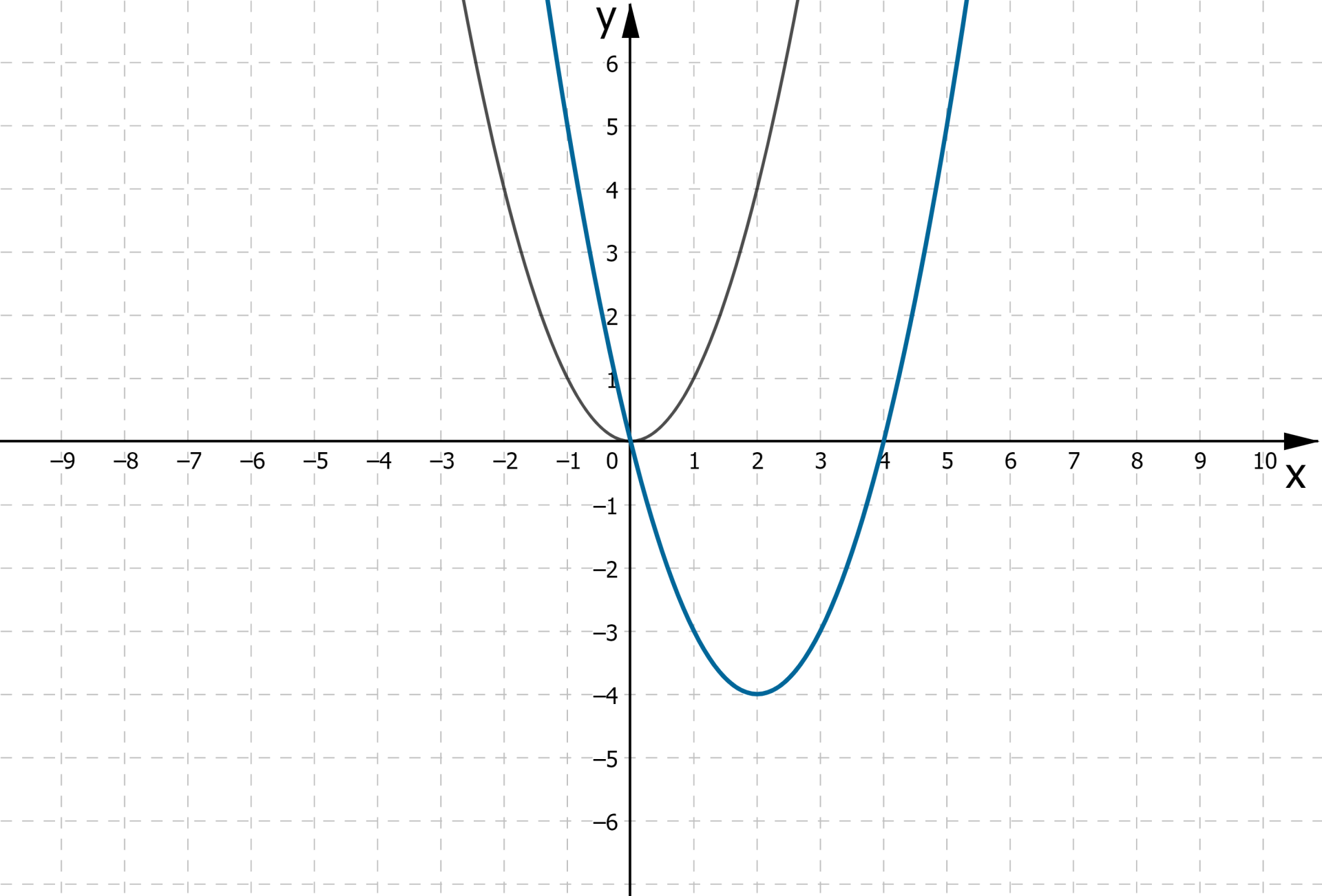
Wykażemy, że przesuwając równolegle parabolę
Po przesunięciu paraboli

Narysujemy wykres funkcji
Wykorzystamy w tym celu pomysł z poprzedniego przykładu. Spodziewamy się, że wykres funkcji
Jeżeli przyjmiemy
Wystarczy zatem przyjąć
Wobec tego wykresem funkcji

Narysujemy wykres funkcji
Zauważmy, że wzór funkcji
Wzór funkcji
Wynika z tego, że wykresem funkcji

Narysujemy wykres funkcji
Zauważmy, że wzór funkcji
Ponadto dla każdej liczby
Wzór funkcji
Wynika z tego, że wykresem funkcji

Na rysunkach przedstawiono wykresy kilku różnych funkcji. Zapiszemy wzór każdej z tych funkcji w postaci kanonicznej oraz w postaci ogólnej.
Wykres funkcji kwadratowej
f R1FUJq18BvEwI1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Wierzchołkiem paraboli jest punkt
1 , - 1 y = a x - 1 2 - 1 0 , 0 a ⋅ 0 - 1 2 - 1 = 0 a = 1 f f x = x - 1 2 - 1 f x = x 2 - 2 x + 1 - 1 f x = x 2 - 2 x Wykres funkcji kwadratowej
g RncsAWGuGZlQo1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Wierzchołkiem paraboli jest punkt
- 2 , 2 y = a x + 2 2 + 2 0 , 0 a ⋅ 0 + 2 2 + 2 = 0 a = - 1 2 g g x = - 1 2 x + 2 2 + 2 g x = - 1 2 x 2 + 4 x + 4 + 2 g x = - 1 2 x 2 - 2 x Wykres funkcji kwadratowej
h RXKpPm6PfpqB81 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Wierzchołkiem paraboli jest punkt
3 , 4 y = a x - 3 2 + 4 1 , 0 a ⋅ 1 - 3 2 + 4 = 0 a = - 1 h h x = - x - 3 2 + 4 h x = - x 2 - 6 x + 9 + 4 h x = - x 2 + 6 x - 5 Wykres funkcji kwadratowej
k Rzgg8DDRPTA5y1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Wierzchołkiem paraboli jest punkt
1 , 1 y = a x - 1 2 + 1 0 , 3 a ⋅ 0 - 1 2 + 1 = 3 a = 2 k k x = 2 x - 1 2 + 1 k x = 2 x 2 - 2 x + 1 + 1 k x = 2 x 2 - 4 x + 3
-
przecina oś
Ox -
przecina oś
Oy -
ma dokładnie jeden punkt wspólny z prostą
y = 1 -
ma dwa punkty wspólne z prostą
y = 5
-
Najmniejsza wartość funkcji
f x = 3 x 2 + 1 3 -
Najmniejsza wartość funkcji
g x = ( x – 2 ) 2 – 3 – 3 -
Największa wartość funkcji
h x = – 2 x 2 + 3 3 -
Największa wartość funkcji
k x = – ( x + 1 ) 2 + 2 1
Jaki jest współczynnik
Oś symetrii paraboli to prosta określona równaniem
Oś symetrii paraboli to prosta określona równaniem
Oś symetrii paraboli to prosta określona równaniem
Oś symetrii paraboli to prosta określona równaniem
Ramiona paraboli skierowane są Tu uzupełnij.Wykresem funkcji
Ramiona paraboli skierowane są Tu uzupełnij.Wykresem funkcji
Ramiona paraboli skierowane są Tu uzupełnij.Wykresem funkcji
Ramiona paraboli skierowane są Tu uzupełnij.
Odpowiedź: Maksymalny przedział, w którym
Odpowiedź: Maksymalny przedział, w którym
Odpowiedź: Maksymalny przedział, w którym
Odpowiedź: Maksymalny przedział, w którym
Odpowiedź: Postać kanoniczna tej funkcji to
Odpowiedź: Postać kanoniczna tej funkcji to
Odpowiedź: Postać kanoniczna tej funkcji to
Odpowiedź: Postać kanoniczna tej funkcji to
Odpowiedź: Postać kanoniczna tej funkcji to
Odpowiedź: Postać kanoniczna tej funkcji to
Odpowiedź: Postać kanoniczna tej funkcji to
Odpowiedź: Postać kanoniczna tej funkcji to
Odpowiedź: Postać kanoniczna tej funkcji to
Odpowiedź: Postać kanoniczna tej funkcji to
Odpowiedź: Postać kanoniczna tej funkcji to
Odpowiedź: Postać kanoniczna tej funkcji to
Na rysunku jest przedstawiony wykres funkcji kwadratowej
Zapoznaj się z opisem rysunku, na którym przedstawiony jest wykres funkcji kwadratowej
RH6hDVkjM0MoC1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.RcfGl37AXzyGY1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.RTwLtHN9PSAG01 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.RHpoIyeeEhmuJ1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.















