Zadania powtórkowe przed egzaminem maturalnym cz.2
Materiał zawiera zadania powtórkowe przed egzaminem maturalnym. Spróbuj je rozwiązać samodzielnie. Jeśli napotkasz problemy, możesz skorzystać z podpowiedzi zamieszczonych poniżej.
Niech i . ,, dla ,, dla i ., 2. Potęgi Własności działań na potęgach:
Niech , , i będą liczbami rzeczywistymi. ,, dla ,,, dla ,., 3. Koło Obwód koła obliczamy ze wzoru: .Pole koła obliczamy ze wzoru: .Pole wycinka koła wyznaczonego przez kąt środkowy obliczamy ze wzoru: ., 4. Układ równań Jest: oznaczony - jeżeli ma jedno rozwiązanie,nieoznaczony - jeżeli ma nieskończenie wiele rozwiązań.sprzeczny - jeżeli nie ma rozwiązań., 5. Procenty Procent:
.
Obliczanie procentu z liczby :
., 6. Proporcje Proporcja to równość dwóch stosunków postaci .Podstawowa własność proporcji mówi, że iloczyn wyrazów i jest równy iloczynowi wyrazów i , czyli ., 7. Stożek Wzór na pole powierzchni całkowitej: . Wzór na objętość stożka: , gdzie oznacza promień koła w podstawie, a oznacza wysokość stożka., 8. Sześcian i czworościan foremny SześcianPole powierzchni całkowitej: ,Objętość: ,Przekątna:gdzie oznacza długość krawędzi sześcianu. Czworościan foremnyPole powierzchni całkowitej: .Objętość: . oznacza krawędź czworościanu., 9. Trójkąt prostokątny , i W trójkącie prostokątnym o podanych kątach, na przeciwko kąta mamy bok długości , na przeciwko kąta mamy bok długości , a przeciwprostokątna tego trójkąta ma długość ., 10. Odległość między punktami Odległość między punktami , możemy obliczyć ze wzoru: ., 11. Średnia arytmetyczna i mediana Średnia arytmetyczna:
Aby obliczyć średnią arytmetyczną zestawu danych, należy je do siebie dodać i otrzymaną sumę podzielić przez ich liczbę.Mediana:
Jeżeli w zestawie znajduje się nieparzysta liczba wyników, to medianą jest wyraz znajdujący się na środku uporządkowanego rosnąco zestawu.Jeżeli w zestawie jest parzysta liczba danych, to mediana jest równa średniej arytmetycznej dwóch środkowych wyrazów uporządkowanego rosnąco zestawu., 12. Twierdzenie Talesa Jeżeli dany jest kąt, którego ramiona są przecięte dwiema prostymi równoległymi, to odcinki powstałe w wyniku przecięcia tych prostych na jednym ramieniu kąta, mają długości proporcjonalne do długości odpowiednich odcinków z drugiego ramienia kąta.
Pierwiastki:
Własności działań na pierwiastkach:
Niech i
,
, dla ,
,
, dla i .
Potęgi:
Własności działań na potęgach:
Niech , , i będą liczbami rzeczywistymi.
,
, dla ,
,
, dla ,
.
Procenty:
Procent:
Obliczanie procentu z liczby: .
Stożek:
Wzór na pole powierzchni całkowitej: .
Wzór na objętość stożka: ,
gdzie oznacza promień koła w podstawie, a oznacza wysokość stożka.
Koło
Obwód koła obliczamy ze wzoru: .
Pole koła obliczamy ze wzoru: .
Pole wycinka koła wyznaczonego przez kąt środkowy obliczamy ze wzoru: .
Układ równań:
Jest:
oznaczony – jeżeli ma jedno rozwiązanie,
nieoznaczony – jeżeli ma nieskończenie wiele rozwiązań,
sprzeczny – jeżeli nie ma rozwiązań.
Sześcian i czworościan foremny:
Sześcian:
Pole powierzchni całkowitej: ,
Objętość: ,
Przekątna: ,
gdzie oznacza długość krawędzi sześcianu.
Czworościan foremny:
Pole powierzchni całkowitej: .
Objętość: .
oznacza krawędź czworościanu.
Proporcje
Proporcja to równość dwóch stosunków postaci .
Podstawowa własność proporcji mówi, że iloczyn wyrazów i jest równy iloczynowi wyrazów i , czyli .
Trójkąt prostokątny , i
W trójkącie prostokątnym o podanych kątach, na przeciwko kąta mamy bok długości , na przeciwko kąta mamy bok długości , a przeciwprostokątna tego trójkąta ma długość .
Odległość między punktami
Odległość między punktami , możemy obliczyć ze wzoru: .
Średnia arytmetyczna i mediana:
Średnia arytmetyczna:
Aby obliczyć średnią arytmetyczną zestawu danych, należy je do siebie dodać i otrzymaną sumę podzielić przez ich liczbę.
Mediana
Jeżeli w zestawie znajduje się nieparzysta liczba wyników, to medianą jest wyraz znajdujący się na środku uporządkowanego rosnąco zestawu.
Jeżeli w zestawie jest parzysta liczba danych, to mediana jest równa średniej arytmetycznej dwóch środkowych wyrazów uporządkowanego rosnąco zestawu.
Twierdzenie Talesa:
Jeżeli dany jest kąt, którego ramiona są przecięte dwiema prostymi równoległymi, to odcinki powstałe w wyniku przecięcia tych prostych na jednym ramieniu kąta, mają długości proporcjonalne do długości odpowiednich odcinków z drugiego ramienia kąta.
Zosia i Krzyś przeprowadzili ankietę wśród pewnej grupy mieszkańców swojego osiedla na temat: „Jakiego gatunku muzyki lubisz słuchać najbardziej?” Każdy mógł wybrać tylko jedną odpowiedź. Wyniki przedstawia diagram.

Zaznacz zdanie prawdziwe. Możliwe odpowiedzi: 1. Jeżeli z dwóch pierwszych pojemników odlano po wody, do trzeciego dolano wody, a do czwartego dolano wody, to średnia masa wody w pojemnikach nie zmieniła się., 2. Jeżeli do trzech pojemników dolano po wody, to średnia masa wody w pojemnikach wyniosła .
Na diagramie przedstawiono liczbę bramek zdobytych przez pewnego piłkarza w ciągu sezonu.
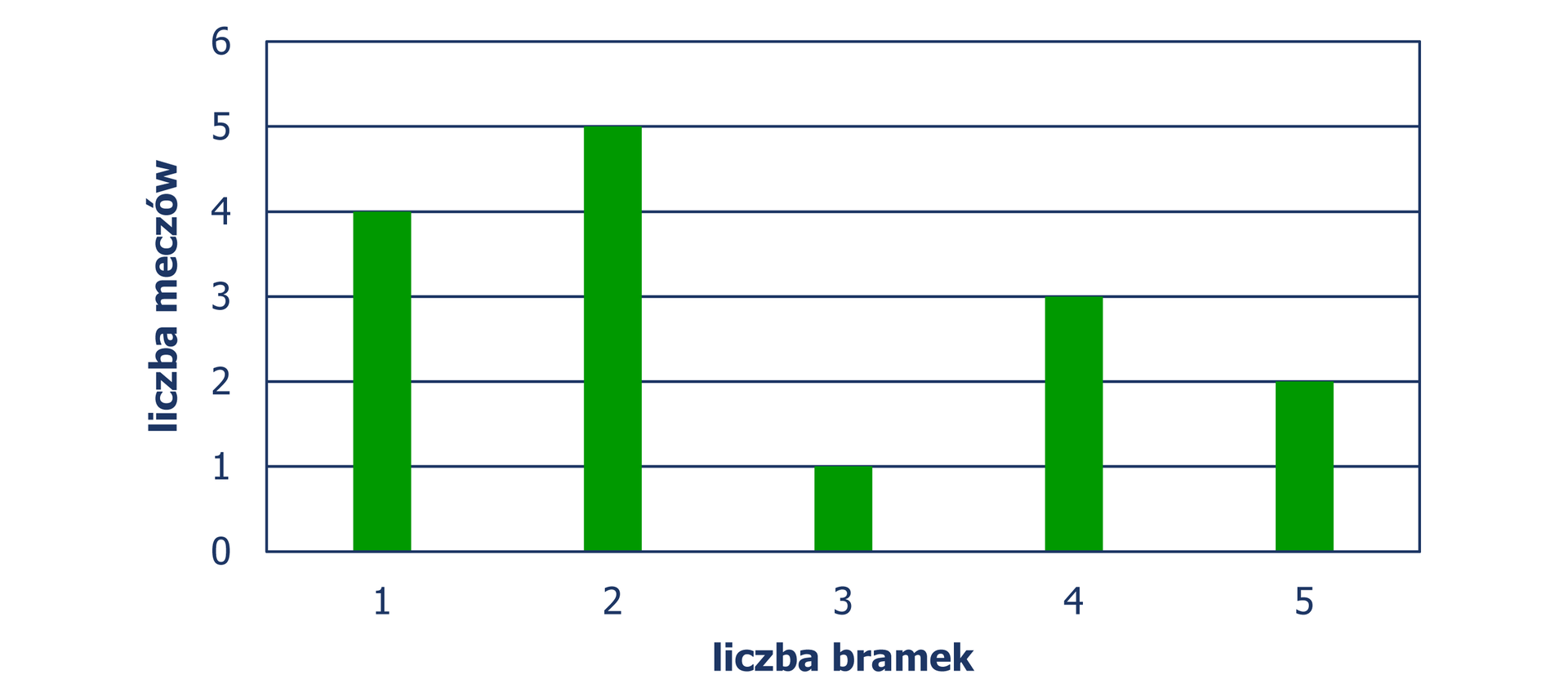
Z diagramu wynika, że Możliwe odpowiedzi: 1. średnia liczba zdobytych bramek w jednym meczu wynosi ., 2. najczęściej powtarzającą się liczbą zdobytych bramek jest ., 3. mediana liczby zdobytych bramek wynosi ., 4. liczba meczów w sezonie wyniosła .
- średnia liczba zdobytych bramek w jednym meczu wynosi
- najczęściej powtarzającą się liczbą zdobytych bramek jest
- mediana liczby zdobytych bramek wynosi
- liczba meczów w sezonie wyniosła
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Prawdopodobieństwo wylosowania przez trzecią osobę losu przegrywającego jest większe od ., 2. Trzecia osoba musiałaby kupić losów, aby mieć pewność, że przynajmniej jeden z nich będzie wygrywający., 3. Prawdopodobieństwo wylosowania losu wygrywającego przez trzecią osobę jest mniejsze niż ., 4. Pierwsze dwie osoby miały taką samą szansę na przegraną w tej loterii.
- Prawdopodobieństwo wylosowania przez trzecią osobę losu przegrywającego jest większe od .
- Trzecia osoba musiałaby kupić losów, aby mieć pewność, że przynajmniej jeden z nich będzie wygrywający.
Zaznacz zdanie prawdziwe. Możliwe odpowiedzi: 1. W hurtowni pozostało gruszek., 2. Pierwszego dnia sprzedano gruszek.
Trójkąty i są równoramienne.
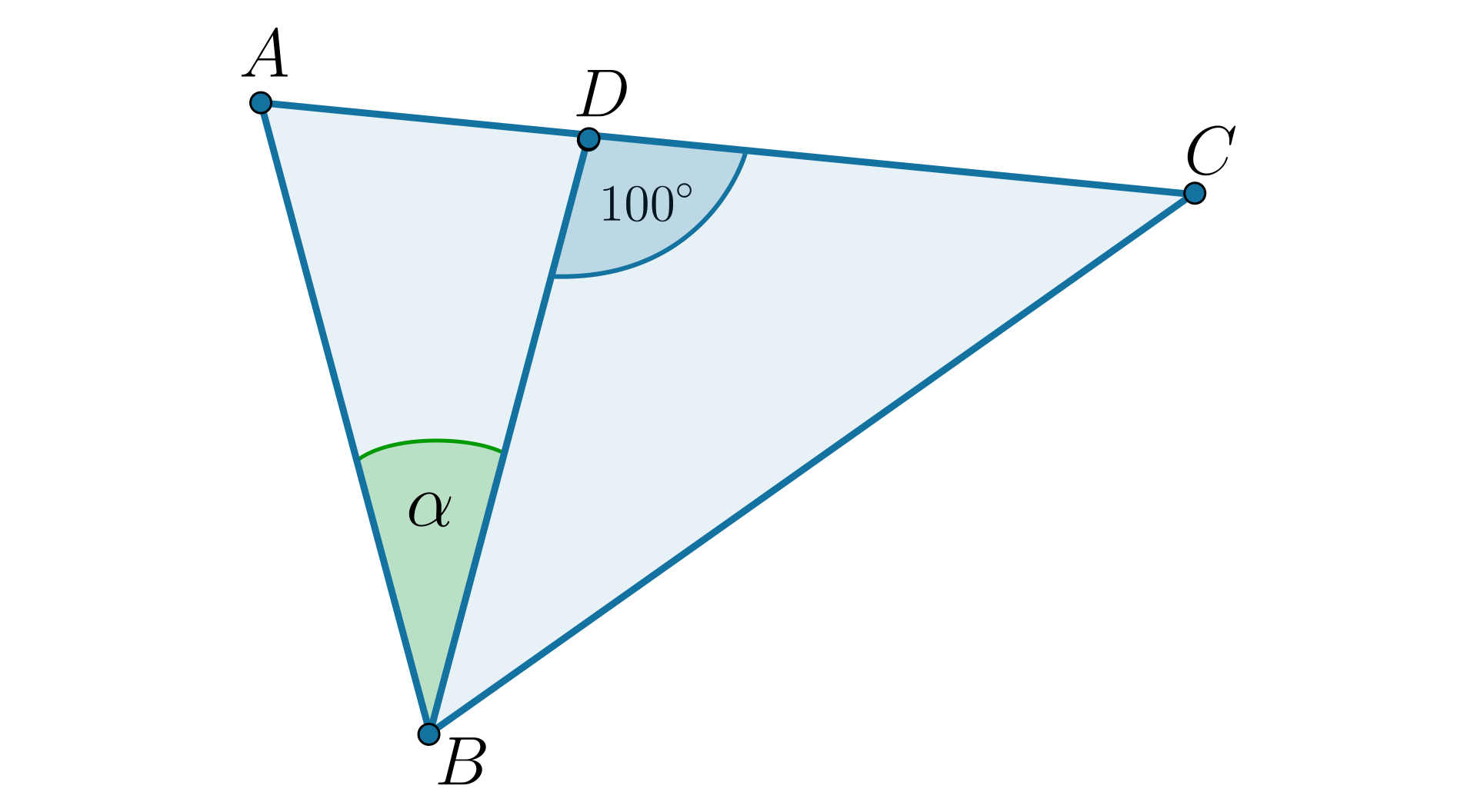
Ile wynosi różnica kąta przy podstawie trójkąta i kąta między ramionami trójkąta ? Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. ., 2. ., 3. ., 4. .
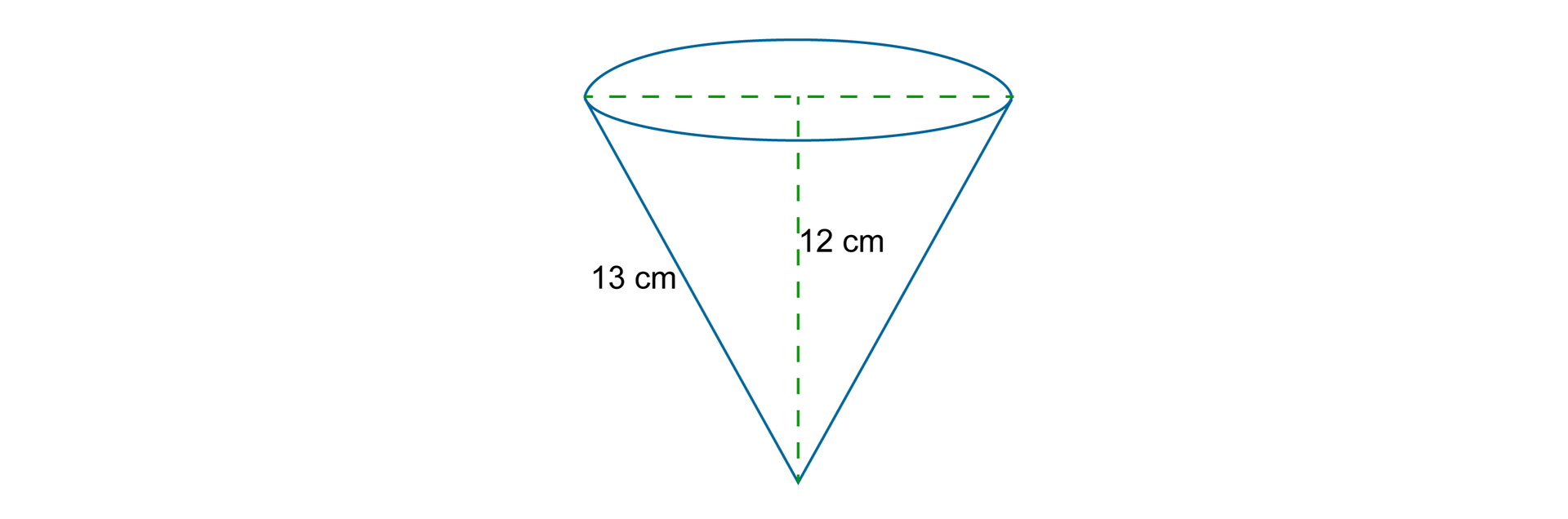
Wafel w kształcie stożka napełniony jest bitą śmietaną.
Uzasadnij, że jeśli od liczby trzycyfrowej odejmiemy sumę jej cyfr, to otrzymany wynik będzie liczbą podzielną przez .
Promień poniższego koła jest równy . Przyjmij i oblicz pole zacieniowanej figury.

Połączono odcinkami środki boków kwadratu . Otrzymano czworokąt . Uzasadnij, że pole czworokąta jest dwa razy mniejsze od pola kwadratu .