Zadania powtórkowe przed egzaminem maturalnym cz.4

Pokaż ćwiczenia:

Materiał zawiera zadania powtórkowe przed egzaminem maturalnym. Spróbuj je rozwiązać samodzielnie. Jeśli napotkasz problemy możesz skorzystać z podpowiedzi zamieszczonych poniżej.

Pierwiastki:

Własności działań na pierwiastkach:

Niech $a \geq 0$ i $b \geq 0$ .

$\sqrt{a} \cdot \sqrt{b} = \sqrt{a b}$ ,
$\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$ , dla $b \neq 0$ ,
$\sqrt{a^{2}} = |a|$ ,
$\sqrt[m]{a^{n}} = a^{\frac{n}{m}}$ , dla $m \geq 0$ i $n > 0$ .

Potęgi:

Własności działań na potęgach:

Niech $a$ , $b$ , $n$ i $m$ będą liczbami rzeczywistymi.

$a^{m} \cdot a^{n} = a^{m + n}$ ,
$a^{m} : a^{n} = a^{m - n}$ , dla $a \neq 0$ ,
${(a \cdot b)}^{m} = a^{m} \cdot b^{m}$ ,
${(a : b)}^{m} = a^{m} : b^{m}$ , dla $b \neq 0$ ,
${(a^{n})}^{m} = a^{m \cdot n}$ .

Walec i kula:

Walec:

Wzór na pole powierzchni całkowitej: $P_{c} = 2 π r (r + H)$ .

Wzór na objętość walca: $V = π r^{2} \cdot H$ ,

gdzie $r$ oznacza promień koła w podstawie, a $H$ oznacza wysokość walca.

Kula:

Wzór na pole powierzchni całkowitej kuli: $P_{c} = 4 π r^{2}$ ,

Objętość kuli: $V = \frac{4}{3} π r^{3}$ ,

gdzie $r$ oznacza promień kuli.

Trójkąty:

Trójkąt równoboczny: Wzór na pole: $P = \frac{a^{2} \sqrt{3}}{4}$ ,

gdzie $a$ oznacza długość boku trójkąta.

Wysokość w trójkącie równobocznym: $h = \frac{a \sqrt{3}}{2}$ .

Zależność pomiędzy wysokością a promieniem okręgu wpisanego lub opisanego na trójkącie równobocznym:

$r = \frac{1}{3} h$ ,
$R = \frac{2}{3} h$ ,

gdzie $r$ oznacza promień okręgu wpisanego w trójkąt, a $R$ promień okręgu opisanego na trójkącie równobocznym.

Trójkąt prostokątny:

Twierdzenie Pitagorasa: $a^{2} + b^{2} = c^{2}$ ,

gdzie $a$ , $b$ oznaczają długości przyprostokątnych, a $c$ długość przeciwprostokątnej.

Wzory na promień okręgu wpisanego lub opisanego na trójkącie prostokątnym:

$r = p - c$ ,
$R = \frac{1}{2} c$ ,

gdzie $r$ oznacza promień okręgu wpisanego w trójkąt prostokątny, $p$ oznacza połowę obwodu, a $R$ promień okręgu opisanego na trójkącie prostokątnym.

Wzory na pole trójkąta:

$P = \frac{1}{2} a h$ ,

$P = \frac{1}{2} a b \sin α$ ,

gdzie $α$ to miara kąta pomiędzy bokami $a$ i $b$ .

Sześcian

Pole powierzchni całkowitej: $P_{c} = 6 a^{2}$ .

Objętość: $V = a^{3}$ ,
gdzie $a$ oznacza długość krawędzi sześcianu.

Skala

Wymiary rzeczywiste, to skala $1 : 1$

Skala zmniejszająca, to np. skala $1 : 2$ - wymiary zostały pomniejszone dwa razy, skala $1 : 5$ - wymiary zostały pomniejszone pięć razy.

Skala powiększająca, to np. skala $2 : 1$ - wymiary zostały powiększone dwa razy, skala $3 : 1$ - wymiary zostały powiększone trzy razy.

Procent składany

Kapitalizację odsetek obliczamy ze wzoru: $K_{n} = K \cdot {(1 + \frac{p}{100 \cdot k})}^{n \cdot k}$ ,

gdzie $K$ - kapitał początkowy, $n$ - liczba lat oszczędzania, $p$ - oprocentowanie w skali roku , $k$ - liczba kapitalizacji w ciągu roku, $K_{n}$ - kapitał zgromadzony po n latach oszczędzania.

Prawdopodobieństwo

Żeby obliczyć prawdopodobieństwo dowolnego zdarzenia (nazwijmy go literką $A$ ), musimy określić liczbę zdarzeń sprzyjających oraz liczbę wszystkich możliwych zdarzeń. Następnie korzystamy ze wzoru: $P (A) = \frac{| A |}{| Ω |}$ ,

gdzie $| A |$ - to liczba zdarzeń sprzyjających, $| Ω |$ - to liczba wszystkich możliwych zdarzeń.

Średnia arytmetyczna

Średnia arytmetyczna zbioru liczb - to suma tych liczb podzielona przez ich liczbę.

Średnia arytmetyczna liczb $x_{1}, x_{2}, x_{3}, . . ., x_{n}$ wyraża się wzorem: $\bar{x} = \frac{x_{1} + x_{2} + x_{3} + . . . + x_{n}}{n}$ .

Koło

Obwód koła obliczamy ze wzoru: $L = 2 π r$ .

Pole koła obliczamy ze wzoru: $P = π r^{2}$ .

Pole wycinka koła wyznaczonego przez kąt środkowy $α$ obliczamy ze wzoru: $P_{w} = \frac{α}{360 °} \cdot π r^{2}$ .

RKkv1AoJcPtaT

Ilustracja interaktywna 1. Pierwiastki Własności działań na pierwiastkach:
Niech

a \geq 0

b \geq 0

\sqrt{a} \cdot \sqrt{b} = \sqrt{a b}

\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}

, dla

b \neq 0

\sqrt{a^{2}} = |a|

\sqrt[m]{a^{n}} = a^{\frac{n}{m}}

, dla

n \geq 0

m > 0

., 2. Potęgi Własności działań na potęgach:
Niech

a

b

n

m

będą liczbami rzeczywistymi.

a^{m} \cdot a^{n} = a^{m + n}

a^{m} : a^{n} = a^{m - n}

, dla

a \neq 0

{(a \cdot b)}^{m} = a^{m} \cdot b^{m}

{(a : b)}^{m} = a^{m} : b^{m}

, dla

b \neq 0

{(a^{n})}^{m} = a^{m \cdot n}

., 3. Walec i kula Walec :
Wzór na pole powierzchni całkowitej:

P_{c} = 2 π r (r + H)

,
gdzie

r

oznacza promień koła w podstawie, a

H

oznacza wysokość walca.
Wzór na objętość walca:

V = π r^{2} \cdot H

Kula :
Wzór na pole powierzchni całkowitej kuli:

P_{c} = 4 π r^{2}

,
gdzie

r

oznacza promień kuli.
Objętość kuli:

V = \frac{4}{3} π r^{3}

., 4. Trójkąty Trójkąt równoboczny:
Wzór na pole:

P = \frac{a^{2} \sqrt{3}}{4}

.
Wysokość w trójkącie równobocznym:

h = \frac{a \sqrt{3}}{2}

,
gdzie

a

oznacza długość boku trójkąta.
Zależność pomiędzy wysokością a promieniem okręgu wpisanego i opisanego na trójkącie równobocznym:

r = \frac{1}{3} h

R = \frac{2}{3} h

, gdzie

r

oznacza promień okręgu wpisanego w trójkąt, a

R

promień okręgu opisanego na trójkącie równobocznym.
Trójkąt prostokątny:
Twierdzenie Pitagorasa:

a^{2} + b^{2} = c^{2}

,
gdzie

a

b

oznaczają długości przyprostokątnych, a

c

długość przeciwprostokątnej.
Wzory na promień okręgu wpisanego i opisanego na trójkącie prostokątnym:

r = p - c

R = \frac{1}{2} c

, gdzie

r

oznacza promień okręgu wpisanego w trójkąt prostokątny,

p

oznacza połowę obwodu, a

R

promień okręgu opisanego na trójkącie prostokątnym. Wzory na pole trójkąta:

P = \frac{1}{2} a h

P = \frac{1}{2} a b \sin α

, gdzie

α

to miara kąta pomiędzy bokami

a

b

., 5. Sześcian Pole powierzchni całkowitej:

P_{c} = 6 a^{2}

.
Objętość:

V = a^{3}

,
gdzie

a

oznacza długość krawędzi sześcianu., 6. Miejsce zerowe funkcji Miejsce zerowe funkcji - to taki argument

x

dla którego funkcja przyjmuje wartość

0

., 7. Skala Wymiary rzeczywiste, to skala

1 : 1

.Skala zmniejszająca, to np. skala

1 : 2

- wymiary zostały pomniejszone dwa razy, skala

1 : 5

- wymiary zostały pomniejszone pięć razy.Skala powiększająca, to np. skala

2 : 1

- wymiary zostały powiększone dwa razy, skala

3 : 1

- wymiary zostały powiększone trzy razy., 8. Procent składany Kapitalizację odsetek obliczamy ze wzoru:

K_{n} = K \cdot {(1 + \frac{p}{100 \cdot k})}^{n \cdot k}

, gdzie

K

- kapitał początkowy,

n

- liczba lat oszczędzania,

p

- oprocentowanie w skali roku ,

k

- liczba kapitalizacji w ciągu roku,

K_{n}

- kapitał zgromadzony po n latach oszczędzania., 9. Prawdopodobieństwo Żeby obliczyć prawdopodobieństwo dowolnego zdarzenia (nazwijmy go literką

A

), musimy określić liczbę zdarzeń sprzyjających oraz liczbę wszystkich możliwych zdarzeń. Następnie korzystamy ze wzoru:

P (A) = \frac{| A |}{| Ω |}

, gdzie

| A |

- to liczba zdarzeń sprzyjających,

| Ω |

- to liczba wszystkich możliwych zdarzeń., 10. Średnia arytmetyczna Średnia arytmetyczna zbioru liczb - to suma tych liczb podzielona przez ich liczbę. Średnia arytmetyczna liczb

x_{1}, x_{2}, x_{3}, . . ., x_{n}

wyraża się wzorem:

\bar{x} = \frac{x_{1} + x_{2} + x_{3} + . . . + x_{n}}{n}

., 11. Koło Obwód koła obliczamy ze wzoru:

L = 2 π r

. Pole koła obliczamy ze wzoru:

P = π r^{2}

.Pole wycinka koła wyznaczonego przez kąt środkowy

α

obliczamy ze wzoru:

P_{w} = \frac{α}{360 °} \cdot π r^{2}

Ilustracja interaktywna 1. Pierwiastki Własności działań na pierwiastkach:
Niech

a \geq 0

b \geq 0

\sqrt{a} \cdot \sqrt{b} = \sqrt{a b}

\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}

, dla

b \neq 0

\sqrt{a^{2}} = |a|

\sqrt[m]{a^{n}} = a^{\frac{n}{m}}

, dla

n \geq 0

m > 0

., 2. Potęgi Własności działań na potęgach:
Niech

a

b

n

m

będą liczbami rzeczywistymi.

a^{m} \cdot a^{n} = a^{m + n}

a^{m} : a^{n} = a^{m - n}

, dla

a \neq 0

{(a \cdot b)}^{m} = a^{m} \cdot b^{m}

{(a : b)}^{m} = a^{m} : b^{m}

, dla

b \neq 0

{(a^{n})}^{m} = a^{m \cdot n}

., 3. Walec i kula Walec :
Wzór na pole powierzchni całkowitej:

P_{c} = 2 π r (r + H)

,
gdzie

r

oznacza promień koła w podstawie, a

H

oznacza wysokość walca.
Wzór na objętość walca:

V = π r^{2} \cdot H

Kula :
Wzór na pole powierzchni całkowitej kuli:

P_{c} = 4 π r^{2}

,
gdzie

r

oznacza promień kuli.
Objętość kuli:

V = \frac{4}{3} π r^{3}

., 4. Trójkąty Trójkąt równoboczny:
Wzór na pole:

P = \frac{a^{2} \sqrt{3}}{4}

.
Wysokość w trójkącie równobocznym:

h = \frac{a \sqrt{3}}{2}

,
gdzie

a

oznacza długość boku trójkąta.
Zależność pomiędzy wysokością a promieniem okręgu wpisanego i opisanego na trójkącie równobocznym:

r = \frac{1}{3} h

R = \frac{2}{3} h

, gdzie

r

oznacza promień okręgu wpisanego w trójkąt, a

R

promień okręgu opisanego na trójkącie równobocznym.
Trójkąt prostokątny:
Twierdzenie Pitagorasa:

a^{2} + b^{2} = c^{2}

,
gdzie

a

b

oznaczają długości przyprostokątnych, a

c

długość przeciwprostokątnej.
Wzory na promień okręgu wpisanego i opisanego na trójkącie prostokątnym:

r = p - c

R = \frac{1}{2} c

, gdzie

r

oznacza promień okręgu wpisanego w trójkąt prostokątny,

p

oznacza połowę obwodu, a

R

promień okręgu opisanego na trójkącie prostokątnym. Wzory na pole trójkąta:

P = \frac{1}{2} a h

P = \frac{1}{2} a b \sin α

, gdzie

α

to miara kąta pomiędzy bokami

a

b

., 5. Sześcian Pole powierzchni całkowitej:

P_{c} = 6 a^{2}

.
Objętość:

V = a^{3}

,
gdzie

a

oznacza długość krawędzi sześcianu., 6. Miejsce zerowe funkcji Miejsce zerowe funkcji - to taki argument

x

dla którego funkcja przyjmuje wartość

0

., 7. Skala Wymiary rzeczywiste, to skala

1 : 1

.Skala zmniejszająca, to np. skala

1 : 2

- wymiary zostały pomniejszone dwa razy, skala

1 : 5

- wymiary zostały pomniejszone pięć razy.Skala powiększająca, to np. skala

2 : 1

- wymiary zostały powiększone dwa razy, skala

3 : 1

- wymiary zostały powiększone trzy razy., 8. Procent składany Kapitalizację odsetek obliczamy ze wzoru:

K_{n} = K \cdot {(1 + \frac{p}{100 \cdot k})}^{n \cdot k}

, gdzie

K

- kapitał początkowy,

n

- liczba lat oszczędzania,

p

- oprocentowanie w skali roku ,

k

- liczba kapitalizacji w ciągu roku,

K_{n}

- kapitał zgromadzony po n latach oszczędzania., 9. Prawdopodobieństwo Żeby obliczyć prawdopodobieństwo dowolnego zdarzenia (nazwijmy go literką

A

), musimy określić liczbę zdarzeń sprzyjających oraz liczbę wszystkich możliwych zdarzeń. Następnie korzystamy ze wzoru:

P (A) = \frac{| A |}{| Ω |}

, gdzie

| A |

- to liczba zdarzeń sprzyjających,

| Ω |

- to liczba wszystkich możliwych zdarzeń., 10. Średnia arytmetyczna Średnia arytmetyczna zbioru liczb - to suma tych liczb podzielona przez ich liczbę. Średnia arytmetyczna liczb

x_{1}, x_{2}, x_{3}, . . ., x_{n}

wyraża się wzorem:

\bar{x} = \frac{x_{1} + x_{2} + x_{3} + . . . + x_{n}}{n}

., 11. Koło Obwód koła obliczamy ze wzoru:

L = 2 π r

. Pole koła obliczamy ze wzoru:

P = π r^{2}

.Pole wycinka koła wyznaczonego przez kąt środkowy

α

obliczamy ze wzoru:

P_{w} = \frac{α}{360 °} \cdot π r^{2}

Źródło: GroMar, licencja: CC BY 3.0.

RbXSs0zDazz9C1

Ćwiczenie 1

Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Wyrażenie $7^{51} + 7^{50}$ ma wartość

$7^{101}$
${8 ∙ 7}^{50}$
$49^{2550}$
$14^{101}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1IcibB6epNU51

Ćwiczenie 2

Pan Maciej wpłacił do banku $2400 zł$ na lokatę roczną. Po upływie roku stan jego lokaty wzrósł do $2476,8 zł$ .
Oprocentowanie w tym banku wynosiło:

mniej niż $2,5 %$
między $2,5 %$ a $3 %$
między $3 %$ a $3,5 %$
więcej niż $3,5 %$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R156KfrSMtTpF1

Ćwiczenie 3

Średnia ocen z testu z języka angielskiego dla grupy $I$ , liczącej $10$ uczniów, wynosiła $4,2$ , a dla grupy $II$ , liczącej $15$ uczniów, wynosiła $4,6$ . Średnia ocen z tego testu dla wszystkich uczniów z obu grup była równa

$4,4$
$4,5$
$4,44$
$4,36$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1QpKGVakfSjr1

Ćwiczenie 4

Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Po usunięciu niewymierności z mianownika ułamka $\frac{\sqrt{27} - 2 \sqrt{3}}{\sqrt{3}}$ otrzymamy liczbę:

$3 \sqrt{3} - 2$
$1$
$3 - 2 \sqrt{3}$
$7$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R18KJjB1a8JUQ2

Ćwiczenie 5

W pudełku znajduje się $20$ kredek żółtych i $20$ kredek czerwonych. Aby prawdopodobieństwo wylosowania z pudełka kredki czerwonej wynosiło $0,4$ , należy

dołożyć do pudełka $10$ kredek żółtych
dołożyć do pudełka $10$ kredek czerwonych
zabrać z pudełka $8$ kredek żółtych
zabrać z pudełka $8$ kredek czerwonych

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RJI8y9hcODpCL2

Ćwiczenie 6

Ile spośród podanych liczb:

${(- \frac{1}{3})}^{- 5}, - {(- 8)}^{- 3}, {(2 \frac{3}{4})}^{- 1}, {(- 3,2)}^{- 3}$

ma dodatnią wartość?

jedna
dwie
trzy
cztery

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1LWdmFmE1SKP2

Ćwiczenie 7

W pierwszym kwartale średnia cena akcji firmy " Inter" wynosiła x zł, w drugim kwartale wzrosła o 25 zł, w trzecim stanowiła $120 %$ ceny z pierwszego kwartału, a w czwartym wynosiła $80 zł$ . Które z wyrażeń przedstawionych poniżej opisuje średnią cenę akcji firmy "Inter" w ciągu roku?

$0,8 x + 26,25$
$0,55 x + 26,25$
$3,2 x + 105$
$2,2 x + 105$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RWOySdXuUyH3n2

Ćwiczenie 8

Rozwinięcie dziesiętne ułamka $\frac{1228}{4995}$ wynosi $0,2 (458)$ .
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Na $40$ miejscu po przecinku tego rozwinięcia znajduje się cyfra:

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RNhyYiSOAthAx2

Ćwiczenie 9

W dwóch pudełkach znajdują się $64$ kule. Jeżeli z pierwszego pudełka przełożymy do drugiego $\frac{1}{9}$ liczby kul, które się w nim znajdują, to w obu pudełkach będzie taka sama liczba kul. Ile kul jest w pierwszym pudełku?

$32$
$36$
$58$
$38$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1CbHPoskRoCS2

Ćwiczenie 10

Czapka i dwa szaliki kosztują razem $90 zł$ . Cena czapki jest wyższa od ceny szalika o $20 zł$ .
Którego układu równań nie można wykorzystać do wyznaczenia ceny czapki i szalika?

$"{"\begin{matrix} x + 2 y = 90 \\ x = y + 20 \end{matrix}""$
$"{"\begin{matrix} x + 2 y = 90 \\ x = y - 20 \end{matrix}""$
$"{"\begin{matrix} 2 x + y = 90 \\ y = x + 20 \end{matrix}""$
$"{"\begin{matrix} x + 2 y = 90 \\ x - y = 20 \end{matrix}""$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RyhldjRyfwgGk2

Ćwiczenie 11

Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Dana jest funkcja określona wzorem $f (x) = \frac{5 - 10 x}{5}$ . Miejscem zerowym tej funkcji jest liczba:

$0,5$
$2$
$- 10$
$1$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RAU5X7v20XYHj2

Ćwiczenie 12

Przeciwprostokątna trójkąta prostokątnego ma długość $6$ . Miara kąta ostrego tego trójkąta jest równa $45 °$ . Pole tego trójkąta jest

większe od $15$
większe od $25$
większe od $3$
mniejsze od $10$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RlcXfC4sY4aul2

Ćwiczenie 13

Przyrząd w kształcie walca o średnicy $40 cm$ i wysokości $60 cm$ wyrównuje trawnik. Ile metrów kwadratowych powierzchni trawnika zostanie wyrównanych, jeżeli walec obróci się dwa razy? Wybierz najlepsze przybliżenie.

około $0,7 m^{2}$
około $0,8 m^{2}$
około $0,4 m^{2}$
około $1 m^{2}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RzNbEwjNEaPkc2

Ćwiczenie 14

Jeden z boków trapezu jest zarazem wysokością tego trapezu. Największy kąt wewnętrzny trapezu jest cztery razy większy od najmniejszego. Różnica miar tych kątów jest równa

$120 °$
$72 °$
$90 °$
$108 °$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1FJwwwWy7AFB2

Ćwiczenie 15

Długości boków trójkąta są równe $40, 41, 9$ . Obwód okręgu opisanego na tym trójkącie jest równy

$41 π$
$82 π$
$20 π$
$36 π$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1JAwFgCRc7CZ2

Ćwiczenie 16

Pole powierzchni całkowitej sześcianu wynosi $1$ . Objętość tego sześcianu jest równa

$6 \sqrt{6}$
$\sqrt{6}$
$\frac{\sqrt{6}}{6}$
$\frac{\sqrt{6}}{36}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RbuOjxz7KdH1S2

Ćwiczenie 17

W graniastosłupie prawidłowym trójkątnym ściany boczne są kwadratami. Suma długości krawędzi graniastosłupa jest równa $18 \sqrt{2}$ . Pole ściany bocznej jest równe

$6$
$8$
$9 \sqrt{2}$
$18$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1eQro52pB6VB2

Ćwiczenie 18

Stosunek pola powierzchni bocznej walca do pola jego przekroju osiowego jest równy

$2 π$
$π$
$2$
$4$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 19

Punkt $P$ jest środkiem koła.

R1PPo2FLTgPsv1

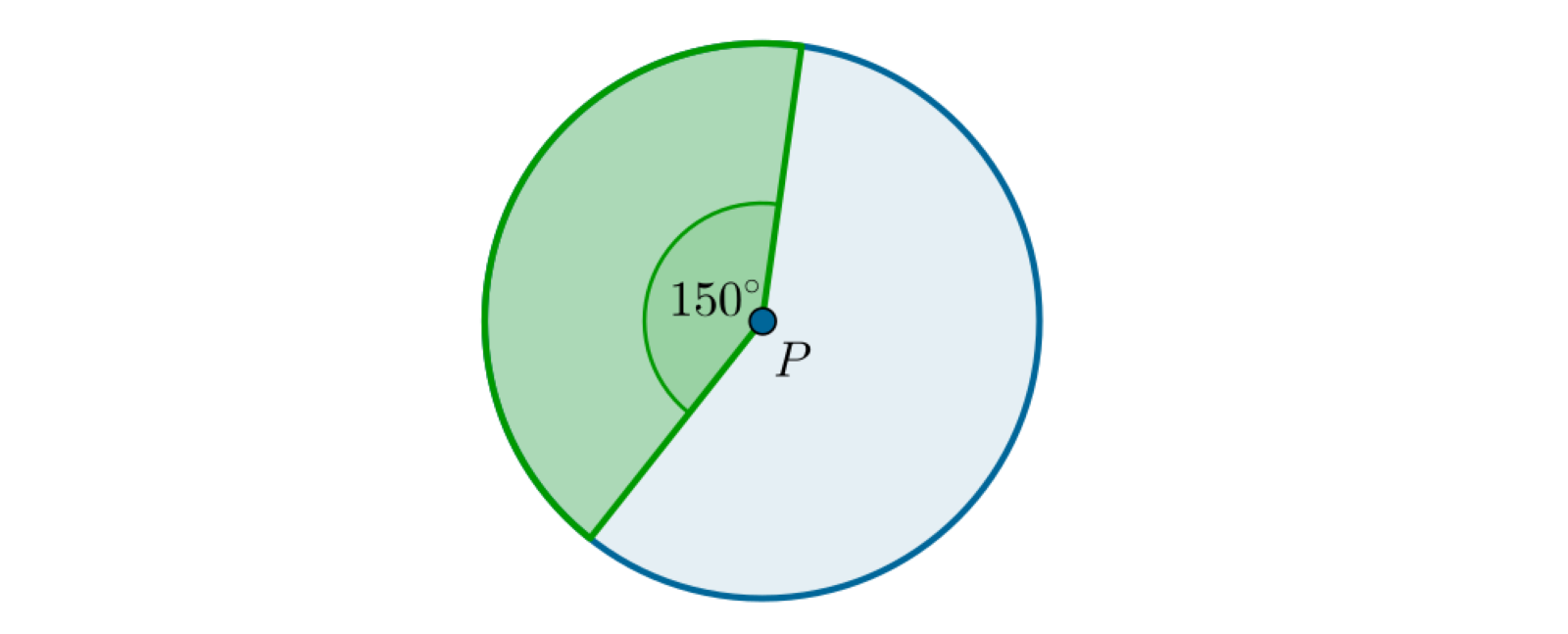
Rysunek przedstawia koło o środku P oraz mierze kąta środkowego równego 150°. Wyróżniony jest wycinek koła ograniczony łukiem i ramionami podanego kąta środkowego. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RSOLcTTVIBFLZ

$4,5$
$18$
$9$
$2,25$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R4niDSy6tx0lr3

Ćwiczenie 20

Jeśli od średniej arytmetycznej wieku Adama i Kamila, wyrażonej w latach, odejmiemy

1

, to otrzymamy wiek Maćka. Jeśli od średniej arytmetycznej wieku Adama i Maćka, również wyrażonej w latach, odejmiemy

4

, to otrzymamy wiek Kamila. Oblicz różnicę wieku między Maćkiem a Kamilem. Uzupełnij odpowiedź, wpisując w lukę odpowiednią liczbę. Odpowiedź: Różnica wieku między Maćkiem a Kamilem wynosi Tu uzupełnij lata.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RbaWmcr8V2k3I3

Ćwiczenie 21

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 22

Czworokąt $A B C D$ jest równoległobokiem. Dwusieczna kąta $A D C$ przecina bok $A B$ w punkcie $E$ , natomiast prostą, na której leży bok $B C$ w punkcie $F$ . Uzasadnij, że trójkąt $E F B$ jest równoramienny.

R1DLtY31vIhJp

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1FO0iRUu6TwX

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Narysuj opisaną sytuacje w zadaniu. Oznaczmy miarę kąta znajdującego się pomiędzy dwusieczną a bokiem $A D$ jako $α$ . Korzystając z własności kątów przy prostych równoległych miara kąta $E F B$ jest również równa $α$ . Miara kąta $D A B$ jest taka sama jak miara kąta $F B E$ . Półprosta $D E$ jest dwusieczną, więc kąt $E D C$ też ma miarę $α$ . Stąd z podobieństwa trójkątów $F D C$ i $E F B$ wynika, że miara kąta $B E F$ jest też równa alfa. Zatem trójkąt $E F B$ jest równoramienny.

Oznaczmy miarę kąta znajdującego się pomiędzy dwusieczną a bokiem $A D$ jako $α$ . Korzystając z własności kątów przy prostych równoległych miara kąta $E F B$ jest również równa $α$ . Miara kąta $D A B$ jest taka sama jak miara kąta $F B E$ . Półprosta $D E$ jest dwusieczną, więc kąt $E D C$ też ma miarę $α$ . Stąd z podobieństwa trójkątów $F D C$ i $E F B$ wynika, że miara kąta $B E F$ jest też równa alfa. Zatem trójkąt $E F B$ jest równoramienny.

ROwRNtqR5cc343

Ćwiczenie 23

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.