Zaokrąglanie liczb
W sytuacji, gdy nie potrafimy podać dokładnej wartości liczbowej wyrażenia arytmetycznego, podajemy jego przybliżenie.
W życiu codziennym dość często przybliżamy różne wielkości, np.: cenę, odległość, wzrost, wysokość, długość, wagę.
Używamy w tym celu sformułowań: około, mniej więcej, prawie, w przybliżeniu.
Film dostępny pod adresem /preview/resource/R1Z0qUxukOjk6
Animacja przedstawia kilka przykładów zaokrąglania liczb w sytuacjach praktycznych.
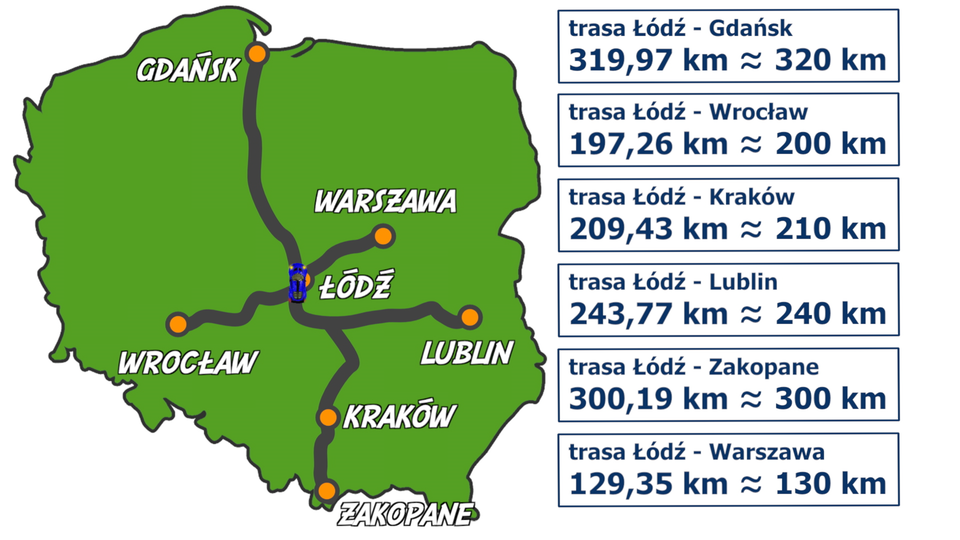
Poniżej podane są odległości drogowe między poszczególnymi miastami Polski. Zauważ, że w praktyce odległości te podawane są w kilometrach. Jest to pewnego rodzaju przybliżenie, ponieważ nie podajemy tych wartości w metrach, centymetrach czy milimetrach.
Trasa | Rzeczywista odległość | Przybliżona odległość |
|---|---|---|
Łódź – Warszawa | ||
Łódź – Lublin | ||
Łódź – Zakopane | ||
Łódź – Kraków | ||
Łódź – Gdańsk | ||
Łódź – Wrocław |
Film dostępny pod adresem /preview/resource/R1LlAZXz5pJ2P
Animacja przedstawia przybliżone odległości między planetami układu słonecznego.
Poniższa tabela przedstawia średnią odległość Słońca od planet Układu Słonecznego. (Wikipedia)
Merkury | |
|---|---|
Wenus | |
Ziemia | |
Mars | |
Jowisz | |
Saturn | |
Uran | |
Neptun |
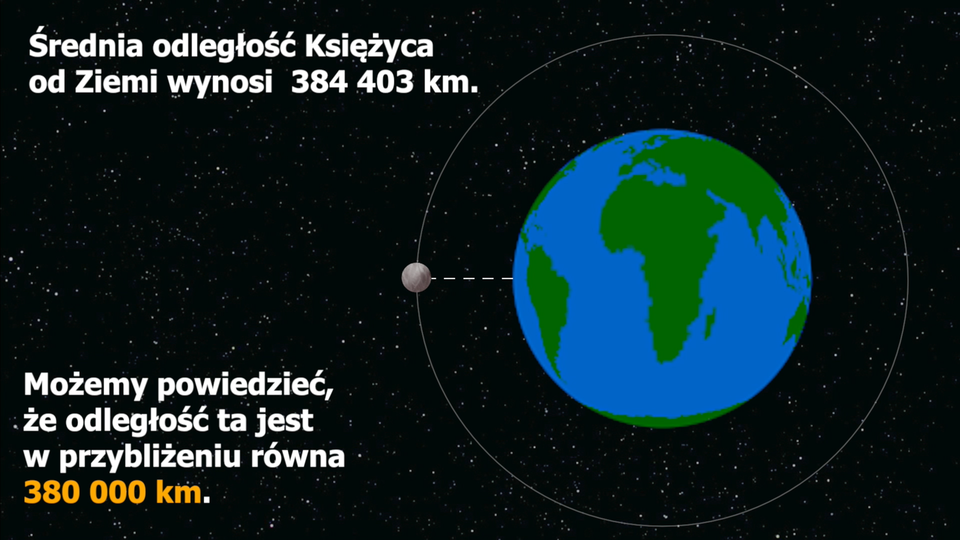
Za średnią odległość Ziemi od Słońca przyjmuje się około .
Podobnie można przyjąć, że odległość Księżyca od Ziemi wynosi około . Czasami nie da się dokonać dokładnego pomiaru danej wielkości.
Przyjmuje się, że powierzchnia Polski wynosi około , a liczba ludności jest równa około
Film dostępny pod adresem /preview/resource/R1BVyRYTs3F39
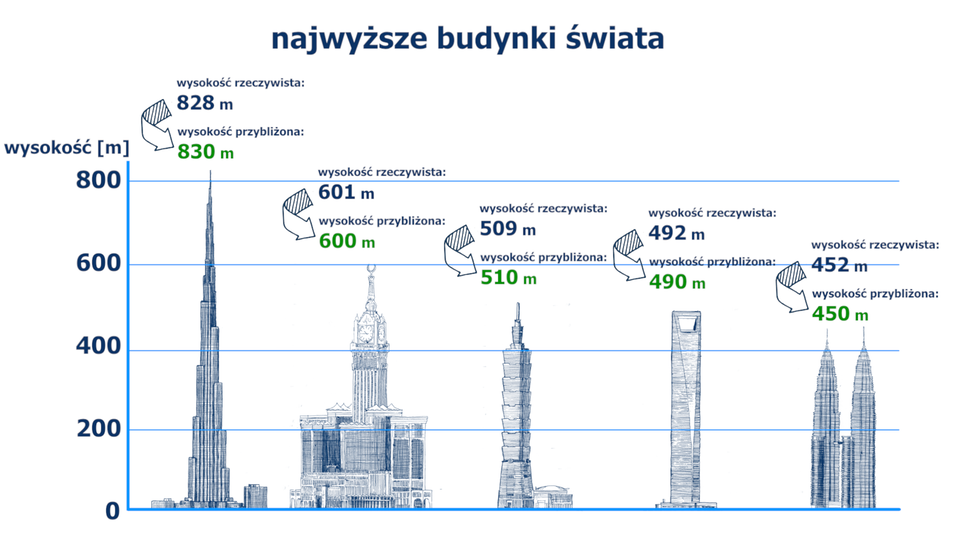
Animacja przedstawia najwyższe budynki świata.
Najwyższe budynki na świecie
Zjednoczone Emiraty Arabskie – Dubaj – Burdż Chalifa
wysokość rzeczywista – wysokość przybliżonaArabia Saudyjska – Mekka – Abraj Al Bait
wysokość rzeczywista – wysokość przybliżonaTajwan – Tajpej – Taipei
wysokość rzeczywista – wysokość przybliżonaChiny – Szanghaj - Shanghai World Financial Center
wysokość rzeczywista – wysokość przybliżona
Symbol czytamy „równa się w przybliżeniu”.

Film dostępny pod adresem /preview/resource/R1OdC50omDG22
Animacja przedstawia w jaki sposób zaokrąglamy liczby z odpowiednią dokładnością. Zaokrąglanie do dziesiątek. Zaokrągleniem do dziesiątek liczby 42 jest 40, zaokrągleniem do dziesiątek liczby 167 jest 170. Zaokrąglanie do setek. Zaokrągleniem do setek liczby 528 jest 500, zaokrągleniem do setek liczby 2863 jest 2900. Zaokrąglenie do tysięcy. Zaokrągleniem do tysięcy liczby 56497 jest 56000, zaokrągleniem do tysięcy liczby 29506 jest 30000.
Jeżeli cyfrą decydującą o wyniku zaokrąglenia, czyli stojącą w rzędzie następnym po tym, do którego przybliżamy jest , , , , , to cyfra w rzędzie, do którego przybliżamy pozostaje bez zmian, a w rzędach niższych pojawiają się zera. Mówimy, że jest to zaokrąglenie z niedomiarem ( w dół).
Jeżeli cyfrą decydującą o wyniku zaokrąglenia, czyli stojącą w rzędzie następnym po tym, do którego przybliżamy jest , , , , , a cyfra w rzędzie, do którego przybliżamy jest mniejsza od , to ta cyfra zostaje zwiększona o jeden, a w rzędach niższych pojawiają się zera. Jeżeli natomiast cyfra w rzędzie, do którego przybliżamy jest równa , to zamiast niej piszemy cyfrę i tę samą procedurę stosujemy do cyfr stojącyh w rzędach wyższych. Mówimy, że jest to zaokrąglenie z nadmiarem ( w górę).

Film dostępny pod adresem /preview/resource/R1GSY7hRcQCcV
Animacja przedstawia w jaki sposób zaokrąglamy liczby z odpowiednią dokładnością. Zaokrąglanie do jedności. Zaokrągleniem do jedności liczby 6,3 jest 6, zaokrągleniem do jedności liczby 255,84 jest 256. Zaokrąglanie do części dziesiątych. Zaokrągleniem do części dziesiątych liczby 64,098 jest 64,1, zaokrągleniem do części dziesiątych liczby 236,82 jest 236,8 . Zaokrąglenie do części setnych. Zaokrągleniem do części setnych liczby 503,895 jest 503,9, zaokrągleniem do części setnych liczby 65,3248 jest 65,32 .
Przeciagnij elementy z dolnej sekcji do górnej.
<span aria-label="dwa początek ułamka, jeden, mianownik, osiem, koniec ułamka" role="math"><math><mn>2</mn><mfrac><mn>1</mn><mn>8</mn></mfrac></math></span>, <span aria-label="dwa przecinek zero sześć trzy zero" role="math"><math> <mn>2,(63) </mn> </math></span>, <span aria-label="sześćset pięćdziesiąt dwa przecinek dwa cztery" role="math"><math> <mn> 652,24 </mn> </math></span>, <span aria-label="sześć przecinek zero sześć zero" role="math"><math> <mn> 6,(6) </mn> </math></span>, <span aria-label="sześć przecinek zero sześć dwa dziewięć zero" role="math"><math> <mn> 6,(629) </mn> </math></span>, <span aria-label="cztery początek ułamka, dwa, mianownik, siedem, koniec ułamka" role="math"><math><mn>4</mn><mfrac><mn>2</mn><mn>7</mn></mfrac></math></span>
| rozwinięcia skończone | |
|---|---|
| rozwinięcia nieskończone okresowe |
Uporządkuj liczby od najmniejszej do największej.
Tabela przedstawia odległości Słońca od planet Układu Słonecznego. Zaokrąglij liczby podane w tabeli do setek tysięcy. Uzupełnij luki.
Merkury | |
|---|---|
Wenus | |
Ziemia | |
Mars | |
Jowisz | |
Saturn | |
Uran | |
Neptun |
Poniższa tabela przedstawia średnie kursy wybranych walut zanotowane pewnego dnia.
Nazwa waluty | Kurs średni |
|---|---|
Dolar amerykański | |
Euro | |
Frank szwajcarski | |
Korona czeska | |
Lew bułgarski | |
Lira turecka | |
Lej rumuński |
Podaj przykład dwóch różnych liczb, których zaokrąglenie do części setek jest równe
,
.
Podaj przykład dwóch różnych liczb, których zaokrąglenie do części setnych jest równe
,
.
Podaj zaokrąglenia liczb zaznaczonych na osi liczbowej. Uzupełnij luki, wpisując odpowiednie wartości.
Zaokrąglij do części dziesiętnych,

Zaokrąglij do części setnych,

Zaokrąglij do setek.

1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. ,
Zaokrąglenia do części setnych
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .
Przed planowanym urlopem nad morzem rodzina Nowaków wybrała się na zakupy do centrum sportowego. Dla syna Mateusza kupili następujące akcesoria do nurkowania:
skafander za ,
kamizelkę za ,
skrzydła za ,
butlę za ,
latarkę za .
Mateusz zaokrąglił do dziesiątek złotych cenę każdego produktu i otrzymane kwoty dodał. Natomiast rodzice dodali poszczególne kwoty i dopiero otrzymaną sumę zaokrąglili do dziesiątek złotych.
Na osi liczbowej zaznaczono punkt .

Zaokrąglij współrzędną zaznaczonego na osi liczbowej punktu do podanych rzędów.

Poszukaj informacji dotyczących ludności i powierzchni w województwach sąsiadujących z województwem, w którym mieszkasz. Wartości liczbowe podaj z dokładnością do tysięcy.