Nie wszystko jest całością - ułamki zwykłe
5. Rozszerzanie oraz skaracanie ułamków
Niektóre ułamki mają bardzo ciekawe własności. Na przykład jeżeli w ułamkach
z licznika i mianownika usuniemy odpowiednio 6, 9, 3 to otrzymamy ułamki równe danym.
Sprawdź, czy w przypadku innych ułamków ten sposób postępowania również prowadzi do otrzymania ułamków równych. Zapoznaj się z poniższym materiałem i ustal, czy twoje przypuszczenia były słuszne.
W tym materiale zawarte są najważniejsze wiadomości dotyczące skracania oraz rozszerzania ułamków.
Równość ułamków
Zapoznaj się z animacją, pokazującą jak można otrzymać równe ułamki.

Film dostępny pod adresem /preview/resource/R1BPtVBVyB2IV
Animacja przedstawia kiedy dwa ułamki są sobie równe.
Na każdym talerzu znajduje się taka sama część pizzy. Ułamki opisujące te części pizzy są równe.
Zapoznaj się z animacją, która pokazuje przykład otrzymywania ułamków równych.
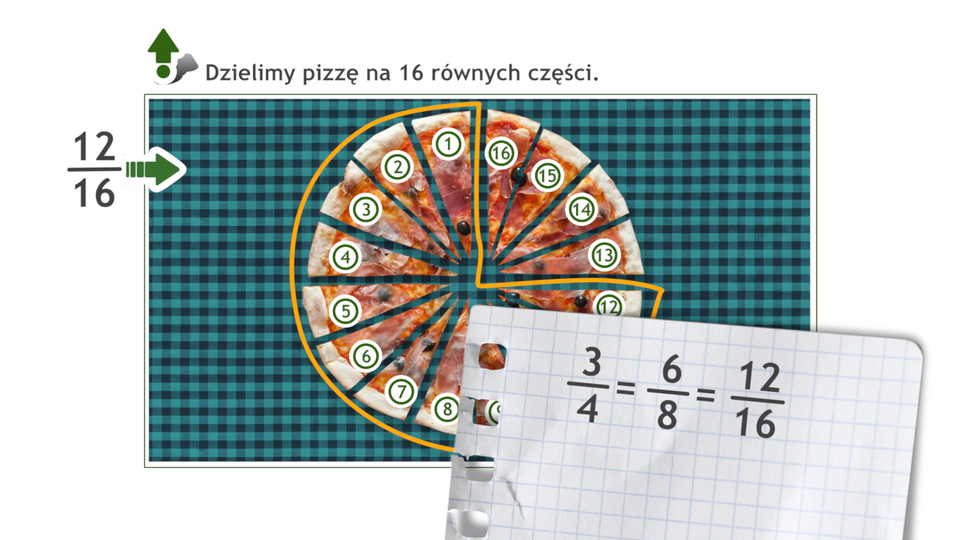
Film dostępny pod adresem /preview/resource/RG0iEEu14zuWH
Animacja przedstawia w jaki sposób możemy rozszerzać ułamki.
Dwa jednakowe kwadraty podzielono na równe części: jeden na , a drugi na części.

Na podstawie rysunku wnioskujemy, że jedna czwarta pierwszego kwadratu, to tyle samo co dwie ósme drugiego kwadratu.
Rozszerzanie ułamków
Zapoznaj się z animacją, z której dowiesz się, jak można rozszerzyć dany ułamek.
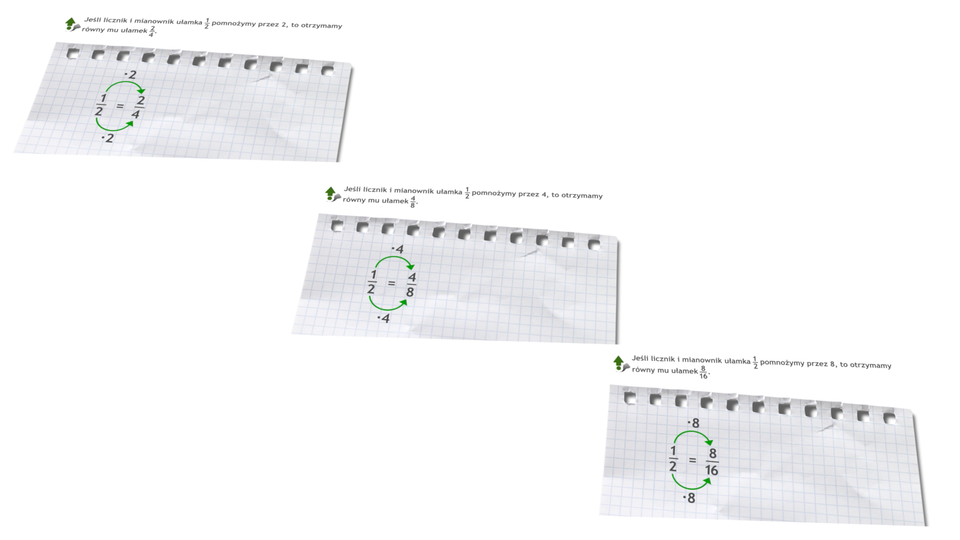
Film dostępny pod adresem /preview/resource/RnwDR7UOmZSlF
Animacja przedstawia w jaki sposób możemy rozszerzać ułamki.
Rozszerzanie ułamków polega na mnożeniu licznika i mianownika przez tę samą liczbę, różną od zera. W wyniku otrzymujemy ułamek równy danemu.
2. 1. , 2. , 3. , 4. , 5. , 6.
3. 1. , 2. , 3. , 4. , 5. , 6.
4. 1. , 2. , 3. , 4. , 5. , 6.
Przeciągnij i upuść brakujące liczniki i mianowniki tak, aby równości były prawdziwe.
, , , , , , ,
a) ............ ............ ............ ............
b) ............ ............ ............ ............
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. Rozszerz ułamki, tak aby posiadały mianownik równy .
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
- , w miejsce kropek należy wpisać Tu uzupełnij.
- , w miejsce kropek należy wpisać Tu uzupełnij.
- , w miejsce kropek należy wpisać Tu uzupełnij.
- , w miejsce kropek należy wpisać Tu uzupełnij.
- , w miejsce kropek należy wpisać Tu uzupełnij.
- , w miejsce kropek należy wpisać Tu uzupełnij.
- , w miejsce kropek należy wpisać Tu uzupełnij.
- , w miejsce kropek należy wpisać Tu uzupełnij.
- , w miejsce kropek należy wpisać Tu uzupełnij.
- , w miejsce kropek należy wpisać Tu uzupełnij.
- , w miejsce kropek należy wpisać Tu uzupełnij.
- , w miejsce kropek należy wpisać Tu uzupełnij.
oraz ,
uzupełnij luki, wpisując odpowiednie liczby. Tu uzupełnij Tu uzupełnij Tu uzupełnij Tu uzupełnij
Wiedząc, że
oraz ,
uzupełnij.
............
............
............
............
oraz ,
uzupełnij luki, wpisując odpowiednie liczby. Tu uzupełnij Tu uzupełnij Tu uzupełnij Tu uzupełnij Tu uzupełnij
Wiedząc, że
oraz ,
uzupełnij.
............
............
............
............
............
Uzupełnij brakujący licznik lub mianownik.
a) ............ b) ............
c) ............ d) ............
e) ............ f) ............
g) ............ h) ............
Skracanie ułamków
Skracanie ułamków polega na dzieleniu licznika i mianownika przez tę samą liczbę różną od zera. W wyniku otrzymujemy ułamek równy danemu.
Na przykład:

Ułamek skróciliśmy przez .
Zapoznaj się z animacją, w której zawarte są przykłady skracania ułamków.
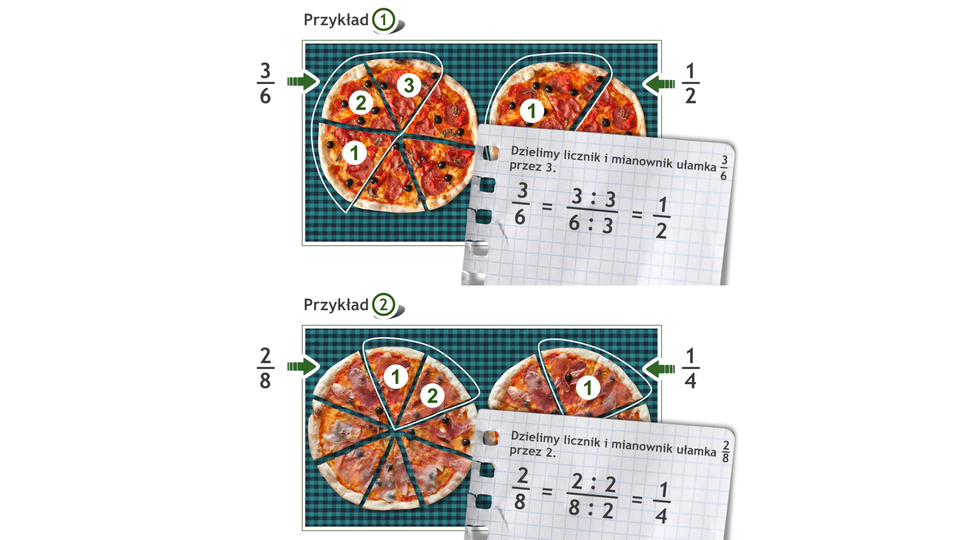
Film dostępny pod adresem /preview/resource/R1Nw061oHxp5q
Animacja przedstawia w jaki sposób możemy skracać ułamki.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
2. skróć ułamki przez
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
b) 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Przeciągnij i upuść brakujące liczniki i mianowniki tak, aby równości były prawdziwe.
, , , , , , ,
a) ............ ............ ............ ............
b) ............ ............ ............ ............
Ułamki nieskracalne
Nieraz trudno jest znaleźć największą liczbę, przez którą można skrócić dany ułamek. Na przykład, aby skrócić ułamek możemy postąpić tak:
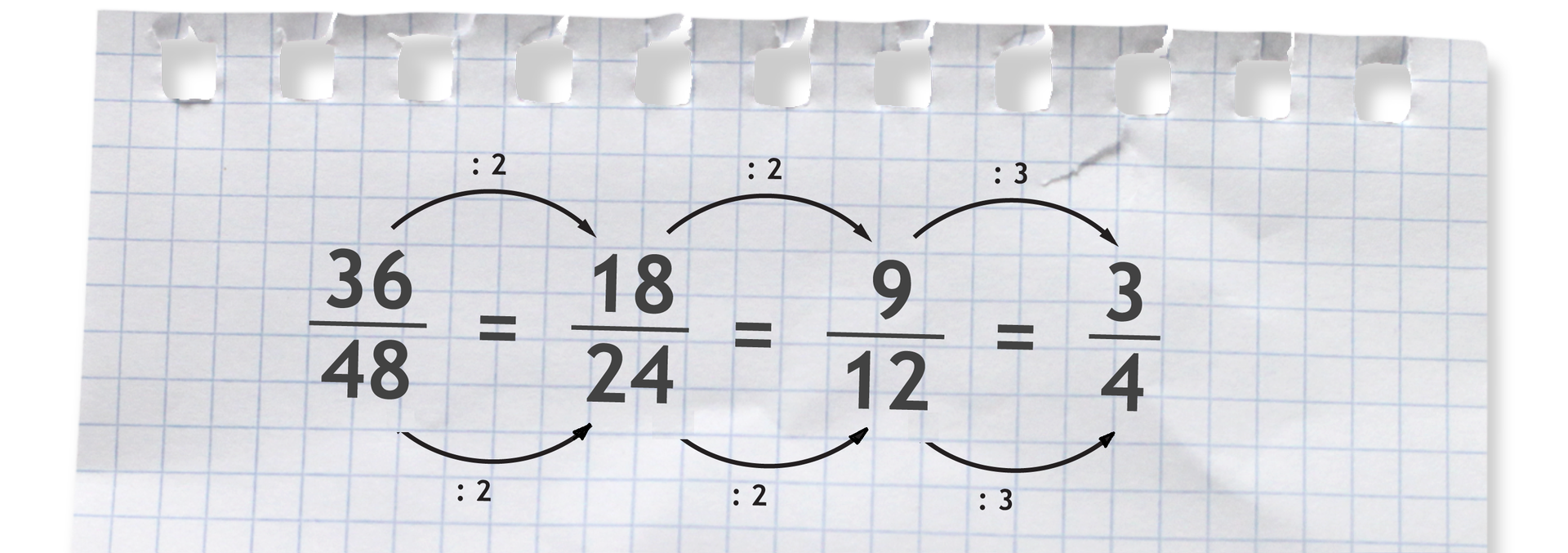
Ułamka nie można już skrócić.
Ułamek, którego nie można skrócić nazywamy ułamkiem nieskracalnym.
Zadania różne
Przeciągnij i upuść.
, , ,
............
............
............
............
Połącz w pary tak, aby brakującym elementom ułamka przyporządkować odpowiednią liczbę.
<span aria-label="początek ułamka, pięć, mianownik, osiem, koniec ułamka, równa się, początek ułamka, □, mianownik, czterdzieści osiem, koniec ułamka" role="math"><math><mfrac><mn>5</mn><mn>8</mn></mfrac><mo>=</mo><mfrac><mo>□</mo><mn>48</mn></mfrac></math></span>, <span aria-label="początek ułamka, pięć, mianownik, osiem, koniec ułamka, równa się, początek ułamka, sześćdziesiąt, mianownik, □, koniec ułamka" role="math"><math><mfrac><mn>5</mn><mn>8</mn></mfrac><mo>=</mo><mfrac><mn>60</mn><mo>□</mo></mfrac></math></span>, <span aria-label="początek ułamka, pięć, mianownik, osiem, koniec ułamka, równa się, początek ułamka, sto, mianownik, □, koniec ułamka" role="math"><math><mfrac><mn>5</mn><mn>8</mn></mfrac><mo>=</mo><mfrac><mn>100</mn><mo>□</mo></mfrac></math></span>, <span aria-label="początek ułamka, pięć, mianownik, osiem, koniec ułamka, równa się, początek ułamka, □, mianownik, szesnaście, koniec ułamka" role="math"><math><mfrac><mn>5</mn><mn>8</mn></mfrac><mo>=</mo><mfrac><mo>□</mo><mn>16</mn></mfrac></math></span>, <span aria-label="początek ułamka, pięć, mianownik, osiem, koniec ułamka, równa się, początek ułamka, □, mianownik, dwadzieścia cztery, koniec ułamka" role="math"><math><mfrac><mn>5</mn><mn>8</mn></mfrac><mo>=</mo><mfrac><mo>□</mo><mn>24</mn></mfrac></math></span>
| 10 | |
| 15 | |
| 30 | |
| 96 | |
| 160 |
Jeśli ułamek rozszerzymy przez lub przez , to otrzymamy ułamek, którego licznik i mianownik mają ciekawą własność. Jeżeli licznik przeczytamy od prawej do lewej strony, otrzymamy mianownik. Oczywiście ten sam efekt otrzymamy, gdy postąpimy podobnie z mianownikiem.
i .
Znajdź inne ułamki, które mają tę samą własność.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.