R1dZX5dLTfbs8
Zdjęcie przedstawia kompozycję złożoną z trzech połówek papai, jednego całego owocu papai, dwóch połówek pomarańczy i dwóch połówek limonki. Owoce są rozmieszczone na talerzu i obok niego. W poprzek napis na czarnym tle: nie wszystko jest całością.

Nie wszystko jest całością - ułamki zwykłe

Źródło: alleksana, domena publiczna. https://www.pexels.com/pl-pl.

6. Porównywanie ułamków

Obejrzyj poniższą animację, która pokazuje w jakich sytuacjach z życia możemy posługiwać się ułamkami.

R1UZXe9tHfDZu1
Animacja pokazuje w jakich sytuacjach z życia możemy posługiwać się ułamkami.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/R1UZXe9tHfDZu

Ulamki i liczby mieszane na osi liczbowej_atrapa_animacja_1122
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja pokazuje w jakich sytuacjach z życia możemy posługiwać się ułamkami.

Czy jedna siódma to więcej niż jedna szósta?

Czy trzy czwarte to tyle samo, co dwie trzecie?

Czy dwie dziesiąte to mniej, niż jedna piąta?

Czy siedem ósmych to więcej niż połowa?

Na tego typu pytania będziesz znać odpowiedź po zapoznaniu się z tym materiałem. Są w nim przykłady porównywania ułamków zwykłych o jednakowych licznikach lub jednakowych mianownikach. Po wykonaniu kilku utrwalających ćwiczeń, poznasz przykłady porównywania ułamków o różnych licznikach i różnych mianownikach. Rozwiązując ćwiczenia końcowe – sprawdzisz ukształtowane umiejętności.

Ważne!

Ułamki zwykłe, podobnie jak wszystkie inne liczby, można ze sobą porównywać. Jeżeli ułamki, które chcemy porównać, możemy tak skrócić lub rozszerzyć, że w obu przypadkach otrzymamy ten sam ułamek, to porównywane ułamki są równe. Na przykład:

915=2135, ponieważ 915=35 oraz 2135=35.

Porównywanie ułamków o jednakowych licznikach

R1VA1pwIA2OwP1
Animacja przedstawia jak porównujemy ułamki o jednakowych licznikach.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/R1VA1pwIA2OwP

Porownywanie ulamkow o jednakowych licznikach lub mianownikach_atrapa_animacja_199
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia jak porównujemy ułamki o jednakowych licznikach.

Ważne!

Jeżeli dwa ułamki mają równe liczniki, to większy z nich jest ten, który ma mniejszy mianownik.

Na przykład 514>521.

Ułamki te mają równe liczniki. Mianownik 14 jest mniejszy niż mianownik 21, a więc ułamek 514 jest większy niż 521.

RFB2bjGDiSm20
Ćwiczenie 1
Uzupełnij poniższe nierówności, przeciągając w luki odpowiednie znaki. 161. >, 2. <, 3. >, 4. <, 5. >, 6. =, 7. <, 8. =, 9. =, 10. <, 11. =, 12. <, 13. >, 14. >, 15. =18 581. >, 2. <, 3. >, 4. <, 5. >, 6. =, 7. <, 8. =, 9. =, 10. <, 11. =, 12. <, 13. >, 14. >, 15. =56 471. >, 2. <, 3. >, 4. <, 5. >, 6. =, 7. <, 8. =, 9. =, 10. <, 11. =, 12. <, 13. >, 14. >, 15. =45 561. >, 2. <, 3. >, 4. <, 5. >, 6. =, 7. <, 8. =, 9. =, 10. <, 11. =, 12. <, 13. >, 14. >, 15. =59 561. >, 2. <, 3. >, 4. <, 5. >, 6. =, 7. <, 8. =, 9. =, 10. <, 11. =, 12. <, 13. >, 14. >, 15. =1518
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R9CIhotbkyS6d
Ćwiczenie 2
Uzupełnij poniższe nierówności, przeciągając w luki odpowiednie znaki. 791. <, 2. =, 3. >, 4. >, 5. >, 6. <, 7. <, 8. <, 9. =, 10. >, 11. =, 12. <, 13. =, 14. <, 15. >, 16. >, 17. >, 18. >, 19. =, 20. =, 21. =, 22. =, 23. <, 24. <711 121. <, 2. =, 3. >, 4. >, 5. >, 6. <, 7. <, 8. <, 9. =, 10. >, 11. =, 12. <, 13. =, 14. <, 15. >, 16. >, 17. >, 18. >, 19. =, 20. =, 21. =, 22. =, 23. <, 24. <13 2191. <, 2. =, 3. >, 4. >, 5. >, 6. <, 7. <, 8. <, 9. =, 10. >, 11. =, 12. <, 13. =, 14. <, 15. >, 16. >, 17. >, 18. >, 19. =, 20. =, 21. =, 22. =, 23. <, 24. <217 8111. <, 2. =, 3. >, 4. >, 5. >, 6. <, 7. <, 8. <, 9. =, 10. >, 11. =, 12. <, 13. =, 14. <, 15. >, 16. >, 17. >, 18. >, 19. =, 20. =, 21. =, 22. =, 23. <, 24. <811 10251. <, 2. =, 3. >, 4. >, 5. >, 6. <, 7. <, 8. <, 9. =, 10. >, 11. =, 12. <, 13. =, 14. <, 15. >, 16. >, 17. >, 18. >, 19. =, 20. =, 21. =, 22. =, 23. <, 24. <10100 15271. <, 2. =, 3. >, 4. >, 5. >, 6. <, 7. <, 8. <, 9. =, 10. >, 11. =, 12. <, 13. =, 14. <, 15. >, 16. >, 17. >, 18. >, 19. =, 20. =, 21. =, 22. =, 23. <, 24. <15211 13541. <, 2. =, 3. >, 4. >, 5. >, 6. <, 7. <, 8. <, 9. =, 10. >, 11. =, 12. <, 13. =, 14. <, 15. >, 16. >, 17. >, 18. >, 19. =, 20. =, 21. =, 22. =, 23. <, 24. <1345 371. <, 2. =, 3. >, 4. >, 5. >, 6. <, 7. <, 8. <, 9. =, 10. >, 11. =, 12. <, 13. =, 14. <, 15. >, 16. >, 17. >, 18. >, 19. =, 20. =, 21. =, 22. =, 23. <, 24. <1228
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1CH8WlIdvXZe
Ćwiczenie 3
Uzupełnij nierówności, przeciągając w luki odpowiednie znaki lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 591. <, 2. =, 3. =, 4. <, 5. >, 6. <, 7. >, 8. =, 9. <, 10. >, 11. <, 12. =, 13. =, 14. <, 15. =, 16. <, 17. >, 18. =, 19. >, 20. >, 21. >511 171. <, 2. =, 3. =, 4. <, 5. >, 6. <, 7. >, 8. =, 9. <, 10. >, 11. <, 12. =, 13. =, 14. <, 15. =, 16. <, 17. >, 18. =, 19. >, 20. >, 21. >18 5191. <, 2. =, 3. =, 4. <, 5. >, 6. <, 7. >, 8. =, 9. <, 10. >, 11. <, 12. =, 13. =, 14. <, 15. =, 16. <, 17. >, 18. =, 19. >, 20. >, 21. >517 8511. <, 2. =, 3. =, 4. <, 5. >, 6. <, 7. >, 8. =, 9. <, 10. >, 11. <, 12. =, 13. =, 14. <, 15. =, 16. <, 17. >, 18. =, 19. >, 20. >, 21. >851 10201. <, 2. =, 3. =, 4. <, 5. >, 6. <, 7. >, 8. =, 9. <, 10. >, 11. <, 12. =, 13. =, 14. <, 15. =, 16. <, 17. >, 18. =, 19. >, 20. >, 21. >1010 15491. <, 2. =, 3. =, 4. <, 5. >, 6. <, 7. >, 8. =, 9. <, 10. >, 11. <, 12. =, 13. =, 14. <, 15. =, 16. <, 17. >, 18. =, 19. >, 20. >, 21. >1548 13541. <, 2. =, 3. =, 4. <, 5. >, 6. <, 7. >, 8. =, 9. <, 10. >, 11. <, 12. =, 13. =, 14. <, 15. =, 16. <, 17. >, 18. =, 19. >, 20. >, 21. >1345
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1UOtgLTSKD2o
Ćwiczenie 4
Uzupełnij nierówności, przeciągając w luki odpowiednie znaki lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 4591. <, 2. <, 3. <, 4. >, 5. >, 6. >, 7. <, 8. =, 9. =, 10. =, 11. =, 12. >557 16171. <, 2. <, 3. <, 4. >, 5. >, 6. >, 7. <, 8. =, 9. =, 10. =, 11. =, 12. >1623 30381. <, 2. <, 3. <, 4. >, 5. >, 6. >, 7. <, 8. =, 9. =, 10. =, 11. =, 12. >30310 148131. <, 2. <, 3. <, 4. >, 5. >, 6. >, 7. <, 8. =, 9. =, 10. =, 11. =, 12. >14815
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 5

Któremu  ułamkowi odpowiada punkt na osi liczbowej położony dalej od punktu odpowiadającego liczbie  jeden : 38 czy 39?

R1X5p7YayahVG1
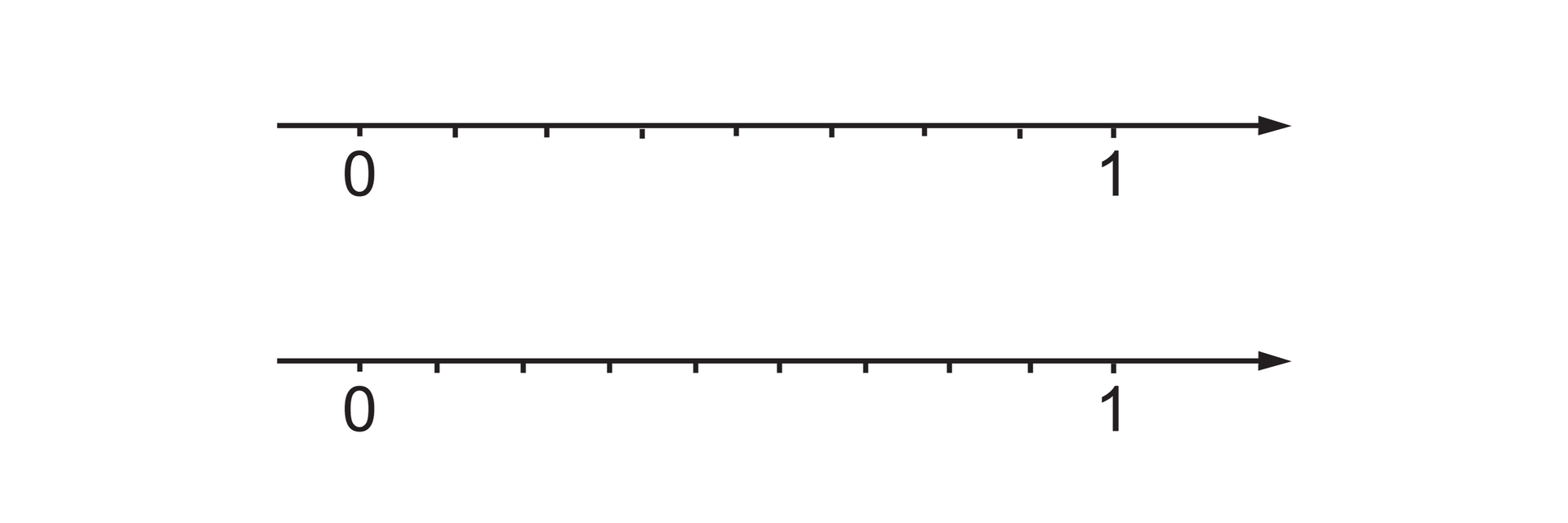
Rysunek dwóch osi liczbowych z zaznaczonymi punktami 0 i 1. Na pierwszej osi odcinek jednostkowy podzielony na osiem równych części. Na drugiej osi odcinek jednostkowy podzielony na dziewięć równych części.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
REyscJJbxBn9Z
Zaznacz poprawne zakończenie zdania. Dalej od liczby 1 na osi liczbowej jest liczba Możliwe odpowiedzi: 1. 39., 2. 38.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Porównywanie ułamków o jednakowych mianownikach

RKHjnivDKTMPL1
Animacja przedstawia jak porównujemy ułamki o jednakowych mianownikach.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/RKHjnivDKTMPL

Porownywanie ulamkow o jednakowych licznikach lub mianownikach_atrapa_animacja_200
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia jak porównujemy ułamki o jednakowych mianownikach.

Porównywanie ułamków nie sprawia kłopotów, jeżeli zaznaczy się je na osi liczbowej.

Przykład 1

Przypomnijmy, jak zaznaczać ułamki na osi liczbowej.

RwXDFbzMwMksp1
Animacja przedstawia, w jaki sposób porównujemy ułamki znajdujące się na osi liczbowej.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/RwXDFbzMwMksp

Ulamki i liczby mieszane na osi liczbowej_atrapa_animacja_1126
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia, w jaki sposób porównujemy ułamki znajdujące się na osi liczbowej.

Ważne!

Jeżeli dwa ułamki mają równe mianowniki, to większym z nich jest ten, który ma większy licznik. Na przykład:

723>523

Ułamki te mają równe mianowniki. Licznik 7 jest większy niż licznik 5, a więc ułamek 723 jest większy niż 523.

Rj9s0egVw1Uf9
Ćwiczenie 6
Uzupełnij poniższe nierówności, przeciągając w luki odpowiednie znaki. 351. =, 2. <, 3. =, 4. =, 5. =, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. >, 13. <, 14. =, 15. <, 16. >, 17. >, 18. >45 6131. =, 2. <, 3. =, 4. =, 5. =, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. >, 13. <, 14. =, 15. <, 16. >, 17. >, 18. >713 271. =, 2. <, 3. =, 4. =, 5. =, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. >, 13. <, 14. =, 15. <, 16. >, 17. >, 18. >57 591. =, 2. <, 3. =, 4. =, 5. =, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. >, 13. <, 14. =, 15. <, 16. >, 17. >, 18. >39 9101. =, 2. <, 3. =, 4. =, 5. =, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. >, 13. <, 14. =, 15. <, 16. >, 17. >, 18. >810 561. =, 2. <, 3. =, 4. =, 5. =, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. >, 13. <, 14. =, 15. <, 16. >, 17. >, 18. >16
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Rm22RdevWBX4H
Ćwiczenie 7
Uzupełnij nierówności, przeciągając w luki odpowiednie znaki lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 3161. <, 2. >, 3. =, 4. =, 5. <, 6. >, 7. =, 8. <, 9. >, 10. =, 11. >, 12. >, 13. <, 14. <, 15. = 416 6191. <, 2. >, 3. =, 4. =, 5. <, 6. >, 7. =, 8. <, 9. >, 10. =, 11. >, 12. >, 13. <, 14. <, 15. = 719 2711. <, 2. >, 3. =, 4. =, 5. <, 6. >, 7. =, 8. <, 9. >, 10. =, 11. >, 12. >, 13. <, 14. <, 15. = 571 5931. <, 2. >, 3. =, 4. =, 5. <, 6. >, 7. =, 8. <, 9. >, 10. =, 11. >, 12. >, 13. <, 14. <, 15. = 393 91001. <, 2. >, 3. =, 4. =, 5. <, 6. >, 7. =, 8. <, 9. >, 10. =, 11. >, 12. >, 13. <, 14. <, 15. = 8100
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RmP7M5I2Kgy5J1
Ćwiczenie 8
Uzupełnij zdania, przeciągając w luki odpowiednie słowa. Jeżeli dwa ułamki mają równe mianowniki, to większym z nich jest ten, który ma 1. większy, 2. mniejszy, 3. mniejszy, 4. większy licznik. Jeżeli dwa ułamki mają równe liczniki, to większym z nich jest ten, który ma 1. większy, 2. mniejszy, 3. mniejszy, 4. większy mianownik.

Wybierz.

mniejszy, mniejszy, większy, większy

Jeżeli dwa ułamki mają równe mianowniki, to większym z nich jest ten, który ma ................ licznik.

Jeżeli dwa ułamki mają równe liczniki, to większym z nich jest ten, który ma ................ mianownik.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1HwXhB60UaVT
Ćwiczenie 9
Janek i Paweł dostali od rodziców po tyle samo pieniędzy na swoje wydatki. Janek wydał 59 otrzymanej kwoty, a Paweł tyle, że zostało mu 59 pieniędzy otrzymanych od rodziców.
Uzupełnij zdania, przeciągając w luki odpowiednie słowa lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Więcej pieniędzy wydał 1. Jankowi, 2. Janek, 3. Pawłowi, 4. Paweł. Więcej pieniędzy zostało 1. Jankowi, 2. Janek, 3. Pawłowi, 4. Paweł.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RjH8zm6oaHdUj
Ćwiczenie 10
Uzupełnij nierówności, przeciągając w luki odpowiednie znaki lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 2 3151. =, 2. =, 3. <, 4. <, 5. >, 6. <, 7. >, 8. <, 9. >, 10. =, 11. >, 12. =2 415 12 8131. =, 2. =, 3. <, 4. <, 5. >, 6. <, 7. >, 8. <, 9. >, 10. =, 11. >, 12. = 11913 412271. =, 2. =, 3. <, 4. <, 5. >, 6. <, 7. >, 8. <, 9. >, 10. =, 11. >, 12. =41 527 345341. =, 2. =, 3. <, 4. <, 5. >, 6. <, 7. >, 8. <, 9. >, 10. =, 11. >, 12. = 43334
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R12hstXJ53ogJ
Ćwiczenie 11
Uzupełnij poniższe nierówności, przeciągając w luki odpowiednie znaki. 3351. >, 2. >, 3. =, 4. <, 5. <, 6. =, 7. >, 8. >, 9. <, 10. >, 11. =, 12. =, 13. =, 14. <, 15. >, 16. =, 17. <, 18. <, 19. =, 20. >, 21. <345 26131. >, 2. >, 3. =, 4. <, 5. <, 6. =, 7. >, 8. >, 9. <, 10. >, 11. =, 12. =, 13. =, 14. <, 15. >, 16. =, 17. <, 18. <, 19. =, 20. >, 21. <1713 31271. >, 2. >, 3. =, 4. <, 5. <, 6. =, 7. >, 8. >, 9. <, 10. >, 11. =, 12. =, 13. =, 14. <, 15. >, 16. =, 17. <, 18. <, 19. =, 20. >, 21. <3157 245141. >, 2. >, 3. =, 4. <, 5. <, 6. =, 7. >, 8. >, 9. <, 10. >, 11. =, 12. =, 13. =, 14. <, 15. >, 16. =, 17. <, 18. <, 19. =, 20. >, 21. <24314 107101. >, 2. >, 3. =, 4. <, 5. <, 6. =, 7. >, 8. >, 9. <, 10. >, 11. =, 12. =, 13. =, 14. <, 15. >, 16. =, 17. <, 18. <, 19. =, 20. >, 21. <10810 15561. >, 2. >, 3. =, 4. <, 5. <, 6. =, 7. >, 8. >, 9. <, 10. >, 11. =, 12. =, 13. =, 14. <, 15. >, 16. =, 17. <, 18. <, 19. =, 20. >, 21. <1516 1556271. >, 2. >, 3. =, 4. <, 5. <, 6. =, 7. >, 8. >, 9. <, 10. >, 11. =, 12. =, 13. =, 14. <, 15. >, 16. =, 17. <, 18. <, 19. =, 20. >, 21. <1514627
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Porównywanie ułamków o różnych licznikach i mianownikach

Ważne!

Aby porównać dwa ułamki o różnych licznikach i różnych mianownikach, należy sprowadzić je najpierw do wspólnego mianownika (lub licznika).  

R1el1uBwCWjBw
Ćwiczenie 12
Zaznacz wszystkie pary równych ułamków. Możliwe odpowiedzi: 1. 915, 610, 2. 1821, 97, 3. 19, 545, 4. 2464, 616

  • 915, 610
  • 1821, 97
  • 19, 545
  • 2464, 616
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R13GMH6Hso4qj
Ćwiczenie 13
Janek, Bolek i Tolek mieli po tyle samo ołówków z gumką. Janek oddał koleżankom 29 swoich ołówków, Bolek 39 swoich, a Tolek 25 swoich.
Wskaż wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Bolek oddał więcej ołówków niż Janek., 2. Tolek oddał więcej ołówków niż Bolek., 3. Janek oddał więcej ołówków niż Tolek., 4. Najwięcej ołówków zostało Jankowi.

  • Bolek oddał więcej ołówków niż Janek.
  • Tolek oddał więcej ołówków niż Bolek.
  • Janek oddał więcej ołówków niż Tolek.
  • Najwięcej ołówków zostało Jankowi.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1buhWJ55BtRP
Ćwiczenie 14
Uzupełnij poniższe nierówności, przeciągając w luki odpowiednie znaki. 13151. <, 2. >, 3. >, 4. <, 5. =, 6. =, 7. <, 8. =, 9. >, 10. =, 11. <, 12. >, 13. >, 14. >, 15. >, 16. <, 17. =, 18. <, 19. <, 20. =, 21. =1345 216171. <, 2. >, 3. >, 4. <, 5. =, 6. =, 7. <, 8. =, 9. >, 10. =, 11. <, 12. >, 13. >, 14. >, 15. >, 16. <, 17. =, 18. <, 19. <, 20. =, 21. =21619 412171. <, 2. >, 3. >, 4. <, 5. =, 6. =, 7. <, 8. =, 9. >, 10. =, 11. <, 12. >, 13. >, 14. >, 15. >, 16. <, 17. =, 18. <, 19. <, 20. =, 21. =41517 243141. <, 2. >, 3. >, 4. <, 5. =, 6. =, 7. <, 8. =, 9. >, 10. =, 11. <, 12. >, 13. >, 14. >, 15. >, 16. <, 17. =, 18. <, 19. <, 20. =, 21. =24319 199101. <, 2. >, 3. >, 4. <, 5. =, 6. =, 7. <, 8. =, 9. >, 10. =, 11. <, 12. >, 13. >, 14. >, 15. >, 16. <, 17. =, 18. <, 19. <, 20. =, 21. =19810 45171. <, 2. >, 3. >, 4. <, 5. =, 6. =, 7. <, 8. =, 9. >, 10. =, 11. <, 12. >, 13. >, 14. >, 15. >, 16. <, 17. =, 18. <, 19. <, 20. =, 21. =4516 15146271. <, 2. >, 3. >, 4. <, 5. =, 6. =, 7. <, 8. =, 9. >, 10. =, 11. <, 12. >, 13. >, 14. >, 15. >, 16. <, 17. =, 18. <, 19. <, 20. =, 21. =1514627
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RRkKW6kmdqJ1i
Ćwiczenie 15
Sprowadź ułamki do wspólnego mianownika, a następnie porównaj je. Uzupełnij równości i nierówności, przeciągając w luki odpowiednie liczby i znaki lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 35=1. <, 2. 1115, 3. 1718, 4. >, 5. 1518, 6. <, 7. >, 8. 2124, 9. >, 10. 1618, 11. 2024, 12. 1924, 13. <, 14. 915, 15. 1015, 23=1. <, 2. 1115, 3. 1718, 4. >, 5. 1518, 6. <, 7. >, 8. 2124, 9. >, 10. 1618, 11. 2024, 12. 1924, 13. <, 14. 915, 15. 1015, więc 351. <, 2. 1115, 3. 1718, 4. >, 5. 1518, 6. <, 7. >, 8. 2124, 9. >, 10. 1618, 11. 2024, 12. 1924, 13. <, 14. 915, 15. 101523 78=1. <, 2. 1115, 3. 1718, 4. >, 5. 1518, 6. <, 7. >, 8. 2124, 9. >, 10. 1618, 11. 2024, 12. 1924, 13. <, 14. 915, 15. 1015, 56=1. <, 2. 1115, 3. 1718, 4. >, 5. 1518, 6. <, 7. >, 8. 2124, 9. >, 10. 1618, 11. 2024, 12. 1924, 13. <, 14. 915, 15. 1015, więc 781. <, 2. 1115, 3. 1718, 4. >, 5. 1518, 6. <, 7. >, 8. 2124, 9. >, 10. 1618, 11. 2024, 12. 1924, 13. <, 14. 915, 15. 101556 56=1. <, 2. 1115, 3. 1718, 4. >, 5. 1518, 6. <, 7. >, 8. 2124, 9. >, 10. 1618, 11. 2024, 12. 1924, 13. <, 14. 915, 15. 1015, 89=1. <, 2. 1115, 3. 1718, 4. >, 5. 1518, 6. <, 7. >, 8. 2124, 9. >, 10. 1618, 11. 2024, 12. 1924, 13. <, 14. 915, 15. 1015, więc 561. <, 2. 1115, 3. 1718, 4. >, 5. 1518, 6. <, 7. >, 8. 2124, 9. >, 10. 1618, 11. 2024, 12. 1924, 13. <, 14. 915, 15. 101589
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1DqeLLtOmqIM
Ćwiczenie 16
Sprowadź ułamki do wspólnego licznika, a następnie porównaj je. Uzupełnij równości i nierówności, przeciągając w luki odpowiednie liczby i znaki lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 35=1. <, 2. 4048, 3. 68, 4. 3540, 5. >, 6. 4047, 7. <, 8. <, 9. 610, 10. 3541, 11. 3542, 12. 69, 13. 4045, 14. >, 15. >, 23=1. <, 2. 4048, 3. 68, 4. 3540, 5. >, 6. 4047, 7. <, 8. <, 9. 610, 10. 3541, 11. 3542, 12. 69, 13. 4045, 14. >, 15. >, więc 351. <, 2. 4048, 3. 68, 4. 3540, 5. >, 6. 4047, 7. <, 8. <, 9. 610, 10. 3541, 11. 3542, 12. 69, 13. 4045, 14. >, 15. >23 78=1. <, 2. 4048, 3. 68, 4. 3540, 5. >, 6. 4047, 7. <, 8. <, 9. 610, 10. 3541, 11. 3542, 12. 69, 13. 4045, 14. >, 15. >, 56=1. <, 2. 4048, 3. 68, 4. 3540, 5. >, 6. 4047, 7. <, 8. <, 9. 610, 10. 3541, 11. 3542, 12. 69, 13. 4045, 14. >, 15. >, więc 781. <, 2. 4048, 3. 68, 4. 3540, 5. >, 6. 4047, 7. <, 8. <, 9. 610, 10. 3541, 11. 3542, 12. 69, 13. 4045, 14. >, 15. >56 89=1. <, 2. 4048, 3. 68, 4. 3540, 5. >, 6. 4047, 7. <, 8. <, 9. 610, 10. 3541, 11. 3542, 12. 69, 13. 4045, 14. >, 15. >, 56=1. <, 2. 4048, 3. 68, 4. 3540, 5. >, 6. 4047, 7. <, 8. <, 9. 610, 10. 3541, 11. 3542, 12. 69, 13. 4045, 14. >, 15. >, więc 891. <, 2. 4048, 3. 68, 4. 3540, 5. >, 6. 4047, 7. <, 8. <, 9. 610, 10. 3541, 11. 3542, 12. 69, 13. 4045, 14. >, 15. >56
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Rw6444kzcoHQb
Ćwiczenie 17
Sprowadź ułamki do wspólnego mianownika, a następnie uzupełnij nierówności, przeciągając w luki odpowiednie znaki lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 341. >, 2. >, 3. >, 4. =, 5. >, 6. =, 7. >, 8. >, 9. =, 10. >, 11. <, 12. <, 13. =, 14. <, 15. <, 16. >, 17. <, 18. =, 19. <, 20. =, 21. <, 22. =, 23. =, 24. < 23 181. >, 2. >, 3. >, 4. =, 5. >, 6. =, 7. >, 8. >, 9. =, 10. >, 11. <, 12. <, 13. =, 14. <, 15. <, 16. >, 17. <, 18. =, 19. <, 20. =, 21. <, 22. =, 23. =, 24. < 215 7101. >, 2. >, 3. >, 4. =, 5. >, 6. =, 7. >, 8. >, 9. =, 10. >, 11. <, 12. <, 13. =, 14. <, 15. <, 16. >, 17. <, 18. =, 19. <, 20. =, 21. <, 22. =, 23. =, 24. < 68 5121. >, 2. >, 3. >, 4. =, 5. >, 6. =, 7. >, 8. >, 9. =, 10. >, 11. <, 12. <, 13. =, 14. <, 15. <, 16. >, 17. <, 18. =, 19. <, 20. =, 21. <, 22. =, 23. =, 24. < 46 15181. >, 2. >, 3. >, 4. =, 5. >, 6. =, 7. >, 8. >, 9. =, 10. >, 11. <, 12. <, 13. =, 14. <, 15. <, 16. >, 17. <, 18. =, 19. <, 20. =, 21. <, 22. =, 23. =, 24. < 3037 371. >, 2. >, 3. >, 4. =, 5. >, 6. =, 7. >, 8. >, 9. =, 10. >, 11. <, 12. <, 13. =, 14. <, 15. <, 16. >, 17. <, 18. =, 19. <, 20. =, 21. <, 22. =, 23. =, 24. < 821 591. >, 2. >, 3. >, 4. =, 5. >, 6. =, 7. >, 8. >, 9. =, 10. >, 11. <, 12. <, 13. =, 14. <, 15. <, 16. >, 17. <, 18. =, 19. <, 20. =, 21. <, 22. =, 23. =, 24. < 1527 8161. >, 2. >, 3. >, 4. =, 5. >, 6. =, 7. >, 8. >, 9. =, 10. >, 11. <, 12. <, 13. =, 14. <, 15. <, 16. >, 17. <, 18. =, 19. <, 20. =, 21. <, 22. =, 23. =, 24. < 1633
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RJHqBtp3FaPDd
Ćwiczenie 18
Uzupełnij nierówności, przeciągając w luki odpowiednie znaki lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 3 231. =, 2. <, 3. <, 4. <, 5. <, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. =, 13. =, 14. <, 15. =, 16. >, 17. =, 18. >, 19. >, 20. >, 21. >, 22. =, 23. =, 24. > 3 610 12 171. =, 2. <, 3. <, 4. <, 5. <, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. =, 13. =, 14. <, 15. =, 16. >, 17. =, 18. >, 19. >, 20. >, 21. >, 22. =, 23. =, 24. > 12 215 9 3101. =, 2. <, 3. <, 4. <, 5. <, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. =, 13. =, 14. <, 15. =, 16. >, 17. =, 18. >, 19. >, 20. >, 21. >, 22. =, 23. =, 24. > 9 38 4 5121. =, 2. <, 3. <, 4. <, 5. <, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. =, 13. =, 14. <, 15. =, 16. >, 17. =, 18. >, 19. >, 20. >, 21. >, 22. =, 23. =, 24. > 3 36 25 15191. =, 2. <, 3. <, 4. <, 5. <, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. =, 13. =, 14. <, 15. =, 16. >, 17. =, 18. >, 19. >, 20. >, 21. >, 22. =, 23. =, 24. > 25 3038 11 381. =, 2. <, 3. <, 4. <, 5. <, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. =, 13. =, 14. <, 15. =, 16. >, 17. =, 18. >, 19. >, 20. >, 21. >, 22. =, 23. =, 24. > 11 824 5 16481. =, 2. <, 3. <, 4. <, 5. <, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. =, 13. =, 14. <, 15. =, 16. >, 17. =, 18. >, 19. >, 20. >, 21. >, 22. =, 23. =, 24. > 5 13 7 8161. =, 2. <, 3. <, 4. <, 5. <, 6. >, 7. =, 8. >, 9. <, 10. <, 11. <, 12. =, 13. =, 14. <, 15. =, 16. >, 17. =, 18. >, 19. >, 20. >, 21. >, 22. =, 23. =, 24. > 7 1530
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1TSXLmgEMfkC
Ćwiczenie 19
Tosia, Zosia i Marysia czytały "Anię z Zielonego Wzgórza". Tosia przeczytała 1118 tej książki, Zosia przeczytała tyle, że została jej jeszcze 13. Marysia przeczytała 56 tej książki.
Wskaż wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Zosia przeczytała 1218 książki., 2. Zosia przeczytała 618 książki., 3. Tosia przeczytała więcej niż Marysia., 4. Marysia przeczytała najwięcej.

  • Zosia przeczytała 1218 książki.
  • Zosia przeczytała 618 książki.
  • Tosia przeczytała więcej niż Marysia.
  • Marysia przeczytała najwięcej.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R17xwe5WCgszl1
Ćwiczenie 20
Mama Basi usmażyła na śniadanie dwa jednakowe omlety. Basia zjadła 58 omleta i resztę oddała mamie, a Krysia zjadła 59 swego omleta i resztę oddała tacie. Kto zjadł większą część omleta: mama czy tata? Uzupełnij odpowiedź, przeciągając w lukę odpowiednie słowa.
Odpowiedź: Mama zjadła 1. tyle samo co, 2. więcej niż, 3. mniej niż tata.

Mama Basi usmażyła na śniadanie dwa jednakowe omlety. Basia zjadła 58 omleta i resztę oddała mamie, a Krysia zjadła 59 swego omleta i resztę oddała tacie. Kto zjadł większą część omleta: mama czy tata?

więcej, mniej, tyle samo

Mama zjadła .................. niż tata.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RL4mlOxzKXc1d
Ćwiczenie 21
Nie sprowadzając ułamków do wspólnego licznika ani do wspólnego mianownika, uzupełnij nierówności, przeciągając w luki odpowiednie znaki lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 3 231. >, 2. =, 3. >, 4. >, 5. <, 6. >, 7. =, 8. =, 9. <, 10. <, 11. <, 12. = 3 143 12 15161. >, 2. =, 3. >, 4. >, 5. <, 6. >, 7. =, 8. =, 9. <, 10. <, 11. <, 12. = 12 215 9 7101. >, 2. =, 3. >, 4. >, 5. <, 6. >, 7. =, 8. =, 9. <, 10. <, 11. <, 12. = 9 2281 4 591201. >, 2. =, 3. >, 4. >, 5. <, 6. >, 7. =, 8. =, 9. <, 10. <, 11. <, 12. = 4 3160
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Rf13ToHHTpB1P1
Ćwiczenie 22
Basia i Krysia dostały od rodziców po tyle samo pieniędzy na swoje wydatki. Basia wydała 29 otrzymanej kwoty, a Krysia wydała tyle, że zostało jej 49 z pieniędzy od rodziców. Która z dziewczynek wydała więcej pieniędzy? Której z nich zostało więcej pieniędzy? Więcej pieniędzy zostało 1. Basia, 2. Krysi, 3. Krysia, 4. Basi. Więcej pieniędzy wydała 1. Basia, 2. Krysi, 3. Krysia, 4. Basi.

Basia i Krysia dostały od rodziców po tyle samo pieniędzy na swoje wydatki. Basia wydała 29 otrzymanej kwoty, a Krysia wydała tyle, że zostało jej 49 z pieniędzy od rodziców. Która z dziewczynek wydała więcej pieniędzy? Której z nich zostało więcej pieniędzy?

Basi, Krysi, Basia, Krysia

Więcej pieniędzy zostało ............. Więcej pieniędzy wydała .............

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 23

Pola zamalowane jednym kolorem zajmują razem pewną część poziomego pasa, którą można opisać za pomocą ułamka. Jaka część jednego pasa byłaby zamalowana na pomarańczowo, gdyby wszystkie pomarańczowe części umieścić w tym pasie? I podobnie – jaka część byłaby zamalowana na zielono? Która z tych części byłaby większa?

RFePINT0vocrK1
Prostokąt złożony z sześciu pasów (małych prostokątów), każdy długości 1. Pierwszy pas nie jest podzielony na części, nie jest zamalowany. Drugi pas podzielony na dwie równe części, jedna część równa jedna druga. Trzeci pas podzielony na cztery równe części z zamalowaną na pomarańczowo jedną częścią, jedna część równa jedna czwarta. Czwarty pas podzielony na osiem równych części z zamalowanymi dwoma częściami na pomarańczowo i jedną częścią na zielono, jedna część równa jedna ósma. Piąty pas podzielony na szesnaście równych części z zamalowaną jedną częścią na pomarańczowo i czterema częściami na zielono, jedna część równa jedna szesnasta. Szósty pas podzielony na trzydzieści dwie równe części z zamalowaną jedną częścią na pomarańczowo i czterema częściami na zielono.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1aKJ5a0dsAz8
Uzupełnij zdania, przeciągając w luki odpowiednie liczby i słowa lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Gdyby wszystkie pomarańczowe części umieścić w jednym pasie, to 1. 1732, 2. 2132, 3. pomarańczowo, 4. 1532, 5. zielono, 6. 1932, 7. 1332 tego pasa byłoby zamalowane na pomarańczowo. Gdyby wszystkie zielone części umieścić w jednym pasie, to 1. 1732, 2. 2132, 3. pomarańczowo, 4. 1532, 5. zielono, 6. 1932, 7. 1332 tego pasa byłoby zamalowane na zielono. Większa część pojedynczego pasa byłaby zamalowana na 1. 1732, 2. 2132, 3. pomarańczowo, 4. 1532, 5. zielono, 6. 1932, 7. 1332.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 24

RteruhzxxFFWv
Uzupełnij poniższą nierówność, przeciągając w luki odpowiednie ułamki. 1. 37, 2. 38, 3. 47<1. 37, 2. 38, 3. 47<1. 37, 2. 38, 3. 47
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1MFyncf0UUbL1
Ćwiczenie 25
Uporządkuj elementy w kolejności rosnącej. Elementy do uszeregowania: 1. 45, 2. 49, 3. 65

Uporządkuj elementy w kolejności rosnącej.

  • 49
  • 45
  • 65
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 26

W miejsce kropek wpisz odpowiednie liczby.

  1. 37<…7<56

  2. 59<……<78

  3. 38<…8<4…

  4. …10<510<5…

  5. …11<611<6…

  6. …12<712<……

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

RRp3SZ8wbEwiA
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
5. Roszerzanie oraz skracanie ułamków
7. Ułamki zwykłe - podsumowanie