RXt1Fze9RkVC7
Na zdjęciu jest blat z lezącym kalkulatorem. Na wyświetlaczu kalkulatora jest liczba: 26,6666667. W poprzek zdjęcia na czarnym tle napis: Nie wszystko jest całością - ułamki dziesiętne

Nie wszystko jest całością - ułamki dziesiętne

Źródło: Polina Tankilevitch, domena publiczna. https://www.pexels.com/pl-pl.

1. Ułamki o mianownikach 10, 100, 1000,...

R9lPY5l1vpd2d
Kalifornijski znacznik milowy na mili 144,44.
Kalifornijski znacznik milowy na mili 144,44
Źródło: California Department of Transportation (Caltrans), domena publiczna.

Jeszcze w latach sześćdziesiątych dwudziestego wieku  na znakach  stojących  wzdłuż dróg Kalifornii (USA),  odległości wyrażone  za pomocą ułamków dziesiętnych  zapisywane były z częścią ułamkową w indeksie górnym.

R1XMARISYLbab
Portret szesnastowiecznego arystokraty Johna Napiera - mężczyzny z brodą, w średnim wieku siedzącego na krześle.
Portret Johna Napiera
Źródło: dostępny w internecie Wikimedia Commons, domena publiczna.

Szesnastowieczny szkocki arystokrata, matematyk John Napier jako pierwszy zapoczątkował współczesny zapis ułamków dziesiętnych, stosując kropkę do oddzielenia części całkowitej od ułamkowej.

Obecnie kropkę w ułamkach dziesiętnych wykorzystuje się nadal w krajach anglosaskich. W Polsce – stosujemy przecinek dziesiętny (separator dziesiętny).

Jakie liczby nazywamy ułamkami dziesiętnymi, jak się je zapisuje i odczytuje - dowiesz się, analizując poniższy materiał.

Pojęcie ułamka dziesiętnego

Wśród  ułamków zwykłych są takie, których mianowniki są równe 10, 100, 1000,...

Na przykład:

3 10 ,     26 100 ,     1 1000 ,     456 10 ,     34567 10000

Takie ułamki nazywamy ułamkami dziesiętnymi.

Ułamek dziesiętny
Definicja: Ułamek dziesiętny

Ułamek, którego mianownik jest jedną z liczb:  10, 100, 1000, … nazywamy ułamkiem dziesiętnym.

R1djchdLMocEm
Ćwiczenie 1
Zaznacz wszystkie ułamki dziesiętne. 4100 1310 102100 551000 1011 25110 60101 10015
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Przykład 1

Ułamek dziesiętny cztery setne można zapisać dwoma sposobami:

  • jako ułamek zwykły 4100

  • z wykorzystaniem przecinka, czyli w postaci dziesiętnej 0,04

Z ułamka 1310 można wyłączyć całości i otrzymamy jeden i trzy dziesiąte. 
Liczbę jeden i trzy dziesiąte zapisujemy w postaci liczby mieszanej 1310 lub z wykorzystaniem przecinka 1,3.

  • 102100=12100=1,02 czytamy: jeden i dwie setne

  • 551000=0,055 czytamy: pięćdziesiąt pięć tysięcznych

RNDs3AMWFPePY1
Ćwiczenie 2
Przedstaw ułamek zwykły w postaci dziesiętnej. Uzupełnij równości, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 710= 1. 0,62, 2. 0,034, 3. 0,0002, 4. 0,03, 5. 0,003, 6. 0,5, 7. 0,00002, 8. 0,34, 9. 0,062, 10. 0,07, 11. 0,7, 12. 0,005, 13. 0,899, 14. 0,0899, 15. 0,0001, 16. 0,001510= 1. 0,62, 2. 0,034, 3. 0,0002, 4. 0,03, 5. 0,003, 6. 0,5, 7. 0,00002, 8. 0,34, 9. 0,062, 10. 0,07, 11. 0,7, 12. 0,005, 13. 0,899, 14. 0,0899, 15. 0,0001, 16. 0,0013100= 1. 0,62, 2. 0,034, 3. 0,0002, 4. 0,03, 5. 0,003, 6. 0,5, 7. 0,00002, 8. 0,34, 9. 0,062, 10. 0,07, 11. 0,7, 12. 0,005, 13. 0,899, 14. 0,0899, 15. 0,0001, 16. 0,00162100= 1. 0,62, 2. 0,034, 3. 0,0002, 4. 0,03, 5. 0,003, 6. 0,5, 7. 0,00002, 8. 0,34, 9. 0,062, 10. 0,07, 11. 0,7, 12. 0,005, 13. 0,899, 14. 0,0899, 15. 0,0001, 16. 0,00111000= 1. 0,62, 2. 0,034, 3. 0,0002, 4. 0,03, 5. 0,003, 6. 0,5, 7. 0,00002, 8. 0,34, 9. 0,062, 10. 0,07, 11. 0,7, 12. 0,005, 13. 0,899, 14. 0,0899, 15. 0,0001, 16. 0,001341000= 1. 0,62, 2. 0,034, 3. 0,0002, 4. 0,03, 5. 0,003, 6. 0,5, 7. 0,00002, 8. 0,34, 9. 0,062, 10. 0,07, 11. 0,7, 12. 0,005, 13. 0,899, 14. 0,0899, 15. 0,0001, 16. 0,0018991000= 1. 0,62, 2. 0,034, 3. 0,0002, 4. 0,03, 5. 0,003, 6. 0,5, 7. 0,00002, 8. 0,34, 9. 0,062, 10. 0,07, 11. 0,7, 12. 0,005, 13. 0,899, 14. 0,0899, 15. 0,0001, 16. 0,001210000= 1. 0,62, 2. 0,034, 3. 0,0002, 4. 0,03, 5. 0,003, 6. 0,5, 7. 0,00002, 8. 0,34, 9. 0,062, 10. 0,07, 11. 0,7, 12. 0,005, 13. 0,899, 14. 0,0899, 15. 0,0001, 16. 0,001

Przedstaw ułamek zwykły w postaci dziesiętnej.

0,005, 0,001, 0,7, 0,003, 0,899, 0,07, 0,00002, 0,034, 0,62, 0,34, 0,0899, 0,5, 0,062, 0,0002, 0,03, 0,0001

a) 710= ..............
b) 510= ..............
c) 3100= ..............
d) 62100= ..............
e) 11 000= ..............
f) 341 000= ..............
g) 8991 000= ..............
h) 210 000= ..............

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RjUO1yUtkwf0V1
Ćwiczenie 3
Przedstaw liczbę mieszaną w postaci dziesiętnej. Uzupełnij równości, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 1310= 1. 7,015, 2. 25,306, 3. 5,008, 4. 25,3006, 5. 1,3, 6. 7,0015, 7. 5,08, 8. 2,17, 9. 10,046, 10. 8,005, 11. 3,09, 12. 8,00005, 13. 10,0046, 14. 3,9, 15. 21,7, 16. 1,033910= 1. 7,015, 2. 25,306, 3. 5,008, 4. 25,3006, 5. 1,3, 6. 7,0015, 7. 5,08, 8. 2,17, 9. 10,046, 10. 8,005, 11. 3,09, 12. 8,00005, 13. 10,0046, 14. 3,9, 15. 21,7, 16. 1,03217100= 1. 7,015, 2. 25,306, 3. 5,008, 4. 25,3006, 5. 1,3, 6. 7,0015, 7. 5,08, 8. 2,17, 9. 10,046, 10. 8,005, 11. 3,09, 12. 8,00005, 13. 10,0046, 14. 3,9, 15. 21,7, 16. 1,0358100= 1. 7,015, 2. 25,306, 3. 5,008, 4. 25,3006, 5. 1,3, 6. 7,0015, 7. 5,08, 8. 2,17, 9. 10,046, 10. 8,005, 11. 3,09, 12. 8,00005, 13. 10,0046, 14. 3,9, 15. 21,7, 16. 1,0310461000= 1. 7,015, 2. 25,306, 3. 5,008, 4. 25,3006, 5. 1,3, 6. 7,0015, 7. 5,08, 8. 2,17, 9. 10,046, 10. 8,005, 11. 3,09, 12. 8,00005, 13. 10,0046, 14. 3,9, 15. 21,7, 16. 1,03851000= 1. 7,015, 2. 25,306, 3. 5,008, 4. 25,3006, 5. 1,3, 6. 7,0015, 7. 5,08, 8. 2,17, 9. 10,046, 10. 8,005, 11. 3,09, 12. 8,00005, 13. 10,0046, 14. 3,9, 15. 21,7, 16. 1,03253061000= 1. 7,015, 2. 25,306, 3. 5,008, 4. 25,3006, 5. 1,3, 6. 7,0015, 7. 5,08, 8. 2,17, 9. 10,046, 10. 8,005, 11. 3,09, 12. 8,00005, 13. 10,0046, 14. 3,9, 15. 21,7, 16. 1,0371510000= 1. 7,015, 2. 25,306, 3. 5,008, 4. 25,3006, 5. 1,3, 6. 7,0015, 7. 5,08, 8. 2,17, 9. 10,046, 10. 8,005, 11. 3,09, 12. 8,00005, 13. 10,0046, 14. 3,9, 15. 21,7, 16. 1,03

Przedstaw liczbę mieszaną w postaci dziesiętnej.

8,00005, 5,008, 8,005, 10,046, 1,03, 1,3, 2,17, 3,9, 7,015, 5,08, 10,0046, 25,306, 3,09, 25,3006, 7,0015, 21,7

a) 1310= ..............
b) 3910= ..............
c) 217100= ..............
d) 58100= ..............
e) 10461 000= ..............
f) 851 000= ..............
g) 253061 000= ..............
h) 71510 000= ..............

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ważne!

Ułamki dziesiętne można zapisać w postaci liczb dziesiętnych, czyli liczb z przecinkiem.

  • 710=0,7, 3610=3610=3,6

  • 23100=0,23, 50131000=5131000=5,013

Mówimy też, że te ułamki lub liczby mieszane zapisane są w postaci dziesiętnej.

R1PC8wimrUFyI
Ćwiczenie 4
Połącz w pary 2100 Możliwe odpowiedzi: 1. 4,006, 2. 9,036, 3. 7,9, 4. 0,7, 5. 7,09, 6. 0,02, 7. 0,06, 8. 4,02, 9. 9,19, 10. 0,19 461000 Możliwe odpowiedzi: 1. 4,006, 2. 9,036, 3. 7,9, 4. 0,7, 5. 7,09, 6. 0,02, 7. 0,06, 8. 4,02, 9. 9,19, 10. 0,19 42100 Możliwe odpowiedzi: 1. 4,006, 2. 9,036, 3. 7,9, 4. 0,7, 5. 7,09, 6. 0,02, 7. 0,06, 8. 4,02, 9. 9,19, 10. 0,19 6100 Możliwe odpowiedzi: 1. 4,006, 2. 9,036, 3. 7,9, 4. 0,7, 5. 7,09, 6. 0,02, 7. 0,06, 8. 4,02, 9. 9,19, 10. 0,19 710 Możliwe odpowiedzi: 1. 4,006, 2. 9,036, 3. 7,9, 4. 0,7, 5. 7,09, 6. 0,02, 7. 0,06, 8. 4,02, 9. 9,19, 10. 0,19 7910 Możliwe odpowiedzi: 1. 4,006, 2. 9,036, 3. 7,9, 4. 0,7, 5. 7,09, 6. 0,02, 7. 0,06, 8. 4,02, 9. 9,19, 10. 0,19 19100 Możliwe odpowiedzi: 1. 4,006, 2. 9,036, 3. 7,9, 4. 0,7, 5. 7,09, 6. 0,02, 7. 0,06, 8. 4,02, 9. 9,19, 10. 0,19 9361000 Możliwe odpowiedzi: 1. 4,006, 2. 9,036, 3. 7,9, 4. 0,7, 5. 7,09, 6. 0,02, 7. 0,06, 8. 4,02, 9. 9,19, 10. 0,19 79100 Możliwe odpowiedzi: 1. 4,006, 2. 9,036, 3. 7,9, 4. 0,7, 5. 7,09, 6. 0,02, 7. 0,06, 8. 4,02, 9. 9,19, 10. 0,19 919100 Możliwe odpowiedzi: 1. 4,006, 2. 9,036, 3. 7,9, 4. 0,7, 5. 7,09, 6. 0,02, 7. 0,06, 8. 4,02, 9. 9,19, 10. 0,19
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 5

Odczytaj, jaką część kwadratu zamalowano.

Rvox4qoyxgX3o
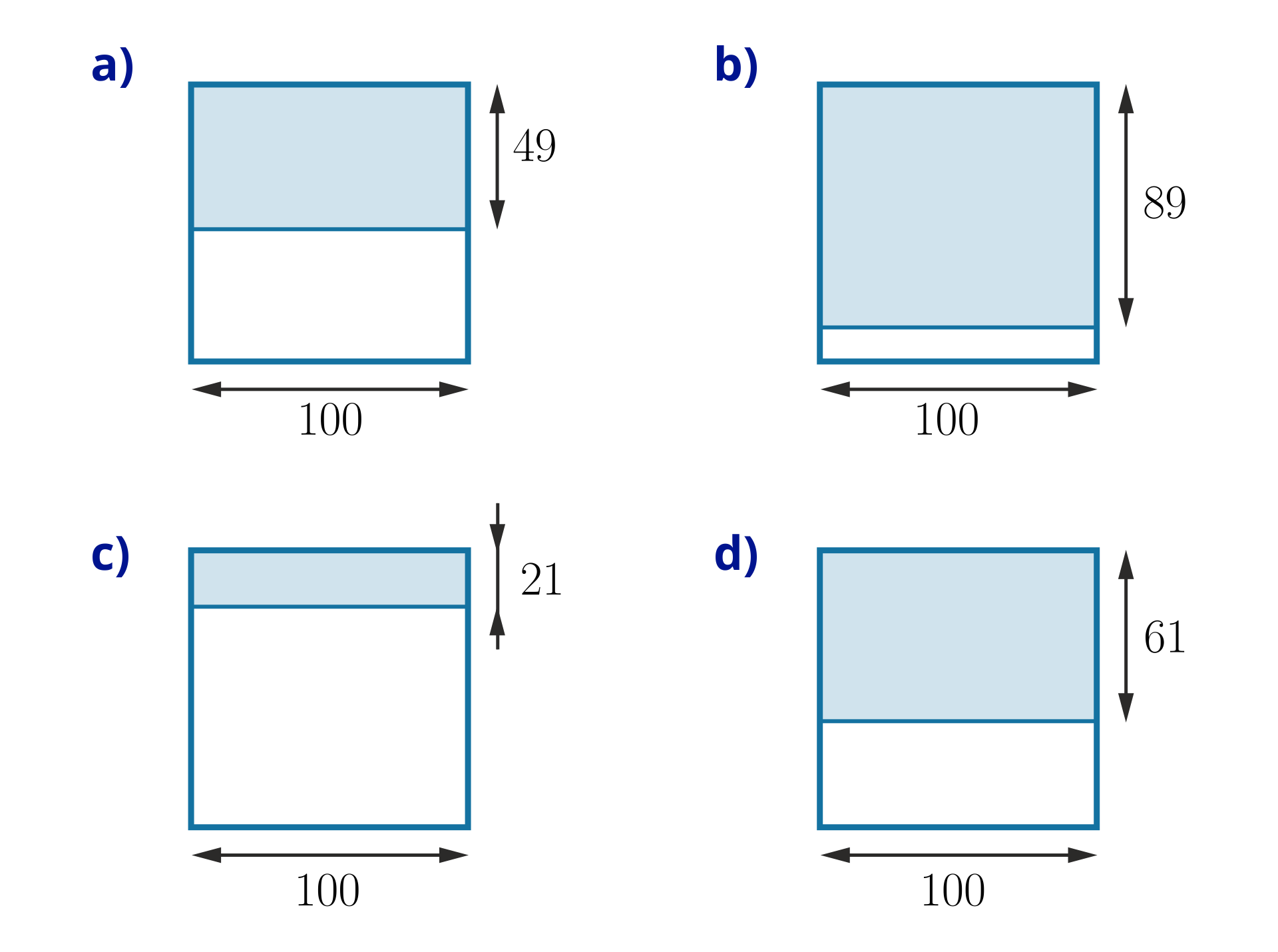
Ilustracja przedstawia cztery kwadraty o boku długości 100, każdy kwadrat ma zacieniowany pewny fragment. W kwadracie A zacieniowany jest fragment szerokości całego kwadratu i wysokości 49, a kwadracie B zacieniowany jest fragment szerokości całego kwadratu i wysokości 89, w kwadracie C zacieniowany jest fragment szerokości całego kwadratu i wysokości 21, w kwadracie D zacieniowany jest fragment szerokości całego kwadratu i wysokości sześćdziesiąt jeden.
Źródło: GroMar, licencja: CC BY 3.0.
R8IqFHlFFxISR
Uzupełnij poniższe zdania odpowiednimi liczbami. Kliknij w lukę, aby rozwinąć listę i wybierz odpowiednie liczby w każdym zdaniu. W kwadracie A zamalowana część stanowi 1. 4,9, 2. 2,1, 3. 0,89, 4. 0,021, 5. 0,089, 6. 0,61, 7. 0,49, 8. 6,1, 9. 8,9, 10. 0,21, 11. 0,061 całej figury.W kwadracie B zamalowana część stanowi 1. 4,9, 2. 2,1, 3. 0,89, 4. 0,021, 5. 0,089, 6. 0,61, 7. 0,49, 8. 6,1, 9. 8,9, 10. 0,21, 11. 0,061 całej figury.W kwadracie C zamalowana część stanowi 1. 4,9, 2. 2,1, 3. 0,89, 4. 0,021, 5. 0,089, 6. 0,61, 7. 0,49, 8. 6,1, 9. 8,9, 10. 0,21, 11. 0,061 całej figury.W kwadracie D zamalowana część stanowi 1. 4,9, 2. 2,1, 3. 0,89, 4. 0,021, 5. 0,089, 6. 0,61, 7. 0,49, 8. 6,1, 9. 8,9, 10. 0,21, 11. 0,061 całej figury.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1IQBx8HCFDPs
Ćwiczenie 6
25100 Możliwe odpowiedzi: 1. 1,04, 2. 5,2, 3. 1,4, 4. 0,025, 5. 1,004, 6. 2,5, 7. 1,40, 8. 0,25, 9. 1,040, 10. 0,0025, 11. 1,400, 12. 0,52 2510 Możliwe odpowiedzi: 1. 1,04, 2. 5,2, 3. 1,4, 4. 0,025, 5. 1,004, 6. 2,5, 7. 1,40, 8. 0,25, 9. 1,040, 10. 0,0025, 11. 1,400, 12. 0,52 251000 Możliwe odpowiedzi: 1. 1,04, 2. 5,2, 3. 1,4, 4. 0,025, 5. 1,004, 6. 2,5, 7. 1,40, 8. 0,25, 9. 1,040, 10. 0,0025, 11. 1,400, 12. 0,52 2510000 Możliwe odpowiedzi: 1. 1,04, 2. 5,2, 3. 1,4, 4. 0,025, 5. 1,004, 6. 2,5, 7. 1,40, 8. 0,25, 9. 1,040, 10. 0,0025, 11. 1,400, 12. 0,52 52100 Możliwe odpowiedzi: 1. 1,04, 2. 5,2, 3. 1,4, 4. 0,025, 5. 1,004, 6. 2,5, 7. 1,40, 8. 0,25, 9. 1,040, 10. 0,0025, 11. 1,400, 12. 0,52 5210 Możliwe odpowiedzi: 1. 1,04, 2. 5,2, 3. 1,4, 4. 0,025, 5. 1,004, 6. 2,5, 7. 1,40, 8. 0,25, 9. 1,040, 10. 0,0025, 11. 1,400, 12. 0,52 1410 Możliwe odpowiedzi: 1. 1,04, 2. 5,2, 3. 1,4, 4. 0,025, 5. 1,004, 6. 2,5, 7. 1,40, 8. 0,25, 9. 1,040, 10. 0,0025, 11. 1,400, 12. 0,52 14100 Możliwe odpowiedzi: 1. 1,04, 2. 5,2, 3. 1,4, 4. 0,025, 5. 1,004, 6. 2,5, 7. 1,40, 8. 0,25, 9. 1,040, 10. 0,0025, 11. 1,400, 12. 0,52 141000 Możliwe odpowiedzi: 1. 1,04, 2. 5,2, 3. 1,4, 4. 0,025, 5. 1,004, 6. 2,5, 7. 1,40, 8. 0,25, 9. 1,040, 10. 0,0025, 11. 1,400, 12. 0,52 1401000 Możliwe odpowiedzi: 1. 1,04, 2. 5,2, 3. 1,4, 4. 0,025, 5. 1,004, 6. 2,5, 7. 1,40, 8. 0,25, 9. 1,040, 10. 0,0025, 11. 1,400, 12. 0,52 140100 Możliwe odpowiedzi: 1. 1,04, 2. 5,2, 3. 1,4, 4. 0,025, 5. 1,004, 6. 2,5, 7. 1,40, 8. 0,25, 9. 1,040, 10. 0,0025, 11. 1,400, 12. 0,52 14001000 Możliwe odpowiedzi: 1. 1,04, 2. 5,2, 3. 1,4, 4. 0,025, 5. 1,004, 6. 2,5, 7. 1,40, 8. 0,25, 9. 1,040, 10. 0,0025, 11. 1,400, 12. 0,52
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zamiana liczb dziesiętnych na ułamki zwykłe

Przykład 2

Liczby dziesiętne możemy zapisać w postaci ułamka zwykłego lub liczby mieszanej. Jeżeli można, skracamy otrzymany ułamek zwykły.

  • 0,9=910

  • 2,3=2310

  • 0,5=510=12

  • 4,6=4610=435

  • 0,25=25100=14

  • 7,042=7421000=721500

Zauważ, że 0,5 to połowa, a 0,25 to ćwierć całości.

R1doZUpAwHGLY1
Ćwiczenie 7
Połącz w pary elementy tak, aby liczbom w postaci dziesiętnej odpowiadały ułamki i liczby mieszane . 0,9 Możliwe odpowiedzi: 1. 14, 2. 610, 3. 910, 4. 12, 5. 235, 6. 20100, 7. 721500, 8. 6131000, 9. 4610, 10. 2310 2,3 Możliwe odpowiedzi: 1. 14, 2. 610, 3. 910, 4. 12, 5. 235, 6. 20100, 7. 721500, 8. 6131000, 9. 4610, 10. 2310 0,6 Możliwe odpowiedzi: 1. 14, 2. 610, 3. 910, 4. 12, 5. 235, 6. 20100, 7. 721500, 8. 6131000, 9. 4610, 10. 2310 4,6 Możliwe odpowiedzi: 1. 14, 2. 610, 3. 910, 4. 12, 5. 235, 6. 20100, 7. 721500, 8. 6131000, 9. 4610, 10. 2310 0,2 Możliwe odpowiedzi: 1. 14, 2. 610, 3. 910, 4. 12, 5. 235, 6. 20100, 7. 721500, 8. 6131000, 9. 4610, 10. 2310 6,013 Możliwe odpowiedzi: 1. 14, 2. 610, 3. 910, 4. 12, 5. 235, 6. 20100, 7. 721500, 8. 6131000, 9. 4610, 10. 2310 0,5 Możliwe odpowiedzi: 1. 14, 2. 610, 3. 910, 4. 12, 5. 235, 6. 20100, 7. 721500, 8. 6131000, 9. 4610, 10. 2310 2,6 Możliwe odpowiedzi: 1. 14, 2. 610, 3. 910, 4. 12, 5. 235, 6. 20100, 7. 721500, 8. 6131000, 9. 4610, 10. 2310 0,25 Możliwe odpowiedzi: 1. 14, 2. 610, 3. 910, 4. 12, 5. 235, 6. 20100, 7. 721500, 8. 6131000, 9. 4610, 10. 2310 7,042 Możliwe odpowiedzi: 1. 14, 2. 610, 3. 910, 4. 12, 5. 235, 6. 20100, 7. 721500, 8. 6131000, 9. 4610, 10. 2310

Połącz w pary.

<span aria-label="siedem początek ułamka, dwadzieścia jeden, mianownik, pięćset, koniec ułamka" role="math"><math><mstyle mathsize="20px"><mn>7</mn><mfrac><mn>21</mn><mn>500</mn></mfrac></mstyle></math></span>, <span aria-label="początek ułamka, jeden, mianownik, cztery, koniec ułamka" role="math"><math><mstyle mathsize="20px"><mfrac><mn>1</mn><mn>4</mn></mfrac></mstyle></math></span>, <span aria-label="początek ułamka, jeden, mianownik, dwa, koniec ułamka" role="math"><math><mstyle mathsize="20px"><mfrac><mn>1</mn><mn>2</mn></mfrac></mstyle></math></span>, <span aria-label="dwa początek ułamka, trzy, mianownik, pięć, koniec ułamka" role="math"><math><mstyle mathsize="20px"><mn>2</mn><mfrac><mn>3</mn><mn>5</mn></mfrac></mstyle></math></span>, <span aria-label="cztery początek ułamka, sześć, mianownik, dziesięć, koniec ułamka" role="math"><math><mstyle mathsize="20px"><mn>4</mn><mfrac><mn>6</mn><mn>10</mn></mfrac></mstyle></math></span>, <span aria-label="początek ułamka, dziewięć, mianownik, dziesięć, koniec ułamka" role="math"><math><mstyle mathsize="20px"><mfrac><mn>9</mn><mn>10</mn></mfrac></mstyle></math></span>, <span aria-label="dwa początek ułamka, trzy, mianownik, dziesięć, koniec ułamka" role="math"><math><mstyle mathsize="20px"><mn>2</mn><mfrac><mn>3</mn><mn>10</mn></mfrac></mstyle></math></span>, <span aria-label="sześć początek ułamka, trzynaście, mianownik, tysiąc, koniec ułamka" role="math"><math><mstyle mathsize="20px"><mn>6</mn><mfrac><mn>13</mn><mn>1000</mn></mfrac></mstyle></math></span>, <span aria-label="początek ułamka, dwadzieścia, mianownik, sto, koniec ułamka" role="math"><math><mstyle mathsize="20px"><mfrac><mn>20</mn><mn>100</mn></mfrac></mstyle></math></span>, <span aria-label="początek ułamka, sześć, mianownik, dziesięć, koniec ułamka" role="math"><math><mstyle mathsize="20px"><mfrac><mn>6</mn><mn>10</mn></mfrac></mstyle></math></span>

0,9  
2,3  
0,6  
4,6  
0,2  
6,013  
0,5  
2,6  
0,25  
7,042  
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R12n2bbIm16tk
Ćwiczenie 8
Przekształć liczby dziesiętne w postać nieskracalnych ułamków zwykłych
Połącz w pary działanie z wynikiem. 0,2 Możliwe odpowiedzi: 1. 15, 2. 320, 3. 25, 4. 12, 5. 34, 6. 14 0,4 Możliwe odpowiedzi: 1. 15, 2. 320, 3. 25, 4. 12, 5. 34, 6. 14 0,15 Możliwe odpowiedzi: 1. 15, 2. 320, 3. 25, 4. 12, 5. 34, 6. 14 0,25 Możliwe odpowiedzi: 1. 15, 2. 320, 3. 25, 4. 12, 5. 34, 6. 14 0,5 Możliwe odpowiedzi: 1. 15, 2. 320, 3. 25, 4. 12, 5. 34, 6. 14 0,75 Możliwe odpowiedzi: 1. 15, 2. 320, 3. 25, 4. 12, 5. 34, 6. 14
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R16pshTHWD0lN
Ćwiczenie 9
Przekształć liczby dziesiętne w postać nieskracalnych ułamków zwykłych lub licz mieszanych.
Połącz w pary działanie z wynikiem. 0,36 Możliwe odpowiedzi: 1. 114, 2. 925, 3. 2425, 4. 538, 5. 5111250, 6. 41125 1,25 Możliwe odpowiedzi: 1. 114, 2. 925, 3. 2425, 4. 538, 5. 5111250, 6. 41125 2,16 Możliwe odpowiedzi: 1. 114, 2. 925, 3. 2425, 4. 538, 5. 5111250, 6. 41125 5,444 Możliwe odpowiedzi: 1. 114, 2. 925, 3. 2425, 4. 538, 5. 5111250, 6. 41125 4,008 Możliwe odpowiedzi: 1. 114, 2. 925, 3. 2425, 4. 538, 5. 5111250, 6. 41125 5,375 Możliwe odpowiedzi: 1. 114, 2. 925, 3. 2425, 4. 538, 5. 5111250, 6. 41125
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ru14BR8xBip40
Ćwiczenie 10
Liczbę dziesiętną przedstaw w postaci liczby mieszanej, ze skróconym ułamkiem. Uzupełnij równości, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 13,2= 1. 511200, 2. 301225, 3. 9320, 4. 301220, 5. 1315, 6. 1115, 7. 9315, 8. 1215, 9. 251220, 10. 611100, 11. 8315, 12. 5111009,15= 1. 511200, 2. 301225, 3. 9320, 4. 301220, 5. 1315, 6. 1115, 7. 9315, 8. 1215, 9. 251220, 10. 611100, 11. 8315, 12. 51110030,48= 1. 511200, 2. 301225, 3. 9320, 4. 301220, 5. 1315, 6. 1115, 7. 9315, 8. 1215, 9. 251220, 10. 611100, 11. 8315, 12. 5111005,055= 1. 511200, 2. 301225, 3. 9320, 4. 301220, 5. 1315, 6. 1115, 7. 9315, 8. 1215, 9. 251220, 10. 611100, 11. 8315, 12. 511100
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RzBORdtlgf17v1
Ćwiczenie 11
Uzupełnij liczniki ułamków, wpisując w luki odpowiednie liczby. Jeżeli 0,2=x110, to x1= Tu uzupełnij.Jeżeli 0,36=x2100, to x2= Tu uzupełnij.Jeżeli 0,105=x31000, to x3= Tu uzupełnij.Jeżeli 0,9999=x410000, to x4= Tu uzupełnij.

Uzupełnij liczniki ułamków.

Jeżeli 0,2=x110, to  x1= ............
Jeżeli 0,36=x2100, to  x2= ............
Jeżeli 0,105=x31000, to  x3= ............
Jeżeli 0,9999=x410000, to  x4= ............

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RKvAtCTtdgNYK1
Ćwiczenie 12
Uzupełnij mianowniki ułamków, wpisując w luki odpowiednie liczby. Jeżeli 0,234=234x1, to x1=Tu uzupełnij.Jeżeli 0,94=94x2, to x2=Tu uzupełnij.Jeżeli 0,031=31x3, to x3=Tu uzupełnij.Jeżeli 0,0099=99x4, to x4=Tu uzupełnij.

Uzupełnij mianowniki ułamków.

a) Jeżeli 0,234=234x1, to  x1= ............
b) Jeżeli 0,94=94x2, to  x2= ............
c) Jeżeli 0,031=31x3, to  x3= ............
d) Jeżeli 0,0099=99x4, to  x4= ............

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zamiana ułamków zwykłych na liczby dziesiętne

Przykład 3

Zapisywaliśmy już ułamek dziesiętny w postaci dziesiętnej. Niektóre ułamki zwykłe, chociaż nie mają mianownika 10, 100, 1000 można również zapisać w postaci dziesiętnej. Wystarczy odpowiednio rozszerzyć ułamek zwykły.

Na przykład:

  • 25=410=0,4 - rozszerzyliśmy ułamek 25 przez 2

  • 825=32100=0,32 - rozszerzyliśmy ułamek 825 przez 4

R17AGNOM4BIZ01
Ćwiczenie 13
Przez jaką liczbę należy rozszerzyć dany ułamek, żeby można go zapisać w postaci dziesiętnej? Uzupełnij zdania, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Liczbę 12 należy rozszerzyć przez 1. 25, 2. 4, 3. 2, 4. 4, 5. 4, 6. 5, 7. 5, 8. 2, 9. 5, 10. 5, 11. 4, 12. 25, 13. 25, 14. 25, 15. 5, 16. 2.Liczbę 32 należy rozszerzyć przez 1. 25, 2. 4, 3. 2, 4. 4, 5. 4, 6. 5, 7. 5, 8. 2, 9. 5, 10. 5, 11. 4, 12. 25, 13. 25, 14. 25, 15. 5, 16. 2.Liczbę 34 należy rozszerzyć przez 1. 25, 2. 4, 3. 2, 4. 4, 5. 4, 6. 5, 7. 5, 8. 2, 9. 5, 10. 5, 11. 4, 12. 25, 13. 25, 14. 25, 15. 5, 16. 2.Liczbę 725 należy rozszerzyć przez 1. 25, 2. 4, 3. 2, 4. 4, 5. 4, 6. 5, 7. 5, 8. 2, 9. 5, 10. 5, 11. 4, 12. 25, 13. 25, 14. 25, 15. 5, 16. 2.

Przez jaką liczbę należy rozszerzyć dany ułamek, żeby można go zapisać w postaci dziesiętnej? Wybierz odpowiedź.

przez 2, przez 5, przez 5, przez 25, przez 4, przez 5, przez 4, przez 2, przez 4, przez 4, przez 2, przez 5, przez 2, przez 25, przez 25, przez 25

a) 12 ................
b) 35 ................
c) 34 ................
d) 725 ................

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RoduQtGWnhbW9
Ćwiczenie 14
Łączenie par. Rozstrzygnij, czy równość jest prawdziwa, czy fałszywa. Zaznacz prawda lub fałsz w każdym wierszu tabeli.. 1 5 = 0,2 . Możliwe odpowiedzi: Prawda, Fałsz. 13 20 = 0,5 . Możliwe odpowiedzi: Prawda, Fałsz. 7 250 = 0,28 . Możliwe odpowiedzi: Prawda, Fałsz. 1 1 4 = 1,20 . Możliwe odpowiedzi: Prawda, Fałsz. 3 19 50 = 3,38 . Możliwe odpowiedzi: Prawda, Fałsz. 133 500 = 0,0266 . Możliwe odpowiedzi: Prawda, Fałsz

Rozstrzygnij, czy równość jest prawdziwa, czy fałszywa.

PRAWDA FAŁSZ
1 5 = 0,2 □ □
13 20 = 0,5 □ □
7 250 = 0,28 □ □
1 1 4 = 1,20 □ □
3 19 50 = 3,38 □ □
133 500 = 0,0266 □ □
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 15
R15vTjfeTz1At
Wśród pięciu liczb tylko jedna liczba nie jest równa pozostałym. Wyznacz tę liczbę i uzasadnij swoją odpowiedź. Uzupełnij zdania, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Spośród liczb 1825, 2430, 0,72, 3650, 72100 liczba, która ma inną wartość od pozostałych to 1. 5520, 2. 3650, 3. 21220, 4. 2610, 5. 212200, 6. 2,60, 7. 5125200, 8. 514, 9. 72100, 10. 5,25, 11. 0,72, 12. 2430, 13. 1825, 14. 5,250, 15. 235.Spośród liczb 235, 21220, 2,60, 2610, 212200 liczba, która ma inną wartość od pozostałych to 1. 5520, 2. 3650, 3. 21220, 4. 2610, 5. 212200, 6. 2,60, 7. 5125200, 8. 514, 9. 72100, 10. 5,25, 11. 0,72, 12. 2430, 13. 1825, 14. 5,250, 15. 235.Spośród liczb 5520, 514, 5,250, 5125200, 5,25 liczba, która ma inną wartość od pozostałych to 1. 5520, 2. 3650, 3. 21220, 4. 2610, 5. 212200, 6. 2,60, 7. 5125200, 8. 514, 9. 72100, 10. 5,25, 11. 0,72, 12. 2430, 13. 1825, 14. 5,250, 15. 235.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Nie wszystko jest całością - ułamki zwykłe
2. Zapisywanie i odczytywanie ułamków dziesiętnych