1. Dodawanie i odejmowanie ułamków o jednakowych mianownikach

RiXmuouIwXTLB

R7wALlZneUHOI1

Rysunek przedstawia hieroglif złożony z dwóch jednakowych łuków, kształtem przypominający usta. — Źródło: domena publiczna. https://www.iconfinder.com/.

Zasady działań na ułamkach zwykłych znane były już w starożytnym Egipcie. Hieroglif oznaczający ułamek wyglądał jak „usta” i oznaczał „część”. Umieszczano go nad liczbą. Na przykład umieszczenie tego znaku nad liczbą trzy oznaczało ułamek $\frac{1}{3}$ .

Analizując przykłady zawarte w tym materiale poznasz sposoby dodawania oraz odejmowania ułamków o jednakowych mianownikach. Dowiesz się też, jak dodawać i odejmować liczby mieszane. Rozwiązując ćwiczenia – sprawdzisz nabyte umiejętności.

Dodawanie i odejmowanie ułamków

Przykład 1

Spójrzmy na rysunek i obliczmy, jaka część figury została zamalowana.

RtrcrnGCXFPpy1

Rysunek trójkąta podzielonego na 16 równych części. Na zielono zamalowano cztery części, na niebiesko osiem z szesnastu części. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Kolorem niebieskim zamalowano $\frac{8}{16}$ trójkąta, a kolorem zielonym $\frac{5}{16}$ trójkąta.

Łącznie zamalowano więc $\frac{8}{16} + \frac{5}{16} = \frac{13}{16}$ tej figury.

Ważne!

Aby dodać ułamki o jednakowych mianownikach, należy dodać ich liczniki, a mianownik pozostawić bez zmiany.

$\frac{3}{8} + \frac{2}{8} = \frac{3 + 2}{8} = \frac{5}{8}$

$\frac{5}{17} + \frac{7}{17} = \frac{5 + 7}{17} = \frac{12}{17}$

Przeważnie dodawanie liczników wykonujemy w pamięci.

$\frac{3}{8} + \frac{2}{8} = \frac{5}{8}$

R1BglqhCRrx5S1

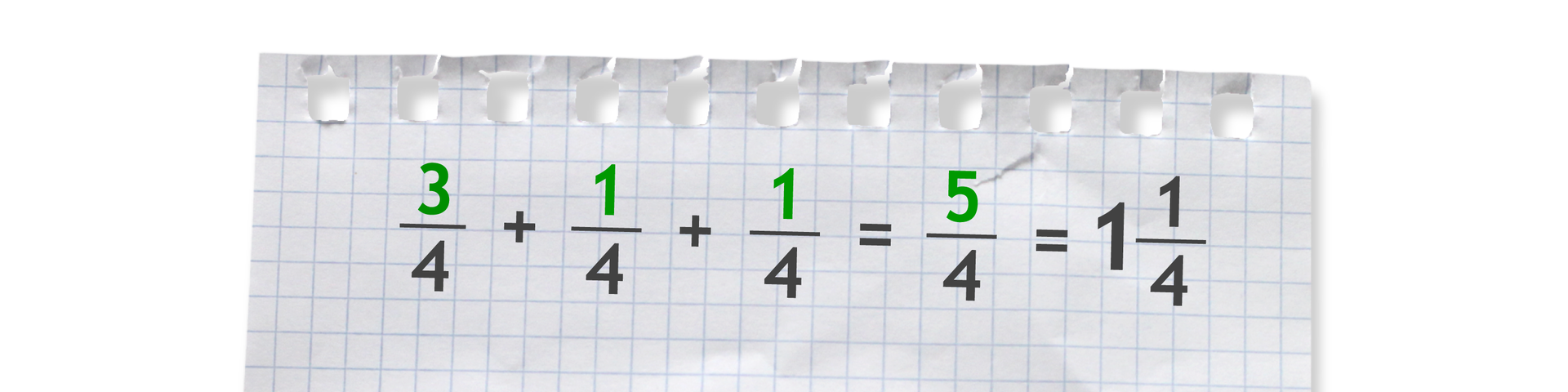
Przykład: trzy czwarte plus jedna czwarta plus jedna czwarta równa się pięć czwartych równa się jedna cała i jedna czwarta. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ważne!

Jeżeli wynik dodawania jest ułamkiem niewłaściwym, można go zapisać w postaci liczby mieszanej. Warto także skrócić część ułamkową liczby mieszanej.

Na przykład:

$\frac{7}{8} + \frac{5}{8} = \frac{12}{8} = 1 \frac{4}{8} = 1 \frac{1}{2}$

Przykład 2

Na rysunku zamalowano $\frac{9}{16}$ trójkąta. Jaka część figury nie została zamalowana?

RyDD1ZVDww6yI1

Rysunek trójkąta podzielonego na 16 równych części. Zamalowane 9 części. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Można policzyć, że nie zamalowano $\frac{7}{16}$ trójkąta.

Wynik ten możemy otrzymać tak

$1$ trójkąt $-$ $\frac{9}{16}$ trójkąta $= \frac{16}{16}$ trójkąta $- \frac{9}{16}$ trójkąta $= \frac{7}{16}$ trójkąta

Ważne!

Aby odjąć dwa ułamki o jednakowych mianownikach, należy odjąć ich liczniki, a mianownik pozostawić bez zmiany.

$\frac{3}{8} - \frac{2}{8} = \frac{3 - 2}{8} = \frac{1}{8}$

Odejmowanie liczników przeważnie wykonujemy w pamięci.

$\frac{7}{8} - \frac{2}{8} = \frac{5}{8}$

Ważne!

Jeżeli wynik odejmowania jest ułamkiem niewłaściwym, to można zapisać go w postaci liczby mieszanej. Można także skracać ułamek w liczbie mieszanej.

Na przykład:

$\frac{17}{8} - \frac{5}{8} = \frac{12}{8} = 1 \frac{4}{8} = 1 \frac{1}{2}$

Przykład 3

W przypadku, gdy od liczby całkowitej chcemy odjąć ułamek, warto liczbę całkowitą zamienić na ułamek o mianowniku takim, jak w odejmowanym ułamku.

RL8bYv7Emc73n

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ważne!

Odejmując ułamek od liczby całkowitej, możemy dla ułatwienia obliczeń zamienić tę liczbę na ułamek niewłaściwy.

RdITxjnsMYCOt1

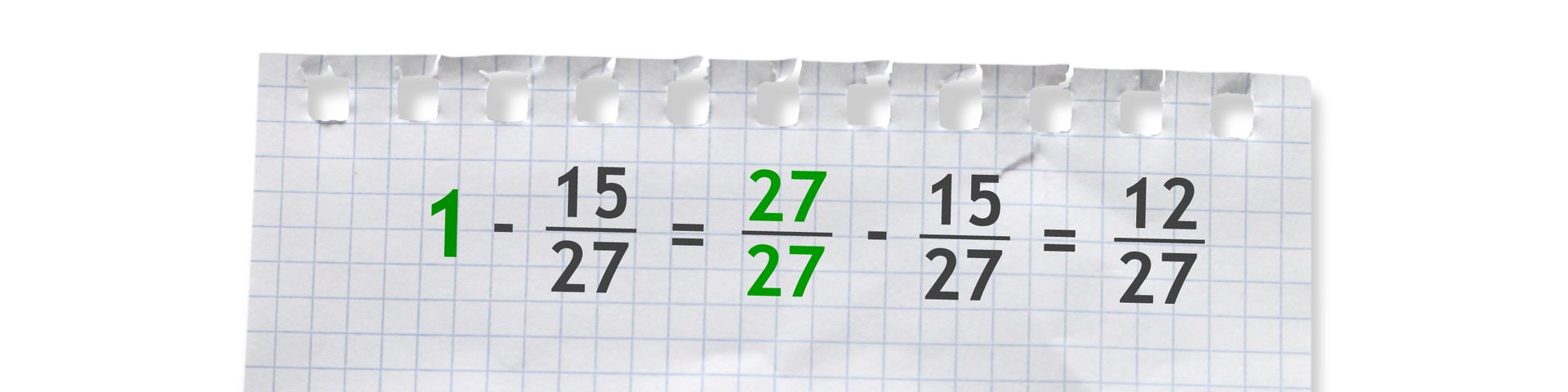
Przykład: jeden minus piętnaście dwudziestych siódmych równa się dwadzieścia siedem dwudziestych siódmych minus piętnaście dwudziestych siódmych równa się dwanaście dwudziestych siódmych. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przykład 4

Agatka zaplanowała czterodniową wycieczkę rowerową. Pierwszego dnia pokonała $\frac{2}{7}$ długości trasy, drugiego dnia $\frac{3}{7}$ , a trzeciego tylko $\frac{1}{7}$ długości trasy.

Jaką część planowanej drogi pokonała Agatka w ciągu trzech dni?

RADPtuB2scdkN1

Rysunek prostokąta podzielonego na siedem równych części. Różnymi kolorami zamalowane dwie części, trzy części i jedna część. Pod nimi odpowiednio ułamki: dwie siódme, trzy siódme i jedna siódma. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Z rysunku widać, że Agatka przejechała $\frac{6}{7}$ długości całej trasy.

Zapiszmy obliczenia.

$\frac{2}{7} + \frac{3}{7} + \frac{1}{7} = \frac{6}{7}$

Jaką część planowanej drogi musi jeszcze pokonać Agatka?

RytXRrhsexJ001

Rysunek prostokąta podzielonego na siedem równych części. Różnymi kolorami zamalowana sumę sześciu części, czyli ułamek sześć siódmych. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Z rysunku widać, że Agatka musi przejechać jeszcze $\frac{1}{7}$ długości całej trasy.

Zapiszmy obliczenia.

$1 - \frac{6}{7} = \frac{7}{7} - \frac{6}{7} = \frac{1}{7}$

Podsumujmy teraz uzyskane wiadomości.

Ważne!

Dodając (odejmując) ułamki o jednakowych mianownikach, dodajemy (odejmujemy) ich liczniki, a mianownik pozostawiamy bez zmian.

RzgMKTOI5UU1R1

Dwa przykłady. Pierwszy przykład: jedna piąta plus trzy piąte równa się cztery piąte. Drugi przykład: siedem jedenastych minus dwie jedenaste równa się pięć jedenastych. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ważne!

Jeśli w wyniku otrzymamy ułamek skracalny, warto go skrócić.

ReG0jsMsIASZj1

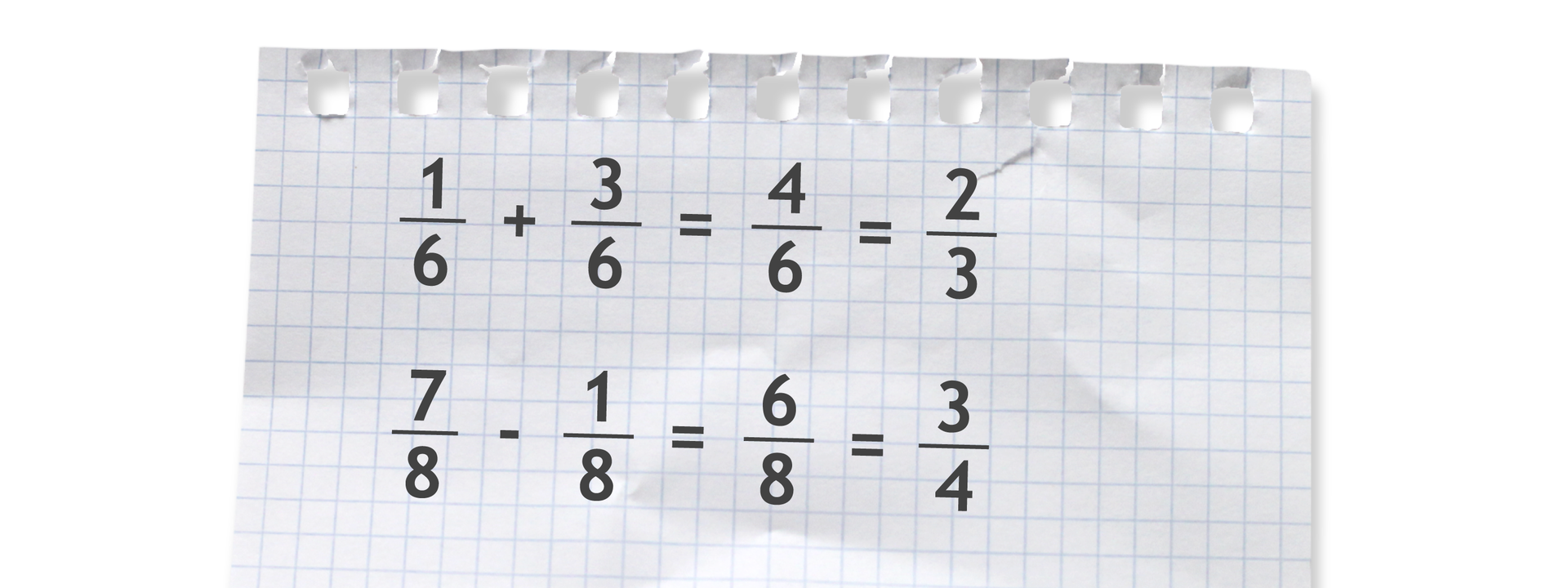
Dwa przykłady. Pierwszy: jedna szósta plus trzy szóste równa się cztery szóste równa się dwie trzecie. Drugi: siedem ósmych minus jedna ósma równa się sześć ósmych równa się trzy czwarte. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 1

Oblicz i uzupełnij zdania, wpisując jaka część figury została zamalowana. Przepisz do zeszytu i uzupełnij dodawania ułamków.

RmbYno7XFnABU1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1JEmYwNmed0o1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RAoXs2dpOE7rO1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R5qDFsdDlw55m

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 2

Zastanów się, jakie dodawanie zilustrowane jest rysunkiem, a następnie przeciągnij odpowiednie ułamki w puste pola na grafikach.

R1QvaJYWsxnfK
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RQ0T9zzBIMCuR
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1716Sl0fxLtm
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RaMTJngijZrIM

Uzupełnij zdania. Kliknij w lukę, aby rozwinąć listę, a następnie wybierz prawidłową równość. Na pierwszym rysunku znajdują się trzy paski podzielone na sześć równych części każdy. Pierwszy pasek ma zamalowane dwie części, po nim znajduje się znak plus. Drugi pasek ma zamalowane trzy części, po nim znajduje się znak równości. Ostatni pasek ma zamalowane pięć części. Ten rysunek ilustruje dodawanie 1.

\frac{5}{10} + \frac{3}{10} = \frac{8}{10}

, 2.

\frac{4}{10} + \frac{5}{10} = \frac{9}{10}

, 3.

\frac{4}{12} + \frac{5}{12} = \frac{9}{12}

, 4.

\frac{5}{9} + \frac{3}{9} = \frac{8}{9}

, 5.

\frac{4}{11} + \frac{5}{11} = \frac{9}{11}

, 6.

\frac{2}{6} + \frac{3}{6} = \frac{5}{6}

, 7.

\frac{5}{7} + \frac{3}{7} = \frac{8}{7}

, 8.

\frac{2}{4} + \frac{3}{4} = \frac{5}{4}

, 9.

\frac{2}{7} + \frac{3}{7} = \frac{5}{7}

. Na drugim rysunku znajdują się trzy paski podzielone na dziewięć równych części każdy. Pierwszy pasek ma zamalowane pięć części, po nim znajduje się znak plus. Drugi pasek ma zamalowane trzy części, po nim znajduje się znak równości. Ostatni pasek ma zamalowane osiem części. Ten rysunek ilustruje dodawanie 1.

\frac{5}{10} + \frac{3}{10} = \frac{8}{10}

, 2.

\frac{4}{10} + \frac{5}{10} = \frac{9}{10}

, 3.

\frac{4}{12} + \frac{5}{12} = \frac{9}{12}

, 4.

\frac{5}{9} + \frac{3}{9} = \frac{8}{9}

, 5.

\frac{4}{11} + \frac{5}{11} = \frac{9}{11}

, 6.

\frac{2}{6} + \frac{3}{6} = \frac{5}{6}

, 7.

\frac{5}{7} + \frac{3}{7} = \frac{8}{7}

, 8.

\frac{2}{4} + \frac{3}{4} = \frac{5}{4}

, 9.

\frac{2}{7} + \frac{3}{7} = \frac{5}{7}

. Na trzecim rysunku znajdują się trzy paski podzielone na jedenaście równych części każdy. Pierwszy pasek ma zamalowane cztery części, po nim znajduje się znak plus. Drugi pasek ma zamalowane pięć części, po nim znajduje się znak równości. Ostatni pasek ma zamalowane dziewięć części. Ten rysunek ilustruje dodawanie 1.

\frac{5}{10} + \frac{3}{10} = \frac{8}{10}

, 2.

\frac{4}{10} + \frac{5}{10} = \frac{9}{10}

, 3.

\frac{4}{12} + \frac{5}{12} = \frac{9}{12}

, 4.

\frac{5}{9} + \frac{3}{9} = \frac{8}{9}

, 5.

\frac{4}{11} + \frac{5}{11} = \frac{9}{11}

, 6.

\frac{2}{6} + \frac{3}{6} = \frac{5}{6}

, 7.

\frac{5}{7} + \frac{3}{7} = \frac{8}{7}

, 8.

\frac{2}{4} + \frac{3}{4} = \frac{5}{4}

, 9.

\frac{2}{7} + \frac{3}{7} = \frac{5}{7}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1EAmMIblGcsD

Ćwiczenie 3

Wykonaj dodawanie ułamków. Uzupełnij równości, przeciągając w luki odpowiednie liczby.

\frac{3}{8} + \frac{2}{8} =

\frac{44}{50}

, 2.

\frac{3}{5}

, 3.

\frac{5}{8}

, 4.

\frac{27}{28}

, 5.

\frac{7}{10}

, 6.

\frac{13}{14}

, 7.

\frac{28}{29}

, 8.

\frac{7}{9}

, 9.

\frac{59}{100}

, 10.

\frac{5}{7}

, 11.

\frac{69}{100}

, 12.

\frac{43}{50}

, 13.

\frac{14}{15}

, 14.

\frac{3}{4}

, 15.

\frac{15}{17}

\frac{1}{4} + \frac{2}{4} =

\frac{44}{50}

, 2.

\frac{3}{5}

, 3.

\frac{5}{8}

, 4.

\frac{27}{28}

, 5.

\frac{7}{10}

, 6.

\frac{13}{14}

, 7.

\frac{28}{29}

, 8.

\frac{7}{9}

, 9.

\frac{59}{100}

, 10.

\frac{5}{7}

, 11.

\frac{69}{100}

, 12.

\frac{43}{50}

, 13.

\frac{14}{15}

, 14.

\frac{3}{4}

, 15.

\frac{15}{17}

\frac{5}{10} + \frac{2}{10} =

\frac{44}{50}

, 2.

\frac{3}{5}

, 3.

\frac{5}{8}

, 4.

\frac{27}{28}

, 5.

\frac{7}{10}

, 6.

\frac{13}{14}

, 7.

\frac{28}{29}

, 8.

\frac{7}{9}

, 9.

\frac{59}{100}

, 10.

\frac{5}{7}

, 11.

\frac{69}{100}

, 12.

\frac{43}{50}

, 13.

\frac{14}{15}

, 14.

\frac{3}{4}

, 15.

\frac{15}{17}

\frac{9}{14} + \frac{4}{14} =

\frac{44}{50}

, 2.

\frac{3}{5}

, 3.

\frac{5}{8}

, 4.

\frac{27}{28}

, 5.

\frac{7}{10}

, 6.

\frac{13}{14}

, 7.

\frac{28}{29}

, 8.

\frac{7}{9}

, 9.

\frac{59}{100}

, 10.

\frac{5}{7}

, 11.

\frac{69}{100}

, 12.

\frac{43}{50}

, 13.

\frac{14}{15}

, 14.

\frac{3}{4}

, 15.

\frac{15}{17}

\frac{11}{17} + \frac{4}{17} =

\frac{44}{50}

, 2.

\frac{3}{5}

, 3.

\frac{5}{8}

, 4.

\frac{27}{28}

, 5.

\frac{7}{10}

, 6.

\frac{13}{14}

, 7.

\frac{28}{29}

, 8.

\frac{7}{9}

, 9.

\frac{59}{100}

, 10.

\frac{5}{7}

, 11.

\frac{69}{100}

, 12.

\frac{43}{50}

, 13.

\frac{14}{15}

, 14.

\frac{3}{4}

, 15.

\frac{15}{17}

\frac{15}{28} + \frac{12}{28} =

\frac{44}{50}

, 2.

\frac{3}{5}

, 3.

\frac{5}{8}

, 4.

\frac{27}{28}

, 5.

\frac{7}{10}

, 6.

\frac{13}{14}

, 7.

\frac{28}{29}

, 8.

\frac{7}{9}

, 9.

\frac{59}{100}

, 10.

\frac{5}{7}

, 11.

\frac{69}{100}

, 12.

\frac{43}{50}

, 13.

\frac{14}{15}

, 14.

\frac{3}{4}

, 15.

\frac{15}{17}

\frac{24}{50} + \frac{19}{50} =

\frac{44}{50}

, 2.

\frac{3}{5}

, 3.

\frac{5}{8}

, 4.

\frac{27}{28}

, 5.

\frac{7}{10}

, 6.

\frac{13}{14}

, 7.

\frac{28}{29}

, 8.

\frac{7}{9}

, 9.

\frac{59}{100}

, 10.

\frac{5}{7}

, 11.

\frac{69}{100}

, 12.

\frac{43}{50}

, 13.

\frac{14}{15}

, 14.

\frac{3}{4}

, 15.

\frac{15}{17}

\frac{25}{100} + \frac{34}{100} =

\frac{44}{50}

, 2.

\frac{3}{5}

, 3.

\frac{5}{8}

, 4.

\frac{27}{28}

, 5.

\frac{7}{10}

, 6.

\frac{13}{14}

, 7.

\frac{28}{29}

, 8.

\frac{7}{9}

, 9.

\frac{59}{100}

, 10.

\frac{5}{7}

, 11.

\frac{69}{100}

, 12.

\frac{43}{50}

, 13.

\frac{14}{15}

, 14.

\frac{3}{4}

, 15.

\frac{15}{17}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RugMBGHaKCnf1

Ćwiczenie 4

Oblicz, a następnie podaj wynik w postaci ułamka nieskracalnego. Uzupełnij odpowiedzi, przeciągając w luki odpowiednie liczby.

\frac{3}{8} + \frac{1}{8} =

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

=

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

\frac{2}{9} + \frac{4}{9} =

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

=

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

\frac{5}{12} + \frac{4}{12} =

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

=

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

\frac{8}{15} + \frac{4}{15} =

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

=

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

\frac{11}{24} + \frac{4}{24} =

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

=

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

\frac{3}{18} + \frac{9}{18} =

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

=

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

\frac{17}{36} + \frac{7}{36} =

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

=

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

\frac{21}{40} + \frac{9}{40} =

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

=

\frac{12}{18}

, 2.

\frac{3}{4}

, 3.

\frac{2}{3}

, 4.

\frac{15}{24}

, 5.

\frac{6}{9}

, 6.

\frac{24}{36}

, 7.

\frac{30}{40}

, 8.

\frac{9}{12}

, 9.

\frac{12}{15}

, 10.

\frac{4}{5}

, 11.

\frac{5}{8}

, 12.

\frac{2}{3}

, 13.

\frac{1}{2}

, 14.

\frac{4}{8}

, 15.

\frac{3}{4}

, 16.

\frac{2}{3}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1SmMW3hDrwHR

Ćwiczenie 5

Dodaj ułamki. Wynik wstaw najpierw w postaci ułamka, a następnie w postaci liczby mieszanej. Następnie skróć część ułamkową liczby mieszanej. Kliknij w lukę, aby rozwinąć listę, a następnie wybierz prawidłową liczbę.

\frac{5}{6} + \frac{4}{6} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{7}{9} + \frac{8}{9} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{11}{12} + \frac{10}{12} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{9}{15} + \frac{11}{15} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{3}{4} + \frac{2}{4} + \frac{1}{4} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{5}{8} + \frac{7}{8} + \frac{6}{8} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{8}{9} + \frac{8}{9} + \frac{8}{9} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{7}{10} + \frac{5}{10} + \frac{8}{10} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{5}{6} + \frac{4}{6} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{7}{9} + \frac{8}{9} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{11}{12} + \frac{10}{12} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{9}{15} + \frac{11}{15} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{3}{4} + \frac{2}{4} + \frac{1}{4} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{5}{8} + \frac{7}{8} + \frac{6}{8} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{8}{9} + \frac{8}{9} + \frac{8}{9} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

\frac{7}{10} + \frac{5}{10} + \frac{8}{10} =

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

=

2 \frac{2}{3}

, 2.

2 \frac{6}{9}

, 3.

2 \frac{2}{8}

, 4.

\frac{20}{15}

, 5.

1 \frac{9}{12}

, 6.

1 \frac{1}{3}

, 7.

\frac{6}{4}

, 8.

1 \frac{2}{4}

, 9.

\frac{24}{9}

, 10.

1 \frac{1}{2}

, 11.

\frac{9}{6}

, 12.

1 \frac{2}{3}

, 13.

\frac{21}{12}

, 14.

2

, 15.

1 \frac{5}{15}

, 16.

\frac{20}{10}

, 17.

1 \frac{1}{2}

, 18.

1 \frac{3}{4}

, 19.

1 \frac{6}{9}

, 20.

2 \frac{1}{4}

, 21.

\frac{15}{9}

, 22.

1 \frac{3}{6}

, 23.

\frac{18}{8}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RtFGEcZW8wQOk

Ćwiczenie 6

Oblicz podane różnice, a następnie uzupełnij równości, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.

\frac{3}{8} - \frac{2}{8} =

\frac{3}{8}

, 2.

\frac{23}{97}

, 3.

\frac{5}{17}

, 4.

\frac{3}{4}

, 5.

\frac{15}{49}

, 6.

\frac{6}{10}

, 7.

\frac{5}{14}

, 8.

\frac{3}{10}

, 9.

\frac{23}{95}

, 10.

\frac{9}{26}

, 11.

\frac{5}{15}

, 12.

\frac{13}{49}

, 13.

\frac{1}{8}

, 14.

\frac{1}{3}

, 15.

\frac{1}{4}

, 16.

\frac{3}{17}

, 17.

\frac{15}{47}

, 18.

\frac{1}{6}

, 19.

\frac{7}{17}

, 20.

\frac{21}{95}

, 21.

\frac{3}{12}

, 22.

\frac{11}{28}

, 23.

\frac{9}{28}

, 24.

\frac{7}{14}

\frac{2}{4} - \frac{1}{4} =

\frac{3}{8}

, 2.

\frac{23}{97}

, 3.

\frac{5}{17}

, 4.

\frac{3}{4}

, 5.

\frac{15}{49}

, 6.

\frac{6}{10}

, 7.

\frac{5}{14}

, 8.

\frac{3}{10}

, 9.

\frac{23}{95}

, 10.

\frac{9}{26}

, 11.

\frac{5}{15}

, 12.

\frac{13}{49}

, 13.

\frac{1}{8}

, 14.

\frac{1}{3}

, 15.

\frac{1}{4}

, 16.

\frac{3}{17}

, 17.

\frac{15}{47}

, 18.

\frac{1}{6}

, 19.

\frac{7}{17}

, 20.

\frac{21}{95}

, 21.

\frac{3}{12}

, 22.

\frac{11}{28}

, 23.

\frac{9}{28}

, 24.

\frac{7}{14}

\frac{5}{10} - \frac{2}{10} =

\frac{3}{8}

, 2.

\frac{23}{97}

, 3.

\frac{5}{17}

, 4.

\frac{3}{4}

, 5.

\frac{15}{49}

, 6.

\frac{6}{10}

, 7.

\frac{5}{14}

, 8.

\frac{3}{10}

, 9.

\frac{23}{95}

, 10.

\frac{9}{26}

, 11.

\frac{5}{15}

, 12.

\frac{13}{49}

, 13.

\frac{1}{8}

, 14.

\frac{1}{3}

, 15.

\frac{1}{4}

, 16.

\frac{3}{17}

, 17.

\frac{15}{47}

, 18.

\frac{1}{6}

, 19.

\frac{7}{17}

, 20.

\frac{21}{95}

, 21.

\frac{3}{12}

, 22.

\frac{11}{28}

, 23.

\frac{9}{28}

, 24.

\frac{7}{14}

\frac{9}{14} - \frac{4}{14} =

\frac{3}{8}

, 2.

\frac{23}{97}

, 3.

\frac{5}{17}

, 4.

\frac{3}{4}

, 5.

\frac{15}{49}

, 6.

\frac{6}{10}

, 7.

\frac{5}{14}

, 8.

\frac{3}{10}

, 9.

\frac{23}{95}

, 10.

\frac{9}{26}

, 11.

\frac{5}{15}

, 12.

\frac{13}{49}

, 13.

\frac{1}{8}

, 14.

\frac{1}{3}

, 15.

\frac{1}{4}

, 16.

\frac{3}{17}

, 17.

\frac{15}{47}

, 18.

\frac{1}{6}

, 19.

\frac{7}{17}

, 20.

\frac{21}{95}

, 21.

\frac{3}{12}

, 22.

\frac{11}{28}

, 23.

\frac{9}{28}

, 24.

\frac{7}{14}

\frac{11}{17} - \frac{4}{17} =

\frac{3}{8}

, 2.

\frac{23}{97}

, 3.

\frac{5}{17}

, 4.

\frac{3}{4}

, 5.

\frac{15}{49}

, 6.

\frac{6}{10}

, 7.

\frac{5}{14}

, 8.

\frac{3}{10}

, 9.

\frac{23}{95}

, 10.

\frac{9}{26}

, 11.

\frac{5}{15}

, 12.

\frac{13}{49}

, 13.

\frac{1}{8}

, 14.

\frac{1}{3}

, 15.

\frac{1}{4}

, 16.

\frac{3}{17}

, 17.

\frac{15}{47}

, 18.

\frac{1}{6}

, 19.

\frac{7}{17}

, 20.

\frac{21}{95}

, 21.

\frac{3}{12}

, 22.

\frac{11}{28}

, 23.

\frac{9}{28}

, 24.

\frac{7}{14}

\frac{21}{28} - \frac{12}{28} =

\frac{3}{8}

, 2.

\frac{23}{97}

, 3.

\frac{5}{17}

, 4.

\frac{3}{4}

, 5.

\frac{15}{49}

, 6.

\frac{6}{10}

, 7.

\frac{5}{14}

, 8.

\frac{3}{10}

, 9.

\frac{23}{95}

, 10.

\frac{9}{26}

, 11.

\frac{5}{15}

, 12.

\frac{13}{49}

, 13.

\frac{1}{8}

, 14.

\frac{1}{3}

, 15.

\frac{1}{4}

, 16.

\frac{3}{17}

, 17.

\frac{15}{47}

, 18.

\frac{1}{6}

, 19.

\frac{7}{17}

, 20.

\frac{21}{95}

, 21.

\frac{3}{12}

, 22.

\frac{11}{28}

, 23.

\frac{9}{28}

, 24.

\frac{7}{14}

\frac{34}{49} - \frac{19}{49} =

\frac{3}{8}

, 2.

\frac{23}{97}

, 3.

\frac{5}{17}

, 4.

\frac{3}{4}

, 5.

\frac{15}{49}

, 6.

\frac{6}{10}

, 7.

\frac{5}{14}

, 8.

\frac{3}{10}

, 9.

\frac{23}{95}

, 10.

\frac{9}{26}

, 11.

\frac{5}{15}

, 12.

\frac{13}{49}

, 13.

\frac{1}{8}

, 14.

\frac{1}{3}

, 15.

\frac{1}{4}

, 16.

\frac{3}{17}

, 17.

\frac{15}{47}

, 18.

\frac{1}{6}

, 19.

\frac{7}{17}

, 20.

\frac{21}{95}

, 21.

\frac{3}{12}

, 22.

\frac{11}{28}

, 23.

\frac{9}{28}

, 24.

\frac{7}{14}

\frac{54}{97} - \frac{31}{97} =

\frac{3}{8}

, 2.

\frac{23}{97}

, 3.

\frac{5}{17}

, 4.

\frac{3}{4}

, 5.

\frac{15}{49}

, 6.

\frac{6}{10}

, 7.

\frac{5}{14}

, 8.

\frac{3}{10}

, 9.

\frac{23}{95}

, 10.

\frac{9}{26}

, 11.

\frac{5}{15}

, 12.

\frac{13}{49}

, 13.

\frac{1}{8}

, 14.

\frac{1}{3}

, 15.

\frac{1}{4}

, 16.

\frac{3}{17}

, 17.

\frac{15}{47}

, 18.

\frac{1}{6}

, 19.

\frac{7}{17}

, 20.

\frac{21}{95}

, 21.

\frac{3}{12}

, 22.

\frac{11}{28}

, 23.

\frac{9}{28}

, 24.

\frac{7}{14}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RrstWL6aZczn5

Ćwiczenie 7

Oblicz różnice i przedstaw wynik w postaci ułamka nieskracalnego, a następnie uzupełnij równości, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.

\frac{3}{8} - \frac{1}{8} =

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

=

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

\frac{4}{9} - \frac{1}{9} =

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

=

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

\frac{9}{12} - \frac{1}{12} =

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

=

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

\frac{14}{15} - \frac{2}{15} =

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

=

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

\frac{11}{24} - \frac{3}{24} =

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

=

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

\frac{13}{18} - \frac{11}{18} =

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

=

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

\frac{17}{36} - \frac{7}{36} =

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

=

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

\frac{21}{40} - \frac{13}{40} =

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

=

\frac{1}{9}

, 2.

\frac{2}{8}

, 3.

\frac{10}{36}

, 4.

\frac{3}{9}

, 5.

\frac{4}{5}

, 6.

\frac{1}{5}

, 7.

\frac{1}{4}

, 8.

\frac{1}{3}

, 9.

\frac{5}{18}

, 10.

\frac{2}{18}

, 11.

\frac{1}{3}

, 12.

\frac{2}{3}

, 13.

\frac{8}{24}

, 14.

\frac{8}{40}

, 15.

\frac{12}{15}

, 16.

\frac{8}{12}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rjf544u51fu2M

Ćwiczenie 8

Oblicz różnice i wyniki przedstaw najpierw w postaci ułamków niewłaściwych, potem w postaci liczb mieszanych, a następnie uzupełnij równości, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.

\frac{11}{6} - \frac{3}{6} =

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

\frac{13}{9} - \frac{1}{9} =

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

\frac{19}{12} - \frac{5}{12} =

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

\frac{34}{15} - \frac{1}{15} =

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

\frac{19}{4} - \frac{5}{4} =

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

\frac{29}{8} - \frac{3}{8} =

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

\frac{11}{6} - \frac{3}{6} =

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

\frac{13}{9} - \frac{1}{9} =

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

\frac{19}{12} - \frac{5}{12} =

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

\frac{34}{15} - \frac{1}{15} =

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

\frac{19}{4} - \frac{5}{4} =

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

\frac{29}{8} - \frac{3}{8} =

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

=

1 \frac{2}{6}

, 2.

2 \frac{1}{5}

, 3.

\frac{8}{6}

, 4.

1 \frac{1}{6}

, 5.

\frac{33}{15}

, 6.

\frac{14}{4}

, 7.

\frac{26}{8}

, 8.

3 \frac{1}{2}

, 9.

1 \frac{1}{3}

, 10.

\frac{14}{12}

, 11.

2 \frac{3}{15}

, 12.

3 \frac{1}{4}

, 13.

3 \frac{2}{8}

, 14.

3 \frac{2}{4}

, 15.

1 \frac{3}{9}

, 16.

1 \frac{1}{3}

, 17.

1 \frac{2}{12}

, 18.

\frac{12}{9}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1Pu83IEiYK1C

Ćwiczenie 9

Uzupełnij poniższe równości odpowiednimi liczbami. Kliknij w lukę, aby rozwinąć listę i wybierz brakującą liczbę dla każdej równości.

\frac{1}{4} + \frac{1}{4} =

\frac{1}{3}

, 2.

1

, 3.

2 \frac{1}{5}

, 4.

\frac{1}{4}

, 5.

2 \frac{1}{6}

, 6.

\frac{2}{5}

, 7.

\frac{3}{4}

, 8.

\frac{3}{5}

, 9.

\frac{1}{2}

, 10.

\frac{1}{2}

, 11.

\frac{2}{3}

, 12.

1 \frac{1}{5}

\frac{1}{9} + \frac{5}{9} =

\frac{1}{3}

, 2.

1

, 3.

2 \frac{1}{5}

, 4.

\frac{1}{4}

, 5.

2 \frac{1}{6}

, 6.

\frac{2}{5}

, 7.

\frac{3}{4}

, 8.

\frac{3}{5}

, 9.

\frac{1}{2}

, 10.

\frac{1}{2}

, 11.

\frac{2}{3}

, 12.

1 \frac{1}{5}

\frac{3}{10} + \frac{7}{10} =

\frac{1}{3}

, 2.

1

, 3.

2 \frac{1}{5}

, 4.

\frac{1}{4}

, 5.

2 \frac{1}{6}

, 6.

\frac{2}{5}

, 7.

\frac{3}{4}

, 8.

\frac{3}{5}

, 9.

\frac{1}{2}

, 10.

\frac{1}{2}

, 11.

\frac{2}{3}

, 12.

1 \frac{1}{5}

\frac{5}{12} + \frac{4}{12} =

\frac{1}{3}

, 2.

1

, 3.

2 \frac{1}{5}

, 4.

\frac{1}{4}

, 5.

2 \frac{1}{6}

, 6.

\frac{2}{5}

, 7.

\frac{3}{4}

, 8.

\frac{3}{5}

, 9.

\frac{1}{2}

, 10.

\frac{1}{2}

, 11.

\frac{2}{3}

, 12.

1 \frac{1}{5}

\frac{11}{15} + \frac{7}{15} =

\frac{1}{3}

, 2.

1

, 3.

2 \frac{1}{5}

, 4.

\frac{1}{4}

, 5.

2 \frac{1}{6}

, 6.

\frac{2}{5}

, 7.

\frac{3}{4}

, 8.

\frac{3}{5}

, 9.

\frac{1}{2}

, 10.

\frac{1}{2}

, 11.

\frac{2}{3}

, 12.

1 \frac{1}{5}

\frac{3}{6} + \frac{5}{6} + \frac{5}{6} =

\frac{1}{3}

, 2.

1

, 3.

2 \frac{1}{5}

, 4.

\frac{1}{4}

, 5.

2 \frac{1}{6}

, 6.

\frac{2}{5}

, 7.

\frac{3}{4}

, 8.

\frac{3}{5}

, 9.

\frac{1}{2}

, 10.

\frac{1}{2}

, 11.

\frac{2}{3}

, 12.

1 \frac{1}{5}

\frac{7}{8} - \frac{3}{8} =

\frac{1}{3}

, 2.

1

, 3.

2 \frac{1}{5}

, 4.

\frac{1}{4}

, 5.

2 \frac{1}{6}

, 6.

\frac{2}{5}

, 7.

\frac{3}{4}

, 8.

\frac{3}{5}

, 9.

\frac{1}{2}

, 10.

\frac{1}{2}

, 11.

\frac{2}{3}

, 12.

1 \frac{1}{5}

\frac{13}{16} - \frac{9}{16} =

\frac{1}{3}

, 2.

1

, 3.

2 \frac{1}{5}

, 4.

\frac{1}{4}

, 5.

2 \frac{1}{6}

, 6.

\frac{2}{5}

, 7.

\frac{3}{4}

, 8.

\frac{3}{5}

, 9.

\frac{1}{2}

, 10.

\frac{1}{2}

, 11.

\frac{2}{3}

, 12.

1 \frac{1}{5}

1 - \frac{18}{30} =

\frac{1}{3}

, 2.

1

, 3.

2 \frac{1}{5}

, 4.

\frac{1}{4}

, 5.

2 \frac{1}{6}

, 6.

\frac{2}{5}

, 7.

\frac{3}{4}

, 8.

\frac{3}{5}

, 9.

\frac{1}{2}

, 10.

\frac{1}{2}

, 11.

\frac{2}{3}

, 12.

1 \frac{1}{5}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Dodawanie i odejmowanie liczb mieszanych

Przykład 5

Chcąc dodać dwie liczby mieszane, nie musimy zamieniać tych liczb na ułamki niewłaściwe.

R1GOdJ9lFaOv51

Ważne!

Aby dodać liczby mieszane, należy dodać najpierw części całkowite, a następnie części ułamkowe.

$2 \frac{3}{6} + 1 \frac{2}{6} = 3 \frac{5}{6}$

Jeśli suma części ułamkowych jest ułamkiem niewłaściwym, wyłączamy z niego całości.

$6 \frac{5}{8} + 2 \frac{4}{8} = 8 \frac{9}{8} = 9 \frac{1}{8}$

$\frac{9}{8} = 1 \frac{1}{8}$

więc

$1 \frac{1}{8} + 8 = 9 \frac{1}{8}$

Przykład 6

Chcąc odjąć dwie liczby mieszane, możemy zamienić najpierw obie liczby na ułamki niewłaściwe, a następnie wykonać odejmowanie ułamków.

R154RYIdeUKFu

Przykład 7

Jacek organizował biwak dla harcerzy. Kupił $7 \frac{6}{10} kg$ kiełbasy, $4 \frac{8}{10} kg$ chleba oraz $3 \frac{3}{10} kg$ ziemniaków.

Ile ważyły wszystkie zakupione przez Jacka produkty?

$7 \frac{6}{10} + 4 \frac{8}{10} + 3 \frac{3}{10} = 14 \frac{17}{10} = 15 \frac{7}{10}$ .

Odp.: Wszystkie produkty ważyły $15 \frac{7}{10} kg$ .

O ile kilogramów więcej kupił Jacek kiełbasy niż ziemniaków?

$7 \frac{6}{10} - 3 \frac{3}{10} = 4 \frac{3}{10}$ .

Odp.: Jacek kupił o $4 \frac{3}{10} kg$ kiełbasy więcej niż ziemniaków.

O ile kilogramów więcej kupił Jacek kiełbasy niż chleba?

$7 \frac{6}{10} - 4 \frac{8}{10} = 6 \frac{16}{10} - 4 \frac{8}{10} = 2 \frac{8}{10} = 2 \frac{4}{5}$ .

Odp.: Jacek kupił o $2 \frac{4}{5} kg$ kiełbasy więcej niż chleba.

Ważne!

Dodając liczby mieszane, możemy obliczyć sumę części całkowitych i sumę części ułamkowych. Pamiętamy, aby wynik zapisać w najprostszej postaci, po wyłączeniu całości i skróceniu części ułamkowej.

Ważne!

Aby odjąć liczby mieszane, można najpierw odjąć ich części całkowite, a następnie części ułamkowe.

$4 \frac{3}{6} - 1 \frac{2}{6} = 3 \frac{1}{6}$

Gdy licznik ułamka odjemnej jest mniejszy od licznika odjemnika, jedną całość pierwszej liczby zamieniamy na ułamek.

$6 \frac{4}{8} - 2 \frac{5}{8} = 5 \frac{12}{8} - 2 \frac{5}{8} = 3 \frac{7}{8}$

R1GukrQw0Bk5U1

Rysunek czternastu prostokątów, które ilustrują równość ułamków: sześć całych i cztery ósme równa się pięć całych i dwanaście ósmych. Po lewej stronie znajduje się siedem prostokątów, z czego ostatni podzielony jest na osiem równych kwadratów. Zamalowanych jest sześć całych prostokątów oraz cztery mniejsze kwadraty. Po prawej stronie znajduje się siedem prostokątów, z czego dwa ostatnie podzielone są na osiem równych kwadratów każdy. Zamalowanych jest pięć całych prostokątów, jeden cały prostokąt podzielony na osiem części oraz cztery mniejsze kwadraty ostatniego prostokąta. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 10

Zastanów się jakie dodawanie zilustrowane jest rysunkiem, a następnie przeciągnij odpowiednie liczby mieszane w puste pola na grafikach.

RqwCKzY157Zfb
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1505HRGiC4FM
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RlR4tpiA3v8tI
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1b3ZZkUuzaEr

Uzupełnij zdania. Kliknij w lukę, aby rozwinąć listę, a następnie wybierz prawidłową równość. Pierwszy rysunek przedstawia pewne dodawanie. Do jednego całego paska i jednej z pięciu części paska dodano dwa paski i dwie z pięciu części paska. Otrzymano trzy całe paski i cztery z pięciu części paska. Ten rysunek ilustruje dodawanie 1.

1 \frac{3}{4} + 2 \frac{3}{4} + 1 \frac{1}{4} = 4 \frac{7}{4} = 5 \frac{3}{4}

, 2.

1 \frac{1}{5} + 2 \frac{3}{5} = 3 \frac{4}{5}

, 3.

3 \frac{4}{7} + 5 \frac{2}{7} = 8 \frac{6}{7}

, 4.

1 \frac{2}{5} + 2 \frac{2}{5} = 3 \frac{4}{5}

, 5.

1 \frac{1}{4} + 2 \frac{2}{4} + 1 \frac{1}{4} = 5

.Drugi rysunek przedstawia pewne dodawanie. Do trzech całych pasków i czterech z siedmiu części paska dodano pięć pasów i dwie z siedmiu części paska. Otrzymano osiem całych pasków i sześć z siedmiu części paska. Ten rysunek ilustruje dodawanie 1.

1 \frac{3}{4} + 2 \frac{3}{4} + 1 \frac{1}{4} = 4 \frac{7}{4} = 5 \frac{3}{4}

, 2.

1 \frac{1}{5} + 2 \frac{3}{5} = 3 \frac{4}{5}

, 3.

3 \frac{4}{7} + 5 \frac{2}{7} = 8 \frac{6}{7}

, 4.

1 \frac{2}{5} + 2 \frac{2}{5} = 3 \frac{4}{5}

, 5.

1 \frac{1}{4} + 2 \frac{2}{4} + 1 \frac{1}{4} = 5

.Trzeci rysunek przedstawia pewne dodawanie. Do jednego paska i trzech z czterech części paska dodano dwa paski i trzy z czterech części paska oraz dodano jeden pasek i jedną z czterech części paska. Otrzymano cztery całe paski, jeden cały pasek złożony z czterech równych części i trzy z czterech części paska. Ten rysunek ilustruje dodawanie 1.

1 \frac{3}{4} + 2 \frac{3}{4} + 1 \frac{1}{4} = 4 \frac{7}{4} = 5 \frac{3}{4}

, 2.

1 \frac{1}{5} + 2 \frac{3}{5} = 3 \frac{4}{5}

, 3.

3 \frac{4}{7} + 5 \frac{2}{7} = 8 \frac{6}{7}

, 4.

1 \frac{2}{5} + 2 \frac{2}{5} = 3 \frac{4}{5}

, 5.

1 \frac{1}{4} + 2 \frac{2}{4} + 1 \frac{1}{4} = 5

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rt1nKD5eLpHRv

Ćwiczenie 11

Oblicz. Liczbę mieszaną zapisz w takiej postaci, w której wszystkie całości są wyłączone, a ułamek jest nieskracalny. Uzupełnij równości, przeciągając w luki odpowiednie liczby.

1 \frac{3}{7} + 3 \frac{1}{7} =

7 \frac{2}{3}

, 2.

8 \frac{3}{4}

, 3.

11 \frac{1}{3}

, 4.

8 \frac{4}{5}

, 5.

5 \frac{1}{6}

, 6.

8 \frac{2}{3}

, 7.

3 \frac{1}{6}

, 8.

7 \frac{1}{3}

, 9.

1 \frac{3}{5}

, 10.

1 \frac{2}{5}

, 11.

9 \frac{1}{4}

, 12.

8 \frac{2}{5}

, 13.

9 \frac{1}{2}

, 14.

3

, 15.

5 \frac{4}{7}

, 16.

3 \frac{1}{4}

, 17.

5 \frac{5}{6}

, 18.

12 \frac{1}{3}

, 19.

4

, 20.

4 \frac{1}{4}

, 21.

4 \frac{3}{4}

, 22.

4 \frac{4}{7}

3 \frac{1}{4} + 5 \frac{2}{4} =

7 \frac{2}{3}

, 2.

8 \frac{3}{4}

, 3.

11 \frac{1}{3}

, 4.

8 \frac{4}{5}

, 5.

5 \frac{1}{6}

, 6.

8 \frac{2}{3}

, 7.

3 \frac{1}{6}

, 8.

7 \frac{1}{3}

, 9.

1 \frac{3}{5}

, 10.

1 \frac{2}{5}

, 11.

9 \frac{1}{4}

, 12.

8 \frac{2}{5}

, 13.

9 \frac{1}{2}

, 14.

3

, 15.

5 \frac{4}{7}

, 16.

3 \frac{1}{4}

, 17.

5 \frac{5}{6}

, 18.

12 \frac{1}{3}

, 19.

4

, 20.

4 \frac{1}{4}

, 21.

4 \frac{3}{4}

, 22.

4 \frac{4}{7}

2 \frac{2}{9} + 5 \frac{4}{9} =

7 \frac{2}{3}

, 2.

8 \frac{3}{4}

, 3.

11 \frac{1}{3}

, 4.

8 \frac{4}{5}

, 5.

5 \frac{1}{6}

, 6.

8 \frac{2}{3}

, 7.

3 \frac{1}{6}

, 8.

7 \frac{1}{3}

, 9.

1 \frac{3}{5}

, 10.

1 \frac{2}{5}

, 11.

9 \frac{1}{4}

, 12.

8 \frac{2}{5}

, 13.

9 \frac{1}{2}

, 14.

3

, 15.

5 \frac{4}{7}

, 16.

3 \frac{1}{4}

, 17.

5 \frac{5}{6}

, 18.

12 \frac{1}{3}

, 19.

4

, 20.

4 \frac{1}{4}

, 21.

4 \frac{3}{4}

, 22.

4 \frac{4}{7}

4 \frac{3}{8} + \frac{3}{8} =

7 \frac{2}{3}

, 2.

8 \frac{3}{4}

, 3.

11 \frac{1}{3}

, 4.

8 \frac{4}{5}

, 5.

5 \frac{1}{6}

, 6.

8 \frac{2}{3}

, 7.

3 \frac{1}{6}

, 8.

7 \frac{1}{3}

, 9.

1 \frac{3}{5}

, 10.

1 \frac{2}{5}

, 11.

9 \frac{1}{4}

, 12.

8 \frac{2}{5}

, 13.

9 \frac{1}{2}

, 14.

3

, 15.

5 \frac{4}{7}

, 16.

3 \frac{1}{4}

, 17.

5 \frac{5}{6}

, 18.

12 \frac{1}{3}

, 19.

4

, 20.

4 \frac{1}{4}

, 21.

4 \frac{3}{4}

, 22.

4 \frac{4}{7}

2 \frac{2}{5} + \frac{3}{5} =

7 \frac{2}{3}

, 2.

8 \frac{3}{4}

, 3.

11 \frac{1}{3}

, 4.

8 \frac{4}{5}

, 5.

5 \frac{1}{6}

, 6.

8 \frac{2}{3}

, 7.

3 \frac{1}{6}

, 8.

7 \frac{1}{3}

, 9.

1 \frac{3}{5}

, 10.

1 \frac{2}{5}

, 11.

9 \frac{1}{4}

, 12.

8 \frac{2}{5}

, 13.

9 \frac{1}{2}

, 14.

3

, 15.

5 \frac{4}{7}

, 16.

3 \frac{1}{4}

, 17.

5 \frac{5}{6}

, 18.

12 \frac{1}{3}

, 19.

4

, 20.

4 \frac{1}{4}

, 21.

4 \frac{3}{4}

, 22.

4 \frac{4}{7}

1 \frac{5}{6} + 3 \frac{2}{6} =

7 \frac{2}{3}

, 2.

8 \frac{3}{4}

, 3.

11 \frac{1}{3}

, 4.

8 \frac{4}{5}

, 5.

5 \frac{1}{6}

, 6.

8 \frac{2}{3}

, 7.

3 \frac{1}{6}

, 8.

7 \frac{1}{3}

, 9.

1 \frac{3}{5}

, 10.

1 \frac{2}{5}

, 11.

9 \frac{1}{4}

, 12.

8 \frac{2}{5}

, 13.

9 \frac{1}{2}

, 14.

3

, 15.

5 \frac{4}{7}

, 16.

3 \frac{1}{4}

, 17.

5 \frac{5}{6}

, 18.

12 \frac{1}{3}

, 19.

4

, 20.

4 \frac{1}{4}

, 21.

4 \frac{3}{4}

, 22.

4 \frac{4}{7}

3 \frac{2}{3} + 8 \frac{2}{3} =

7 \frac{2}{3}

, 2.

8 \frac{3}{4}

, 3.

11 \frac{1}{3}

, 4.

8 \frac{4}{5}

, 5.

5 \frac{1}{6}

, 6.

8 \frac{2}{3}

, 7.

3 \frac{1}{6}

, 8.

7 \frac{1}{3}

, 9.

1 \frac{3}{5}

, 10.

1 \frac{2}{5}

, 11.

9 \frac{1}{4}

, 12.

8 \frac{2}{5}

, 13.

9 \frac{1}{2}

, 14.

3

, 15.

5 \frac{4}{7}

, 16.

3 \frac{1}{4}

, 17.

5 \frac{5}{6}

, 18.

12 \frac{1}{3}

, 19.

4

, 20.

4 \frac{1}{4}

, 21.

4 \frac{3}{4}

, 22.

4 \frac{4}{7}

3 \frac{1}{2} + 5 \frac{1}{2} + \frac{1}{2} =

7 \frac{2}{3}

, 2.

8 \frac{3}{4}

, 3.

11 \frac{1}{3}

, 4.

8 \frac{4}{5}

, 5.

5 \frac{1}{6}

, 6.

8 \frac{2}{3}

, 7.

3 \frac{1}{6}

, 8.

7 \frac{1}{3}

, 9.

1 \frac{3}{5}

, 10.

1 \frac{2}{5}

, 11.

9 \frac{1}{4}

, 12.

8 \frac{2}{5}

, 13.

9 \frac{1}{2}

, 14.

3

, 15.

5 \frac{4}{7}

, 16.

3 \frac{1}{4}

, 17.

5 \frac{5}{6}

, 18.

12 \frac{1}{3}

, 19.

4

, 20.

4 \frac{1}{4}

, 21.

4 \frac{3}{4}

, 22.

4 \frac{4}{7}

\frac{9}{10} + \frac{7}{10} =

7 \frac{2}{3}

, 2.

8 \frac{3}{4}

, 3.

11 \frac{1}{3}

, 4.

8 \frac{4}{5}

, 5.

5 \frac{1}{6}

, 6.

8 \frac{2}{3}

, 7.

3 \frac{1}{6}

, 8.

7 \frac{1}{3}

, 9.

1 \frac{3}{5}

, 10.

1 \frac{2}{5}

, 11.

9 \frac{1}{4}

, 12.

8 \frac{2}{5}

, 13.

9 \frac{1}{2}

, 14.

3

, 15.

5 \frac{4}{7}

, 16.

3 \frac{1}{4}

, 17.

5 \frac{5}{6}

, 18.

12 \frac{1}{3}

, 19.

4

, 20.

4 \frac{1}{4}

, 21.

4 \frac{3}{4}

, 22.

4 \frac{4}{7}

\frac{11}{12} + 1 \frac{15}{12} =

7 \frac{2}{3}

, 2.

8 \frac{3}{4}

, 3.

11 \frac{1}{3}

, 4.

8 \frac{4}{5}

, 5.

5 \frac{1}{6}

, 6.

8 \frac{2}{3}

, 7.

3 \frac{1}{6}

, 8.

7 \frac{1}{3}

, 9.

1 \frac{3}{5}

, 10.

1 \frac{2}{5}

, 11.

9 \frac{1}{4}

, 12.

8 \frac{2}{5}

, 13.

9 \frac{1}{2}

, 14.

3

, 15.

5 \frac{4}{7}

, 16.

3 \frac{1}{4}

, 17.

5 \frac{5}{6}

, 18.

12 \frac{1}{3}

, 19.

4

, 20.

4 \frac{1}{4}

, 21.

4 \frac{3}{4}

, 22.

4 \frac{4}{7}

4 \frac{8}{15} + 3 \frac{13}{15} =

7 \frac{2}{3}

, 2.

8 \frac{3}{4}

, 3.

11 \frac{1}{3}

, 4.

8 \frac{4}{5}

, 5.

5 \frac{1}{6}

, 6.

8 \frac{2}{3}

, 7.

3 \frac{1}{6}

, 8.

7 \frac{1}{3}

, 9.

1 \frac{3}{5}

, 10.

1 \frac{2}{5}

, 11.

9 \frac{1}{4}

, 12.

8 \frac{2}{5}

, 13.

9 \frac{1}{2}

, 14.

3

, 15.

5 \frac{4}{7}

, 16.

3 \frac{1}{4}

, 17.

5 \frac{5}{6}

, 18.

12 \frac{1}{3}

, 19.

4

, 20.

4 \frac{1}{4}

, 21.

4 \frac{3}{4}

, 22.

4 \frac{4}{7}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Re8265mnEGQKC

Ćwiczenie 12

Dodaj ułamki, a następnie uzupełnij luki odpowiednimi liczbami. Kliknij w lukę, aby rozwinąć listę i wybierz brakującą liczbę dla każdej równości.

\frac{3}{16} + \frac{5}{16} =

1

, 2.

2 \frac{1}{4}

, 3.

2 \frac{1}{2}

, 4.

\frac{1}{4}

, 5.

2

, 6.

\frac{1}{2}

, 7.

\frac{3}{4}

, 8.

2 \frac{1}{2}

, 9.

2 \frac{3}{4}

, 10.

1 \frac{3}{8}

, 11.

2 \frac{1}{8}

\frac{1}{8} + \frac{5}{8} =

1

, 2.

2 \frac{1}{4}

, 3.

2 \frac{1}{2}

, 4.

\frac{1}{4}

, 5.

2

, 6.

\frac{1}{2}

, 7.

\frac{3}{4}

, 8.

2 \frac{1}{2}

, 9.

2 \frac{3}{4}

, 10.

1 \frac{3}{8}

, 11.

2 \frac{1}{8}

\frac{3}{4} + \frac{7}{4} =

1

, 2.

2 \frac{1}{4}

, 3.

2 \frac{1}{2}

, 4.

\frac{1}{4}

, 5.

2

, 6.

\frac{1}{2}

, 7.

\frac{3}{4}

, 8.

2 \frac{1}{2}

, 9.

2 \frac{3}{4}

, 10.

1 \frac{3}{8}

, 11.

2 \frac{1}{8}

\frac{3}{4} + \frac{1}{4} =

1

, 2.

2 \frac{1}{4}

, 3.

2 \frac{1}{2}

, 4.

\frac{1}{4}

, 5.

2

, 6.

\frac{1}{2}

, 7.

\frac{3}{4}

, 8.

2 \frac{1}{2}

, 9.

2 \frac{3}{4}

, 10.

1 \frac{3}{8}

, 11.

2 \frac{1}{8}

1 \frac{1}{16} + \frac{15}{16} =

1

, 2.

2 \frac{1}{4}

, 3.

2 \frac{1}{2}

, 4.

\frac{1}{4}

, 5.

2

, 6.

\frac{1}{2}

, 7.

\frac{3}{4}

, 8.

2 \frac{1}{2}

, 9.

2 \frac{3}{4}

, 10.

1 \frac{3}{8}

, 11.

2 \frac{1}{8}

1 \frac{3}{8} + \frac{7}{8} =

1

, 2.

2 \frac{1}{4}

, 3.

2 \frac{1}{2}

, 4.

\frac{1}{4}

, 5.

2

, 6.

\frac{1}{2}

, 7.

\frac{3}{4}

, 8.

2 \frac{1}{2}

, 9.

2 \frac{3}{4}

, 10.

1 \frac{3}{8}

, 11.

2 \frac{1}{8}

1 \frac{3}{4} + \frac{3}{4} =

1

, 2.

2 \frac{1}{4}

, 3.

2 \frac{1}{2}

, 4.

\frac{1}{4}

, 5.

2

, 6.

\frac{1}{2}

, 7.

\frac{3}{4}

, 8.

2 \frac{1}{2}

, 9.

2 \frac{3}{4}

, 10.

1 \frac{3}{8}

, 11.

2 \frac{1}{8}

1 \frac{3}{16} + \frac{15}{16} =

1

, 2.

2 \frac{1}{4}

, 3.

2 \frac{1}{2}

, 4.

\frac{1}{4}

, 5.

2

, 6.

\frac{1}{2}

, 7.

\frac{3}{4}

, 8.

2 \frac{1}{2}

, 9.

2 \frac{3}{4}

, 10.

1 \frac{3}{8}

, 11.

2 \frac{1}{8}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1ewScQEJoePV

Ćwiczenie 13

Dodaj ułamki, a następnie uzupełnij luki odpowiednimi liczbami. Kliknij w lukę, aby rozwinąć listę i wybierz brakującą liczbę dla każdej równości.

\frac{5}{12} + \frac{1}{12} =

\frac{4}{5}

, 2.

\frac{1}{4}

, 3.

1 \frac{1}{2}

, 4.

2 \frac{1}{3}

, 5.

1

, 6.

1 \frac{5}{12}

, 7.

2 \frac{1}{6}

, 8.

\frac{1}{2}

, 9.

\frac{5}{6}

, 10.

2 \frac{2}{3}

, 11.

2 \frac{1}{3}

\frac{1}{6} + \frac{4}{6} =

\frac{4}{5}

, 2.

\frac{1}{4}

, 3.

1 \frac{1}{2}

, 4.

2 \frac{1}{3}

, 5.

1

, 6.

1 \frac{5}{12}

, 7.

2 \frac{1}{6}

, 8.

\frac{1}{2}

, 9.

\frac{5}{6}

, 10.

2 \frac{2}{3}

, 11.

2 \frac{1}{3}

\frac{1}{3} + \frac{2}{3} =

\frac{4}{5}

, 2.

\frac{1}{4}

, 3.

1 \frac{1}{2}

, 4.

2 \frac{1}{3}

, 5.

1

, 6.

1 \frac{5}{12}

, 7.

2 \frac{1}{6}

, 8.

\frac{1}{2}

, 9.

\frac{5}{6}

, 10.

2 \frac{2}{3}

, 11.

2 \frac{1}{3}

\frac{1}{24} + \frac{5}{24} =

\frac{4}{5}

, 2.

\frac{1}{4}

, 3.

1 \frac{1}{2}

, 4.

2 \frac{1}{3}

, 5.

1

, 6.

1 \frac{5}{12}

, 7.

2 \frac{1}{6}

, 8.

\frac{1}{2}

, 9.

\frac{5}{6}

, 10.

2 \frac{2}{3}

, 11.

2 \frac{1}{3}

1 \frac{3}{12} + \frac{11}{12} =

\frac{4}{5}

, 2.

\frac{1}{4}

, 3.

1 \frac{1}{2}

, 4.

2 \frac{1}{3}

, 5.

1

, 6.

1 \frac{5}{12}

, 7.

2 \frac{1}{6}

, 8.

\frac{1}{2}

, 9.

\frac{5}{6}

, 10.

2 \frac{2}{3}

, 11.

2 \frac{1}{3}

1 \frac{3}{6} + \frac{5}{6} =

\frac{4}{5}

, 2.

\frac{1}{4}

, 3.

1 \frac{1}{2}

, 4.

2 \frac{1}{3}

, 5.

1

, 6.

1 \frac{5}{12}

, 7.

2 \frac{1}{6}

, 8.

\frac{1}{2}

, 9.

\frac{5}{6}

, 10.

2 \frac{2}{3}

, 11.

2 \frac{1}{3}

1 \frac{2}{3} + \frac{2}{3} =

\frac{4}{5}

, 2.

\frac{1}{4}

, 3.

1 \frac{1}{2}

, 4.

2 \frac{1}{3}

, 5.

1

, 6.

1 \frac{5}{12}

, 7.

2 \frac{1}{6}

, 8.

\frac{1}{2}

, 9.

\frac{5}{6}

, 10.

2 \frac{2}{3}

, 11.

2 \frac{1}{3}

1 \frac{1}{24} + \frac{9}{24} =

\frac{4}{5}

, 2.

\frac{1}{4}

, 3.

1 \frac{1}{2}

, 4.

2 \frac{1}{3}

, 5.

1

, 6.

1 \frac{5}{12}

, 7.

2 \frac{1}{6}

, 8.

\frac{1}{2}

, 9.

\frac{5}{6}

, 10.

2 \frac{2}{3}

, 11.

2 \frac{1}{3}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RQXiSs9ltStJD

Ćwiczenie 14

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

ROIDIq4Re7wKS

Ćwiczenie 15

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 16

Zastanów się, jakimi liczbami różnymi od zera można uzupełnić liczniki ułamków w podanych przykładach. Ile wynosi ich suma? Na ile sposobów można uzupełnić brakujące liczniki?

$\frac{\dots}{8} + \frac{\dots}{8} = 1 \frac{1}{4}$
$\frac{\dots}{8} + \frac{\dots}{8} = 1 \frac{3}{4}$
$\frac{\dots}{8} + \frac{\dots}{8} = \frac{1}{2}$
$\frac{\dots}{6} + \frac{\dots}{6} = 2 \frac{1}{3}$
$\frac{\dots}{12} + 1 \frac{\dots}{12} = 2 \frac{2}{3}$
$6 \frac{\dots}{9} + 3 \frac{\dots}{9} = 10 \frac{2}{3}$

R1MnthFqg19uA

Uzupełnij luki, wpisując prawidłowe liczby. Suma liczników w działaniu

\frac{\dots}{8} + \frac{\dots}{8} = 1 \frac{1}{4}

jest równa Tu uzupełnij. Liczniki w tym działaniu można uzupełnić na Tu uzupełnij sposobów.Suma liczników w działaniu

\frac{\dots}{8} + \frac{\dots}{8} = 1 \frac{3}{4}

jest równa Tu uzupełnij. Liczniki w tym działaniu można uzupełnić na Tu uzupełnij sposobów.Suma liczników w działaniu

\frac{\dots}{8} + \frac{\dots}{8} = \frac{1}{2}

jest równa Tu uzupełnij. Liczniki w tym działaniu można uzupełnić na Tu uzupełnij sposoby.Suma liczników w działaniu

\frac{\dots}{6} + \frac{\dots}{6} = 2 \frac{1}{3}

jest równa Tu uzupełnij. Liczniki w tym działaniu można uzupełnić na Tu uzupełnij sposobów.Suma liczników w działaniu

\frac{\dots}{12} + 1 \frac{\dots}{12} = 2 \frac{2}{3}

jest równa Tu uzupełnij. Liczniki w tym działaniu można uzupełnić na Tu uzupełnij sposobów.Suma liczników w działaniu

6 \frac{\dots}{9} + 3 \frac{\dots}{9} = 10 \frac{2}{3}

jest równa Tu uzupełnij. Liczniki w tym działaniu można uzupełnić na Tu uzupełnij sposobów.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 17

Zapoznaj się z poniższymi rysunkami. Jaka część figury nie została zamalowana?

R1BX5ZVf4WDhb1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RLDHssziFGK9n1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R10nniWnqoyNt

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 18

Zapisz odejmowanie ilustrujące sytuację przedstawioną na rysunkach. Przeciągnij i upuść liczby w odpowiednie miejsca na grafikach.

RR8CUWc4rwDxB

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1NtJQ1fzSt8P

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1Up83IPn4Pef

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RJRgcREfdGZp0

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rwfs7DSJXWnTQ

Połącz w pary opisy grafik z różnicami, które one opisują. Na ilustracji przedstawione jest pewne odejmowanie. Narysowane są trzy prostokąty, z czego ostatni podzielony jest na 5 kwadratów równej wielkości. Pierwsze dwa prostokąty są zamalowane i zamalowane są cztery części trzeciego prostokąta. Narysowany jest znak minus, a za nim znajdują się dwa prostokąty, z czego drugi podzielony jest na 5 kwadratów równej wielkości. Zamalowany jest pierwszy prostokąt oraz trzy części drugiego prostokąta. Po znaku równości znajdują się dwa prostokąty, z czego drugi podzielony jest na 5 kwadratów równej wielkości. Zamalowany jest pierwszy prostokąt oraz jedna część drugiego prostokąta. Możliwe odpowiedzi: 1.

2 \frac{4}{5} - 1 \frac{3}{5} = 1 \frac{1}{5}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 19

R1cYFrNyVcHPo

Oblicz podane różnice, a następnie uzupełnij równości, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.

3 \frac{1}{7} - 1 \frac{3}{7} =

3 \frac{5}{8}

, 2.

2 \frac{7}{9}

, 3.

\frac{4}{7}

, 4.

\frac{8}{13}

, 5.

2 \frac{9}{11}

, 6.

9 \frac{9}{13}

, 7.

\frac{8}{11}

, 8.

1 \frac{4}{5}

, 9.

\frac{11}{15}

, 10.

5 \frac{2}{5}

, 11.

4 \frac{2}{3}

, 12.

6 \frac{3}{10}

, 13.

4 \frac{3}{4}

, 14.

1 \frac{5}{7}

, 15.

\frac{5}{9}

, 16.

1 \frac{3}{4}

, 17.

\frac{11}{12}

5 \frac{1}{4} - \frac{2}{4} =

3 \frac{5}{8}

, 2.

2 \frac{7}{9}

, 3.

\frac{4}{7}

, 4.

\frac{8}{13}

, 5.

2 \frac{9}{11}

, 6.

9 \frac{9}{13}

, 7.

\frac{8}{11}

, 8.

1 \frac{4}{5}

, 9.

\frac{11}{15}

, 10.

5 \frac{2}{5}

, 11.

4 \frac{2}{3}

, 12.

6 \frac{3}{10}

, 13.

4 \frac{3}{4}

, 14.

1 \frac{5}{7}

, 15.

\frac{5}{9}

, 16.

1 \frac{3}{4}

, 17.

\frac{11}{12}

5 \frac{2}{9} - 2 \frac{4}{9} =

3 \frac{5}{8}

, 2.

2 \frac{7}{9}

, 3.

\frac{4}{7}

, 4.

\frac{8}{13}

, 5.

2 \frac{9}{11}

, 6.

9 \frac{9}{13}

, 7.

\frac{8}{11}

, 8.

1 \frac{4}{5}

, 9.

\frac{11}{15}

, 10.

5 \frac{2}{5}

, 11.

4 \frac{2}{3}

, 12.

6 \frac{3}{10}

, 13.

4 \frac{3}{4}

, 14.

1 \frac{5}{7}

, 15.

\frac{5}{9}

, 16.

1 \frac{3}{4}

, 17.

\frac{11}{12}

4 \frac{3}{8} - \frac{6}{8} =

3 \frac{5}{8}

, 2.

2 \frac{7}{9}

, 3.

\frac{4}{7}

, 4.

\frac{8}{13}

, 5.

2 \frac{9}{11}

, 6.

9 \frac{9}{13}

, 7.

\frac{8}{11}

, 8.

1 \frac{4}{5}

, 9.

\frac{11}{15}

, 10.

5 \frac{2}{5}

, 11.

4 \frac{2}{3}

, 12.

6 \frac{3}{10}

, 13.

4 \frac{3}{4}

, 14.

1 \frac{5}{7}

, 15.

\frac{5}{9}

, 16.

1 \frac{3}{4}

, 17.

\frac{11}{12}

2 \frac{2}{5} - \frac{3}{5} =

3 \frac{5}{8}

, 2.

2 \frac{7}{9}

, 3.

\frac{4}{7}

, 4.

\frac{8}{13}

, 5.

2 \frac{9}{11}

, 6.

9 \frac{9}{13}

, 7.

\frac{8}{11}

, 8.

1 \frac{4}{5}

, 9.

\frac{11}{15}

, 10.

5 \frac{2}{5}

, 11.

4 \frac{2}{3}

, 12.

6 \frac{3}{10}

, 13.

4 \frac{3}{4}

, 14.

1 \frac{5}{7}

, 15.

\frac{5}{9}

, 16.

1 \frac{3}{4}

, 17.

\frac{11}{12}

12 \frac{1}{13} - 2 \frac{5}{13} =

3 \frac{5}{8}

, 2.

2 \frac{7}{9}

, 3.

\frac{4}{7}

, 4.

\frac{8}{13}

, 5.

2 \frac{9}{11}

, 6.

9 \frac{9}{13}

, 7.

\frac{8}{11}

, 8.

1 \frac{4}{5}

, 9.

\frac{11}{15}

, 10.

5 \frac{2}{5}

, 11.

4 \frac{2}{3}

, 12.

6 \frac{3}{10}

, 13.

4 \frac{3}{4}

, 14.

1 \frac{5}{7}

, 15.

\frac{5}{9}

, 16.

1 \frac{3}{4}

, 17.

\frac{11}{12}

8 \frac{1}{3} - 3 \frac{2}{3} =

3 \frac{5}{8}

, 2.

2 \frac{7}{9}

, 3.

\frac{4}{7}

, 4.

\frac{8}{13}

, 5.

2 \frac{9}{11}

, 6.

9 \frac{9}{13}

, 7.

\frac{8}{11}

, 8.

1 \frac{4}{5}

, 9.

\frac{11}{15}

, 10.

5 \frac{2}{5}

, 11.

4 \frac{2}{3}

, 12.

6 \frac{3}{10}

, 13.

4 \frac{3}{4}

, 14.

1 \frac{5}{7}

, 15.

\frac{5}{9}

, 16.

1 \frac{3}{4}

, 17.

\frac{11}{12}

12 \frac{2}{10} - 5 \frac{9}{10} =

3 \frac{5}{8}

, 2.

2 \frac{7}{9}

, 3.

\frac{4}{7}

, 4.

\frac{8}{13}

, 5.

2 \frac{9}{11}

, 6.

9 \frac{9}{13}

, 7.

\frac{8}{11}

, 8.

1 \frac{4}{5}

, 9.

\frac{11}{15}

, 10.

5 \frac{2}{5}

, 11.

4 \frac{2}{3}

, 12.

6 \frac{3}{10}

, 13.

4 \frac{3}{4}

, 14.

1 \frac{5}{7}

, 15.

\frac{5}{9}

, 16.

1 \frac{3}{4}

, 17.

\frac{11}{12}

1 \frac{7}{11} - \frac{10}{11} =

3 \frac{5}{8}

, 2.

2 \frac{7}{9}

, 3.

\frac{4}{7}

, 4.

\frac{8}{13}

, 5.

2 \frac{9}{11}

, 6.

9 \frac{9}{13}

, 7.

\frac{8}{11}

, 8.

1 \frac{4}{5}

, 9.

\frac{11}{15}

, 10.

5 \frac{2}{5}

, 11.

4 \frac{2}{3}

, 12.

6 \frac{3}{10}

, 13.

4 \frac{3}{4}

, 14.

1 \frac{5}{7}

, 15.

\frac{5}{9}

, 16.

1 \frac{3}{4}

, 17.

\frac{11}{12}

13 \frac{9}{12} - 12 \frac{10}{12} =

3 \frac{5}{8}

, 2.

2 \frac{7}{9}

, 3.

\frac{4}{7}

, 4.

\frac{8}{13}

, 5.

2 \frac{9}{11}

, 6.

9 \frac{9}{13}

, 7.

\frac{8}{11}

, 8.

1 \frac{4}{5}

, 9.

\frac{11}{15}

, 10.

5 \frac{2}{5}

, 11.

4 \frac{2}{3}

, 12.

6 \frac{3}{10}

, 13.

4 \frac{3}{4}

, 14.

1 \frac{5}{7}

, 15.

\frac{5}{9}

, 16.

1 \frac{3}{4}

, 17.

\frac{11}{12}

4 \frac{7}{15} - 3 \frac{11}{15} =

3 \frac{5}{8}

, 2.

2 \frac{7}{9}

, 3.

\frac{4}{7}

, 4.

\frac{8}{13}

, 5.

2 \frac{9}{11}

, 6.

9 \frac{9}{13}

, 7.

\frac{8}{11}

, 8.

1 \frac{4}{5}

, 9.

\frac{11}{15}

, 10.

5 \frac{2}{5}

, 11.

4 \frac{2}{3}

, 12.

6 \frac{3}{10}

, 13.

4 \frac{3}{4}

, 14.

1 \frac{5}{7}

, 15.

\frac{5}{9}

, 16.

1 \frac{3}{4}

, 17.

\frac{11}{12}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 20

Zastanów się co można powiedzieć o licznikach w każdym z podpunktów.

$\frac{□}{8} - \frac{□}{8} = 1 \frac{1}{4}$
$\frac{□}{8} - \frac{□}{8} = 1 \frac{3}{4}$
$\frac{□}{8} - \frac{□}{8} = \frac{1}{2}$
$\frac{□}{6} - \frac{□}{6} = 2 \frac{1}{3}$

RJASOnh8zXkxV

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RQEHzvcE1U0fo

Ćwiczenie 21

Oblicz, a następnie uzupełnij luki odpowiednimi liczbami. Kliknij w lukę, aby rozwinąć listę i wybierz brakującą liczbę dla każdej równości.

4 + 1 \frac{1}{5} =

6 \frac{1}{3}

, 2.

6 \frac{1}{2}

, 3.

5 \frac{1}{5}

, 4.

1 \frac{2}{3}

, 5.

5 \frac{1}{4}

, 6.

1 \frac{2}{3}

, 7.

1 \frac{3}{4}

, 8.

\frac{5}{6}

, 9.

6 \frac{5}{13}

, 10.

1 \frac{5}{6}

, 11.

13 \frac{4}{5}

, 12.

5 \frac{1}{2}

1 \frac{5}{8} + 3 \frac{7}{8} =

6 \frac{1}{3}

, 2.

6 \frac{1}{2}

, 3.

5 \frac{1}{5}

, 4.

1 \frac{2}{3}

, 5.

5 \frac{1}{4}

, 6.

1 \frac{2}{3}

, 7.

1 \frac{3}{4}

, 8.

\frac{5}{6}

, 9.

6 \frac{5}{13}

, 10.

1 \frac{5}{6}

, 11.

13 \frac{4}{5}

, 12.

5 \frac{1}{2}

6 \frac{11}{15} + 7 \frac{1}{15} =

6 \frac{1}{3}

, 2.

6 \frac{1}{2}

, 3.

5 \frac{1}{5}

, 4.

1 \frac{2}{3}

, 5.

5 \frac{1}{4}

, 6.

1 \frac{2}{3}

, 7.

1 \frac{3}{4}

, 8.

\frac{5}{6}

, 9.

6 \frac{5}{13}

, 10.

1 \frac{5}{6}

, 11.

13 \frac{4}{5}

, 12.

5 \frac{1}{2}

2 \frac{5}{12} + \frac{11}{12} + 3 \frac{2}{12} =

6 \frac{1}{3}

, 2.

6 \frac{1}{2}

, 3.

5 \frac{1}{5}

, 4.

1 \frac{2}{3}

, 5.

5 \frac{1}{4}

, 6.

1 \frac{2}{3}

, 7.

1 \frac{3}{4}

, 8.

\frac{5}{6}

, 9.

6 \frac{5}{13}

, 10.

1 \frac{5}{6}

, 11.

13 \frac{4}{5}

, 12.

5 \frac{1}{2}

7 - \frac{8}{13} =

6 \frac{1}{3}

, 2.

6 \frac{1}{2}

, 3.

5 \frac{1}{5}

, 4.

1 \frac{2}{3}

, 5.

5 \frac{1}{4}

, 6.

1 \frac{2}{3}

, 7.

1 \frac{3}{4}

, 8.

\frac{5}{6}

, 9.

6 \frac{5}{13}

, 10.

1 \frac{5}{6}

, 11.

13 \frac{4}{5}

, 12.

5 \frac{1}{2}

4 - 2 \frac{1}{3} =

6 \frac{1}{3}

, 2.

6 \frac{1}{2}

, 3.

5 \frac{1}{5}

, 4.

1 \frac{2}{3}

, 5.

5 \frac{1}{4}

, 6.

1 \frac{2}{3}

, 7.

1 \frac{3}{4}

, 8.

\frac{5}{6}

, 9.

6 \frac{5}{13}

, 10.

1 \frac{5}{6}

, 11.

13 \frac{4}{5}

, 12.

5 \frac{1}{2}

3 \frac{5}{6} - 2 \frac{1}{6} =

6 \frac{1}{3}

, 2.

6 \frac{1}{2}

, 3.

5 \frac{1}{5}

, 4.

1 \frac{2}{3}

, 5.

5 \frac{1}{4}

, 6.

1 \frac{2}{3}

, 7.

1 \frac{3}{4}

, 8.

\frac{5}{6}

, 9.

6 \frac{5}{13}

, 10.

1 \frac{5}{6}

, 11.

13 \frac{4}{5}

, 12.

5 \frac{1}{2}

5 \frac{3}{20} - 3 \frac{8}{20} =

6 \frac{1}{3}

, 2.

6 \frac{1}{2}

, 3.

5 \frac{1}{5}

, 4.

1 \frac{2}{3}

, 5.

5 \frac{1}{4}

, 6.

1 \frac{2}{3}

, 7.

1 \frac{3}{4}

, 8.

\frac{5}{6}

, 9.

6 \frac{5}{13}

, 10.

1 \frac{5}{6}

, 11.

13 \frac{4}{5}

, 12.

5 \frac{1}{2}

13 \frac{7}{24} - 12 \frac{11}{24} =

6 \frac{1}{3}

, 2.

6 \frac{1}{2}

, 3.

5 \frac{1}{5}

, 4.

1 \frac{2}{3}

, 5.

5 \frac{1}{4}

, 6.

1 \frac{2}{3}

, 7.

1 \frac{3}{4}

, 8.

\frac{5}{6}

, 9.

6 \frac{5}{13}

, 10.

1 \frac{5}{6}

, 11.

13 \frac{4}{5}

, 12.

5 \frac{1}{2}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R13Cu7Yoq7oxH

Ćwiczenie 22

Oblicz, pamiętając o kolejności wykonywania działań, a następnie uzupełnij luki odpowiednimi liczbami. Kliknij w lukę, aby rozwinąć listę i wybierz brakującą liczbę dla każdej równości.

2 \frac{5}{9} + 3 \frac{7}{9} - 4 \frac{8}{9} =

1 \frac{1}{9}

, 2.

1 \frac{5}{6}

, 3.

1 \frac{4}{9}

, 4.

\frac{5}{6}

, 5.

\frac{3}{4}

, 6.

1 \frac{3}{4}

, 7.

1 \frac{2}{3}

7 \frac{5}{6} - 5 \frac{2}{6} - 1 \frac{4}{6} =

1 \frac{1}{9}

, 2.

1 \frac{5}{6}

, 3.

1 \frac{4}{9}

, 4.

\frac{5}{6}

, 5.

\frac{3}{4}

, 6.

1 \frac{3}{4}

, 7.

1 \frac{2}{3}

9 \frac{1}{8} - (2 \frac{7}{8} + 4 \frac{4}{8}) =

1 \frac{1}{9}

, 2.

1 \frac{5}{6}

, 3.

1 \frac{4}{9}

, 4.

\frac{5}{6}

, 5.

\frac{3}{4}

, 6.

1 \frac{3}{4}

, 7.

1 \frac{2}{3}

5 \frac{6}{12} - (5 \frac{1}{12} - 1 \frac{5}{12}) =

1 \frac{1}{9}

, 2.

1 \frac{5}{6}

, 3.

1 \frac{4}{9}

, 4.

\frac{5}{6}

, 5.

\frac{3}{4}

, 6.

1 \frac{3}{4}

, 7.

1 \frac{2}{3}

12 - (16 \frac{7}{18} - 5 \frac{9}{18}) =

1 \frac{1}{9}

, 2.

1 \frac{5}{6}

, 3.

1 \frac{4}{9}

, 4.

\frac{5}{6}

, 5.

\frac{3}{4}

, 6.

1 \frac{3}{4}

, 7.

1 \frac{2}{3}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RztE3pwld8qd9

Ćwiczenie 23

Oblicz, a następnie uzupełnij luki odpowiednimi liczbami. Kliknij w lukę, aby rozwinąć listę i wybierz brakującą liczbę dla każdej odpowiedzi. Do sumy liczb

6 \frac{7}{15}

2 \frac{1}{15}

dodano sumę liczb

3 \frac{5}{15}

1 \frac{11}{15}

.
Odpowiedź: Wynik tego działania to 1.

12 \frac{3}{5}

, 2.

8 \frac{5}{12}

, 3.

9 \frac{5}{12}

, 4.

4 \frac{2}{3}

, 5.

4 \frac{1}{3}

, 6.

13 \frac{3}{5}

.Od sumy liczb

4 \frac{3}{12}

2 \frac{1}{12}

odjęto różnicę liczb

12 \frac{5}{12}

10 \frac{9}{12}

.
Odpowiedź: Wynik tego działania to 1.

12 \frac{3}{5}

, 2.

8 \frac{5}{12}

, 3.

9 \frac{5}{12}

, 4.

4 \frac{2}{3}

, 5.

4 \frac{1}{3}

, 6.

13 \frac{3}{5}

.Do sumy liczb

4 \frac{5}{24}

3 \frac{7}{24}

dodano ich różnicę.
Odpowiedź: Wynik tego działania to 1.

12 \frac{3}{5}

, 2.

8 \frac{5}{12}

, 3.

9 \frac{5}{12}

, 4.

4 \frac{2}{3}

, 5.

4 \frac{1}{3}

, 6.

13 \frac{3}{5}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R9Johls65NtTU1

Ćwiczenie 24

Tato kupił taśmę do uszczelniania okien. Do pierwszego okna zużył $7 \frac{3}{8} m$ , do drugiego $9 \frac{1}{8} m$ , a do trzeciego $8 \frac{6}{8} m$ . Ile metrów taśmy zostało, jeśli w krążku były początkowo $33$ metry?

$7 \frac{3}{5}$ , $7 \frac{2}{3}$ , $7 \frac{4}{5}$ , $7 \frac{3}{4}$

Odp.: Zostało ............ m taśmy.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1dRWx35HQNHa1

Ćwiczenie 25

Ze słoja, w którym było $7 \frac{1}{4} kg$ miodu, pszczelarz najpierw odlał $2 \frac{3}{4} kg$ , a następnie dolał $1 \frac{1}{4} kg$ . Ile miodu jest w słoju?

$5 \frac{2}{3}$ , $5 \frac{3}{4}$ , $5 \frac{3}{5}$ , $5 \frac{4}{5}$

Odp.: W słoju jest teraz ............ $kg$ miodu.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rm2J7kW5LAmVt1

Ćwiczenie 26

Janek bardzo lubi czytać książki i oglądać filmy. Czytanie zajmuje mu codziennie

1 \frac{2}{3}

godziny. Na filmy przeznacza o

1 \frac{1}{3}

godziny więcej. Ile czasu zajmują mu każdego dnia te dwie czynności?
Uzupełnij poniższą lukę. Kliknij w nią, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. Odpowiedź: Na czytanie i oglądanie filmów Janek przeznacza codziennie 1.

4 \frac{3}{4}

, 2.

4 \frac{1}{3}

, 3.

4 \frac{1}{4}

, 4.

4 \frac{2}{3}

godziny.

Janek bardzo lubi czytać książki i oglądać filmy. Czytanie zajmuje mu codziennie $1 \frac{2}{3} h$ godziny. Na filmy przeznacza o $1 \frac{1}{3} h$ więcej. Ile czasu zajmują mu każdego dnia te dwie czynności?

$4 \frac{1}{3}$ , $4 \frac{2}{3}$ , $4 \frac{1}{4}$ , $4 \frac{3}{4}$

Odp.: Na czytanie i oglądanie filmów Janek przeznacza codziennie ............ $h$ .

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R141k3YGxBPVf1

Ćwiczenie 27

Do dziesięciolitrowego słoja, w którym było $1 \frac{4}{5}$ litra soku, mama dolała $1 \frac{3}{5}$ litra soku. Ile mogłaby jeszcze dolać, aby napełnić słój do połowy?

$1 \frac{2}{5}$ , $1 \frac{3}{5}$ , $1 \frac{1}{5}$ , $1 \frac{4}{5}$

Odp.: Mama mogłaby dolać ............ litra soku.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 28

Przepisz do zeszytu poniższe równości i uzupełnij je tak, aby były prawdziwe. Brakujące liczby wybierz spośród: $\frac{1}{11}$ , $\frac{3}{11}$ , $\frac{4}{11}$ , $\frac{5}{11}$ , $3 \frac{8}{11}$ , $\frac{7}{11}$ , $\frac{9}{11}$ , $2 \frac{3}{11}$ .

$\dots + \dots + \dots + \dots = 2$
$\dots + \dots + \dots + \dots = 3$
$\dots - \dots - \dots - \dots = 2$

$\frac{9}{11} + \frac{7}{11} + \frac{5}{11} + \frac{1}{11} = 2$
$2 \frac{3}{11} + \frac{4}{11} + \frac{1}{11} + \frac{3}{11} = 3$
$3 \frac{8}{11} - \frac{9}{11} - \frac{5}{11} - \frac{5}{11} = 2$

RiHrCLeywI1yr1

Ćwiczenie 29

Mama kupiła $1 \frac{1}{2} kg$ pomarańczy, $2 kg$ ziemniaków i $\frac{1}{2} kg$ pomidorów. Ile ważyły te zakupy?

Zakupy ważyły ............ kg.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R102MCxLWcdlM

Ćwiczenie 30

Wczoraj Bartek spędził w szkole

\frac{7}{24}

doby, a spał przez

\frac{10}{24}

doby. Jaką część doby Bartek mógł maksymalnie przeznaczyć na inne swoje działania? Ile to godzin? Uzupełnij odpowiedź, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Odpowiedź: Jest to 1.

7

, 2.

\frac{5}{24}

, 3.

\frac{8}{24}

, 4.

5

, 5.

\frac{7}{24}

, 6.

8

, 7.

6

, 8.

\frac{6}{24}

doby, czyli 1.

7

, 2.

\frac{5}{24}

, 3.

\frac{8}{24}

, 4.

5

, 5.

\frac{7}{24}

, 6.

8

, 7.

6

, 8.

\frac{6}{24}

h

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 31

W tradycyjnym kolejowym wagonie osobowym jest $10$ przedziałów. W każdym przedziale wagonu drugiej klasy znajduje się $8$ miejsc do siedzenia. Na wycieczkę pojechało pociągiem $25$ uczniów z klasy $4 a$ oraz $28$ uczniów z klasy $4 b$ . Z każdą klasą pojechało dwóch opiekunów. Wszyscy zajęli miejsca siedzące w tym samym wagonie drugiej klasy.

R1TzIKgQj0dQL

Uzupełnij odpowiedzi na poniższe pytania, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Jaką część wszystkich miejsc w wagonie zajęli uczniowie klasy

4 a

, uczniowie klasy

4 b

i opiekunowie obu klas? Oblicz, jaką część miejsc zajęli wszyscy uczestnicy wycieczki.

Odpowiedź: Uczniowie klasy

4 a

zajęli 1.

\frac{23}{80}

, 2.

\frac{28}{80}

, 3.

\frac{57}{80}

, 4.

\frac{4}{80}

, 5.

\frac{2}{80}

, 6.

\frac{30}{80}

, 7.

\frac{27}{80}

, 8.

\frac{25}{80}

wszystkich miejsc, uczniowie klasy

4 b

zajęli 1.

\frac{23}{80}

, 2.

\frac{28}{80}

, 3.

\frac{57}{80}

, 4.

\frac{4}{80}

, 5.

\frac{2}{80}

, 6.

\frac{30}{80}

, 7.

\frac{27}{80}

, 8.

\frac{25}{80}

, a opiekunowie obu klas zajęli 1.

\frac{23}{80}

, 2.

\frac{28}{80}

, 3.

\frac{57}{80}

, 4.

\frac{4}{80}

, 5.

\frac{2}{80}

, 6.

\frac{30}{80}

, 7.

\frac{27}{80}

, 8.

\frac{25}{80}

wszystkich miejsc. Łącznie wszyscy uczestnicy wycieczki zajęli 1.

\frac{23}{80}

, 2.

\frac{28}{80}

, 3.

\frac{57}{80}

, 4.

\frac{4}{80}

, 5.

\frac{2}{80}

, 6.

\frac{30}{80}

, 7.

\frac{27}{80}

, 8.

\frac{25}{80}

wszystkich miejsc.
Oblicz, jaką część miejsc w wagonie mieli do dyspozycji pozostali pasażerowie.

Odpowiedź: Pozostali pasażerowie mieli do dyspozycji 1.

\frac{23}{80}

, 2.

\frac{28}{80}

, 3.

\frac{57}{80}

, 4.

\frac{4}{80}

, 5.

\frac{2}{80}

, 6.

\frac{30}{80}

, 7.

\frac{27}{80}

, 8.

\frac{25}{80}

wszystkich miejsc.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1Xv4tENOyfDU

Ćwiczenie 32

$13 \frac{9}{10} km$
$11 \frac{1}{10} km$
$8 \frac{2}{10} km$
$16 \frac{1}{10} km$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 33

Kasia kupiła tabliczkę swojej ulubionej czekolady. Postanowiła przez trzy pierwsze dni tygodnia zjeść $\frac{6}{24}$ tabliczki, w czwartek i piątek również $\frac{6}{24}$ , a w sobotę i niedzielę $\frac{8}{24}$ czekolady.

Rb9WLAZV1LeVj1

Rysunek dziewczynki, która w ręku trzyma czekoladę podzieloną na 24 kawałki. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R7EVm8mnW7Lnw

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1bzlveeHhes81

Ćwiczenie 34

Janek był wczoraj w szkole przez

6 \frac{1}{4} h

. Potem przez

\frac{3}{4} h

wracał spacerkiem do domu. Zjedzenie obiadu i relaks przy czytaniu książki zajęły mu

1 \frac{3}{4} h

. Po odpoczynku Jacek wyszedł na trening. Wykonaj obliczenia i uzupełnij poniższe zdania, wpisując w luki odpowiednie liczby. Pobyt w szkole i powrót do domu zajął Jackowi Tu uzupełnij

h

. Jeżeli Jacek przebywał w szkole od godziny

7 : 50

, to na trening wyszedł o godzinie Tu uzupełnij:Tu uzupełnij.

Janek był wczoraj w szkole przez $6 \frac{1}{4} h$ . Potem przez $\frac{3}{4} h$ wracał spacerkiem do domu. Zjedzenie obiadu i relaks przy czytaniu książki zajęły mu $1 \frac{3}{4} h$ . Po odpoczynku Jacek wyszedł na trening. Wykonaj obliczenia i uzupełnij.

a) Pobyt w szkole i powrót do domu zajął Jackowi ............ $h$ .
b) Jeżeli Jacek przebywał w szkole od godziny $7 : 50$ , to na trening wyszedł o godzinie ............: .............

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1bFG32vbJDCI

Ćwiczenie 35

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R2pq7XobtgcdK

Ćwiczenie 36

$5 \frac{3}{5} cm$
$16 cm$
$11 \frac{1}{5} cm$
$32 cm$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 37

Najkrótszy bok pięciokąta $A B C D E$ ma długość $2 \frac{9}{10} cm$ . Każdy kolejny bok jest o $1 \frac{3}{10} cm$ dłuższy od poprzedniego. Oblicz długość tej łamanej zamkniętej.

R1NzFBiK1QHu51

Rysunek łamanej zamkniętej A B C D E, która składa się z pięciu odcinków. Odcinek AB ma długość dwie całe i dziewięć dziesiątych centymetra. Każdy kolejny odcinek jest coraz dłuższy. Koniec ostatniego odcinka jest początkiem pierwszego odcinka. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1Gsp9uvFcSVm

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 38

Obwód prostokąta $A B C D$ jest o $10 cm$ dłuższy od obwodu prostokąta $A P R D$ .

Długość odcinka $B C$ wynosi $3 \frac{1}{4} cm$ . Oblicz obwód prostokąta $P B C R$ .

R1WphDGdmraCx1

Rysunek prostokąta A B C D i prostokąta A P R D. Bok BC jest równoległy do boku PR. Odcinek CB ma długość trzy całe i jedna czwarta centymetra. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R17FEDOXdIctv

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

2. Dodawanie i odejmowanie ułamków o różnych mianownikach

Działania na ułamkach zwykłych