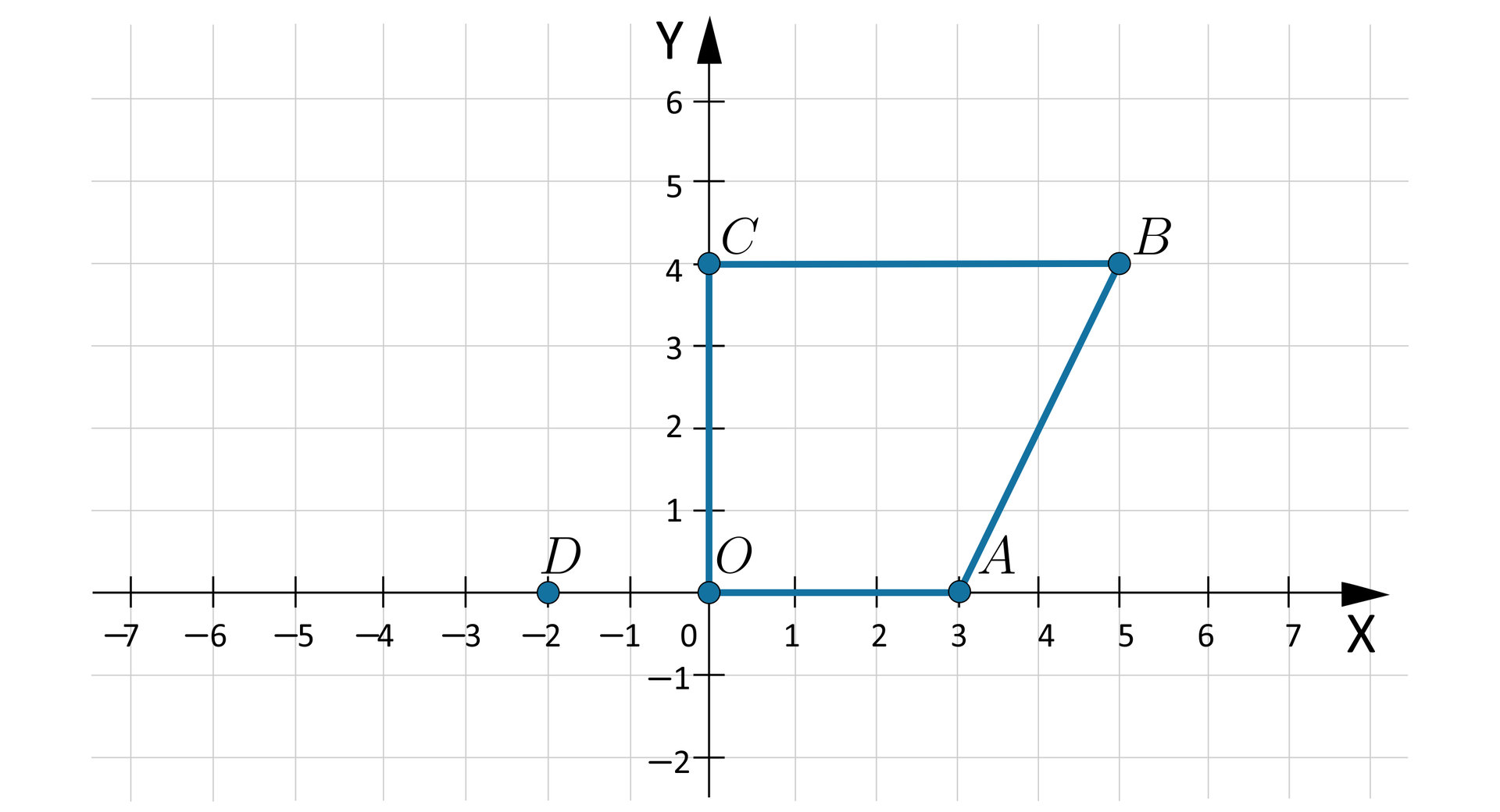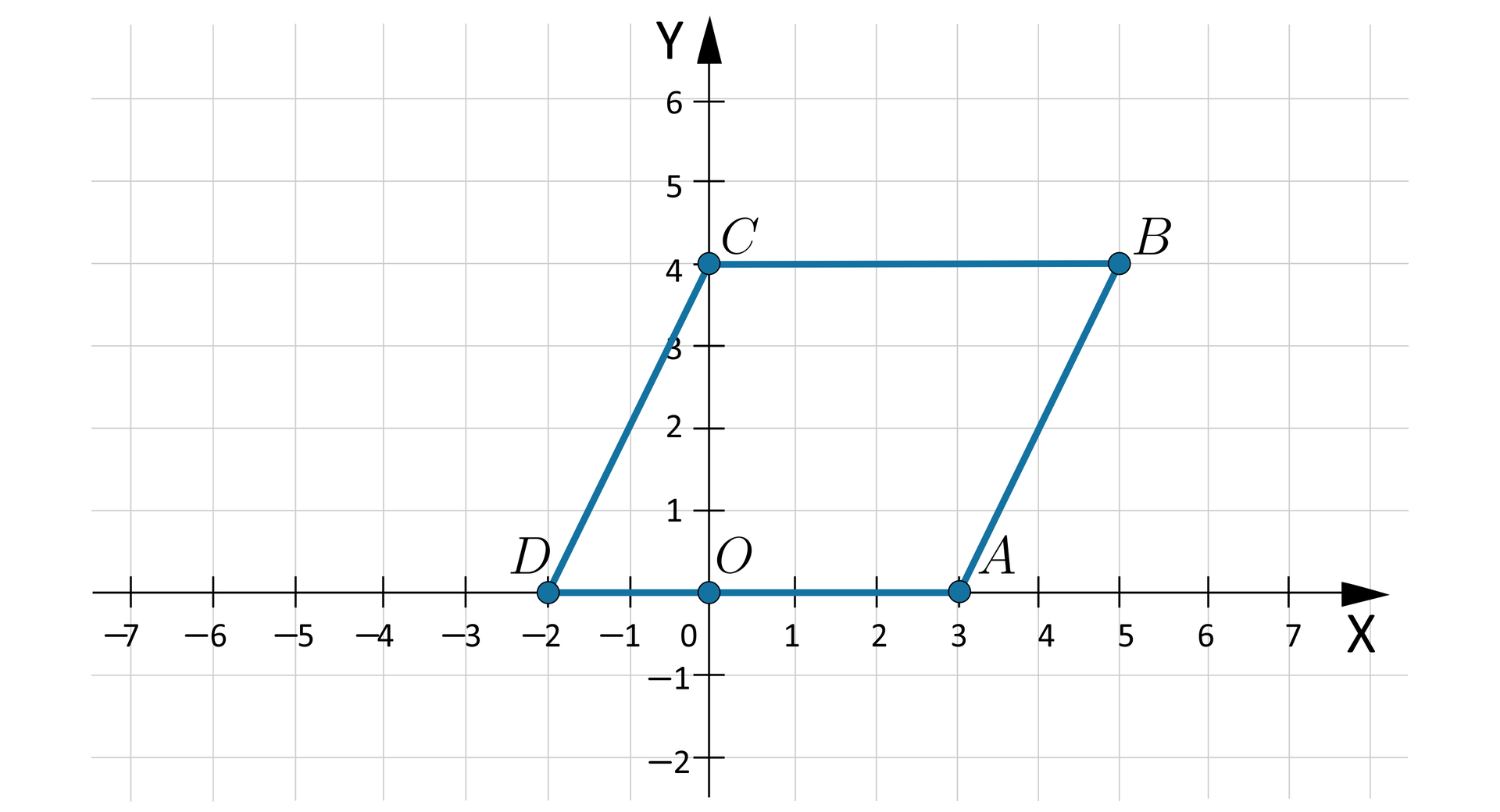Układ współrzędnych
5. Wielokąty w układzie współrzędnych
W praktyce, chcąc przejść z jednego miejsca do drugiego, rzadko poruszamy się po trasie, jaką wyznaczylibyśmy na planie jako najkrótszą. Na drodze bowiem znajdują się różne przeszkody, np. domy, jeziora, itp. Schemat ulic w miastach często przypomina kratownicę. Najkrótsza odległość w mieście będzie więc nieco inna niż ta teoretyczna, wykorzystywana na lekcjach geometrii.
W tym przypadku do obliczenia odległości posługujemy się tzw. metryką miejską. W tej metryce najkrótsza droga między dwoma punktami to suma wartości bezwzględnych różnic współrzędnych punktu początkowego i końcowego.
Znasz już podstawowe własności figur płaskich. W tym materiale przypomnisz sobie, że umieszczenie takich figur w układzie współrzędnych stwarza możliwość wskazania współrzędnych ich wierzchołków oraz innych punktów charakterystycznych.
Odległość punktów na osi liczbowej
Odległością punktów i , zaznaczonych na osi liczbowej, jest długość odcinka .
Długość ta jest równa wartości bezwzględnej różnicy współrzędnych punktów i .

![Rysunki trzech osi liczbowych z zaznaczonymi liczbami całkowitymi od -5 do 5. Odcinek jednostkowy równy jest 1. Na pierwszej osi zaznaczone punkty o współrzędnych A =(-1) i M =(3). Zapis: wartość bezwzględna AM = wartość bezwzględna [3 -( -1)] =4. Na drugiej osi zaznaczone punkty o współrzędnych Z =(0) i W =(4). Zapis: wartość bezwzględna WZ = wartość bezwzględna (0 -4) =4. Na trzeciej osi zaznaczone punkty o współrzędnych R =(-2), S =(2). Zapis: wartość bezwzględna SR = wartość bezwzględna (-2 -2) =4.](https://static.zpe.gov.pl/portal/f/res-minimized/R1WtSnpofLYix/1668787680/1vNARXcGFzRylrNdmjQ0lwWwM79aAKSG.png)
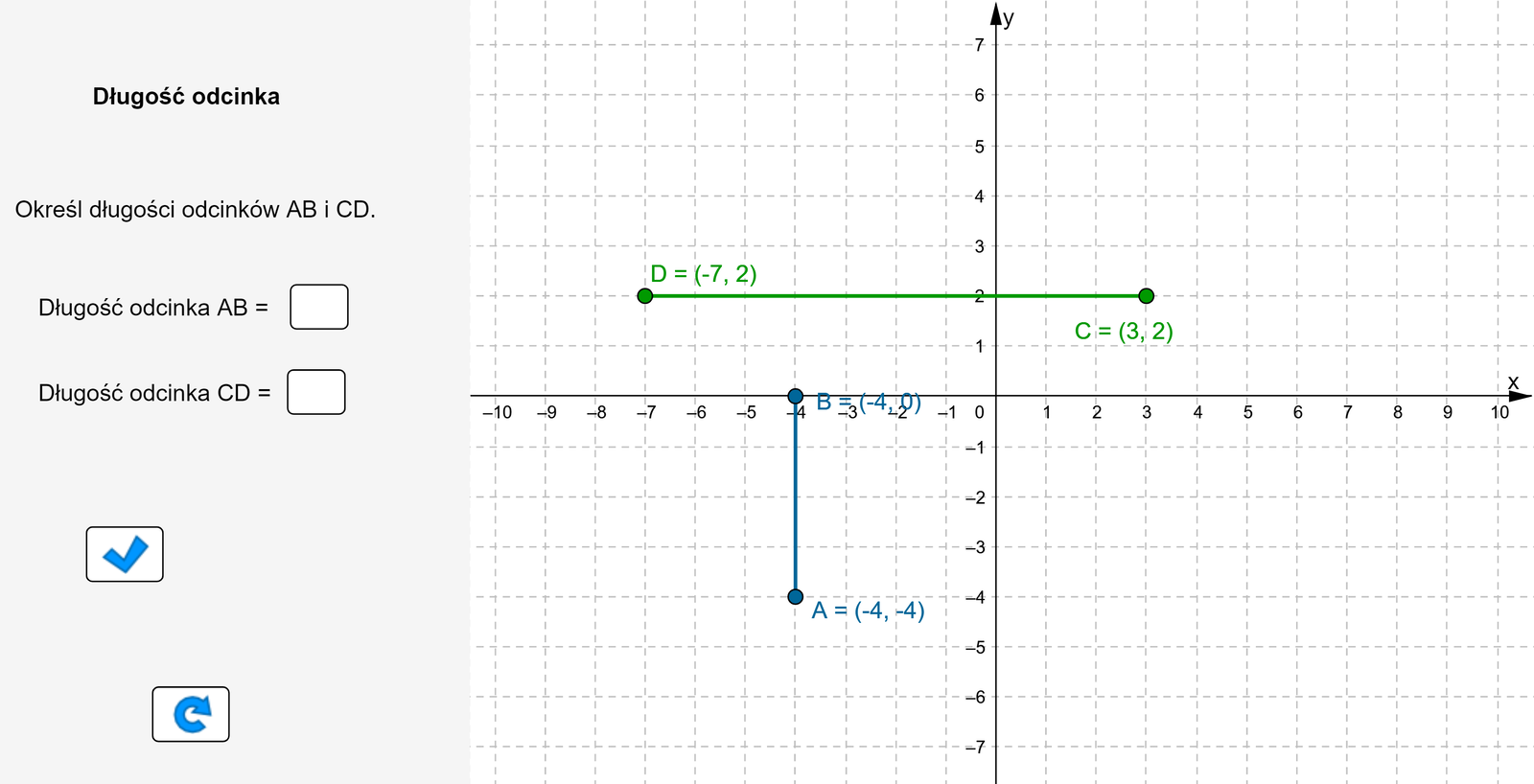
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Własności odległości punktów.
Jeśli , , są dowolnymi punktami na płaszczyźnie, to
oraz wtedy i tylko wtedy, gdy ,
,
.
Odcinek w układzie współrzędnych
W przypadku, gdy odcinek leży w układzie współrzędnych na jednej z osi liczbowych, jego długość jest równa odległości punktów i .
![Rysunek układu współrzędnych z zaznaczonymi odcinkami AB i CD, którego końce wyznaczają punkty o współrzędnych A =(0, 3), B =(0, -2), R =(-6, 0), W =(-3, 0). Długość odcinka AB =wartość bezwzględna (-2 -3) =5. Długość odcinka RW =wartość bezwzględna [-3 –( -6)] =3.](https://static.zpe.gov.pl/portal/f/res-minimized/RpJx3ZLi4r5bU/1668787682/1drjpcgqRcuqNMQTFYsgap1bKk2SO9K5.svg)
Znajdziemy długości odcinków i , gdy , , , .
![Rysunek układu współrzędnych z zaznaczonymi punktami: A , B, C, D. Długość odcinka AB =wartość bezwzględna [2 –( -4)]=4. Długość odcinka CD =wartość bezwzględna (-3 –4) =7.](https://static.zpe.gov.pl/portal/f/res-minimized/RvK8AvTHsUO7i/1668787682/1ksBHGtlGPbg3bTPwLI5S2lL2slfuto6.svg)
Odcinek jest równoległy do osi . Jego długość jest równa wartości bezwzględnej różnicy pierwszych współrzędnych punktów i .
Odcinek jest równoległy do osi . Jego długość jest równa wartości bezwzględnej różnicy drugich współrzędnych punktów i .
Wielokąty w układzie współrzędnych
W niektórych wypadkach, aby obliczyć długości boków wielokąta, wygodnie jest umieścić go w układzie współrzędnych. Dla uproszczenia obliczeń staramy się, aby wierzchołki wielokąta miały współrzędne całkowite (jeśli jest to możliwe).
Umieszczenie figur w układzie współrzędnych stwarza możliwość wskazania współrzędnych ich wierzchołków oraz innych punktów charakterystycznych.
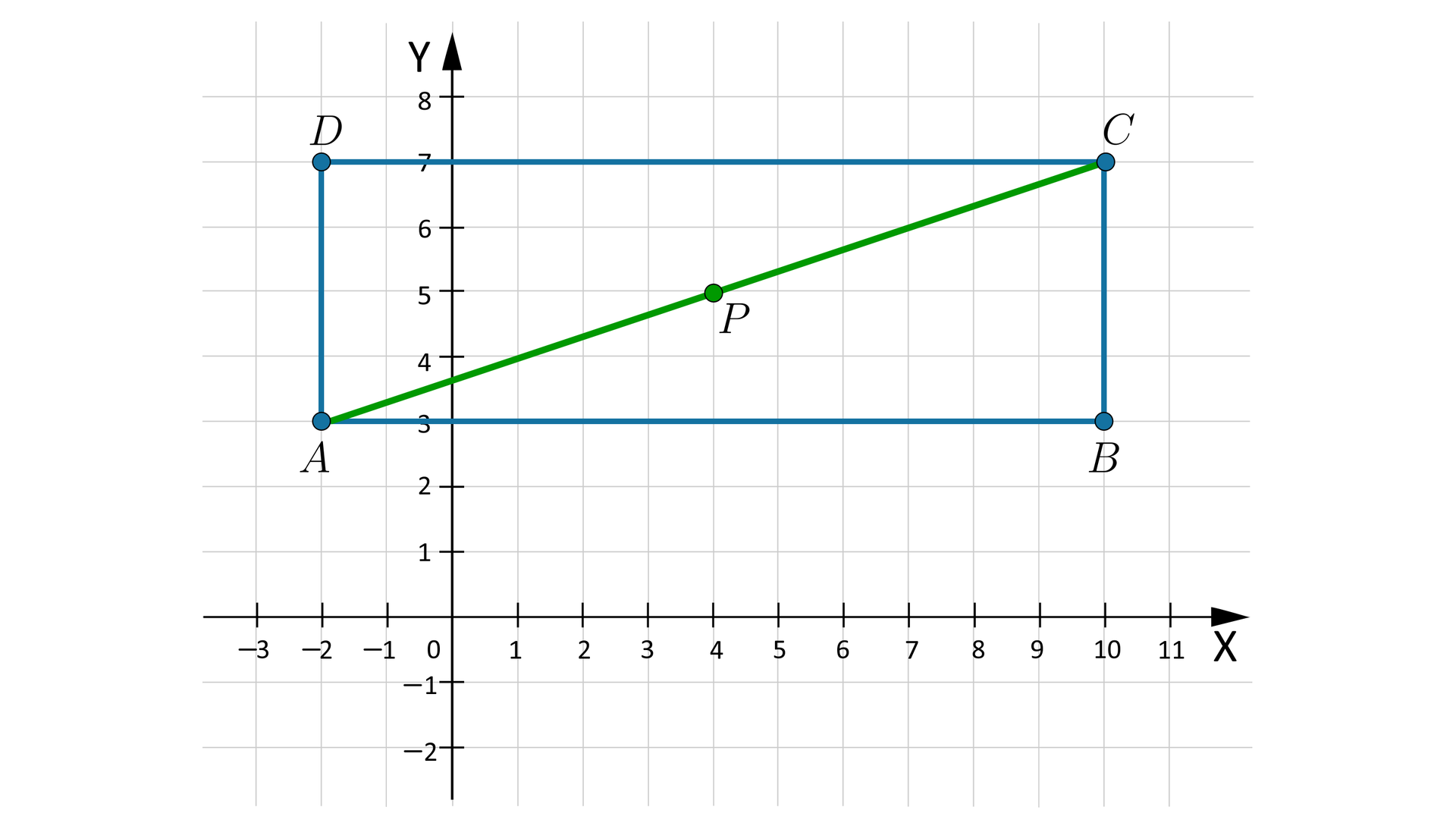
Obliczymy pole prostokąta .
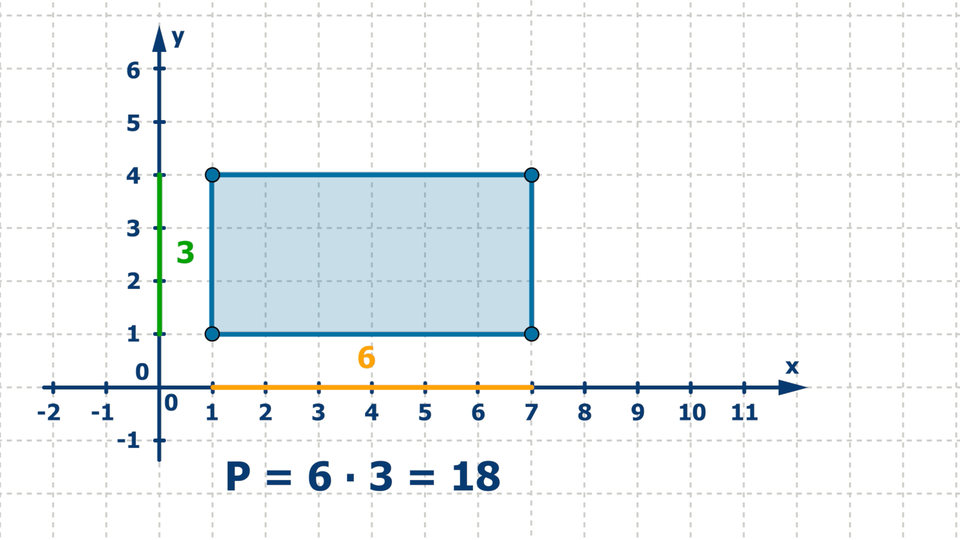
Film dostępny pod adresem /preview/resource/RM5Cpva1K9W31
Animacja przedstawia w jaki sposób możemy obliczyć pole prostokąta umieszczonego w układzie współrzędnych.
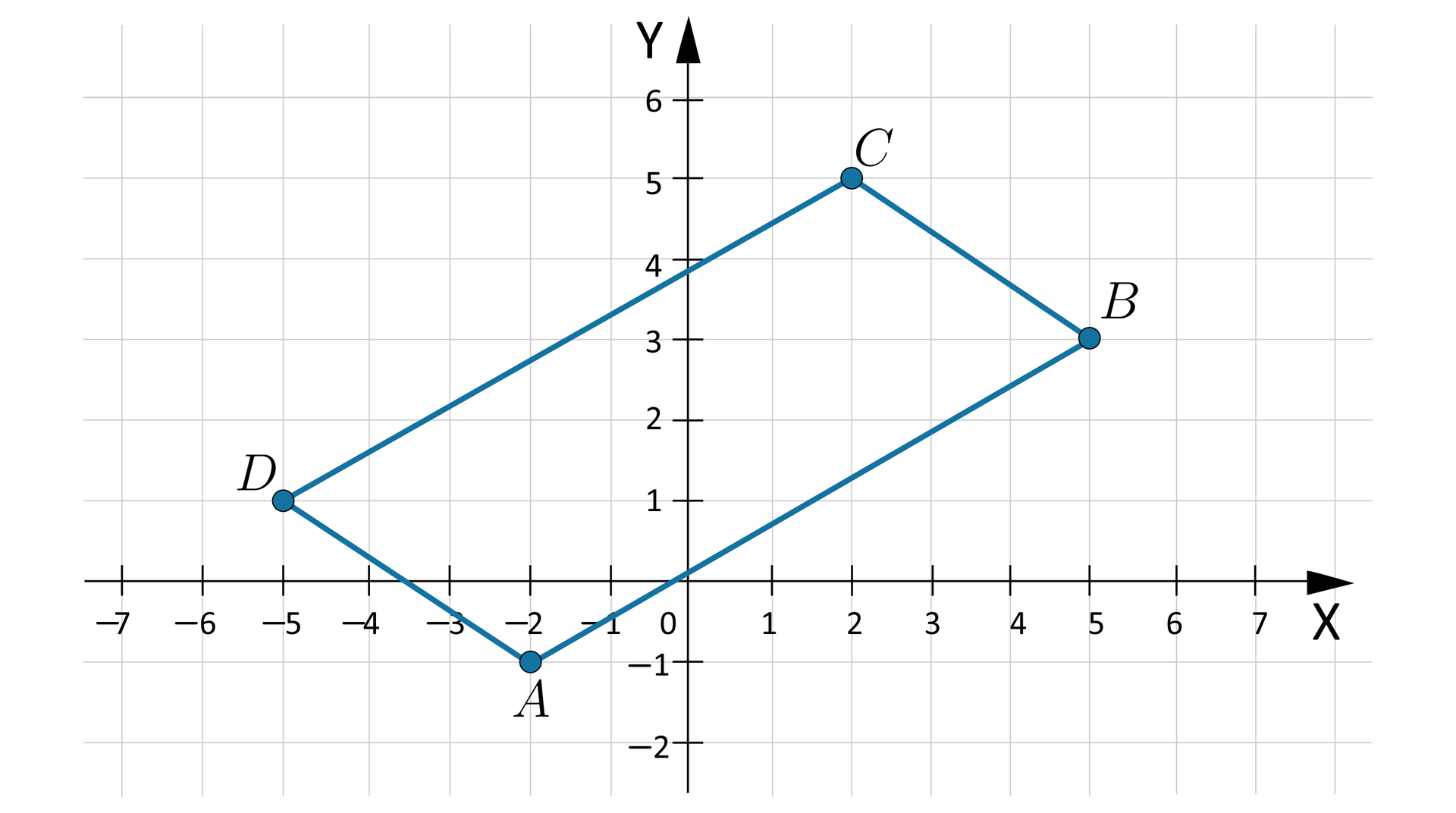
W układzie współrzędnych dane są punkty: , , . Znajdziemy taki punkt , aby wielokąt był równoległobokiem.

Oznaczmy: .
Zauważmy, że . W równoległoboku boki przeciwległe są zawsze równoległe, a ich długości są równe. Odcinek leży na prostej równoległej do prostej , a więc i do osi . Zatem .
Korzystając z tego, znajdziemy pierwszą współrzędną punktu .
Z rysunku widać, że liczba jest dodatnia, zatem większa od . Ponieważ
, więc lub . Stąd
lub .
Ponieważ , więc .
Liczba jest równa drugiej współrzędnej punktu (bo odcinek jest równoległy do osi ), więc
.
Odpowiedź: Szukanym punktem jest punkt .

Zaznacz w układzie współrzędnych punkt o podanych współrzędnych.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Podaj współrzędne punktu .
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Punkty , i są trzema wierzchołkami równoległoboku. Umieść punkt tak, aby zbudować równoległobok .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Dany jest trójkąt . Umieść odcinek tak, aby był wysokością tego trójkąta poprowadzoną z wierzchołka .
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Dany jest trójkąt . Umieść dane odcinki tak, aby były środkowymi tego trójkąta.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
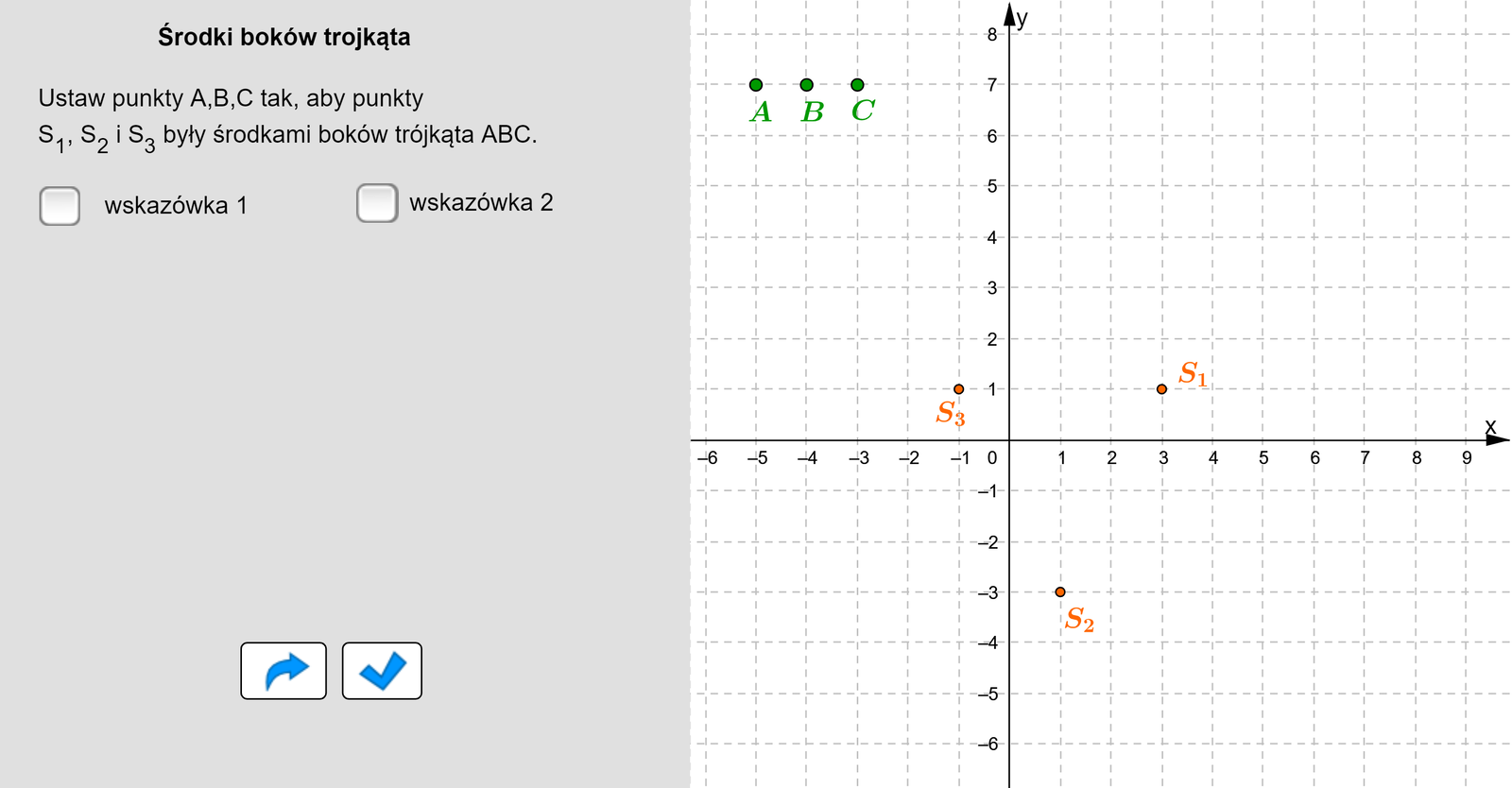
Umieść punkty , i tak, aby punkty , i były środkami boków utworzonego trójkąta .
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
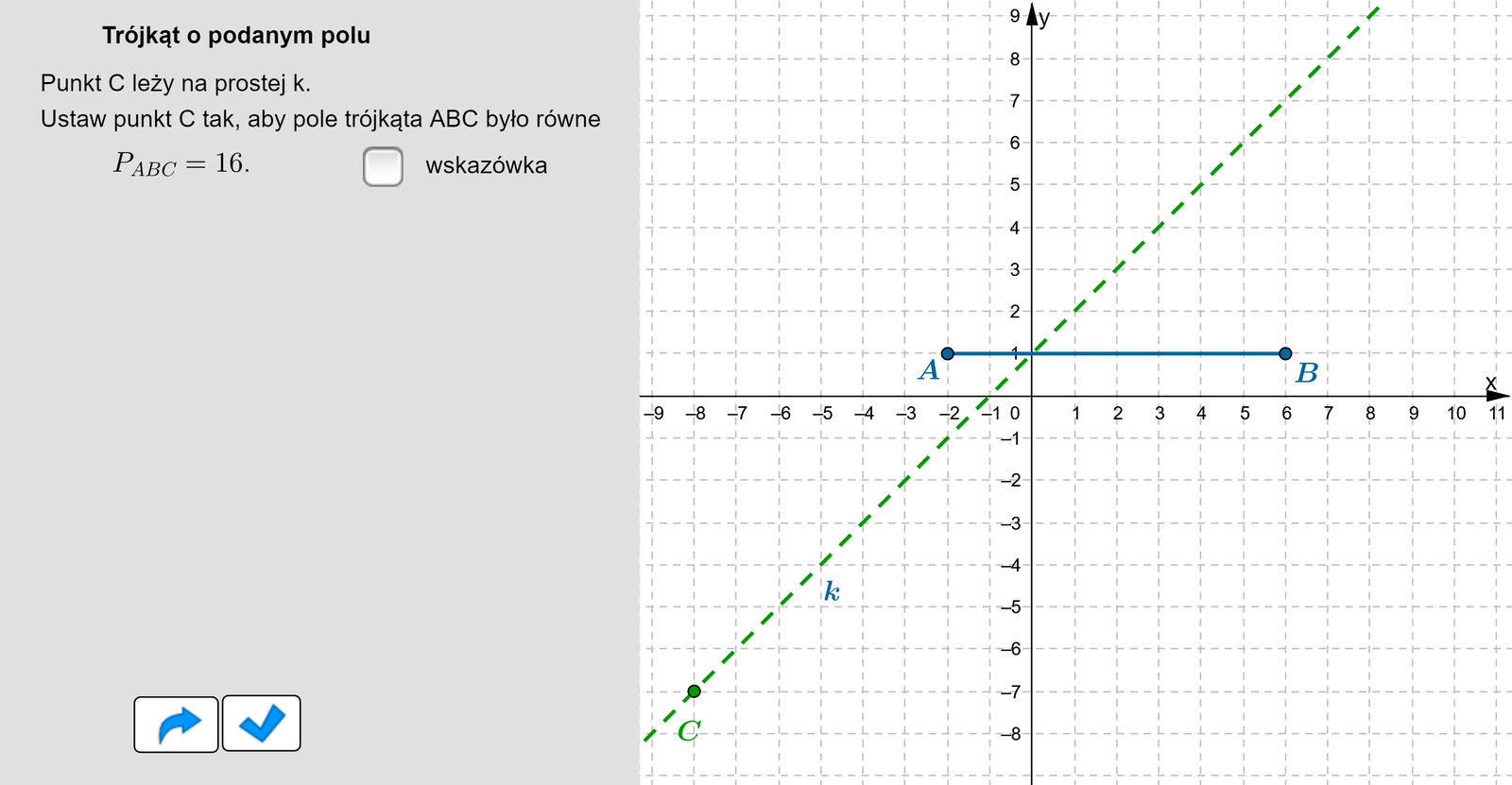
Umieść punkt tak, aby pole trójkąta było równe tyle, ile wskazano w aplecie.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
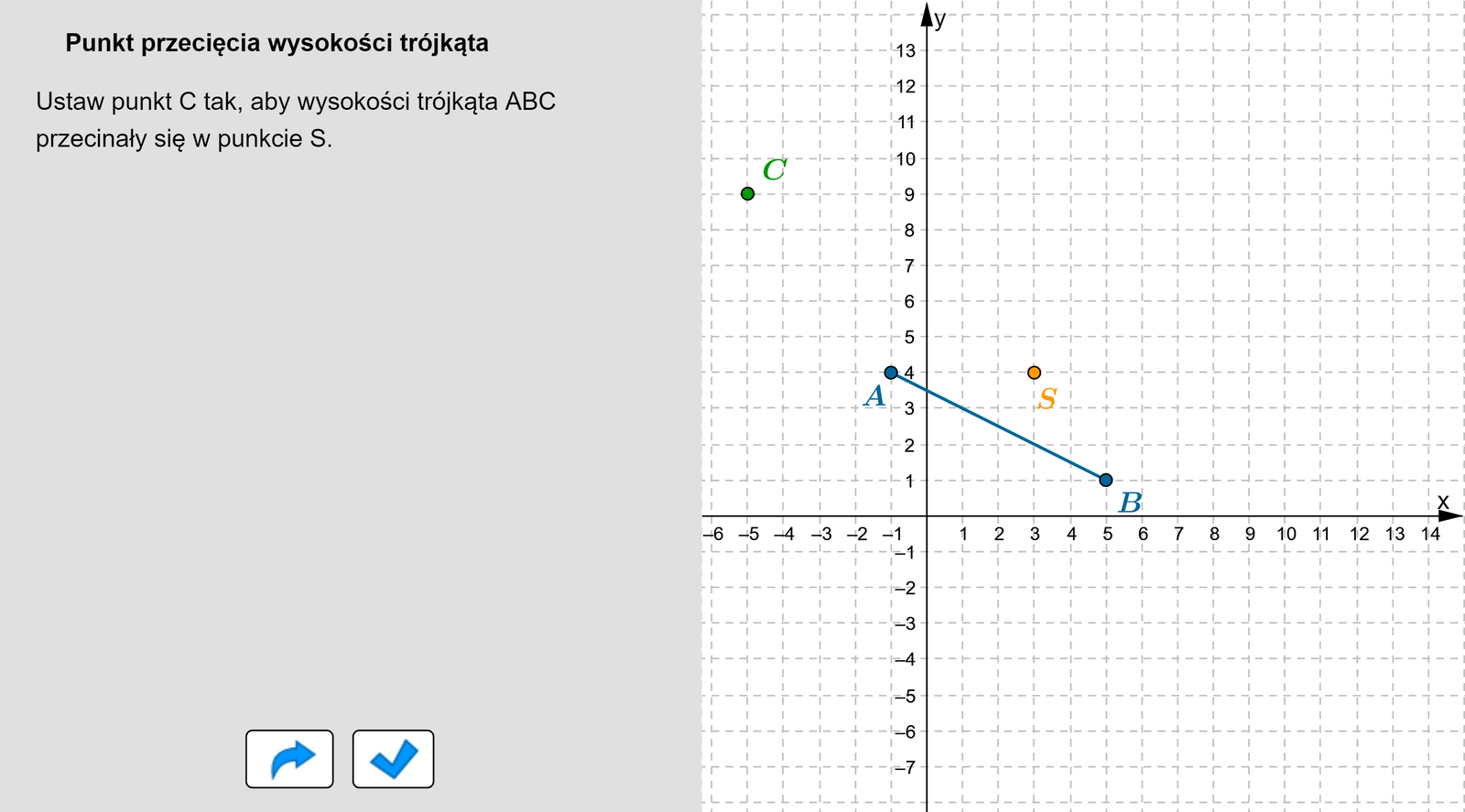
Odcinek jest bokiem, a jest punktem przecięcia wysokości (ortocentrum) trójkąta . Wyznacz wierzchołek trójkąta .
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
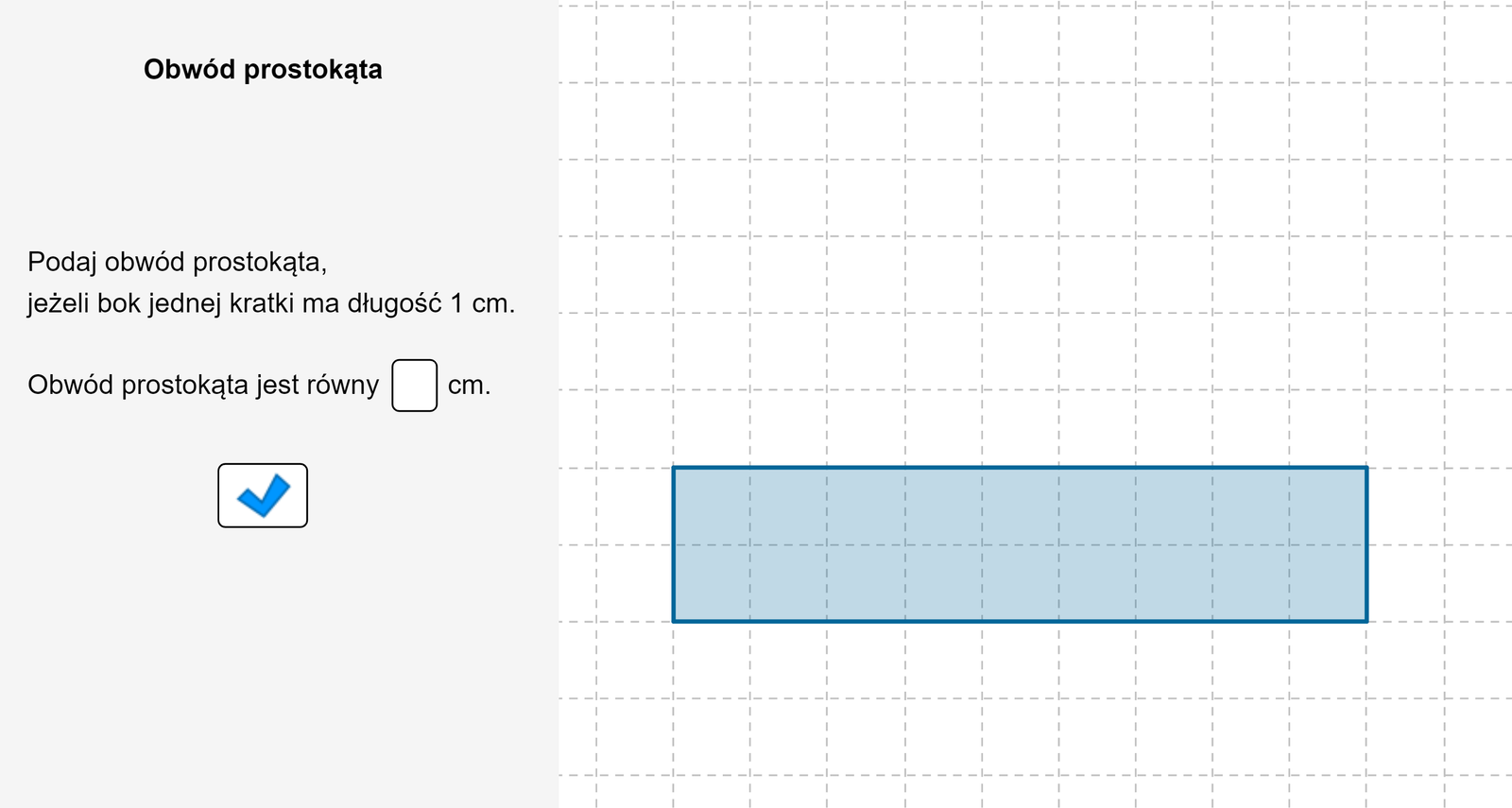
Zapoznaj się z apletem i postępuj zgodnie z poleceniami.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Zapoznaj się z apletem i postępuj zgodnie z poleceniami.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Zapoznaj się z apletem i postępuj zgodnie z poleceniami.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Zapoznaj się z apletem i postępuj zgodnie z poleceniami.
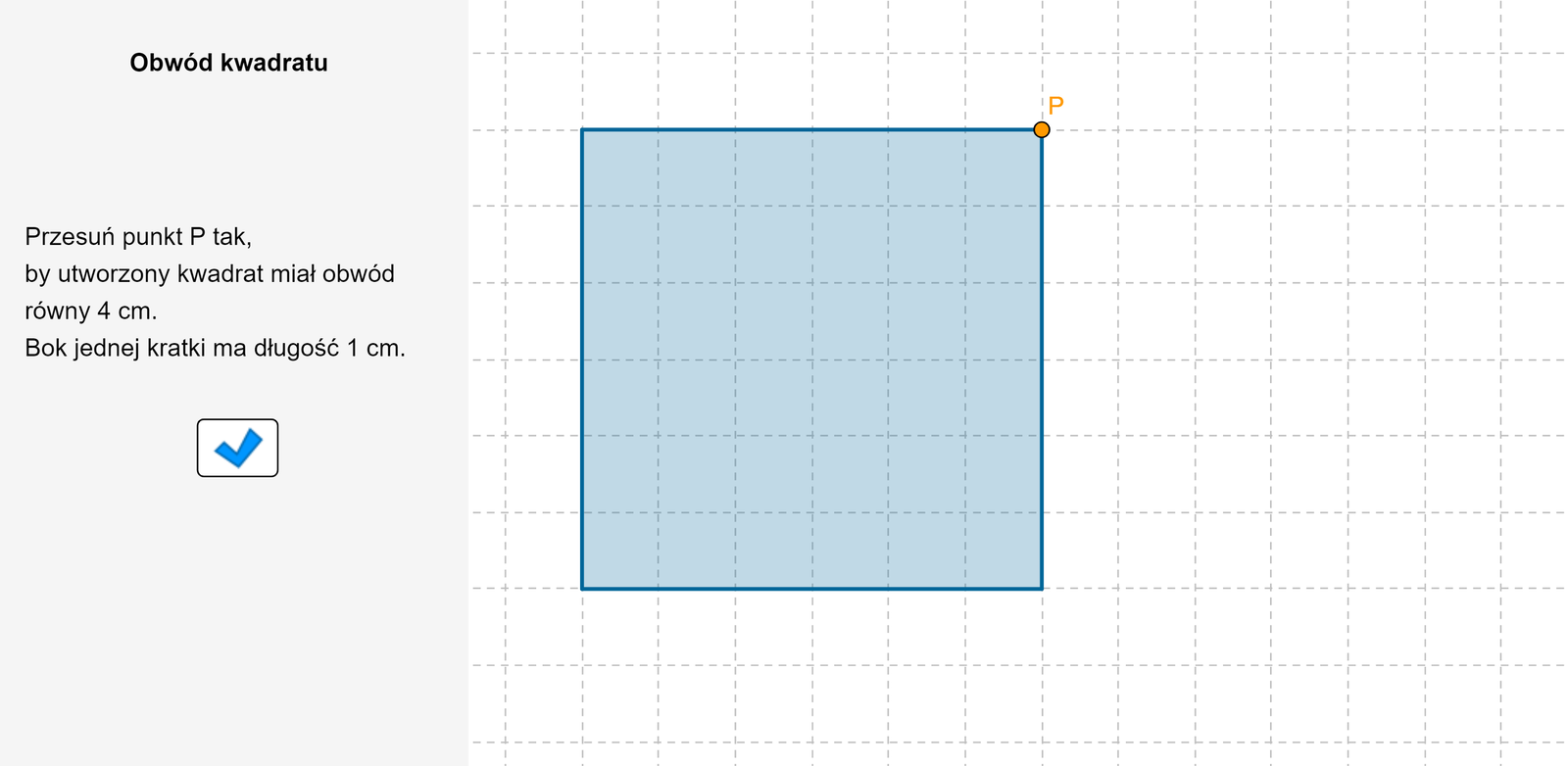
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Zapoznaj się z apletem i postępuj zgodnie z poleceniami.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Zapoznaj się z apletem i postępuj zgodnie z poleceniami.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Zapoznaj się z apletem i postępuj zgodnie z poleceniami.
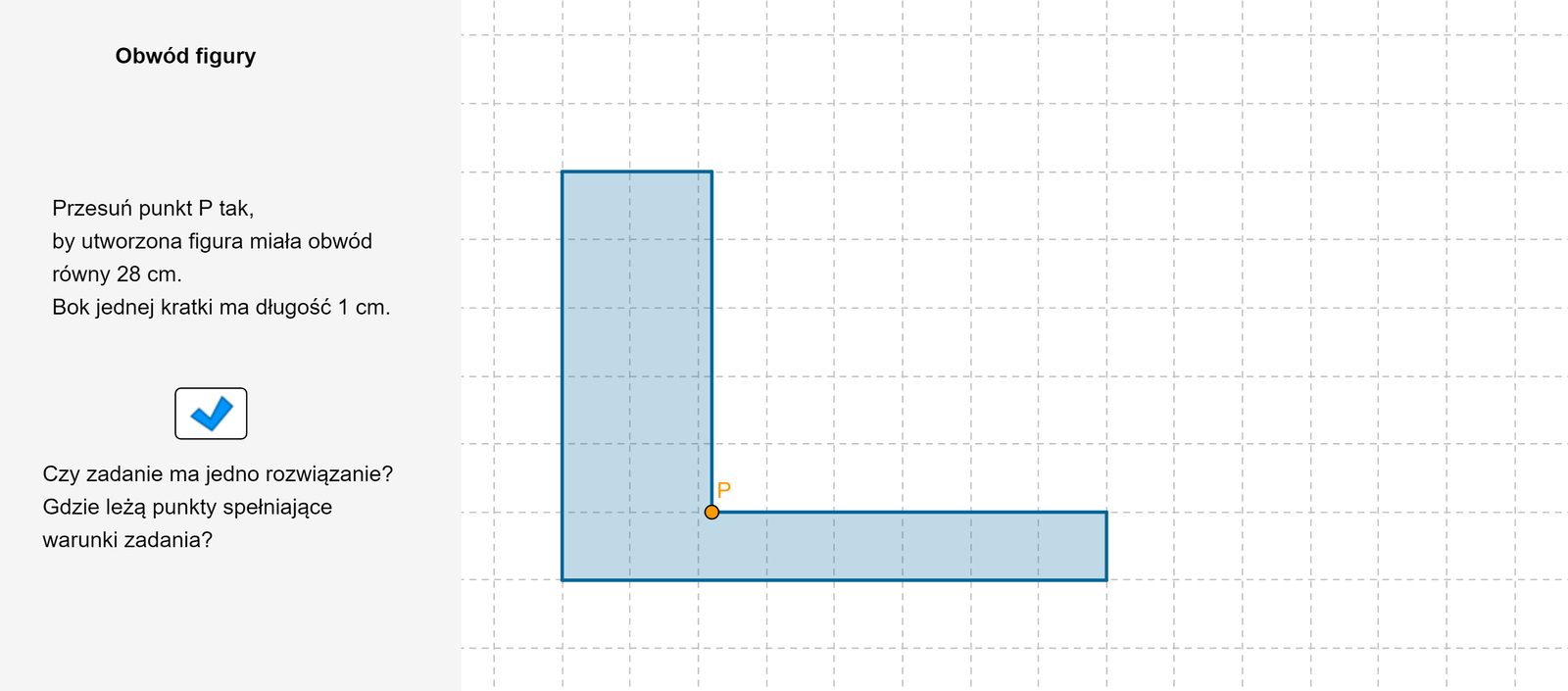
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Zapoznaj się z apletem i postępuj zgodnie z poleceniami.
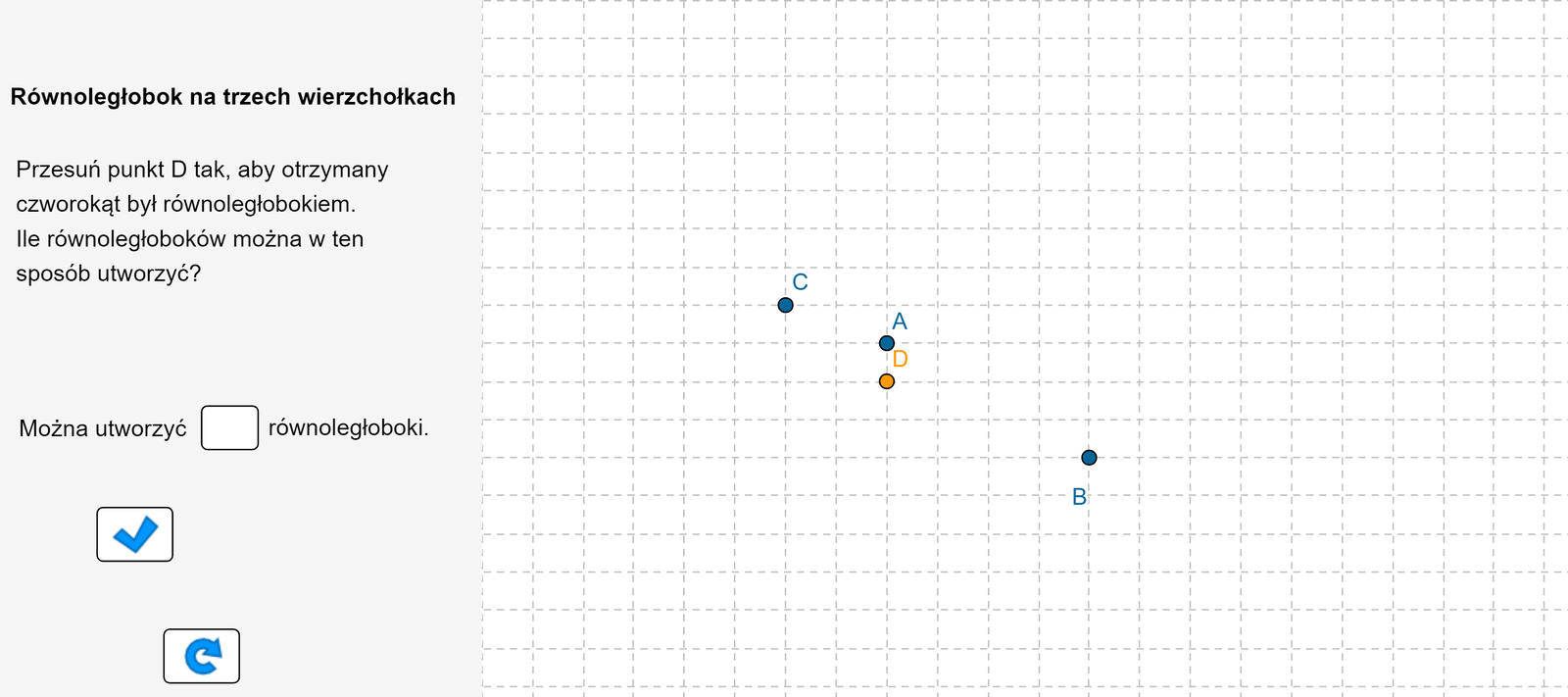
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Jeśli na obu osiach układu współrzędnych jest ta sama jednostka, to za jednostkę pola przyjmujemy kwadrat o boku, którego długość jest równa jednostce każdej osi.
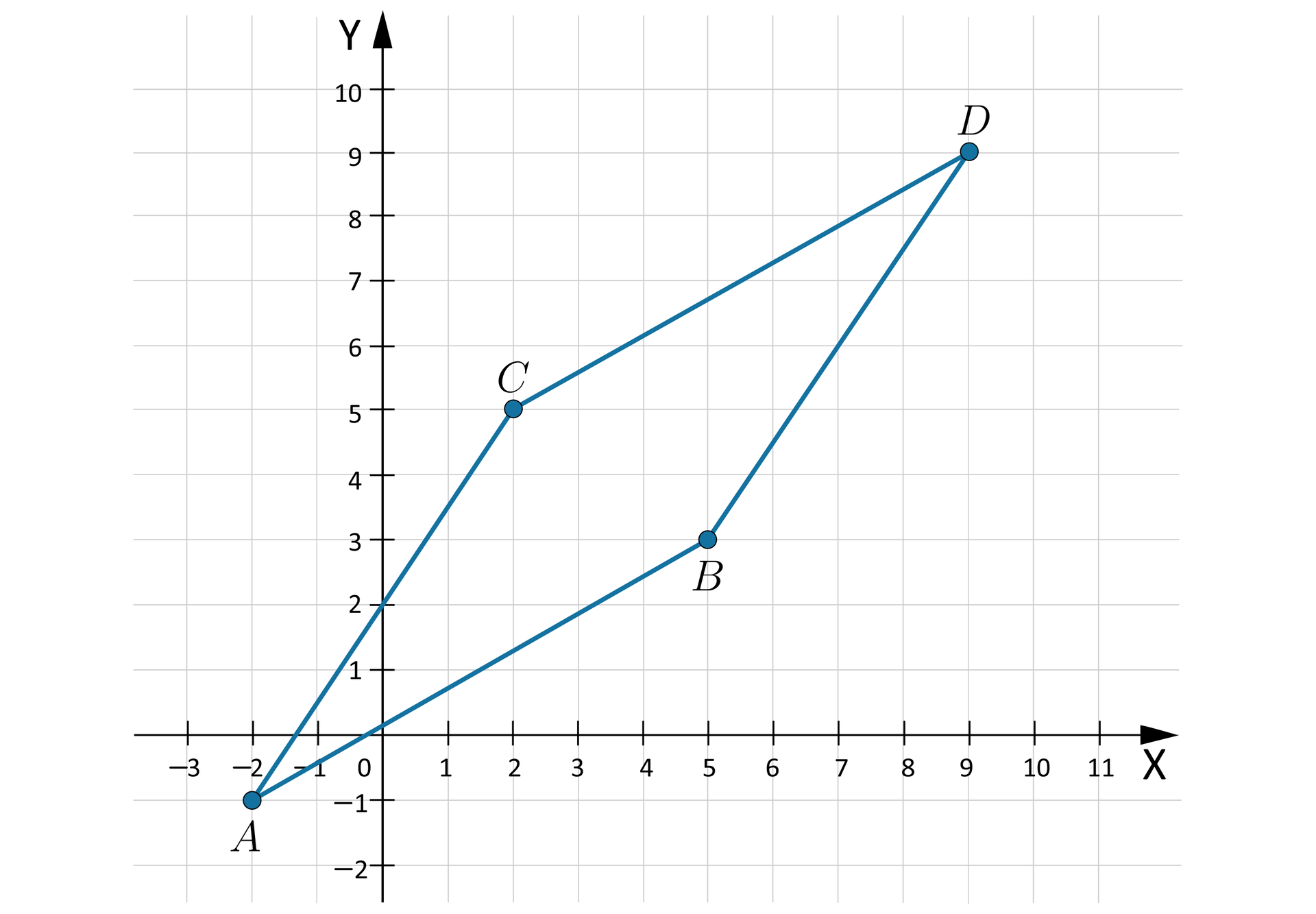
Obliczymy pole trapezu , gdzie , , , .

sposób
Zauważmy, że trapez jest równoramienny, więc jego pole jest równe polu prostokąta , długości i szerokości . Zatem pole tego prostokąta, a więc i pole trapezu, jest równe .

sposób
Obliczamy długości , podstaw oraz wysokość trapezu i korzystamy ze wzoru

Odpowiedź: Pole trapezu jest równe .
, , . Połącz kolejno te punkty. Figura, którą otrzymasz to Możliwe odpowiedzi: 1. trójkąt prostokątny, 2. trójkąt rozwartokątny, 3. trójkąt ostrokątny, 4. trójkąt równoramienny
- trójkąt prostokątny
- trójkąt rozwartokątny
- trójkąt ostrokątny
- trójkąt równoramienny
, , . Zaznacz, jakie współrzędne ma wierzchołek . Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Zaznacz w układzie współrzędnych podane punkty: , , oraz taki punkt , aby otrzymany czworokąt był
równoległobokiem, który nie jest prostokątem?
prostokątem, który nie jest kwadratem?
kwadratem?
rombem, który nie jest kwadratem?
Uzasadnij swój wybór. Czy w każdym przypadku udało Ci się znaleźć rozwiązanie?
W układzie współrzędnych zaznaczono trzy punkty, które są wierzchołkami pewnego wielokąta: , , . Jakie współrzędne powinien mieć wierzchołek , aby otrzymany czworokąt był:
równoległobokiem, który nie jest prostokątem?
prostokątem, który nie jest kwadratem?
kwadratem?
rombem, który nie jest kwadratem?
Uzasadnij swój wybór. Czy w każdym przypadku udało Ci się znaleźć rozwiązanie?
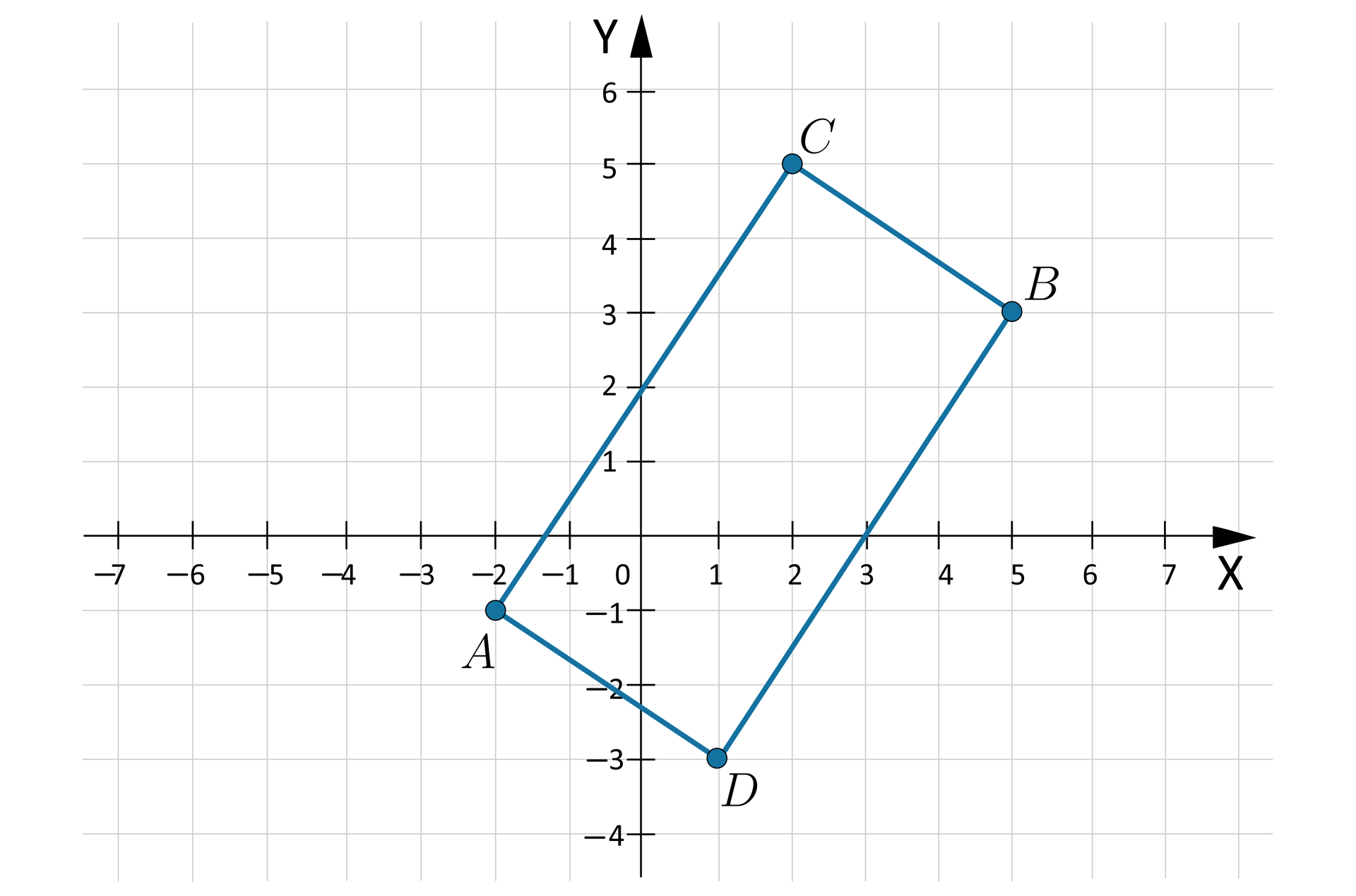
W układzie współrzędnych umieszczono równoległobok, tak jak na rysunku.

- Punkt o współrzędnych należy do równoległoboku .
- Punkt o współrzędnych jest wierzchołkiem równoległoboku .
- Pierwsze współrzędne wierzchołków i są równe.
Narysuj w układzie współrzędnych prostokąt, którego przekątne przecinają się w punkcie i jeden z jego wierzchołków ma współrzędne , a drugi z jego wierzchołków ma współrzędnie . Odczytaj współrzędne wierzchołków tego prostokąta.
W układzie współrzędnych zaznaczono prostokąt , którego przekątne przecinają się w punkcie i wierzchołek ma współrzędne , a wierzchołek ma współrzędne . Podaj współrzędne wierzchołków tego prostokąta.
Zapoznaj się z apletem i postępuj zgodnie z poleceniami.
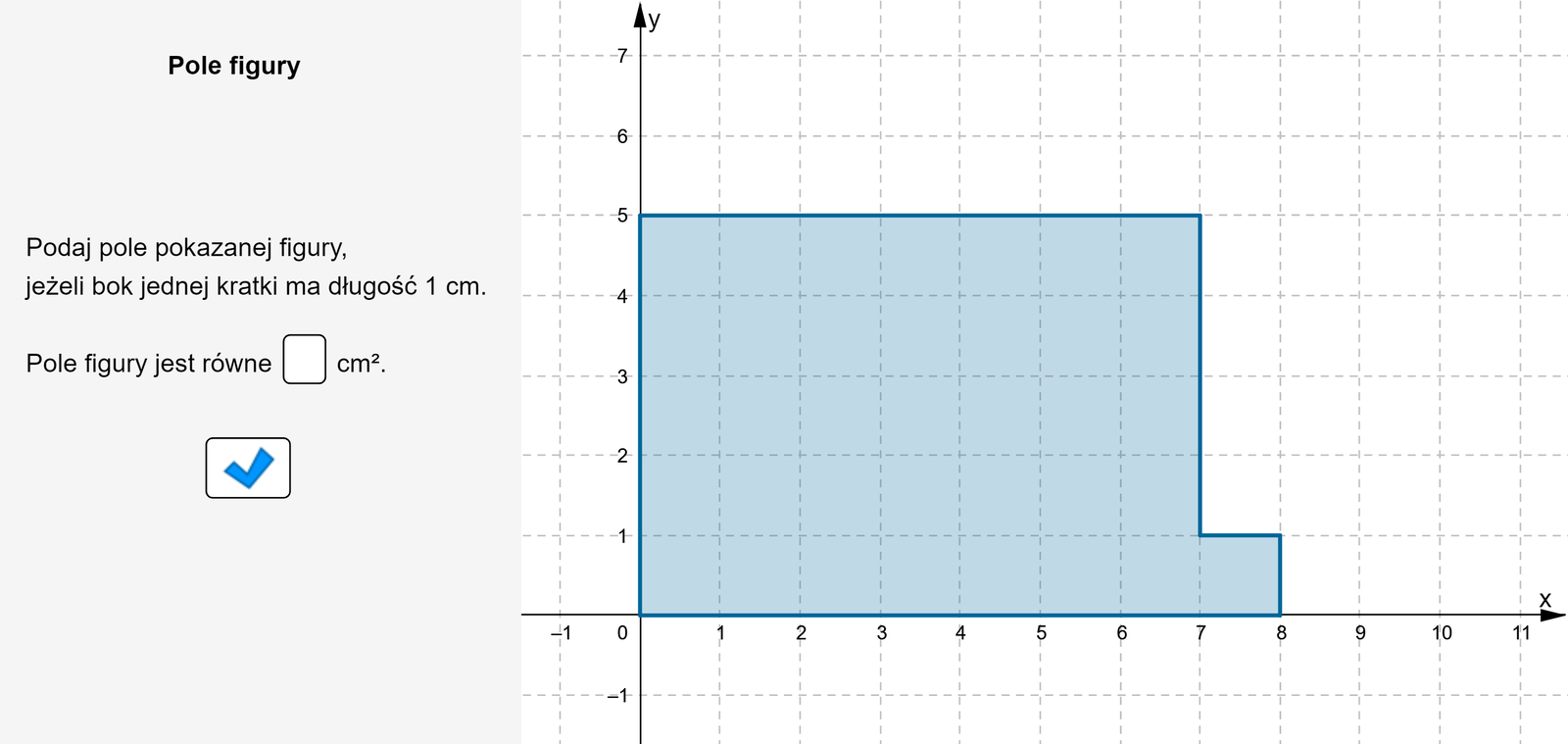
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Zapoznaj się z apletem i postępuj zgodnie z poleceniami.
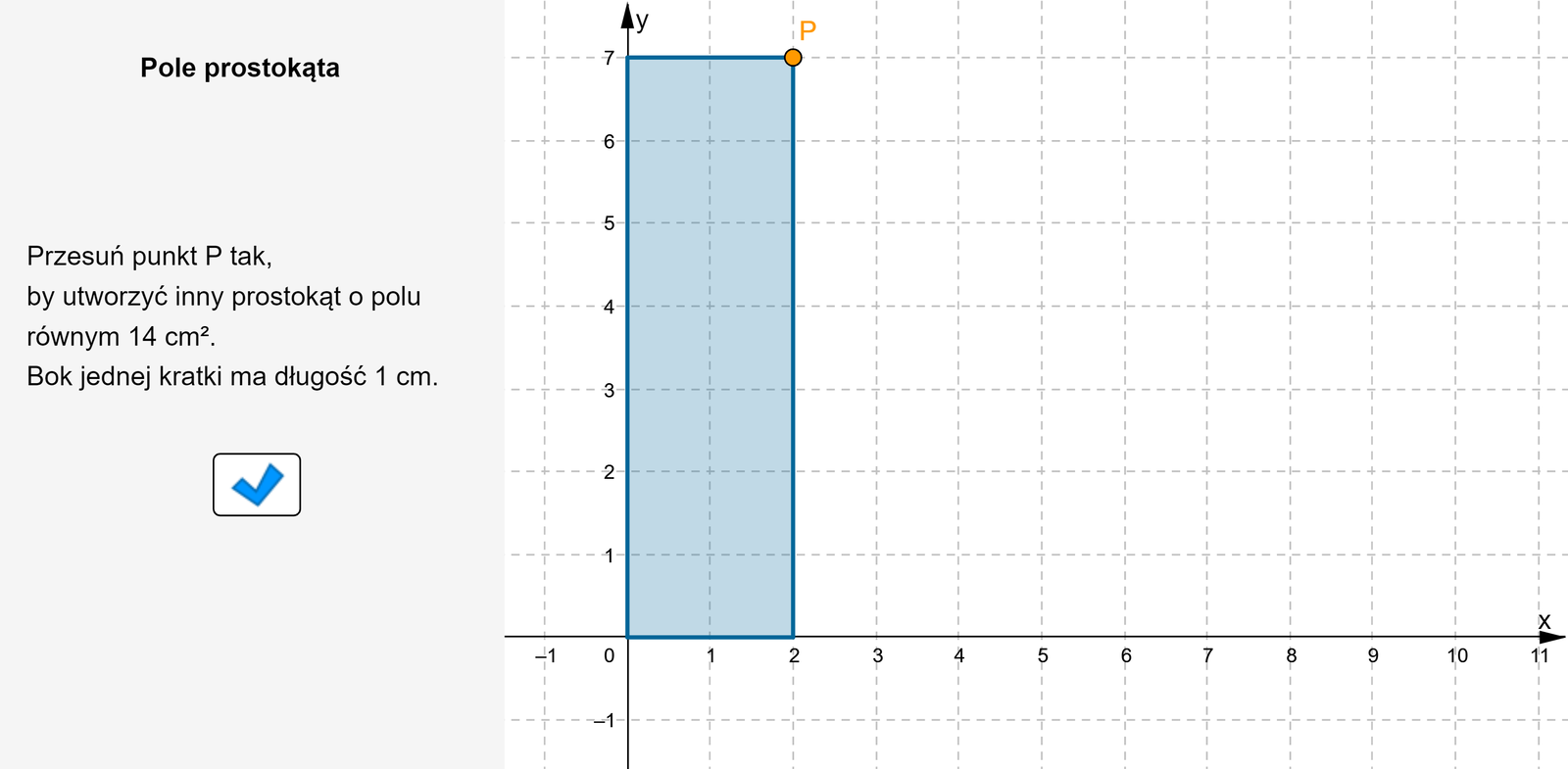
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Zapoznaj się z apletem i postępuj zgodnie z poleceniami.
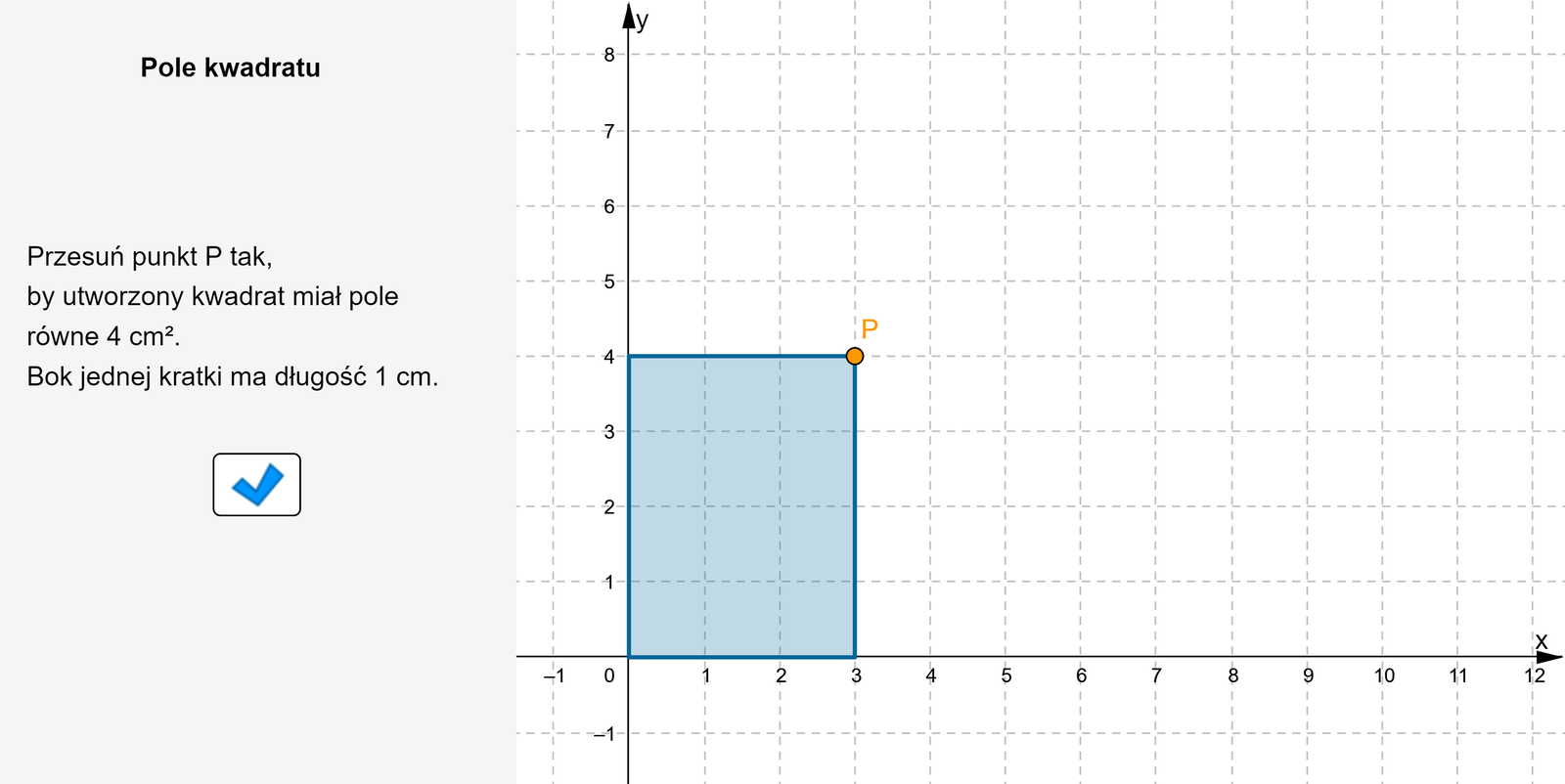
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Zapoznaj się z apletem i postępuj zgodnie z poleceniami.
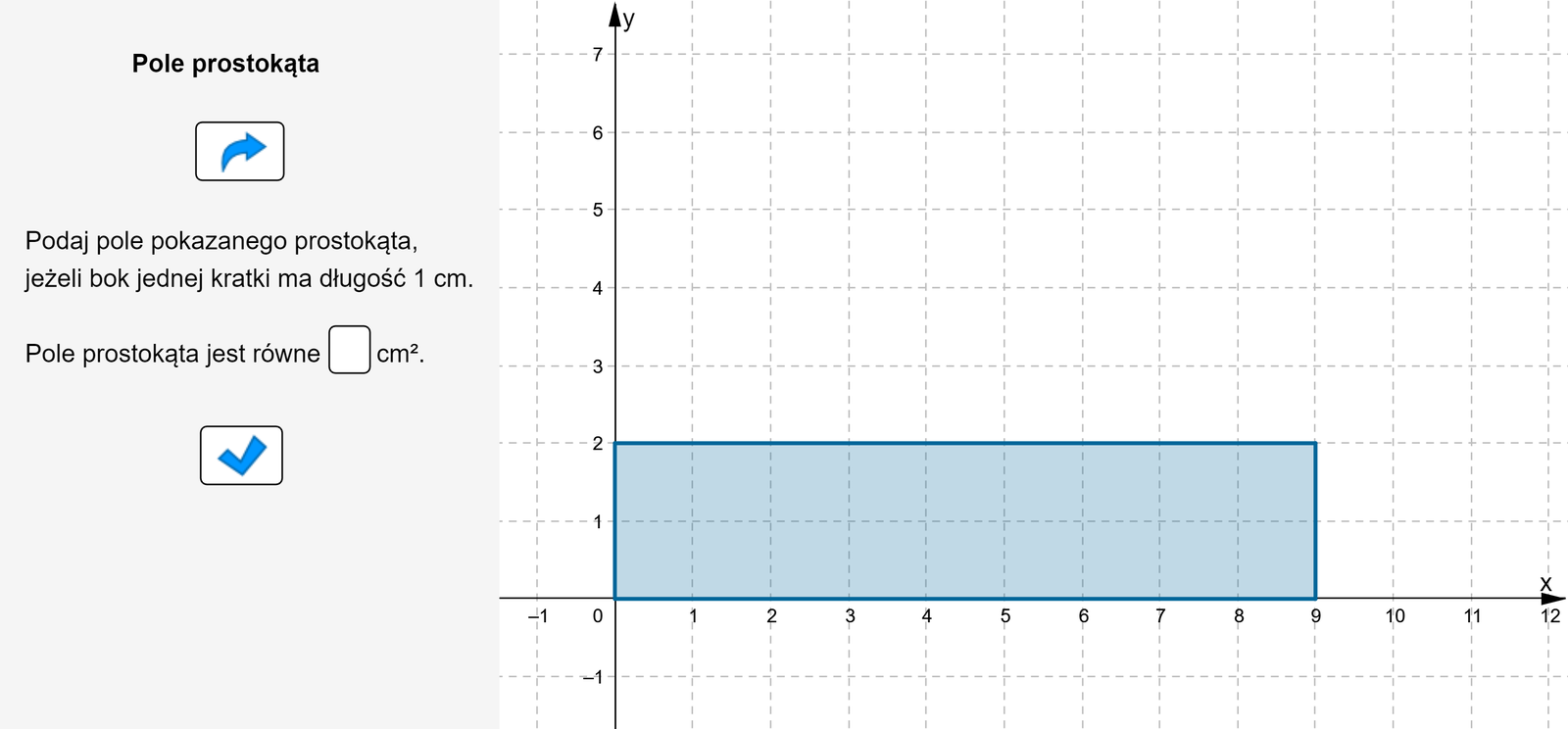
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Zapoznaj się z apletem i postępuj zgodnie z poleceniami.
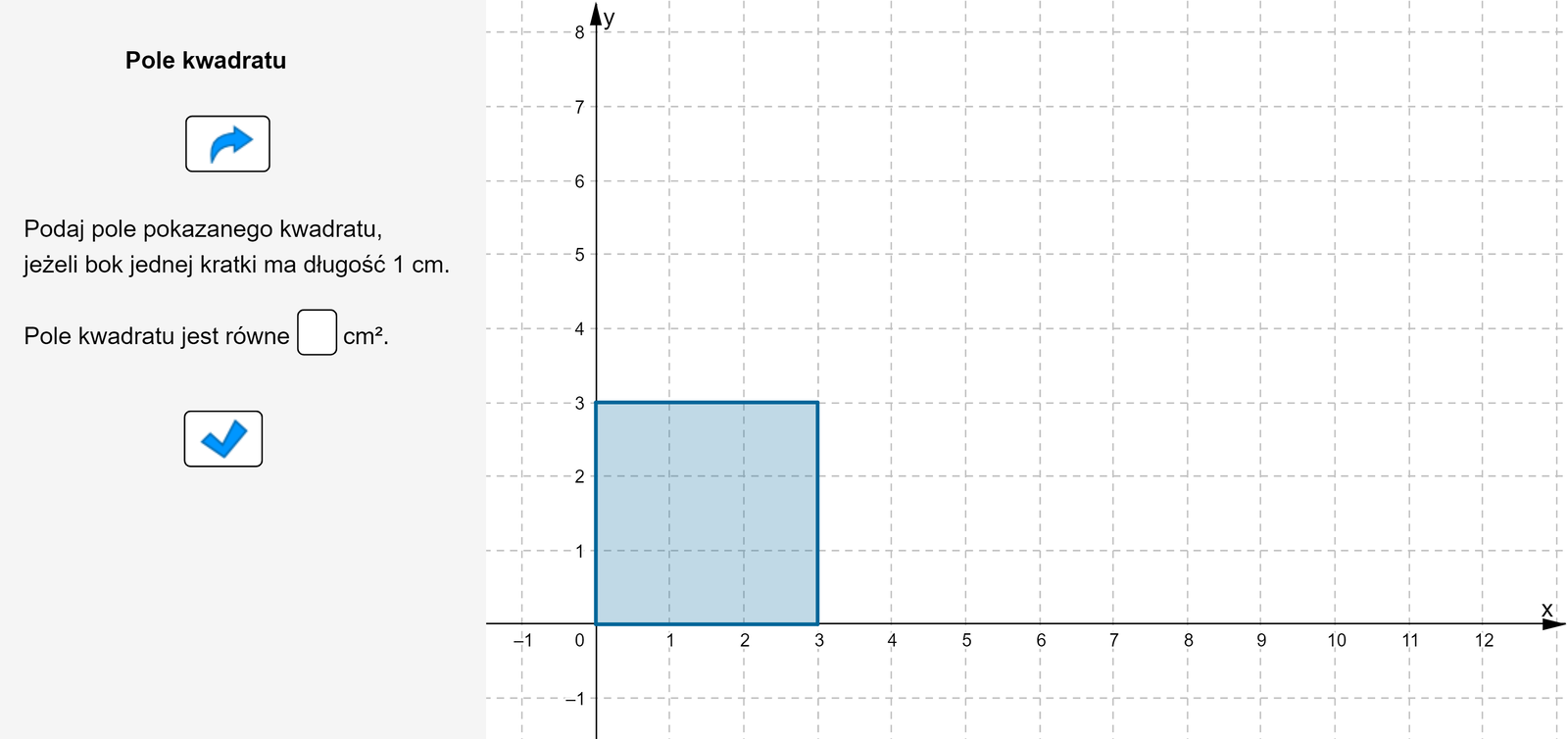
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DaF3gtRC9
Punkty , , , są kolejnymi wierzchołkami kwadratu o polu równym 1. , 2. , 3. , 4. , 5. , 6. .
Punkty , , , są kolejnymi wierzchołkami kwadratu o polu równym 1. , 2. , 3. , 4. , 5. , 6. .
Dla trójkąta różnobocznego podano tylko przykładowe współrzędne wierzchołka . Istnieje nieskończenie wiele takich punktów – każdy punkt, którego rzędna jest równa lub (poza wyjątkami, gdy jest to trójkąt równoramienny).
Zaznacz w układzie współrzędnych punkty: , , , , . Oblicz pole
czworokąta ,
czworokąta .
W układzie współrzędnych zaznaczono punkty: , , , , . Oblicz pole
czworokąta ,
czworokąta .
Układ współrzędnych
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.