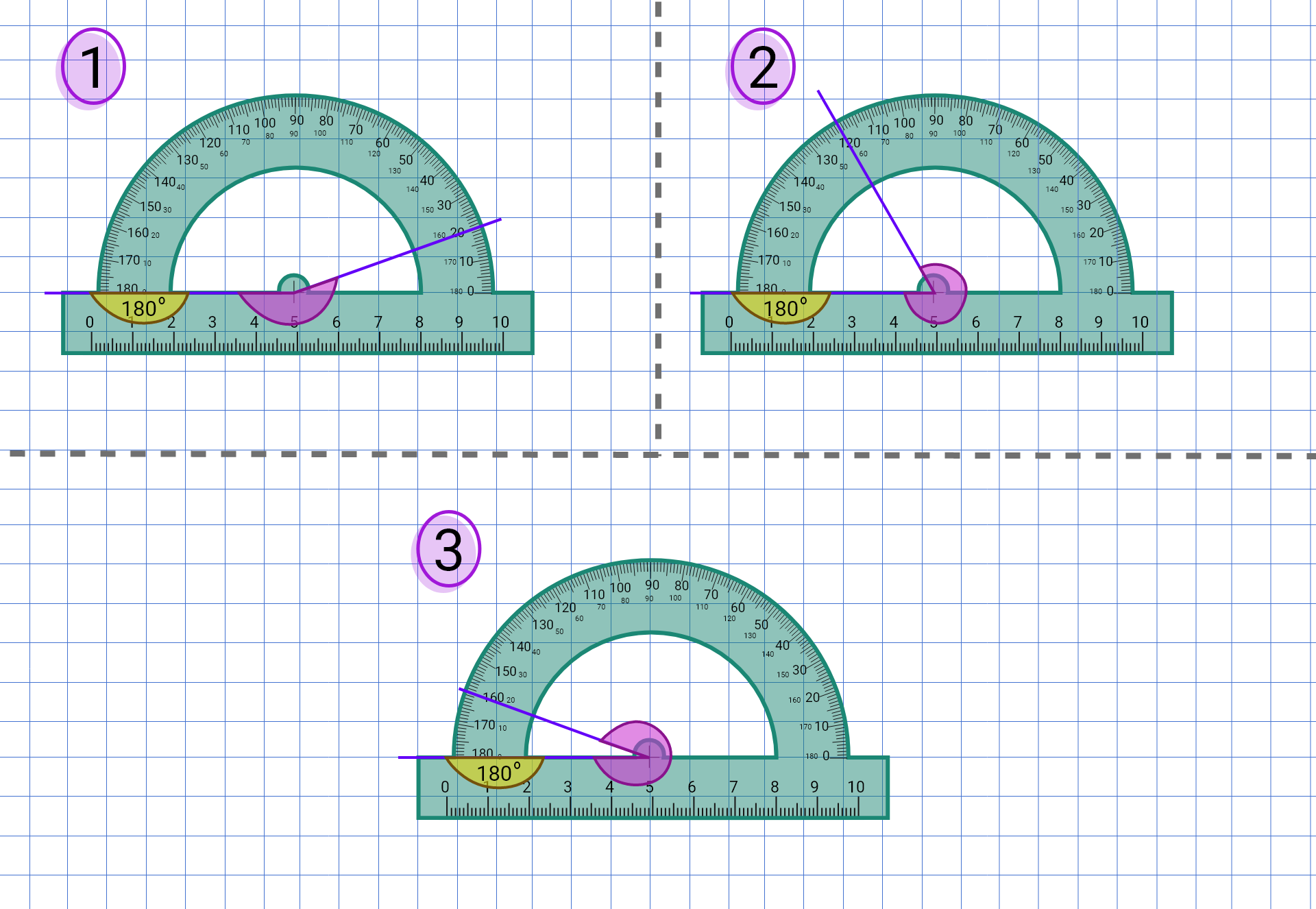
5. Mierzenie kątów
Linijka służy do rysowania odcinków, prostych, półprostych oraz do mierzenia długości odcinków. Podobne funkcje ma ekierka, ale dodatkowo można ją wykorzystać na przykład do sprawdzania prostopadłości prostych. Jest również przyrząd do mierzenia kątów i rysowania kątów o danej mierze. Jest to kątomierz.
Film dostępny pod adresem /preview/resource/ROF0Pcg785YvY
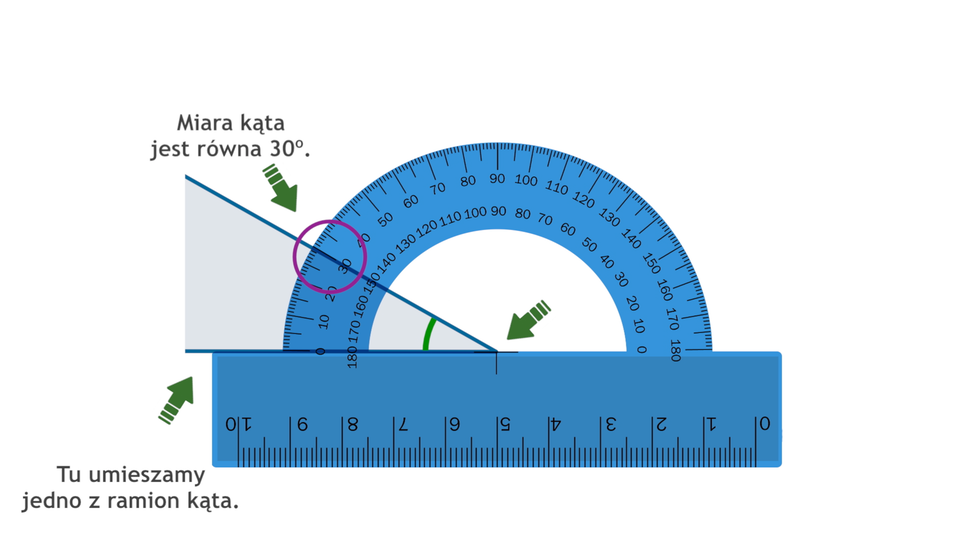
Animacja pokazuje, w jaki sposób mierzyć kąty za pomocą kątomierza.
Na tarczy zegarowej wskazówki tworzą różne kąty. Jak położone są wskazówki o godzinie ?
Film dostępny pod adresem /preview/resource/R12TXT2a5W3AC
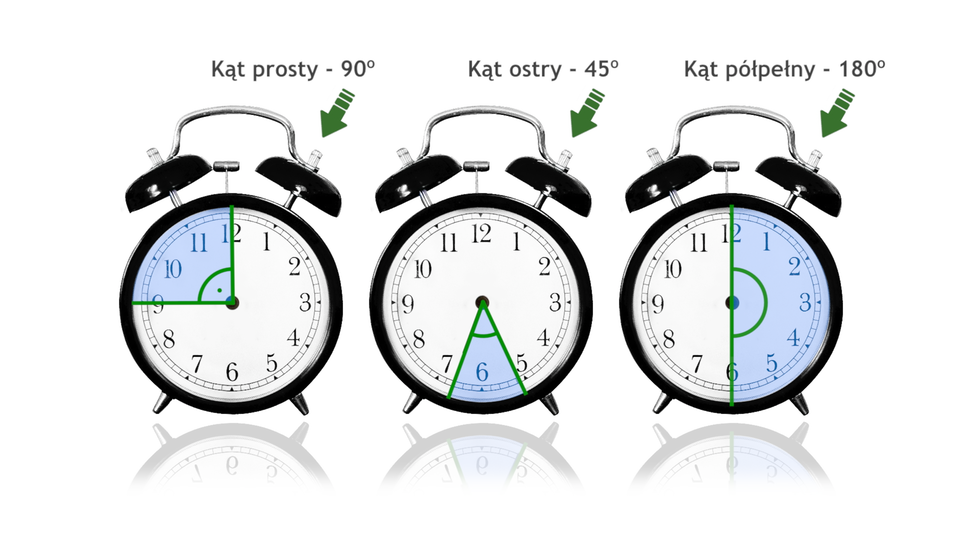
Animacja przedstawia różne rodzaje kątów na podstawie wskazówek zegara.
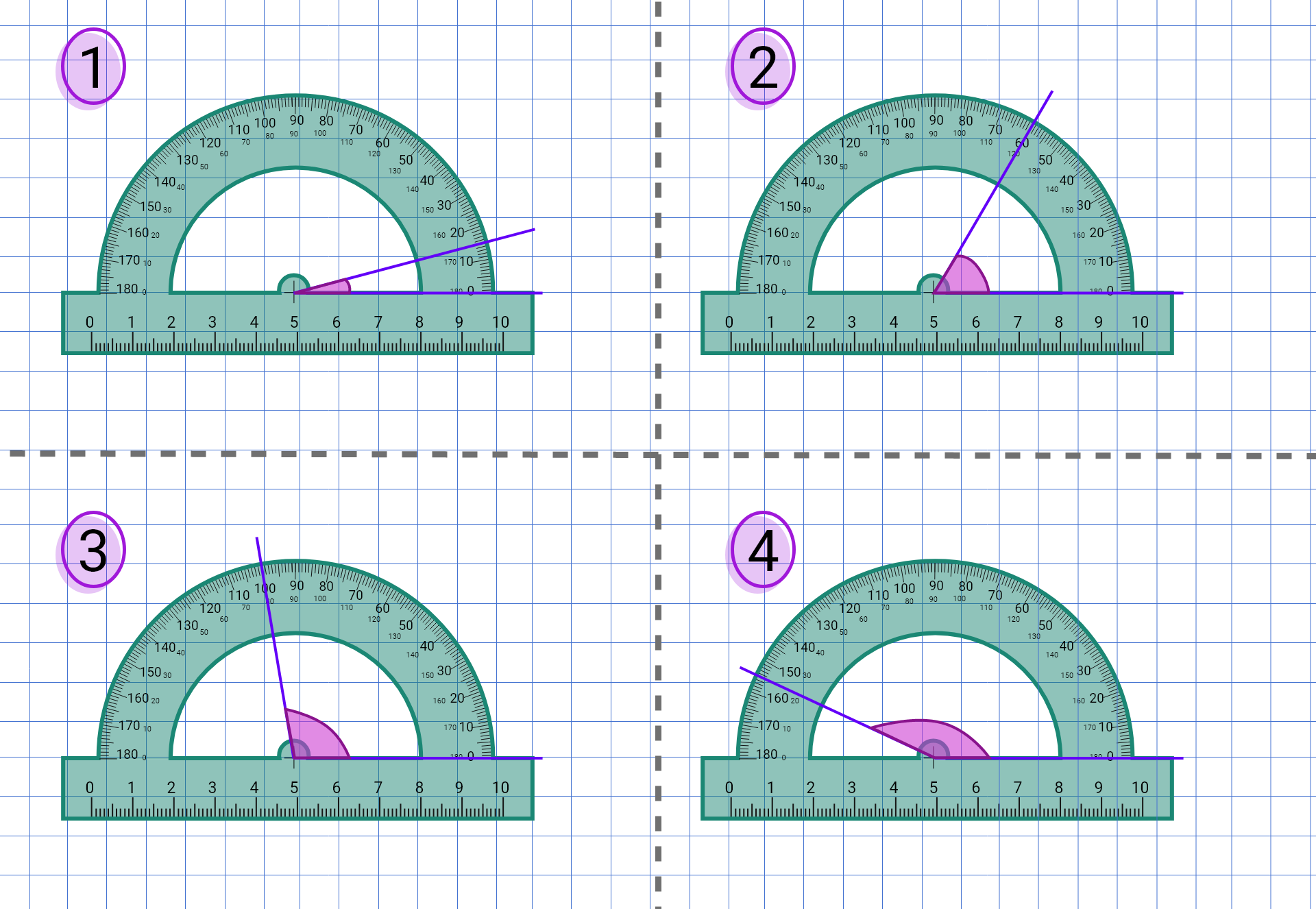
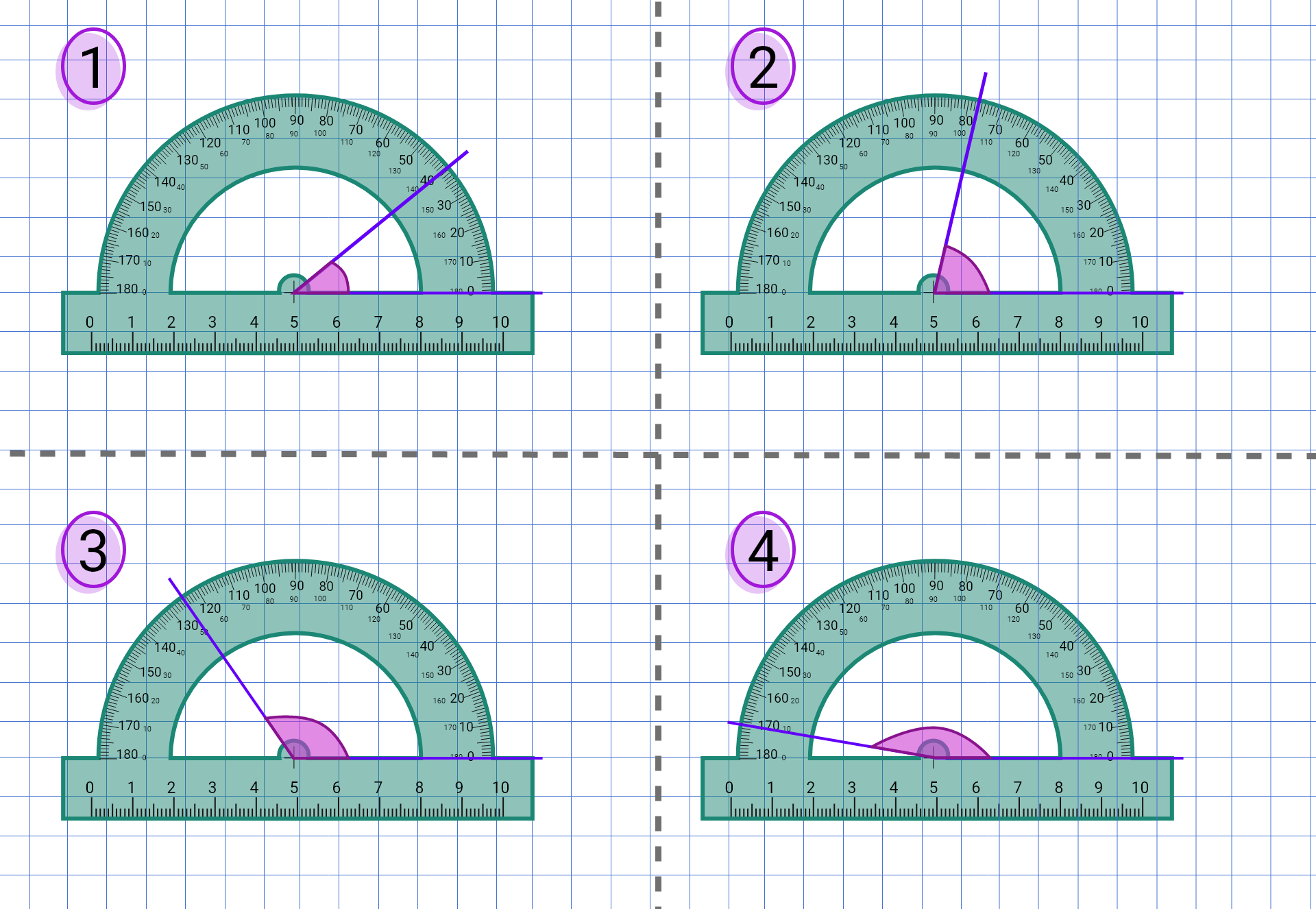
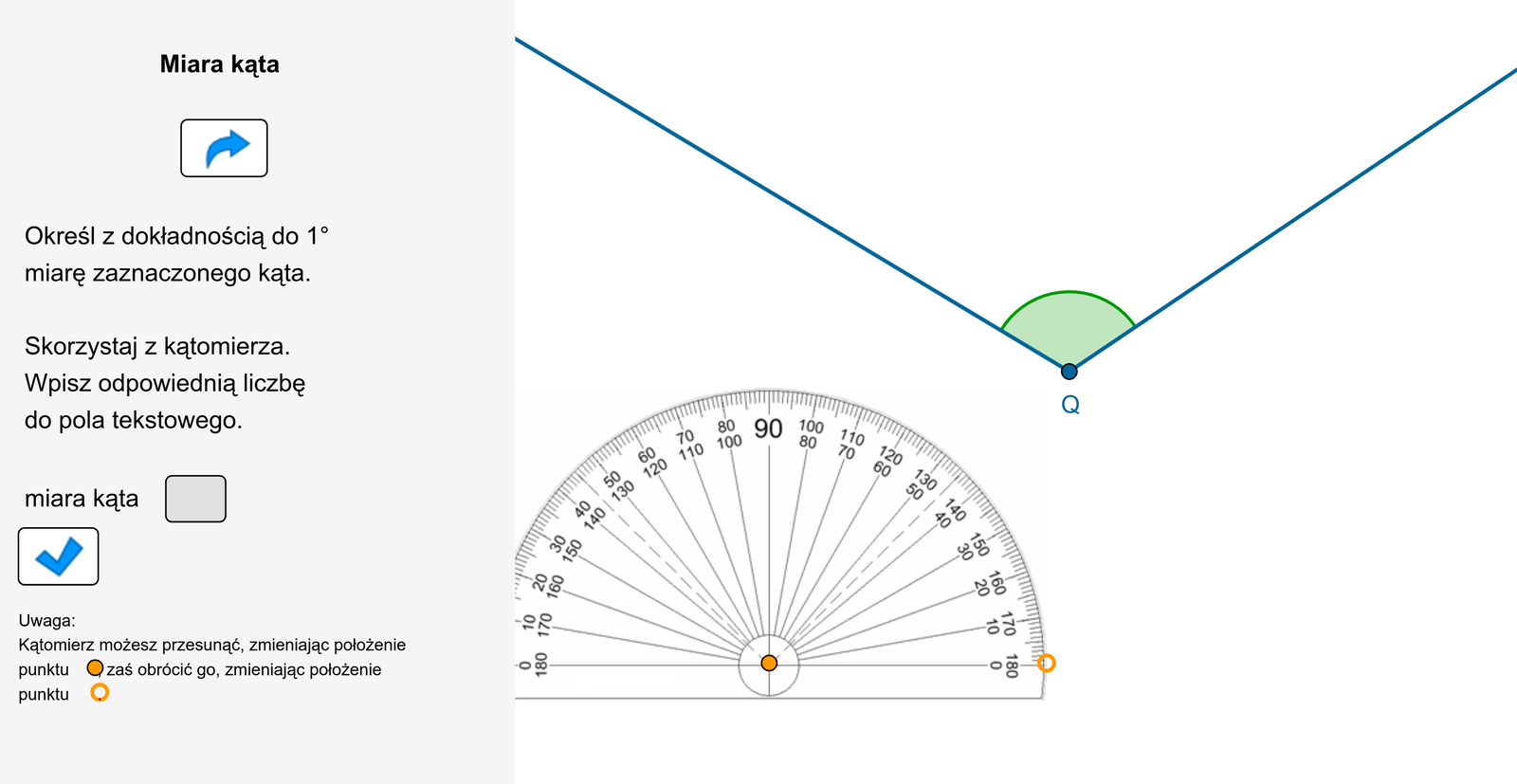
Zapoznaj się z poniższym apletem dotyczącym mierzenia kątów za pomocą kątomierza i wykonaj polecenia w nim zawarte.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DUz18dm0u
Przesuwając punkt , ustaw tak ramię kąta , aby miara tego kąta była równa podanej wartości. Skorzystaj z kątomierza.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DUz18dm0u
Jeśli potrafisz mierzyć kąty, potrafsz je także rysować. Zapoznaj się z poniższą animacją.
Film dostępny pod adresem /preview/resource/RjXVpUQIbXIq2
Animacja pokazuje, w jaki sposób narysować kąt o mierze za pomocą kątomierza.
Gdy chcemy zaznaczyć kąt na rysunku, nie musimy wypełniać wnętrza kąta kolorem. Można zaznaczyć kąt łukiem.

Aby oznaczyć kąt, można najpierw oznaczyć trzy punkty: wierzchołek kąta i dwa dowolne punkty leżące na obu jego ramionach.
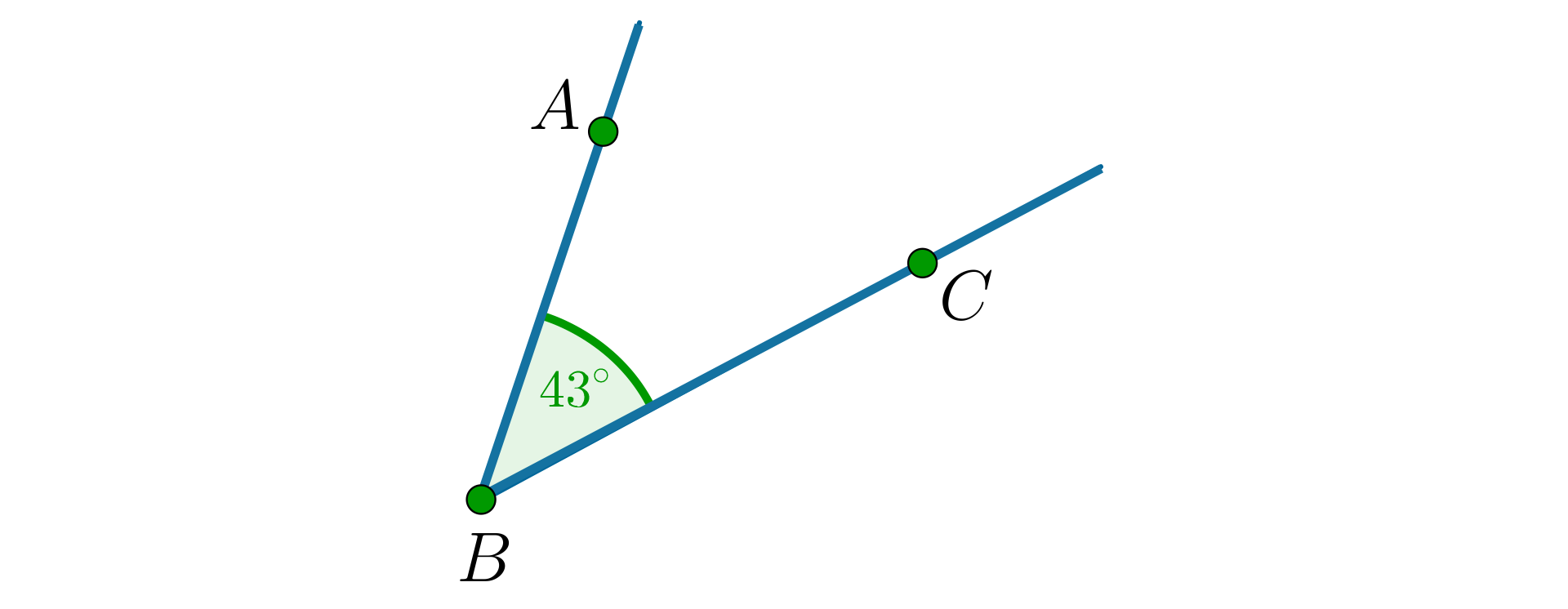
Ten kąt to kąt lub . Środkowa litera zawsze oznacza wierzchołek kąta. Słowo kąt możemy zapisać symbolicznie .
Zapis oznacza kąt .
Zapis oznacza miarę kąta . Jeżeli kąt ma miarę stopni, możemy to zapisać tak: .
Instrukcja rysowania kąta .
Zaznaczamy punkty i oznaczamy je , , .
RC5MjlnYEBC5f1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Rysujemy półproste o początku w punkcie każda.
RVI6JvfaJ0Z891 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Zaznaczamy łukiem jeden z kątów.
R1V4C89BLSGWs1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Mierzymy kąt i wpisujemy jego miarę.
Rr5ai4Td4LaXd1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Kąt wklęsły jest to kąt płaski większy od kąta półpełnego oraz mniejszy od kąta pełnego.
Miara kąta wklęsłego: .
Wyznaczamy kąt wklęsły o mierze .
Konstrukcja będzie polegała na narysowaniu kąta półpełnego oraz kąta, którego miara jest równa różnicy między kątem wklęsłym a półpełnym.
Zaczynamy od wyznaczenia wspomnianej różnicy miary kątów. Zatem .
Rysujemy półprostą i zaznaczamy kąt półpełny.

Korzystamy z kątomierza ustawiając go tak, aby początek półprostej pokrywał się z wyróżnionym punktem kątomierza oraz prosta przechodziła przez punkt odpowiadający zeru na podziałce kątomierza. Na zewnętrznej skali kątomierza odszukujemy liczbę i zaznaczmy odpowiadający jej punkt.

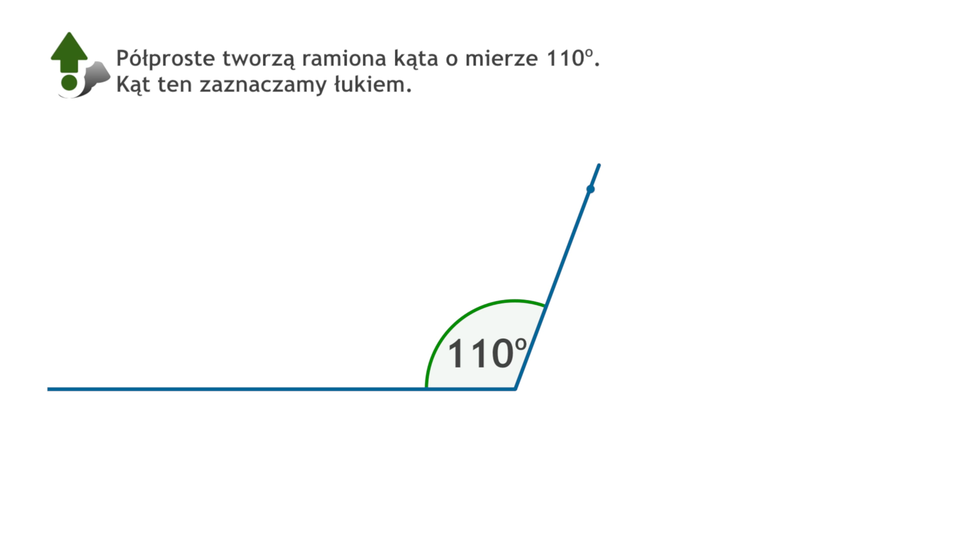
4. Rysujemy półprostą przechodzącą przez ten punkt tak, aby jej początek pokrywał się z początkiem pierwszej półprostej. Półproste tworzą ramiona kąta o mierze . Kąt ten zaznaczamy łukiem. Otrzymany kąt jest kątem wklęsłym.

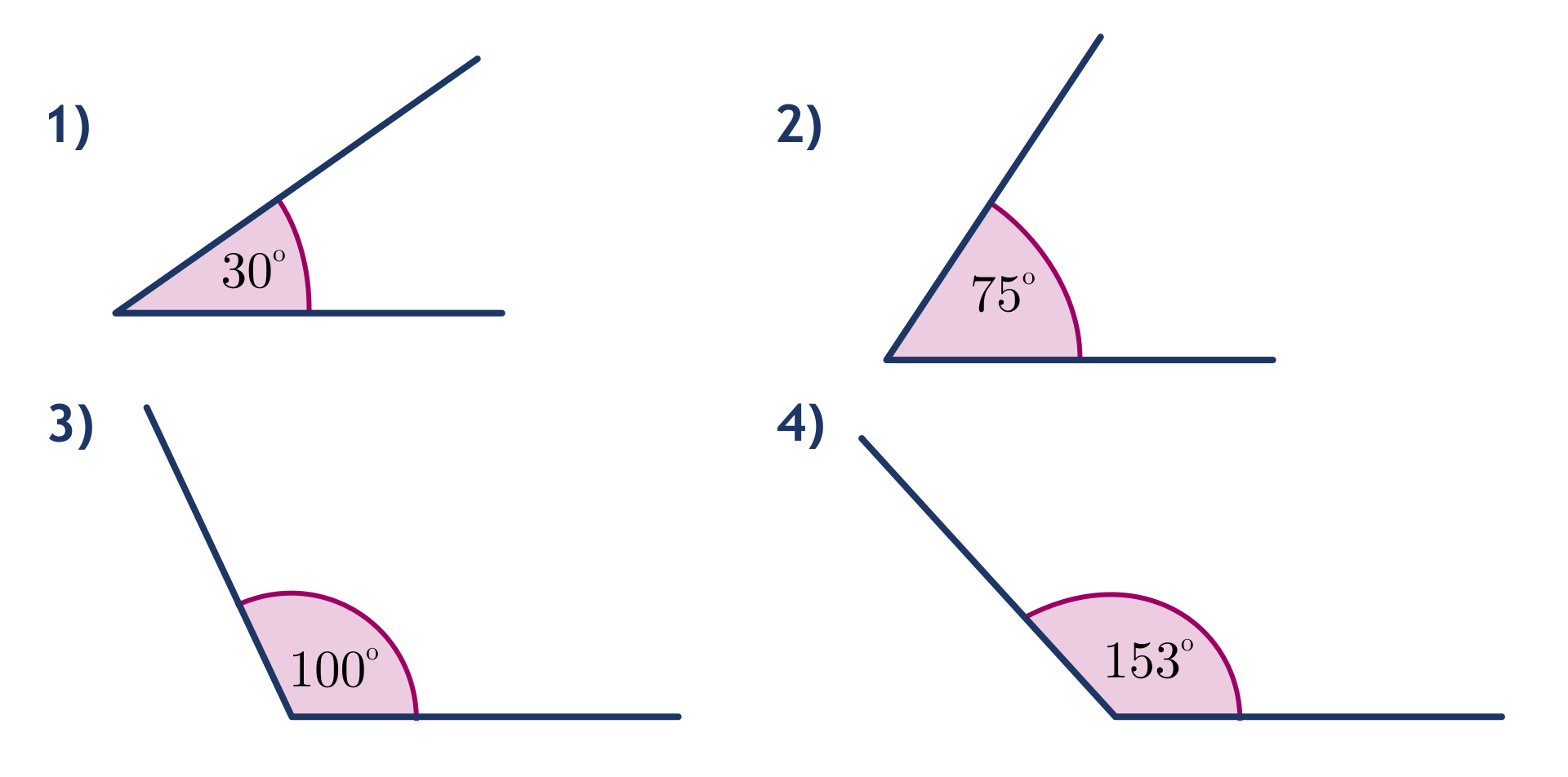
Narysuj ramiona wskazanego kąta znając położenie punktów , , . Zaznacz go łukiem, a następnie zmierz go i odczytaj jego miarę.
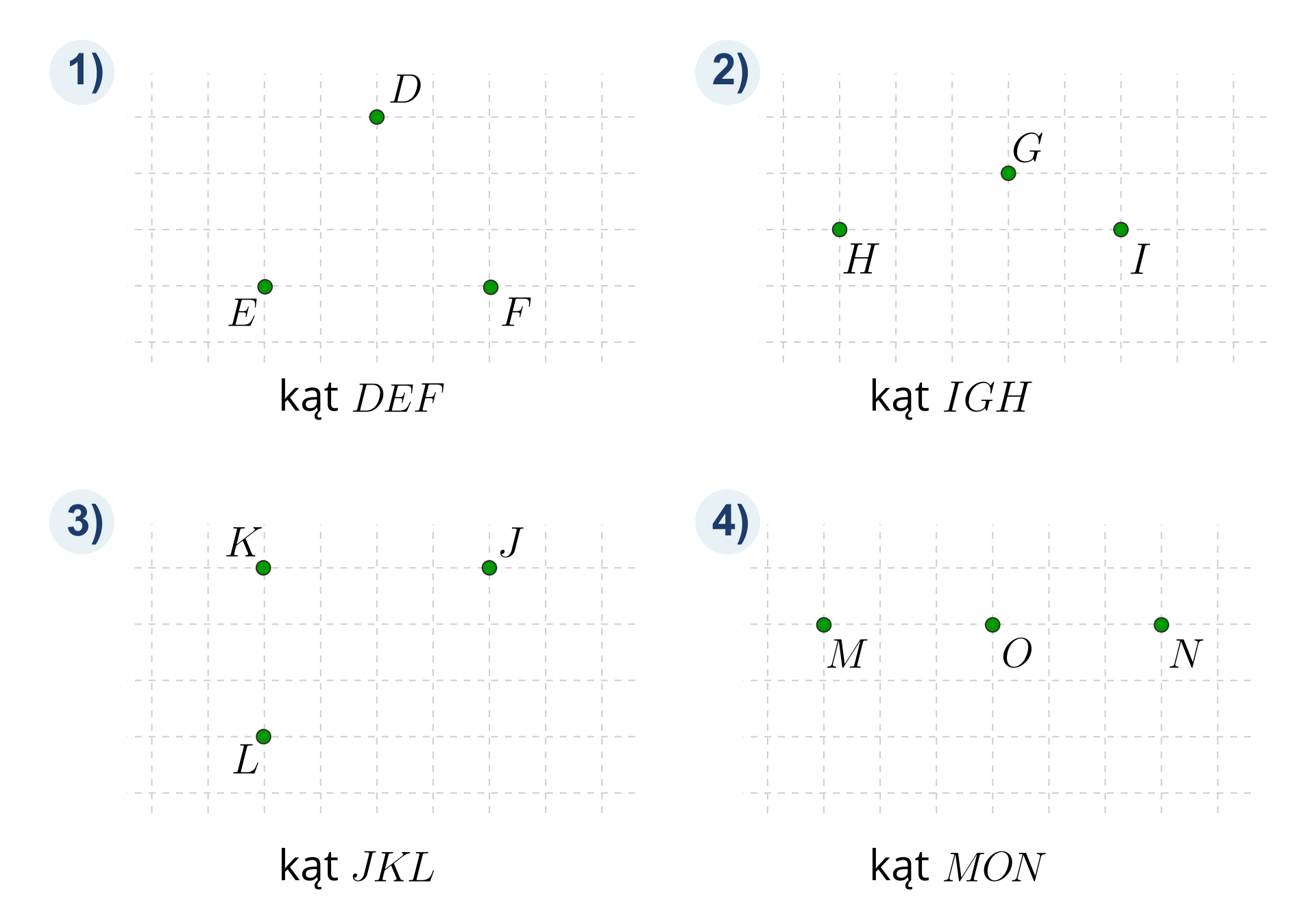
Narysuj kąt o mierze:
,
,
,
.
Narysuj kąt o mierze:
,
,
,
.
Skorzystaj z poniższego szkicownika.
Opisz jak narysować kąt o mierze:
,
,
,
.
Narysuj na kartce kąt o podanej mierze.
Opisz, jak narysować kąt o podanej mierze:
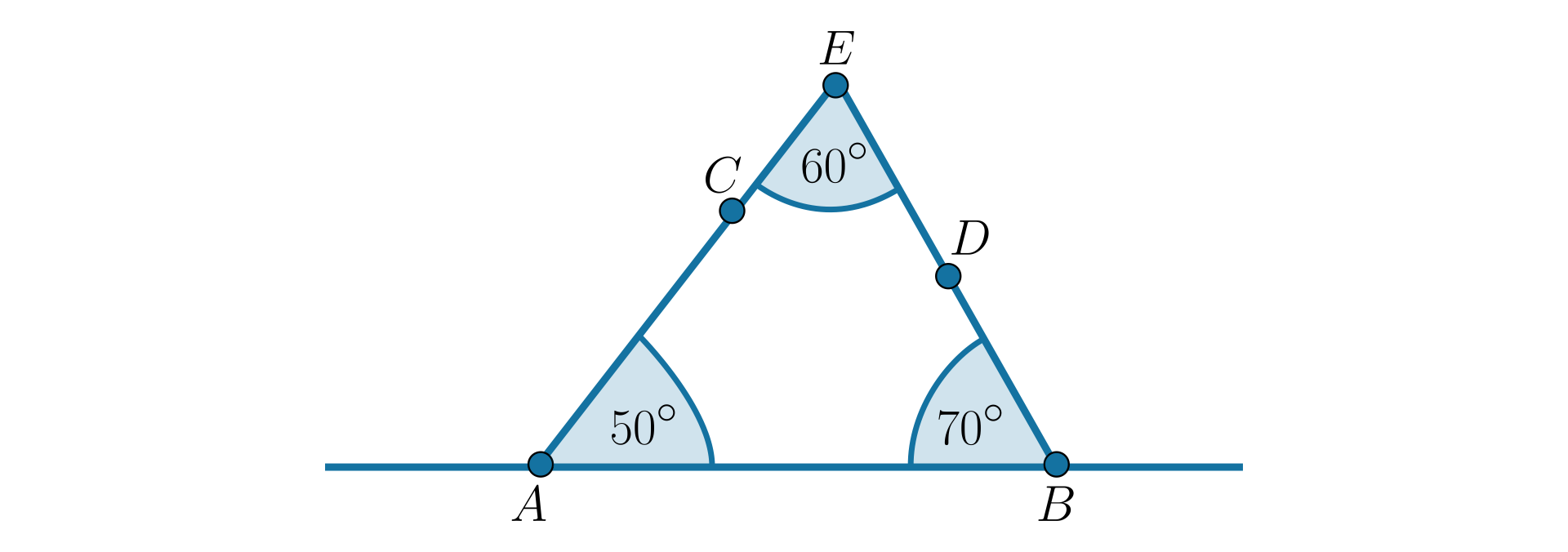
Narysuj prostą i zaznacz na niej dwa punkty i . Narysuj kąt o mierze , a następnie kąt , który ma . Oba kąty powinny leżeć po tej samej stronie prostej . Oznacz punkt przecięcia ramion i obu kątów literą . Zmierz kąt w powstałym trójkącie.
Narysuj kąt o mierze:
,
,
.
Skorzystaj z poniższego szkicownika.
Opisz, jak narysować kąt o mierze:
,
,
.
Narysuj na kartce kąt o podanej mierze.
Opisz, jak narysować kąt o podanej mierze:
Narysuj na kartce trójkąt, w którym dwa kąty mają podane miary.
i
i
i
Trójkąt prostokątny ma jeden z kątów równy mierze 1. wklęsły, 2. ostry, 3. jeden, 4. rozwarty, 5. , 6. trzy, 7. prostym, 8. , 9. dwa nazywany kątem1. wklęsły, 2. ostry, 3. jeden, 4. rozwarty, 5. , 6. trzy, 7. prostym, 8. , 9. dwa.
Trójkąt zbudowany z kątów , oraz zawiera 1. wklęsły, 2. ostry, 3. jeden, 4. rozwarty, 5. , 6. trzy, 7. prostym, 8. , 9. dwa kąty ostre i kąt 1. wklęsły, 2. ostry, 3. jeden, 4. rozwarty, 5. , 6. trzy, 7. prostym, 8. , 9. dwa.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DUz18dm0u
1. Odczytujemy miarę kąta w stopniach. , 2. Ustawiamy kątomierz tak, aby jedno z ramion kąta przechodziło przez zero na skali kątomierza., 3. Znajdujemy na kątomierzu punkt w kształcie litery T., 4. Drugie ramie wskazuje miarę kąta na skali kątomierza., 5. Umieszczamy punkt w kształcie litery T w wierzchołku kąta.
1. Odczytujemy miarę kąta w stopniach. , 2. Ustawiamy kątomierz tak, aby jedno z ramion kąta przechodziło przez zero na skali kątomierza., 3. Znajdujemy na kątomierzu punkt w kształcie litery T., 4. Drugie ramie wskazuje miarę kąta na skali kątomierza., 5. Umieszczamy punkt w kształcie litery T w wierzchołku kąta.
1. Odczytujemy miarę kąta w stopniach. , 2. Ustawiamy kątomierz tak, aby jedno z ramion kąta przechodziło przez zero na skali kątomierza., 3. Znajdujemy na kątomierzu punkt w kształcie litery T., 4. Drugie ramie wskazuje miarę kąta na skali kątomierza., 5. Umieszczamy punkt w kształcie litery T w wierzchołku kąta.
1. Odczytujemy miarę kąta w stopniach. , 2. Ustawiamy kątomierz tak, aby jedno z ramion kąta przechodziło przez zero na skali kątomierza., 3. Znajdujemy na kątomierzu punkt w kształcie litery T., 4. Drugie ramie wskazuje miarę kąta na skali kątomierza., 5. Umieszczamy punkt w kształcie litery T w wierzchołku kąta.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.