6. Kąty przyległe i wierzchołkowe
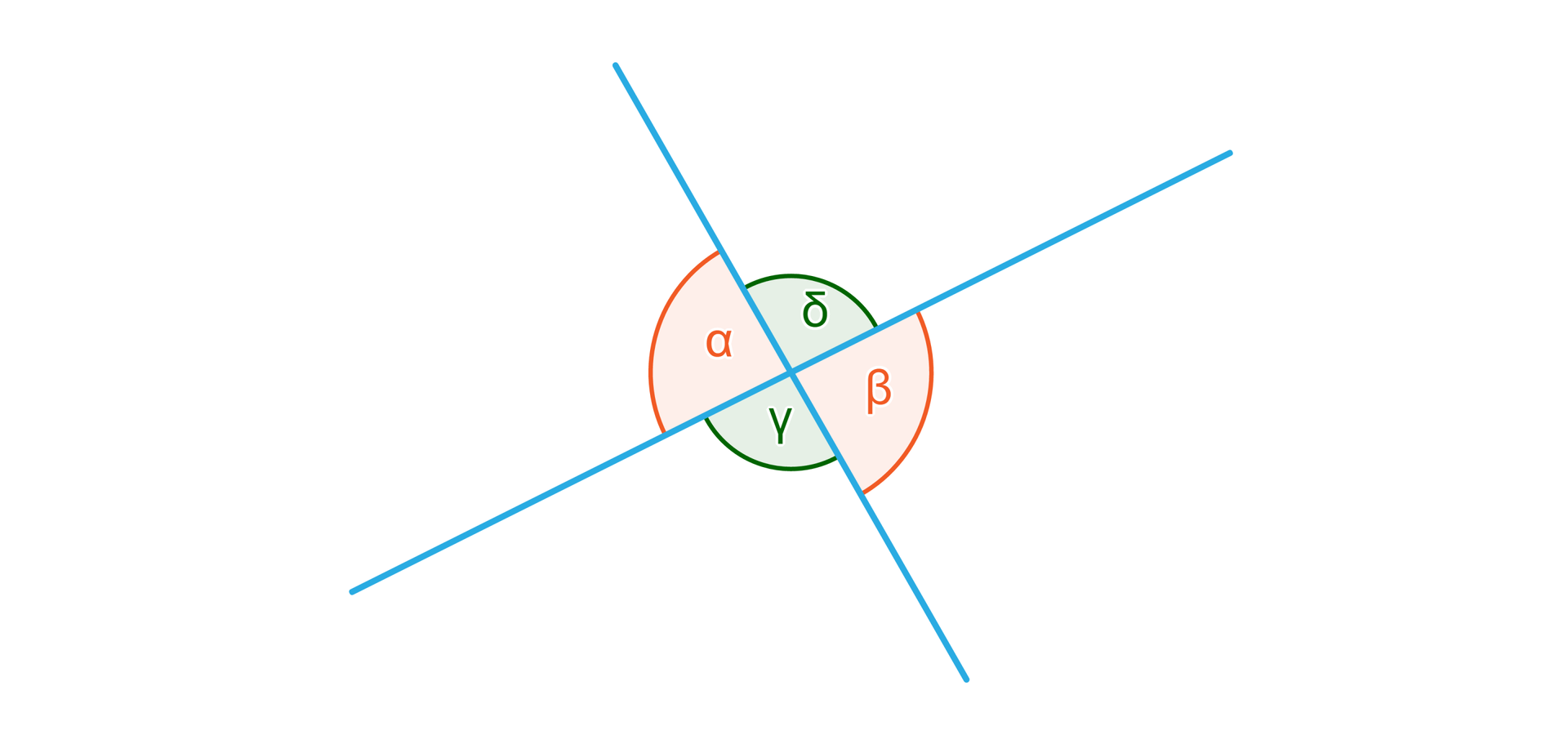
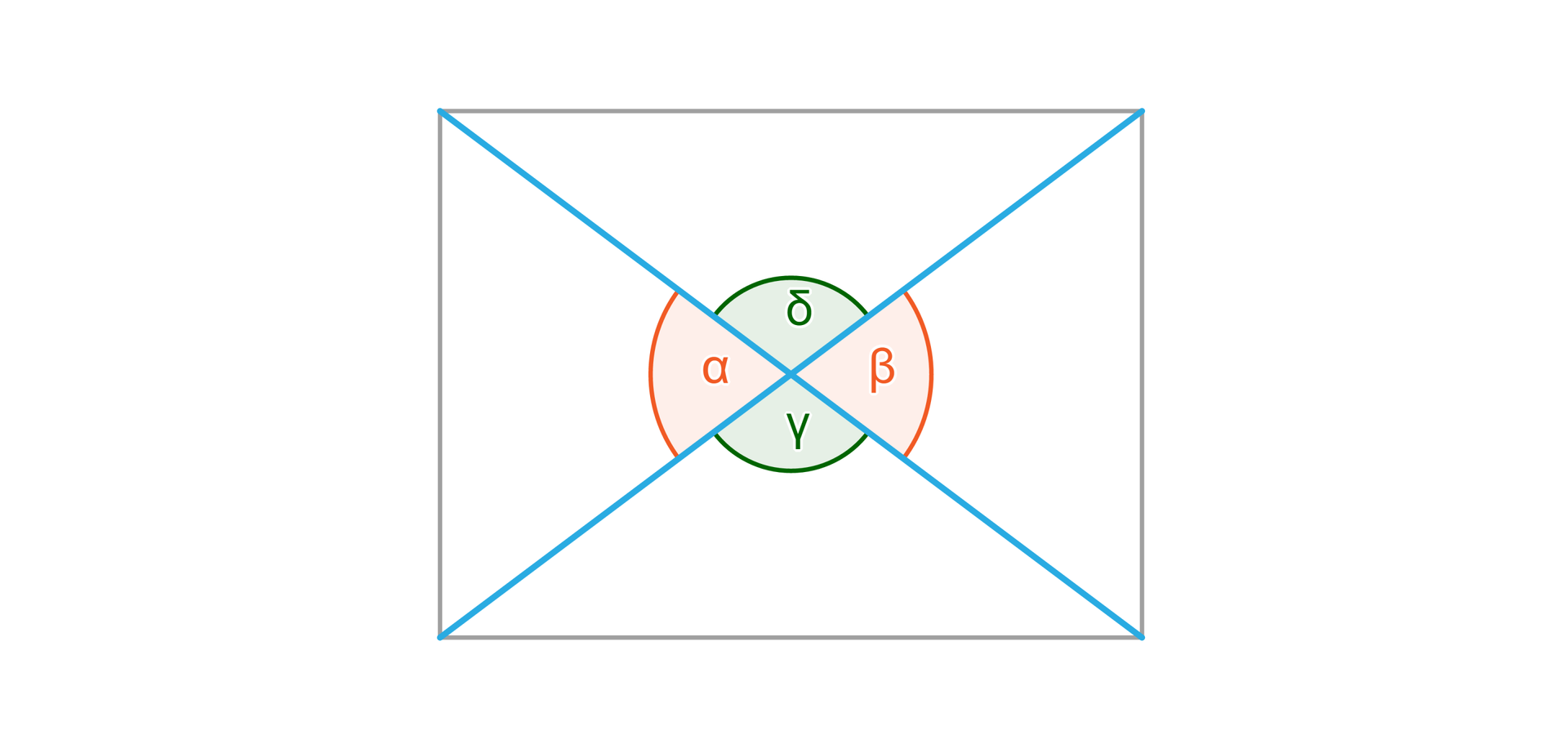
Dwie przecinające się proste wyznaczają cztery kąty. Takie sytuacje spotykamy wokół nas, np. dwie przecinające się ścieżki, dwie krzyżujące się ulice, dwa kije leżące na sobie. Również przekątne w czworokącie wypukłym przecinają się i wyznaczają cztery kąty.
Kąty przyległe
Dwa kąty wypukłe, które mają jedno ramię wspólne, a pozostałe ramiona tworzą prostą, nazywamy kątami przyległymi.

Lena i Milena miały zmierzyć za pomocą kątomierza narysowany kąt. Zapoznaj się z animacją, aby zobaczyć jak sobie poradziły z tym zadaniem.

Film dostępny pod adresem /preview/resource/R1MdTxNyFgxPF
Animacja przedstawia w jaki sposób należy mierzyć kąty przyległe.
Zapoznaj się z poniższym apletem.
Zapoznaj się z opisem poniższej animacji.
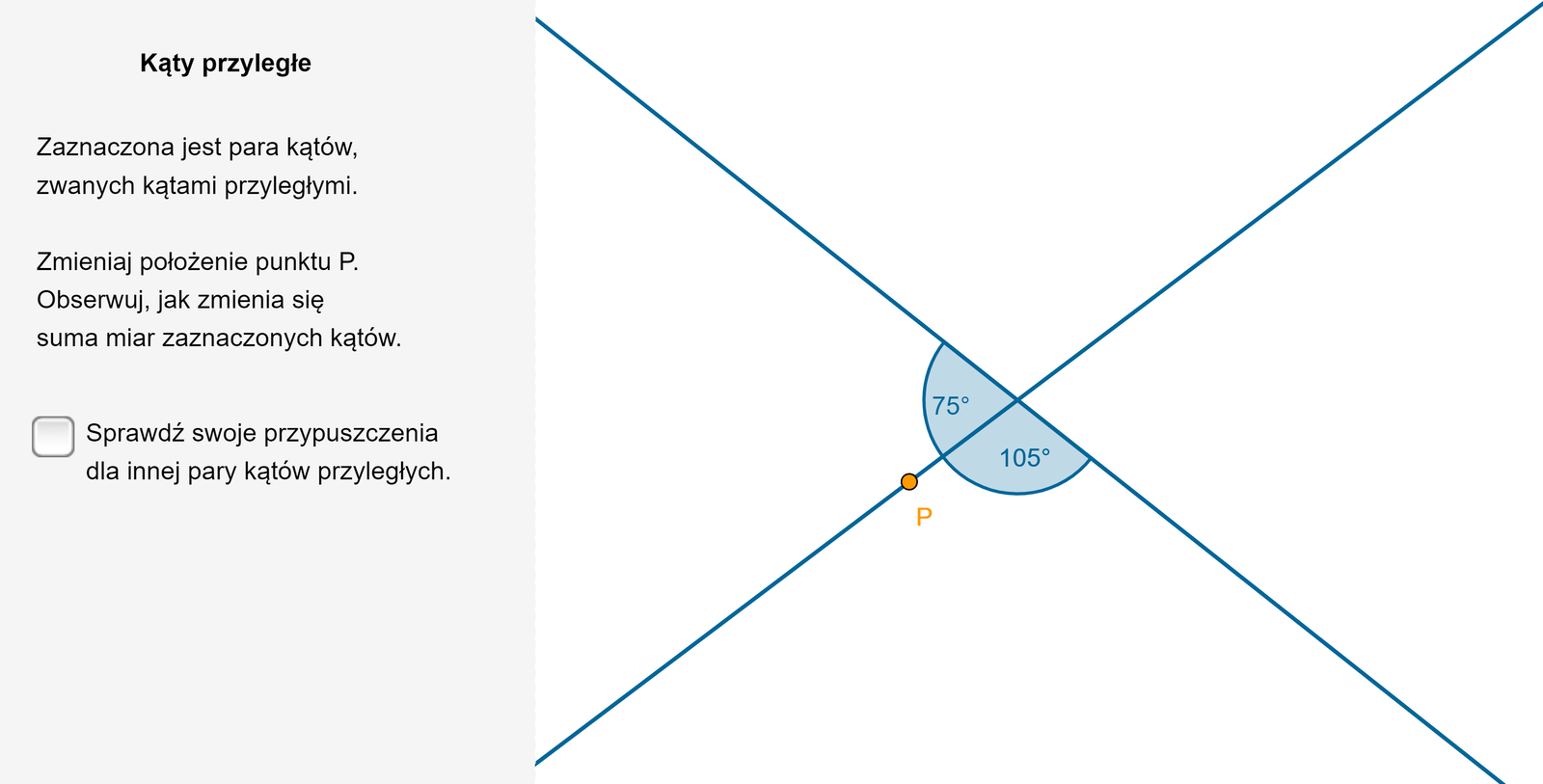
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DU5NmRrS1
Suma miar kątów przyległych jest równa .

Zapoznaj się z poniższym apletem.
Zapoznaj się z opisem poniższej animacji.
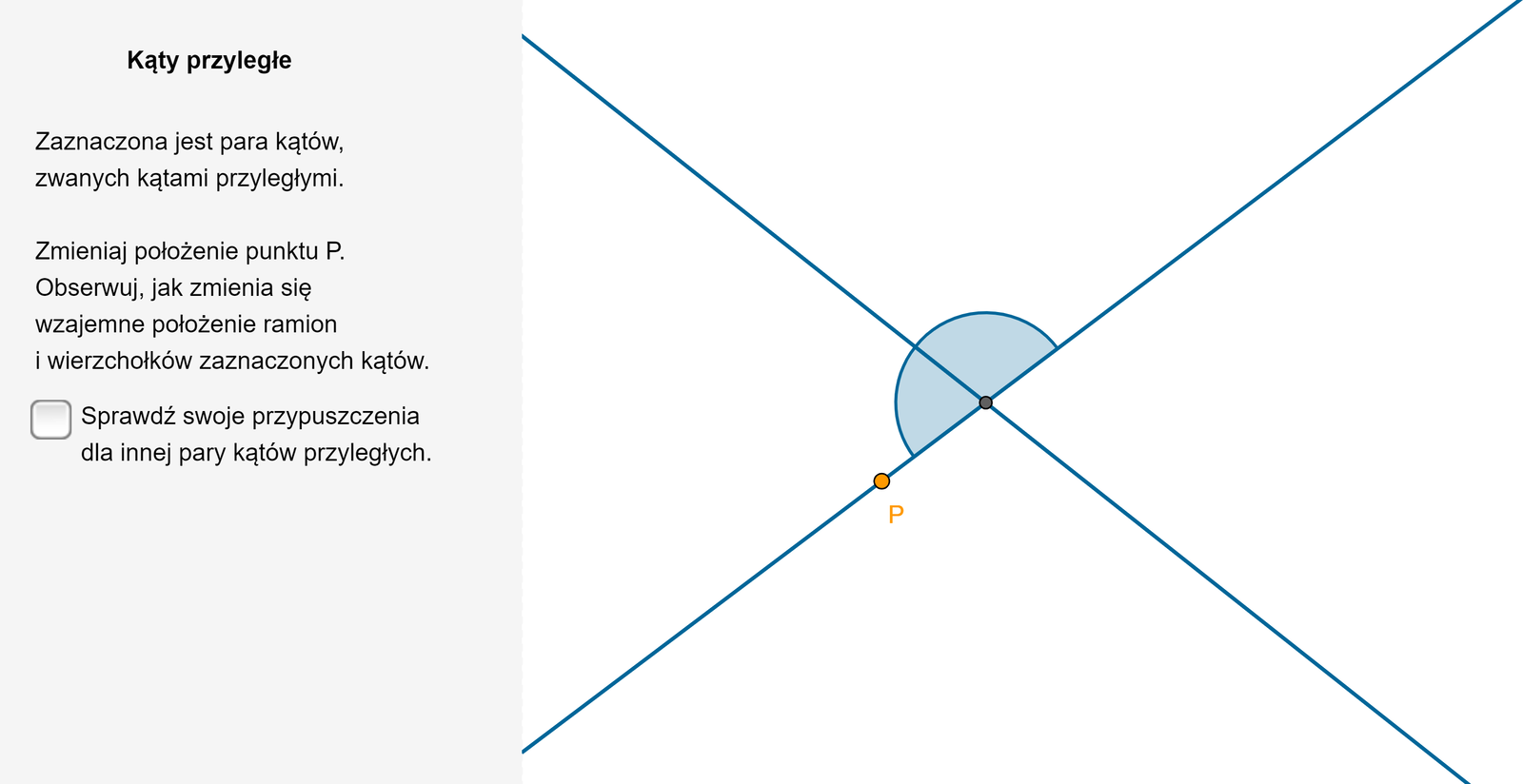
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DU5NmRrS1
Kąty przyległe mają wspólny wierzchołek.
Kąty wierzchołkowe
Kąty wypukłe, których ramiona uzupełniają się do prostych, nazywamy kątami wierzchołkowymi.

Zapoznaj się z animacją, aby dowiedzieć sie więcej o kątach wierzchołkowych.

Film dostępny pod adresem /preview/resource/R1BeKu0cUPYw1
Animacja przedstawia w jaki sposób należy mierzyć kąty wierzchołkowe.
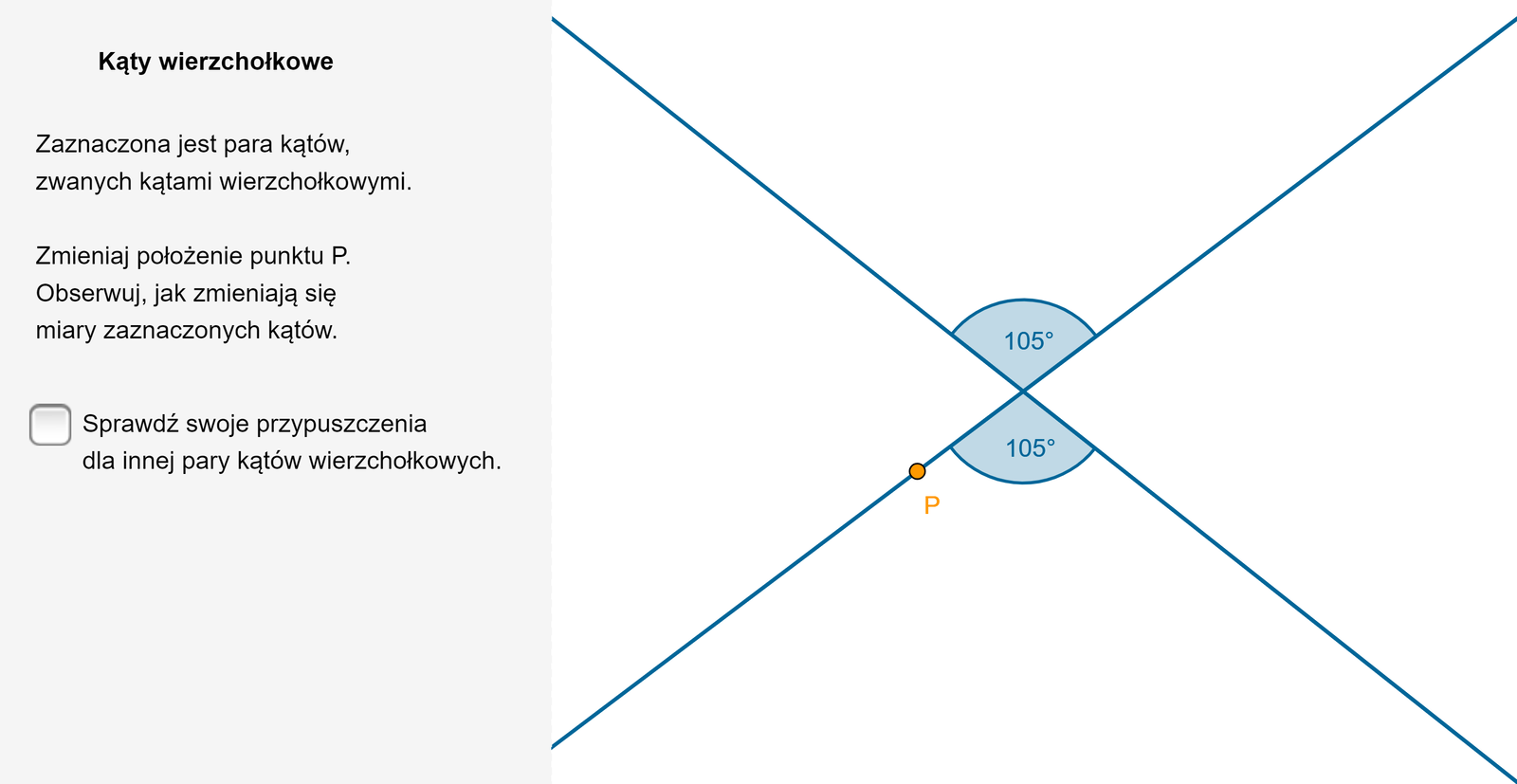
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DU5NmRrS1
Kąty wierzchołkowe mają równe miary.

Przeciągnij i upuść.
45˚, 180˚, 360˚, 0˚, 90˚
Jeśli kąty przyległe są sobie równe, to każdy z nich ma miarę równą ............ stopni.
Jeden z kątów przyległych ma miarę o 56˚ mniejszą od miary kąta półpełnego. Jaka jest miara drugiego z tych kątów?
Odp.: Drugi kąt ma miarę ............ °.
Trzy proste przecinające się w jednym punkcie podzieliły płaszczyznę na sześć kątów.

Spośród kątów - pary kątów wierzchołkowych to: Możliwe odpowiedzi: 1. i , 2. i , 3. i , 4. i , 5. i , 6. i
Rysunek przedstawia kąty ostre i rozwarte.

- Kąty i to kąty wierzchołkowe.
- Kąty i mają taką samą miarę.
- Kąt jest przyległy do kąta .
- Suma kątów i wynosi .
- Kąty i nie są kątami wierzchołkowymi.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.