R1KArxESX7CXy
Rysunek przedstawia boisko. Na końcu boiska jest kosz do koszykówki. Napis: Wielokąty, koła i okręgi.

Wielokąty, koła i okręgi

Źródło: Santiago Pagnotta, dostępny w internecie: https://pexels.com/, domena publiczna.

5. Równoległobok i jego własności

Rrnv14LNXNJJr
Ilustracja przedstawia szklany budynek w kształcie równoległoboku.
Źródło: KarstenBergmann, dostępny w internecie: pixabay.com, domena publiczna.

Na zdjęciu przedstawiony jest biurowiec w porcie w Hamburgu. Jest to sześciokondygnacyjny budynek o charakterystycznym wyglądzie, wystający nad wodę jak burta statku. Główna ściana tego budynku to równoległobok o długości 134 metrów i wysokości 25 metrów.

W tym materiale przekonasz się, jak dużo ciekawych problemów możesz rozwiązać, dostrzegając własności czworokąta, którego przeciwległe boki są równoległe.

Równoległobok, jego boki i przekątne

Zapoznaj się z poniższym apletem.

Zapoznaj się z opisem poniższego apletu.

RZtcQOJafqRfm11
Animacja przedstawia prostokąt A B C D. Należy tak przemieszczać wierzchołki C i D, aby otrzymany czworokąt miał nadal równoległe boki a nie był prostokątem. Powstałe figury to równoległoboki, wyglądają one jak pochylone prostokąty.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DDAhYK2e1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Równoległobok
Definicja: Równoległobok

Równoległobok to czworokąt, który ma dwie pary boków równoległych.

RI7vX6ADXfmLc1
Rysunek równoległoboku A B C D. Zapis: AB równoległe do DC i AD równoległe do BC.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R14YQfkyYh64f1
Animacja przedstawia sposób konstrukcji równoległoboku. Zaczynamy od narysowania odcinka A B, który stanowi podstawę równoległoboku. Rysujemy drugi odcinek o początku w punkcie A, który jest nachylony względem podstawy o dowolny kąt, oznaczamy go jako A C. Konstruujemy prostą równoległą do podstawy A B przechodzącą przez punkt C oraz prostą równoległą do odcinka A C przechodzącą przez punkt B. Punkt przecięcia tych prostych oznaczamy jako punkt D. W ten sposób otrzymaliśmy równoległobok A B C D.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

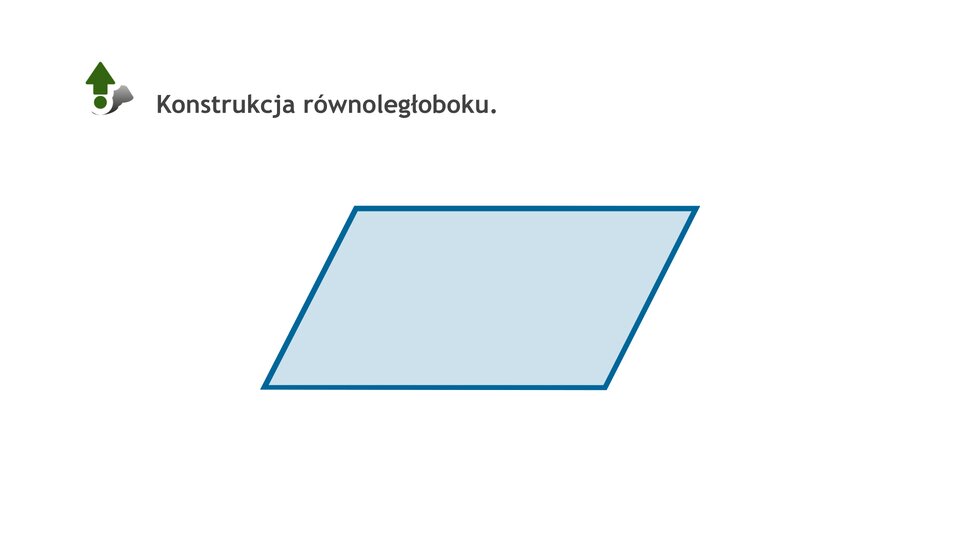
Film dostępny pod adresem /preview/resource/R14YQfkyYh64f

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia sposób konstrukcji równoległoboku. Zaczynamy od narysowania odcinka A B, który stanowi podstawę równoległoboku. Rysujemy drugi odcinek o początku w punkcie A, który jest nachylony względem podstawy o dowolny kąt, oznaczamy go jako A C. Konstruujemy prostą równoległą do podstawy A B przechodzącą przez punkt C oraz prostą równoległą do odcinka A C przechodzącą przez punkt B. Punkt przecięcia tych prostych oznaczamy jako punkt D. W ten sposób otrzymaliśmy równoległobok A B C D.

1
Polecenie 1

Dokończ rysunek równoległoboku.

RkDVN8ncK4QMA1
Animacja ilustruje powstawanie równoległoboków, gdy dane są trzy wierzchołki P, Q, R tworzące boki TP i PQ oraz dowolnie położony punkt R. Należy umieścić punkt R tak, aby powstał równoległobok P Q R T. Kolejno dane są wierzchołki N, K, L i punkt M. Należy utworzyć równoległobok K LM N. Następnie podane są wierzchołki A, B, C i punkt D. Należy utworzyć równoległobok A B C D.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DDAhYK2e1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1kQMSkBw8a4t
Wybierz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Równoległobok ma wszystkie boki równej długości., 2. Równoległobok ma dwie pary boków równej długości., 3. Pary boków, które leżą w równoległoboku są równoległe., 4. Pary boków, które leżą w równoległoboku są prostopadłe.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Własności równoległoboku

Zwróć uwagę na kąty w równoległoboku.

Rzxs8LW0ADmqa1
Animacja przedstawia równoległobok oraz jego własności.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

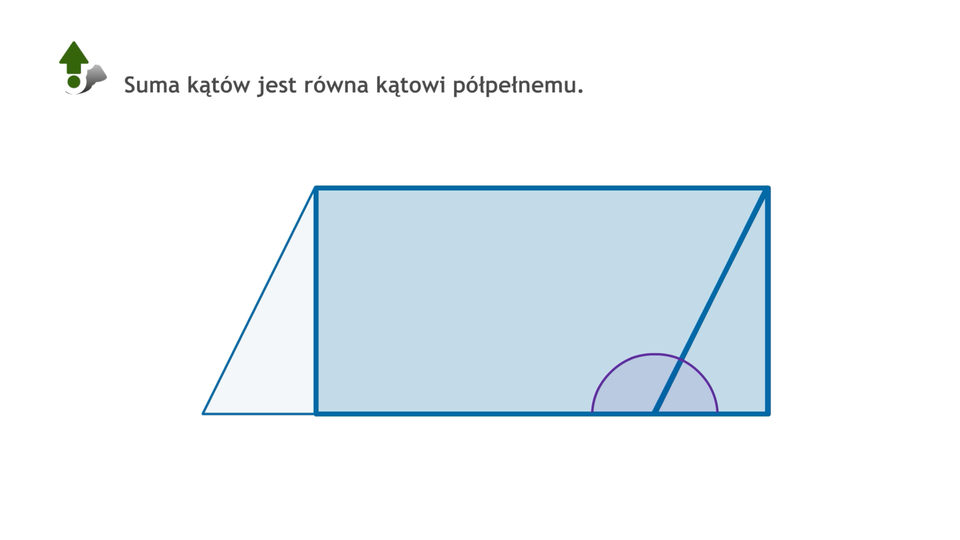
Film dostępny pod adresem /preview/resource/Rzxs8LW0ADmqa

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia równoległobok oraz jego własności.

1
Ważne!

Własności równoległoboku
1. Równoległobok ma dwie pary boków: równoległych i równej długości.

R1GY0D8zs2Zv71
Na rysunku widzimy równoległobok ABCD. Widzimy, że pary naprzeciwległych boków mają takie same długości i są do siebie równoległe.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RNnrDrUYa7yOi1
Animacja prezentuje równoległobok A B C D o bokach a, b. Należy poruszać wierzchołkami A lub B równoległoboku i obserwować jak zmieniają się względem siebie jego przeciwległe boki. Następnie pokazuje się odpowiedź: AB równoległe do DC i AD równoległe do BC.

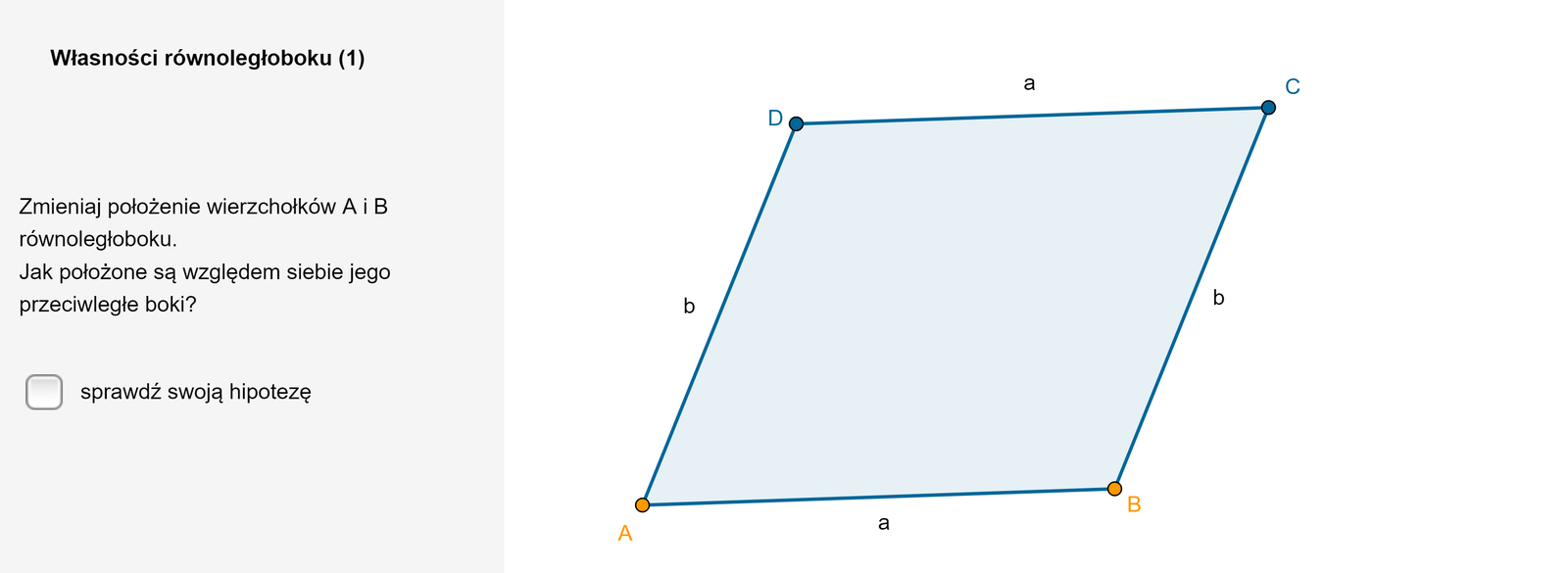
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DDAhYK2e1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

2. Przeciwległe kąty mają równe miary. Suma miar sąsiednich kątów wynosi 180°.

RurkwrkmL29oW1
Rysunek równoległoboku. Zaznaczone kąty alfa i beta leżące przy sąsiednim boku. Zapis: alfa + beta =180 stopni.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R15r7J27zDhVd1
Animacja prezentuje równoległobok A B C D, w którym zaznaczone są kąty alfa i beta leżące przy sąsiednim boku. Poruszając wierzchołkami A lub B równoległoboku należy obserwować miary kątów przeciwległych i kątów sąsiednich. Kąty przeciwległe równoległoboku mają te same miary. Suma kątów sąsiednich wynosi 180 stopni, czyli alfa + beta = 180 stopni.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DDAhYK2e1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

3. Przekątne dzielą się na połowy.

RptPBGecPA2Eg1
Rysunek równoległoboku A B C D. Poprowadzone przekątne przecinają się punkcie O. Zapis: długości AO =OC i DO =OB.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1M2N3iTcHFdy1
Animacja prezentuje równoległobok A B C D, którego przekątne przecinają się w punkcie Q. Poruszając punktami A i B równoległoboku należy sprawdzić, czym jest punkt Q przecięcia przekątnych. Punkt przecięcia przekątnych Q jest środkiem każdej z przekątnych.

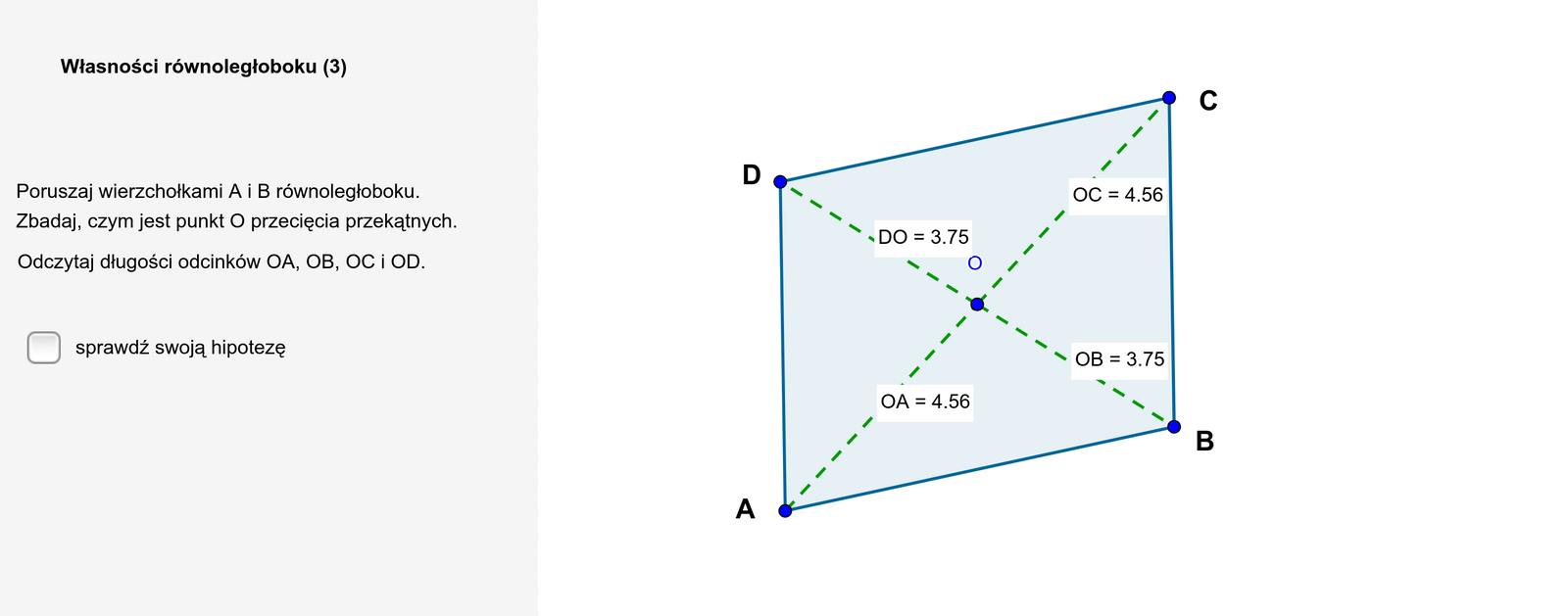
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DDAhYK2e1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wysokość równoległoboku

R1EZv9OlJb7vq1
Animacja przedstawia które odcinki możemy nazywać wysokościami równoległoboku.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

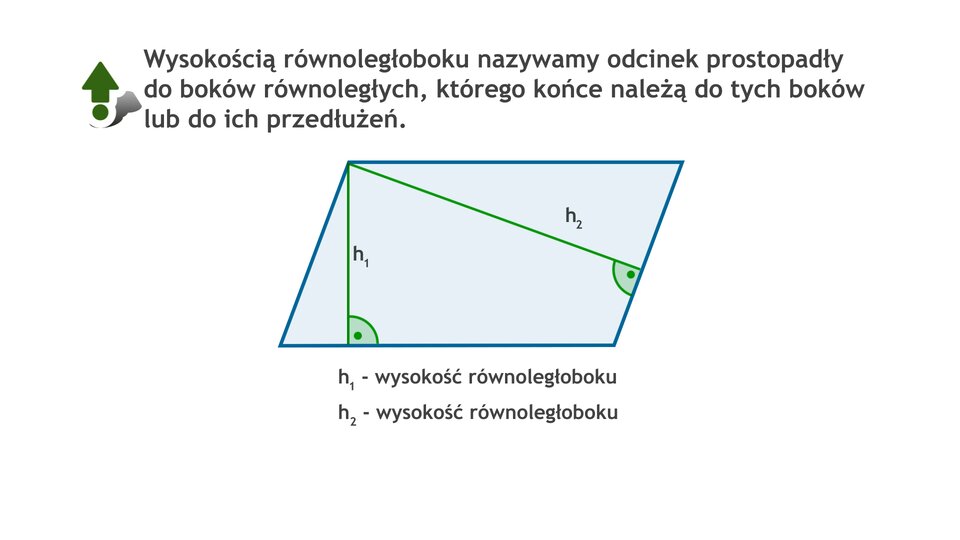
Film dostępny pod adresem /preview/resource/R1EZv9OlJb7vq

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia które odcinki możemy nazywać wysokościami równoległoboku.

Wysokość równoległoboku
Definicja: Wysokość równoległoboku

Wysokością równoległoboku nazywamy odcinek łączący dwa jego równoległe boki (lub ich przedłużenia) i prostopadły do nich.

Zauważ, że każdy odcinek łączący dwa równoległe boki tego samego równoległoboku i prostopadły do nich ma tę samą długość.

RRC1Nup2BkdUS
Rysunek przedstawia równoległobok z poprowadzonymi kilkoma wysokościami. Pierwsze trzy z nich oznaczone literką h z indeksem dolnym 1, h z indeksem dolnym 2 oraz h z indeksem dolnym 3 poprowadzone są na dłuższy bok równoległoboku, natomiast wysokości oznaczone jako g z indeksem dolnym 1, g z indeksem dolnym 2 oraz g z indeksem dolnym 3,poprowadzone są na drugi, krótszy bok, który nie jest równoległy do pierwszego boku.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ważne!

Ponieważ każdy równoległobok ma dwie pary boków równoległych, ma także dwie wysokości. Czasem są to odcinki tej samej długości, a czasem różnej.

Ćwiczenie 1

Na rysunku wyznaczono dwa sąsiednie boki równoległoboku. Dokończ rysunek tego równoległoboku.

  1. R1U3SnnOgW9K41
    Rysunek dwóch sąsiednich boków równoległoboku.
    Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

  2. RzkLTUkhvazZp1
    Rysunek dwóch sąsiednich boków równoległoboku.
    Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

  3. RViXbM8OZuSeC1
    Rysunek dwóch sąsiednich boków równoległoboku.
    Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RFNMHrE71DV4a
Szkicownik.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Dany jest równoległobok ABCD, w którym boki AB i CD leżą na przeciwko siebie. Podaj wszystkie pary boków równoległych w tym równoległoboku.

R1DLoleayuDh5
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 2

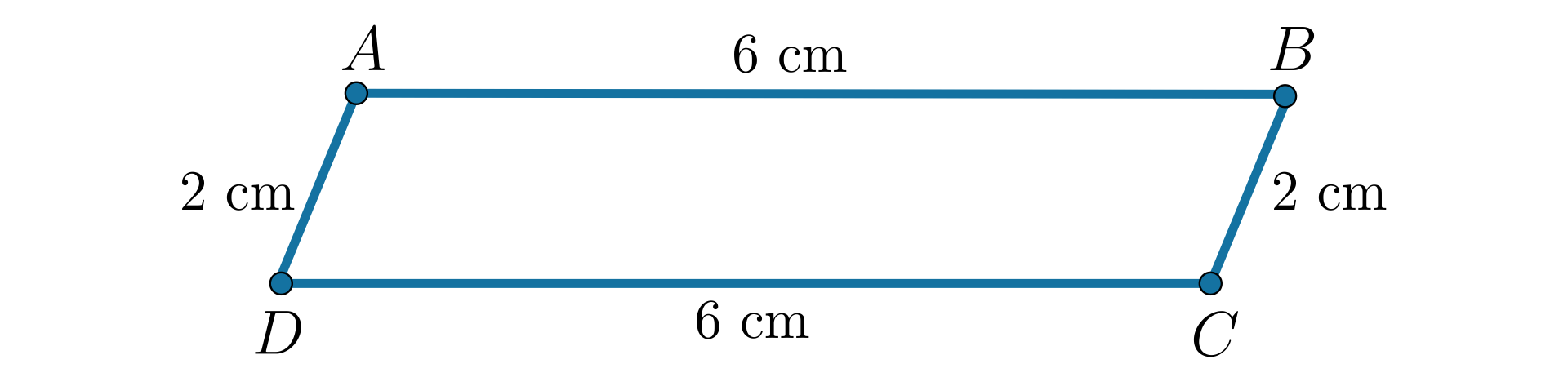
Narysuj równoległobok ABCD, w którym sąsiednie boki AB i AD mają odpowiednio długości 6 cm i 2 cm. Zmierz pozostałe boki równoległoboku.

RYUgBRlVcIkV9
Szkicownik.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R12hYbAr3I4q31
Uzupełnij zdania, przeciągając w luki odpowiednie liczby i słowa, lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Odpowiedź: Bok BC ma długość 1. 6, 2. 2, 3. równe, 4. 3, 5. 4, 6. różne cm, a długość boku CD wynosi 1. 6, 2. 2, 3. równe, 4. 3, 5. 4, 6. różne cm.
Te boki równoległoboku, które są równoległe, mają 1. 6, 2. 2, 3. równe, 4. 3, 5. 4, 6. różne długości.

Narysuj równoległobok ABCD, w którym sąsiednie boki AB i AD mają odpowiednio długości 6 cm i 2 cm. Zmierz pozostałe boki równoległoboku.
Wybierz.

równe, 6, różne, 4, 2, 3

Bok BC ma długość .............. cm, a długość boku CD wynosi .............. cm.
Te boki równoległoboku, które są równoległe mają .............. długości.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1Y0godpIzDiX
Ćwiczenie 2
W równoległoboku ABCD sąsiednie boki AB i AD mają odpowiednio długości 6 cm i 2 cm. Jaką długość mają pozostałe boki równoległoboku? Uzupełnij zdania, przeciągając w luki odpowiednie liczby i słowa, lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Odpowiedź: Bok BC ma długość 1. równe, 2. 3, 3. 2, 4. różne, 5. 4, 6. 6 cm, a długość boku CD wynosi 1. równe, 2. 3, 3. 2, 4. różne, 5. 4, 6. 6 cm.
Te boki równoległoboku, które są równoległe, mają 1. równe, 2. 3, 3. 2, 4. różne, 5. 4, 6. 6 długości.

Narysuj równoległobok ABCD, w którym sąsiednie boki AB i AD mają odpowiednio długości 6 cm i 2 cm. Zmierz pozostałe boki równoległoboku.
Wybierz.

równe, 6, różne, 4, 2, 3

Bok BC ma długość .............. cm, a długość boku CD wynosi .............. cm.
Te boki równoległoboku, które są równoległe mają .............. długości.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 3
R1LdbZLvyubg31
Oblicz obwód równoległoboku, w którym sąsiednie boki mają długości 7 cm i 5 cm. Uzupełnij odpowiedź, wpisując w lukę odpowiednią liczbę. Odpowiedź: Obwód tego równoległoboku wynosi Tu uzupełnij cm.

Oblicz obwód równoległoboku, w którym sąsiednie boki mają długości 7 cm i 5 cm.

Odp.: Obwód tego równoległoboku wynosi ............ cm.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 4
RzVWLAZwpvz8I1
Oblicz obwód równoległoboku, w którym jeden bok ma długość 8 cm, a drugi jest od niego o 2,5 cm dłuższy. Uzupełnij odpowiedź, wpisując w lukę odpowiednią liczbę. Odpowiedź: Obwód tego równoległoboku wynosi Tu uzupełnij cm.

Oblicz obwód równoległoboku, w którym jeden bok ma długość 8 cm, a drugi jest od niego o 2,5 cm dłuższy.

Odp.: Obwód tego równoległoboku wynosi ............ cm.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
1
Ćwiczenie 5

Zmieniaj położenie wierzchołków S, F i U. Obserwuj, jak zmieniają się długości przekątnych i pod jakim kątem przecinają się przekątne.

RUk29mF7rub301
Animacja przedstawia równoległobok F U K S z poprowadzonymi przekątnymi. Przekątne przecinają się w punkcie O. Poruszając wierzchołkiem S (figurą zawsze jest równoległobok) należy obserwować długości boków równoległoboku oraz długości jego przekątnych. Zauważamy, że gdy równoległobok jest prostokątem, to jego przekątne są tej samej długości a boki różnej. Dla kwadratu kąt między przekątnymi jest prosty i są one równej długości. Punkt O przecięcia przekątnych jest dla każdej przekątnej równoległoboku jej środkiem.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DDAhYK2e1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RiivyBOVHD4Ma
Uzupełnij zdania, przeciągając w luki odpowiednie słowa, lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Przekątne w równoległoboku, który nie jest prostokątem, są 1. równej, 2. są, 3. równe, 4. równe, 5. różnej, 6. nie są, 7. różne, 8. różne długości. Jeżeli równoległobok stanie się prostokątem, to jego przekątne będą miały 1. równej, 2. są, 3. równe, 4. równe, 5. różnej, 6. nie są, 7. różne, 8. różne długości. W równoległoboku o sąsiednich bokach różnej długości przekątne 1. równej, 2. są, 3. równe, 4. równe, 5. różnej, 6. nie są, 7. różne, 8. różne prostopadłe.W każdym równoległoboku punkt przecięcia przekątnych dzieli je na dwie 1. równej, 2. są, 3. równe, 4. równe, 5. różnej, 6. nie są, 7. różne, 8. różne części.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 6

W równoległoboku FUKS przekątne przecinają się w punkcie O. Punkt O dzieli obie przekątne na dwie części, których długości zmierzono.

R11cVvWe06E921
"Rysunek równoległoboku F U K S, którego przekątne przecinają się punkcie O. Zapis: długość: SO=5,66, OU=5,66, FO=3,26 i OK=3,26
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RVfib1yf1ywmf
Uzupełnij zdania, przeciągając w luki odpowiednie słowa, lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Odcinki SO i OU są 1. jednej przekątnej, 2. jest, 3. obu przekątnych, 4. równej, 5. różnej, 6. nie jest, 7. równej, 8. różnej długości. Odcinki FO i OK są 1. jednej przekątnej, 2. jest, 3. obu przekątnych, 4. równej, 5. różnej, 6. nie jest, 7. równej, 8. różnej długości. Punkt O 1. jednej przekątnej, 2. jest, 3. obu przekątnych, 4. równej, 5. różnej, 6. nie jest, 7. równej, 8. różnej środkiem 1. jednej przekątnej, 2. jest, 3. obu przekątnych, 4. równej, 5. różnej, 6. nie jest, 7. równej, 8. różnej.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 7

Narysuj dowolny równoległobok o przekątnych długości

  1. 4 cm i 2 cm,

  2. 3 cm i 5 cm,

  3. 6 cm i 6 cm.

R1cFWHLlsSU03
Szkicownik.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Podaj wymiary przekątnych dowolnych trzech równoległoboków, które nie są prostokątami.

R6TYuWeibn5dg
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 8

Narysuj trzykrotnie taki sam rysunek: kąt o mierze 45°, a na ramionach kąta odcinki o długościach 3 cm i 4 cm. Na każdym rysunku wprowadź oznaczenia, jak poniżej. Dokończ każdy z rysunków tak, by otrzymać równoległobok ABCD, w którym punkt O jest punktem przecięcia przekątnych.

  1. RNPa8nvYiW3t71
    Rysunek kąta C O B.
    Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

  2. Rb2ZPTMgrAAIV1
    Rysunek kąta C A B.
    Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

  3. R15fPv5J2lDsg1
    Rysunek kąta D A C.
    Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RdNrlu1jrR0uG
Szkicownik.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Dany jest kąt o mierze 45°, a na ramionach kąta odcinki o długościach 3 cm i 4 cm. Załóżmy, że wierzchołek tego kąta to punkt przecięcia przekątnych pewnego równoległoboku, a ramiona tego kąta to fragmenty jego przekątnych. Podaj długości przekątnych tego równoległoboku. Czy ten równoległobok jest prostokątem?

R1CiqYLe9LM8x
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 9
R1A7TiirREYur1
Uzupełnij poniższe zdanie, wpisując w luki odpowiednie liczby. Jeżeli jeden z kątów równoległoboku ma miarę 30°, to pozostałe kąty tego równoległoboku, zapisując je w kolejności od największego do najmniejszego, mają miary: Tu uzupełnij°, Tu uzupełnij° i Tu uzupełnij°.

Uzupełnij.

Jeżeli jeden z kątów równoległoboku ma miarę 30°, to

pozostałe kąty tego równoległoboku mają miary: ............ °, ............ ° i ............ °.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 10
R1YYgslIQYpYj
W równoległoboku kąt rozwarty ma miarę 3 razy większą niż kąt ostry. Oblicz miary obu kątów i uzupełnij poniższe zdanie, wpisując w luki odpowiednie liczby. Odpowiedź: Miara kąta ostrego wynosi Tu uzupełnij°, a kąta rozwartego Tu uzupełnij°.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 11

Przekątne równoległoboku MORS przecinają się w punkcie L.

R17lgb3ORDU0X1
Rysunek równoległoboku M O R S. Poprowadzone przekątne przecinają się w punkcie L.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R12JLtRiq5mnH
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Jeżeli bok MO ma długość 7 cm, a bok MS ma długość 5 cm, to obwód równoległoboku wynosi 12 cm., 2. Jeżeli ML=4 cm i LO=3 cm, to suma długości przekątnych równoległoboku wynosi 14 cm., 3. Jeżeli trójkąt ROM jest równoboczny, to kąt ORS ma 120 ° ., 4. Jeżeli ML=LO, to równoległobok MORS jest prostokątem., 5. Jeżeli obwód trójkąta ROM wynosi 20 cm, a obwód trójkąta ROS - 18 cm, to jedna przekątna równoległoboku jest o 2 cm dłuższa od drugiej.

  • Jeżeli bok MO ma długość 7  cm , a bok MS ma długość 5  cm , to obwód równoległoboku
    wynosi 12  cm .
  • Jeżeli | ML | = 4  cm i  | LO = 3  cm , to suma długości przekątnych równoległoboku
    wynosi 14  cm .
  • Jeżeli trójkąt ROM jest równoboczny, to kąt ORS ma 120 ° .
  • Jeżeli ML = | LO | , to równoległobok MORS jest prostokątem.
  • Jeżeli obwód trójkąta ROM wynosi 20  cm , a obwód trójkąta ROS  –   18  cm , to jedna
    przekątna równoległoboku jest o  2  cm dłuższa od drugiej.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1AJremEBpoIc
Ćwiczenie 12
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Każdy prostokąt jest równoległobokiem., 2. Każdy równoległobok jest prostokątem., 3. Każdy równoległobok, w którym przekątne są prostopadłe, jest kwadratem., 4. Każdy równoległobok, w którym wszystkie boki są równej długości, jest kwadratem., 5. Każdy równoległobok, który ma kąt prosty, jest prostokątem.

  • Każdy prostokąt jest równoległobokiem.
  • Każdy równoległobok jest prostokątem.
  • Każdy równoległobok, w którym przekątne są prostopadłe, jest kwadratem.
  • Każdy równoległobok, w którym wszystkie boki są równej długości, jest kwadratem.
  • Każdy równoległobok, który ma kąt prosty, jest prostokątem.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 13

Wytnij z papieru dowolny prostokąt. Narysuj w tym prostokącie odcinek łączący równoległe boki, nieprostopadły do tych boków. Rozetnij prostokąt wzdłuż narysowanego odcinka. Ułóż z otrzymanych części równoległobok niebędący prostokątem. Wklej go do zeszytu i zmierz jego wysokość.

Rn4MMvCC0XL2U
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Dany jest pewien prostokąt. Wyznaczono w tym prostokącie odcinek łączący równoległe boki, nieprostopadły do tych boków. Rozcięto prostokąt wzdłuż narysowanego odcinka. Ułożono z otrzymanych części równoległobok niebędący prostokątem. Czy wysokość równoległoboku jest równa wysokości prostokąta?

Ćwiczenie 14

Na których rysunkach nie zaznaczono poprawnie wysokości równoległoboku?

RtePb4AszZEOm1
Rysunek pięciu równoległoboków z poprowadzonymi dwoma wysokościami w każdym.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RGy39SDKCyRao
Zaznacz poprawne odpowiedzi. Możliwe odpowiedzi: 1. Rysunek B , 2. Rysunek D , 3. Rysunek A , 4. Rysunek C , 5. Rysunek E

  • Rysunek B
  • Rysunek D
  • Rysunek A
  • Rysunek C
  • Rysunek E
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RHwcgY3loEV2p
Ćwiczenie 14
Łączenie par. . Czy kwadrat jest równoległobokiem?. Możliwe odpowiedzi: Prawda, Fałsz. A. Możliwe odpowiedzi: Prawda, Fałsz
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 15

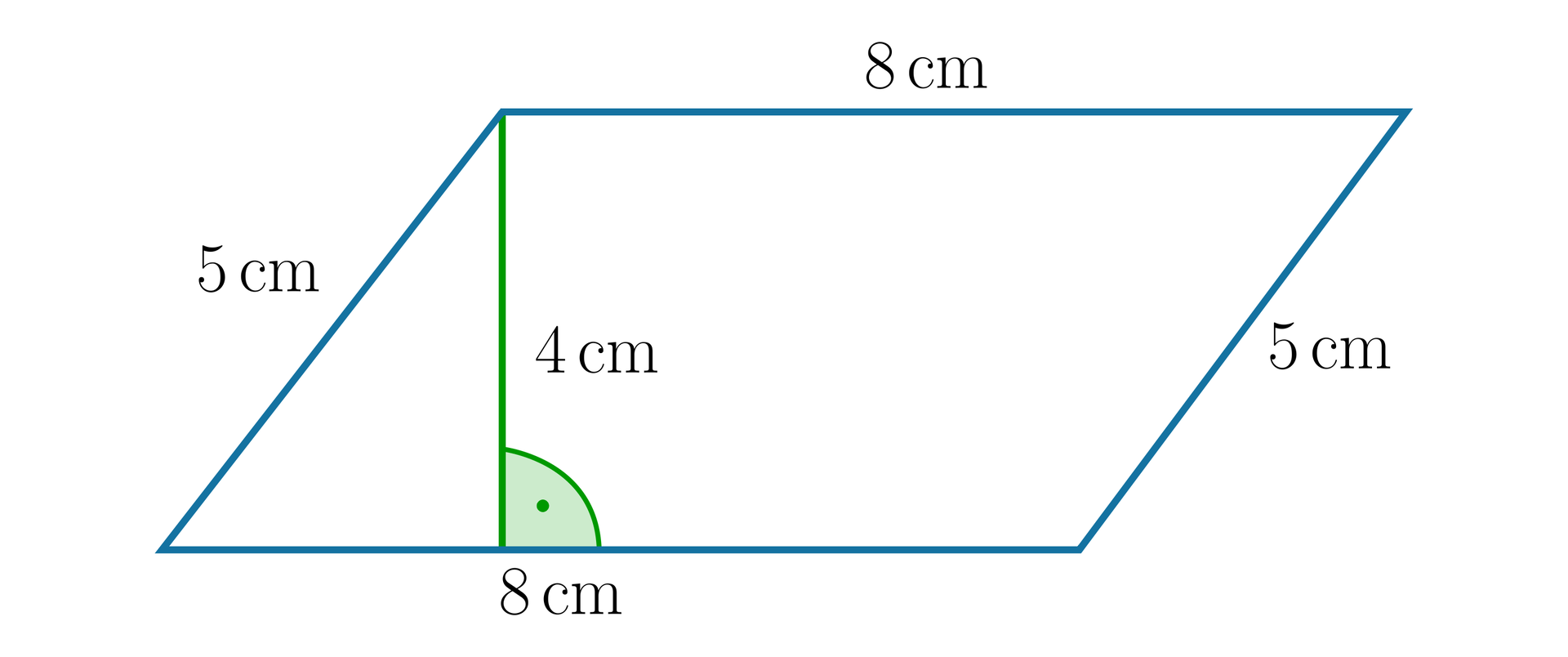
Podaj długość wysokości każdego z równoległoboków. Przyjmij, że długość jednej kratki to 1 cm.

Uwaga: Jeśli w równoległoboku nie da się odczytać wysokości z rysunku, przerysuj go do zeszytu i zmierz jego wysokość.

RHIx0ic7uRW6M1
Rysunki sześciu różnych równoległoboków.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1XNJRrLbHq5B
Ćwiczenie 15
Równoległobok, który jest kwadratem o boku długości 4 cm ma wysokość długości: Możliwe odpowiedzi: 1. h=4 cm, 2. h=2 cm, 3. h=8 cm
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 16

Rysunek przedstawia cztery równoległoboki.

RpKlnSDPPx7oi1
Rysunki czterech różnych równoległoboków.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wskaż zdanie prawdziwe.

R1RZDfHJeJVNL
Możliwe odpowiedzi: 1. Wszystkie równoległoboki mają jednakową wysokość., 2. Wśród równoległoboków na rysunku nie ma prostokątów., 3. Wszystkie równoległoboki mają jednakowe pola powierzchni., 4. Wśród równoległoboków nie ma kwadratu.

  • Wszystkie równoległoboki mają jednakową wysokość.
  • Wśród równoległoboków na rysunku nie ma prostokątów.
  • Wszystkie równoległoboki mają jednakowe pola powierzchni.
  • Wśród równoległoboków nie ma kwadratu.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R9ZGEN2iCJIqq
Ćwiczenie 16
Zaznacz wszystkie zdanie prawdziwe. Możliwe odpowiedzi: 1. Każdy prostokąt jest równoległobokiem., 2. Każdy równoległobok jest rombem., 3. Prostokąt o wymiarach 4 cm × 3 cm oraz kwadrat o boku długości 3 cm mają co najmniej jedną wysokość równej długości., 4.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 17

Narysuj równoległobok, który spełnia oba warunki:

Napisz instrukcję rysowania równoległoboku, który spełnia oba podane warunki:

  1. boki mają długości 8 cm i 5 cm,

  2. długość wysokości poprowadzonej do dłuższego boku jest równa 4 cm.

R1DfLGFoxFGgy
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1ZUKfhtuHboV
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
4. Własności prostokąta i kwadratu
6. Własności rombu