Pola wielokątów
7. Pola wielokątów - podsumowanie
Materiał zawiera ćwiczenia sprawdzające umiejętności w zakresie obliczania pól wielokątów. Potrzebne wzory znajdziesz w mapie myśli, zamieszczonej na początku materiału.
Rozwiązując ćwiczenia, będziesz wyznaczać pola wielokątów oraz elementy tych wielokątów (np. wysokości, długości boków).
Test końcowy, pomoże Ci określić stopień ukształtowanych umiejętności dotyczących określania własności figur geometrycznych na płaszczyźnie.
gdzie oznacza podstawę trójkąta oraz wysokość trójkąta, 2. Pole rombu ,
gdzie oznacza podstawę rombu oraz wysokość rombu,,
gdzie , są przekątnymi rombu. , 3. Pole prostokąta ,
gdzie , oznaczają długości boków prostokąta. , 4. Pole równoległoboku ,
gdzie oznacza długość podstawy równoległoboku, a oznacza wysokość równoległoboku. , 5. Pole kwadratu ,
gdzie oznacza długość boku kwadratu , 6. Pole trapezu
gdzie oznaczają długości podstaw trapezu, a wysokość trapezu
Zapoznaj się z informacjami dotyczącymi wyznaczania pola wielokątów.
Pole trójkąta
,
gdzie oznacza podstawę trójkąta oraz wysokość trójkąta.Obok informacji znajduje się ilustracja przedstawiająca trójkąt z zaznaczoną wysokością o długości prostopadłą do podstawy o długości .
Pole rombu
,
gdzie oznacza podstawę rombu oraz wysokość rombu,,
gdzie , są przekątnymi rombu.
Obok informacji znajduje się ilustracja przedstawiająca romb z zaznaczoną wysokością o długości prostopadłą do podstawy o długości . Poza tym na rysunku znajdują się dwie przekątne o długościach i .
Pole prostokąta
,
gdzie , oznaczają długości boków prostokąta.Obok informacji znajduje się ilustracja przedstawiająca prostokąt o szerokości i długości .
Pole równoległoboku
,
gdzie oznacza długość podstawy równoległoboku, a oznacza wysokość równoległoboku.Obok informacji znajduje się ilustracja przedstawiająca równoległobok z zaznaczoną wysokością o długości prostopadłą do podstawy o długości .
Pole kwadratu
,
gdzie oznacza długość boku kwadratu.Obok informacji znajduje się ilustracja przedstawiająca kwadrat o krawędzi .
Pole trapezu
gdzie oznaczają długości podstaw trapezu, a wysokość trapezu.Obok informacji znajduje się ilustracja przedstawiająca trapez z zaznaczoną wysokością o długości prostopadłą do obu podstaw. Krótsza podstawa ma długość , a dłuższa .
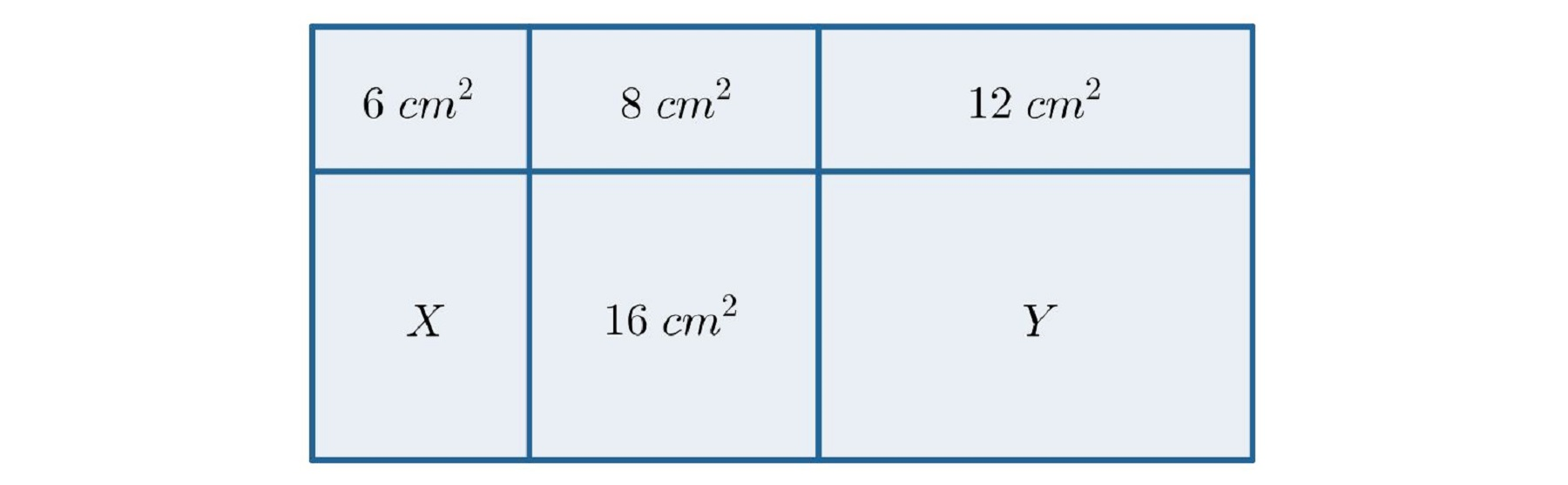
Figura przedstawiona na rysunku składa się z prostokątów. Długości boków każdego z tych prostokątów wyrażają się liczbami naturalnymi. W każdym z prostokątów wpisane jest jego pole. Oblicz pola oznaczone literami oraz .
Na którym rysunku odcinek w zielonym kolorze nie jest wysokością równoległoboku?

Na którym rysunku przedstawiono dwie wysokości równoległoboku?

W równoległoboku dane są długości jednego boku oraz dwóch wysokości.

Krótszy bok równoległoboku ma długość , a wysokość na niego prowadzona . Wysokość poprowadzona na krótszy bok ma długość .
Oblicz pola trapezów przedstawionych na rysunku.

Oblicz pole trapezu, którego:
krótsza i dłuższa podstawa mają odpowiednio długość i oraz wysokość jest równa
jedna podstawa ma długość , druga jest o dłuższa, a wysokość jest średnią arytmetyczną długości dwóch podstaw.
Rysunek przedstawia trójkąt prostokątny.

Oblicz pole trójkąta przedstawionego na rysunku poniżej. Podaj wynik w postaci liczby dziesiętnej zaokrąglonej do trzech miejsc po przecinku.

W trójkącie dane są długości dwóch wysokości oraz długość boku .

Na rysunku znajdują się: trójkąt różnoboczny , trójkąt prostokątny oraz trójkąt równoramienny .

Prostokąt podzielono na trzy figury, jak na rysunku poniżej.

Na terenie w kształcie wielokąta przedstawionego na rysunku postanowiono posiać trawę.

Trapez o polu podzielono na dwa trójkąty, tak jak na rysunku. Oblicz pole każdego z trójkątów. Wpisz otrzymaną liczbę w puste pola.
Trapez o polu oraz długości podstaw i podzielono na dwa trójkąty, prowadząc przekątną .
Pole trójkąta wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. .
Wysokość trapezu wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. .
Długości podstaw wszystkich figur na rysunku są takie same i są równe . Oblicz sumę pól wszystkich czterech figur. Wynik wpisz w puste luki.

Suma pól wszystkich czterech figur wynosi Tu uzupełnij .
O ile centymetrów kwadratowych pole drugiego kwadratu jest większe niż pierwszego?
Odpowiedź: O 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. .
Ile razy pole drugiego kwadratu jest większe od pierwszego?
Odpowiedź: 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. razy.
Jaką częścią pola drugiego kwadratu jest pole pierwszego kwadratu?
Odpowiedź: 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. .
Oblicz pole figury przedstawionej na rysunku, jeżeli pole jednej kwadratowej kratki jest równe .

Przeciągnij i upuść w wyznaczone miejsce odpowiedni wynik. Obwód tego prostokąta jest równy 1. , 2. , 3. , 4. .
Jakie czworokąty przedstawiono na rysunku poniżej? Jakie są ich pola? Przyjmij, że jedna kratka to jedna jednostka.
Jakiej wielkości są pola czworokątów przedstawionych na rysunku poniżej? Przyjmij, że jedna kratka to jedna jednostka.

Na rysunku proste i są równoległe i oddalone od siebie o .

- Pola trójkątów i są równe.
- Suma pól trójkątów i jest równa sumie pól trójkątów i .
- Pole trójkąta jest razy większe niż pole trójkąta .
- Pole trójkąta jest o większe od sumy pól pozostałych trójkątów.
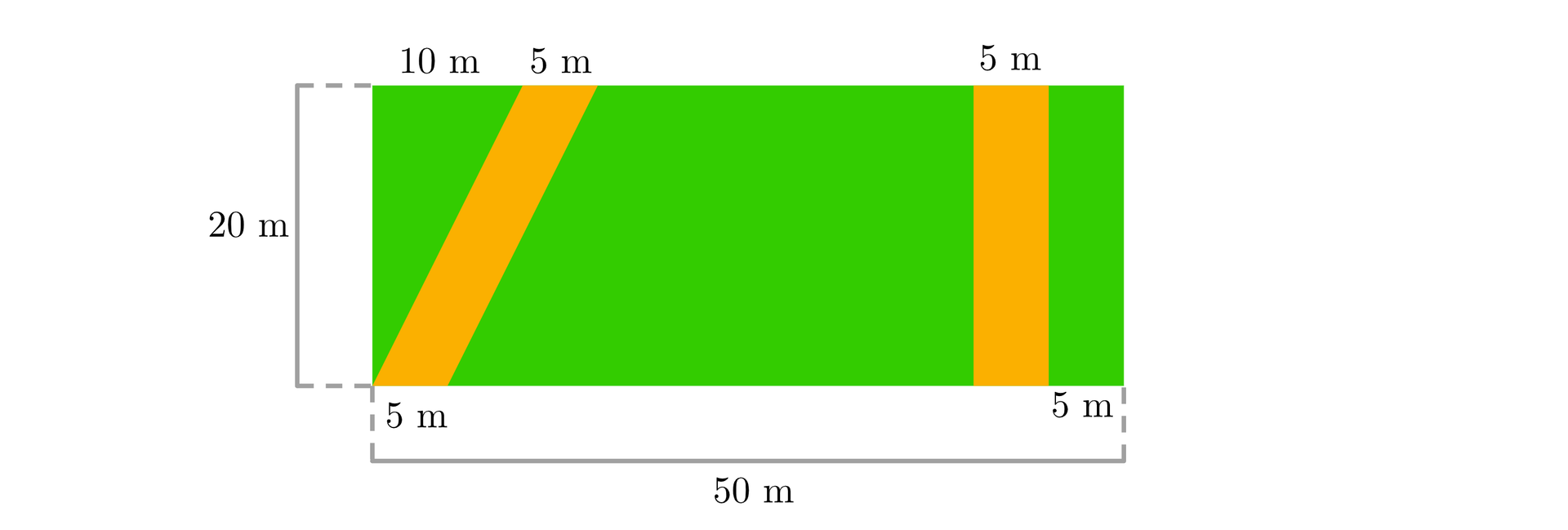
Trawnik na osiedlu, na którym mieszka Bartek, ma kształt prostokąta o wymiarach i . Przez trawnik biegną dwie alejki o kształcie i wymiarach podanych na rysunku.
Uzupełnij poniższą lukę. Kliknij w nią, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. Odpowiedź: Rzeczywista odległość między tymi miejscowościami wynosi 1. , 2. , 3. , 4. , 5. .
Uzupełnij lukę w zdaniu, wpisując poprawną wartość. Odpowiedź: Długość ulicy na planie w skali wynosi Tu uzupełnij .
Uzupełnij.
Pole kwadratu o boku długości wynosi ............ , czyli ............. Jeżeli pole o powierzchni podzielimy na trzy działki o jednakowej powierzchni, to pole jednej działki będzie równe ............ .
b) 1. , 2. , 3. , 4. , 5. , 6.
c) 1. , 2. , 3. , 4. , 5. , 6.
Przeciągnij i upuść.
, , , , ,
a) ................
b) ................
c) ................
Test z własności figur geometrycznych na płaszczyźnie
Własności figur geometrycznych na płaszczyźnie
Jeżeli litery i oznaczają długości przekątnych czworokąta, to stosując wzór możemy obliczyć pole Możliwe odpowiedzi: 1. równoległoboku, 2. rombu, 3. prostokąta, 4. kwadratu
- równoległoboku
- rombu
- prostokąta
- kwadratu
Jeżeli - podstawa czworokąta, a - wysokość prostopadła do tej podstawy, to stosując wzór nie możemy obliczyć pola dowolnego Możliwe odpowiedzi: 1. równoległoboku, 2. rombu, 3. prostokąta, 4. trapezu
- równoległoboku
- rombu
- prostokąta
- trapezu
Rysunek przedstawia trapez i obliczenie jego pola. Możesz zmieniać położenie wierzchołków tego trapezu, ale długość wysokości cały czas będzie taka sama.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1DDUFDtS
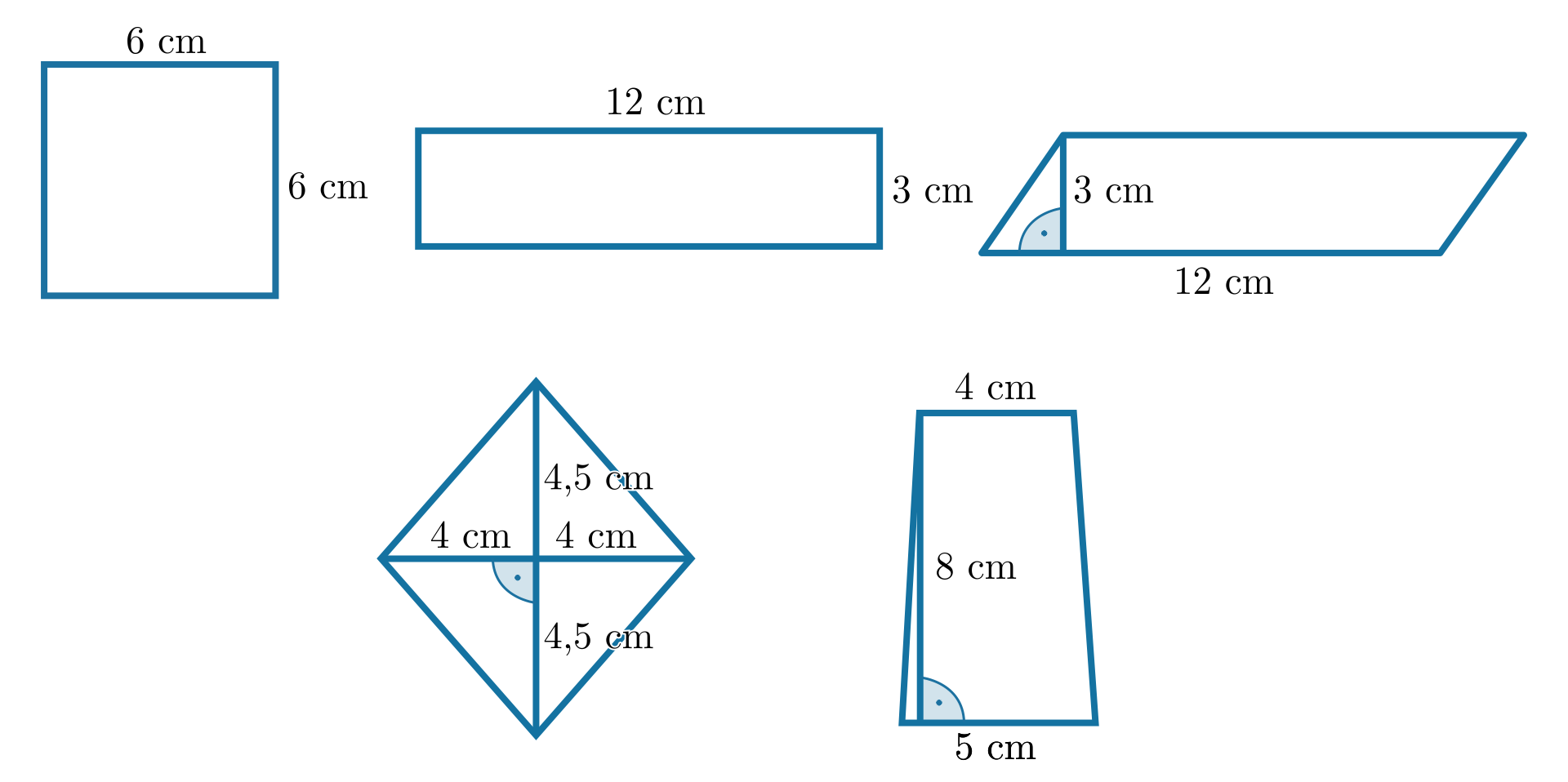
Oblicz pola figur przedstawionych na rysunku.


Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1DDUFDtS

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1DDUFDtS

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1DDUFDtS

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1DDUFDtS

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1DDUFDtS
Narysuj: kwadrat, prostokąt, równoległobok, romb i trapez tak, aby każda z figur miała pole równe .
Sprawdź poprawność wykonania rysunków, budując takie same figury z dynamiczną kartą pracy.
Ustaw wierzchołki tak, by otrzymać kolejne figury o takich samych wymiarach, jak w zeszycie.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1DDUFDtS
Ścianę o wymiarach 4,5 m i 2,5 m trzeba wyłożyć glazurą. Wskaż zdania prawdziwe.
- Na wyłożenie tej ściany glazurą potrzeba kwadratowych płytek o boku .
- Na wyłożenie tej ściany glazurą potrzeba kwadratowych płytek o boku .
Rolnik podzielił pole o powierzchni 2,5 ha na 25 jednakowych działek. Wskaż zdania prawdziwe.
- Jedna działka ma powierzchnię .
- Każda działka ma powierzchnię arów.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.