Działania pamięciowe na liczbach naturalnych
11. Pamięciowe działania na liczbach naturalnych - podsumowanie
Dlaczego warto nauczyć się wykonywania rachunków bez pomocy kalkulatora, kartki i długopisu? Dlatego, że na przykład leżąc na plaży nie mamy tych przedmiotów pod ręką, a musimy wykonać potrzebne obliczenia. Dodawanie, odejmowanie, mnożenie i dzielenie pamięciowe pobudza logiczne myślenie i ćwiczy pamięć!

Wykonując ćwiczenia zawarte w tym materiale, będziesz mieć okazję sprawdzić swoje umiejętności wykonywania działań pamięciowych na liczbach naturalnych, w tym szacowania wyników i działań na dużych liczbach.
Na start
Liczby naturalne to , , , , , , , , , , . Najmniejszą liczbą naturalną jest . Największej liczby nie ma, zawsze można podać liczbę większą od danej.
Liczby naturalne zapisujemy za pomocą dziesięciu cyfr: , , , , , , , , , w systemie dziesiątkowym pozycyjnym.
System jest pozycyjny, bo znaczenie cyfry w liczbie zależy od pozycji, jaką w tej liczbie zajmuje. Pozwala to na zapisanie i odczytanie dowolnej liczby, np.: „sześć milionów siedemset sześćdziesiąt dziewięć tysięcy dwieście osiemdziesiąt pięć.”
Nasz system liczenia jest również dziesiątkowy, bo jednostek niższego rzędu to jednostka rzędu wyższego (np. jedności to jedna dziesiątka, dziesiątek to jedna setka, setek to jeden tysiąc).
Liczby naturalne możemy dodawać, odejmować, mnożyć i dzielić. Liczby, które dodajemy, odejmujemy, mnożymy lub dzielimy mają swoje nazwy.

Czy wśród uczestników pikniku znalazł się ktoś, kto zjadł więcej niż jedną kiełbaskę? 1. tak, 2. , 3. , 4. , 5. , 6. , 7. nie, 8. , 9.
Dodajemy i odejmujemy w pamięci
Przeciągnij i upuść.
, , , , ,
a) ............ b) ............ c) ............
d) ............ e) ............ f) ............
- ,
- ,
- ,
- .
Wskaż prawidłową odpowiedź. Możliwe odpowiedzi: 1. Ponieważ ., 2. Ponieważ suma liczby parzystej i nieparzystej jest liczbą nieparzystą., 3. Dlatego, że jeżeli jeden składnik sumy zwiększymy, a drugi zmniejszymy o tyle samo, to wynik dodawania się nie zmieni., 4. Ponieważ suma liczby zakończonej cyfrą i liczby zakończonej cyfrą musi kończyć się cyfrą .
- Ponieważ
- Ponieważ suma liczby parzystej i nieparzystej jest liczbą nieparzystą.
- Dlatego, że jeżeli jeden składnik sumy zwiększymy, a drugi zmniejszymy o tyle samo, to wynik dodawania się nie zmieni.
- Ponieważ suma liczby zakończonej cyfrą i liczby zakończonej cyfrą musi kończyć się cyfrą .
- ,
- ,
- ,
- ,
- .
Wskaż prawidłową odpowiedź. Możliwe odpowiedzi: 1. Dlatego, że jeśli od liczby zakończonej cyfrą odejmujemy liczbę zakończoną cyfrą , to wynik musi się kończyć cyfrą ., 2. Ponieważ różnica liczby parzystej i nieparzystej jest liczbą nieparzystą., 3. Ponieważ ., 4. Ponieważ, jeżeli dwie liczby zmniejszymy lub zwiększymy o tyle samo, to różnica tych liczb nie zmieni się.
- Dlatego, że jeśli od liczby zakończonej cyfrą odejmujemy liczbę zakończoną cyfrą , to wynik musi się kończyć cyfrą .
- Ponieważ różnica liczby parzystej i nieparzystej jest liczbą nieparzystą.
- Ponieważ
- Ponieważ, jeżeli dwie liczby zmniejszymy lub zwiększymy o tyle samo, to różnica tych liczb nie zmieni się.
Przeciągnij i upuść.
, , , , ,
a) ............ b) ............ c) ............
d) ............ e) ............ f) ............
- Basia zapłaciła za soki złotych. Podała pani w kasie i otrzymała złote reszty.
- Krzyś, dodając liczby i do liczby , dodał i od wyniku odjął .
- Tomek oddał pożyczki, którą zaciągnął u Bartka. Oddał mu , a Bartek dał mu .
- Mama Jadzi i Dorotki dała córkom na klasową wycieczkę do ogrodu zoologicznego. Każdy uczeń miał wpłacić wychowawczyni po złote. Dziewczęta podzieliły się równo resztą pieniędzy. Każda wzięła sobie po złote.
Mnożymy i dzielimy w pamięci
Przeciągnij i upuść.
, , , , ,
a) ............ b) ............ c) ............
d) ............ e) ............ f) ............
Uzupełnij.
a) ............ b) ............ c) ............ d) ............
e) ............ f) ............ g) ............ h) ............
Oblicz w pamięci, a następnie przeciągnij i upuść.
, , , , , , , , ,
a) ............ b) ............ c) ............ d) ............
e) ............ f) ............ g) ............ h) ............
Przeciągnij i upuść.
, , , , , , , ,
a) ............ b) ............ c) ............
d) ............ e) ............ f) ............
g) ............ h) ............ i) ............
Jeżeli jeden z czynników zmniejszymy pewną liczbę razy, a drugi zwiększymy tyle samo razy, to wynik mnożenia się nie zmieni.
Jeżeli każdą z dwóch liczb ilorazu zmniejszymy lub zwiększymy tyle samo razy, to wynik dzielenia się nie zmieni.
Odpowiedź: Tata ma Tu uzupełnij lat.Ile lat mają razem Karol i jego rodzice?
Odpowiedź: Karol i jego rodzice mają razem Tu uzupełnij lat.
Rozwiąż zadanie i zapisz odpowiedź.
Postaraj się zapisać treść zadania za pomocą jednego wyrażenia, a następnie obliczyć jego wartość.
Marek ma płyt. Ile będzie miał płyt, jeśli dokupi razy więcej niż ma?
Państwo Kowalscy kupili telewizor za i odtwarzacz o droższy od telewizora. Ile zapłacili razem za telewizor i odtwarzacz?
Uczniowie na zielonej szkole nocowali w hotelu. Zajęli pokoi –osobowych, pokoje –osobowe, pokoi –osobowych i jeden pokój –osobowy. Ilu uczniów pojechało na zieloną szkołę?
Do dwóch szkół uczęszcza uczniów. W pierwszej szkole jest uczniów. O ilu uczniów więcej uczęszcza do drugiej szkoły?
W teatrze na parterze znajduje się rzędów po miejsca w każdym, a na balkonie rzędów po miejsc w każdym. Ile miejsc jest w teatrze?
Uzupełnij.
a) ............
b) ............
c) ............
d) ............
e) ............
f) ............
g) ............
h) ............
Uzupełnij cyframi.
a) ............ ............ ............
b) ............ ............ ............
c) ............ ............ ............ ............
d) ............ ............
Szacowanie wyników
Jak sobie poradzić bez kalkulatora, kartki i długopisu, gdy nasze umiejętności rachunkowe nie pozwalają nam szybko i sprawnie liczyć? Kiedy nie ma czasu na żmudne dodawanie, odejmowanie, mnożenie lub dzielenie, to wykonujemy szacowanie. Zadowalamy się wtedy wynikiem przybliżonym.
Film dostępny pod adresem /preview/resource/RdBTONStzz9Lj
Animacja pokazująca przykłady szacowania wyników.
Nie wykonując dokładnych obliczeń, połącz w pary.
1 917 + 4 821, 2 344 + 2 314, 3 456 + 2 452, 2 333 + 2 645
| 5 908 | |
| 4 658 | |
| 6 738 | |
| 4 978 |
Na rysunku przedstawiony jest fragment planu.

Odpowiedź: Odległość jaką należy pokonać wynosi Tu uzupełnij .O ile kilometrów dłuższa jest droga z Janowa do Adamowa, gdy jedzie się przez Danielów od trasy przez Julianów?
Odpowiedź: Droga ta jest dłuższa o Tu uzupełnij .
Poniżej przedstawiono cennik biletów do muzeum.
Muzeum matematyczne | |
|---|---|
bilet normalny | |
bilet ulgowy (dzieci, studenci, emeryci) | |
opłata przewodnika | |
Odpowiedź: Zapłacili Tu uzupełnij.Dwie rodziny pięcioosobowe (rodzice i troje dzieci) wynajęli wspólnie jednego przewodnika. Ile zapłacili razem za bilety i przewodnika?
Odpowiedź: Zapłacili Tu uzupełnij.
Pomiędzy czwórki wstaw znaki działań lub nawiasy tak, aby otrzymać wskazany wynik.
Działania na dużych liczbach
W naszym otoczeniu często spotykamy duże liczby. Ceny niektórych produktów zapisane są za pomocą liczb wielocyfrowych – rower kosztuje ponad , a komputer około . Podróżując, pokonujemy duże odległości. Z Warszawy do Paryża jest , a do Nowego Jorku . Dzięki umiejętności liczenia na dużych liczbach wiemy, że komputer jest droższy od roweru razy, a Paryż jest o bliżej Warszawy niż Nowy Jork.
Do rachunków na takich liczbach nie zawsze potrzebujemy kalkulatora, niektóre można wykonać w pamięci. Jeśli umiemy dodawać, odejmować, mnożyć i dzielić pamięciowo małe liczby, to powinniśmy poradzić sobie także z działaniami na niektórych większych liczbach.

Film dostępny pod adresem /preview/resource/RJO98WsMXT3OJ
Animacja przedstawia przykłady pamięciowego dodawania liczb zakończonych zerami.
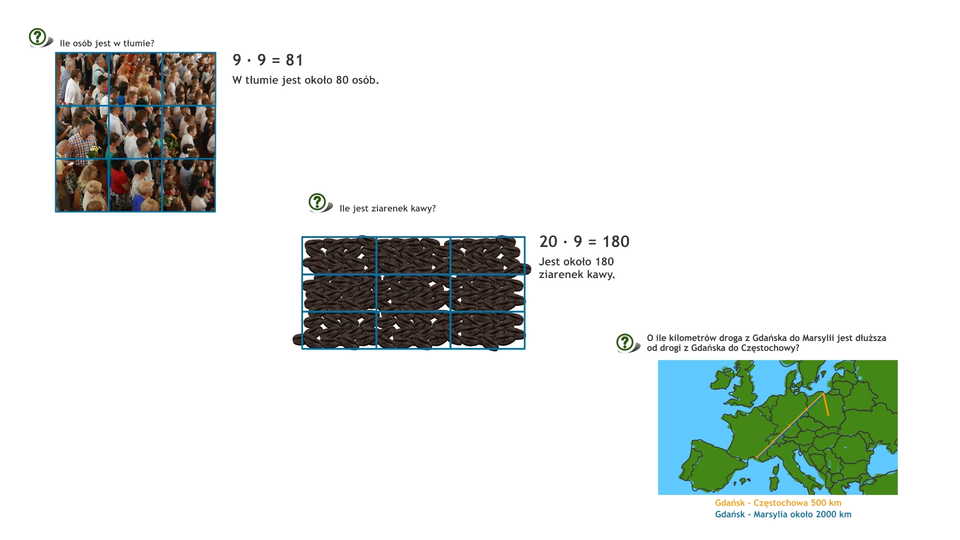
Jeśli wiemy, że , to dodawanie liczb i sprowadza się do dodania i oraz dopisania do wyniku, czyli , zera.
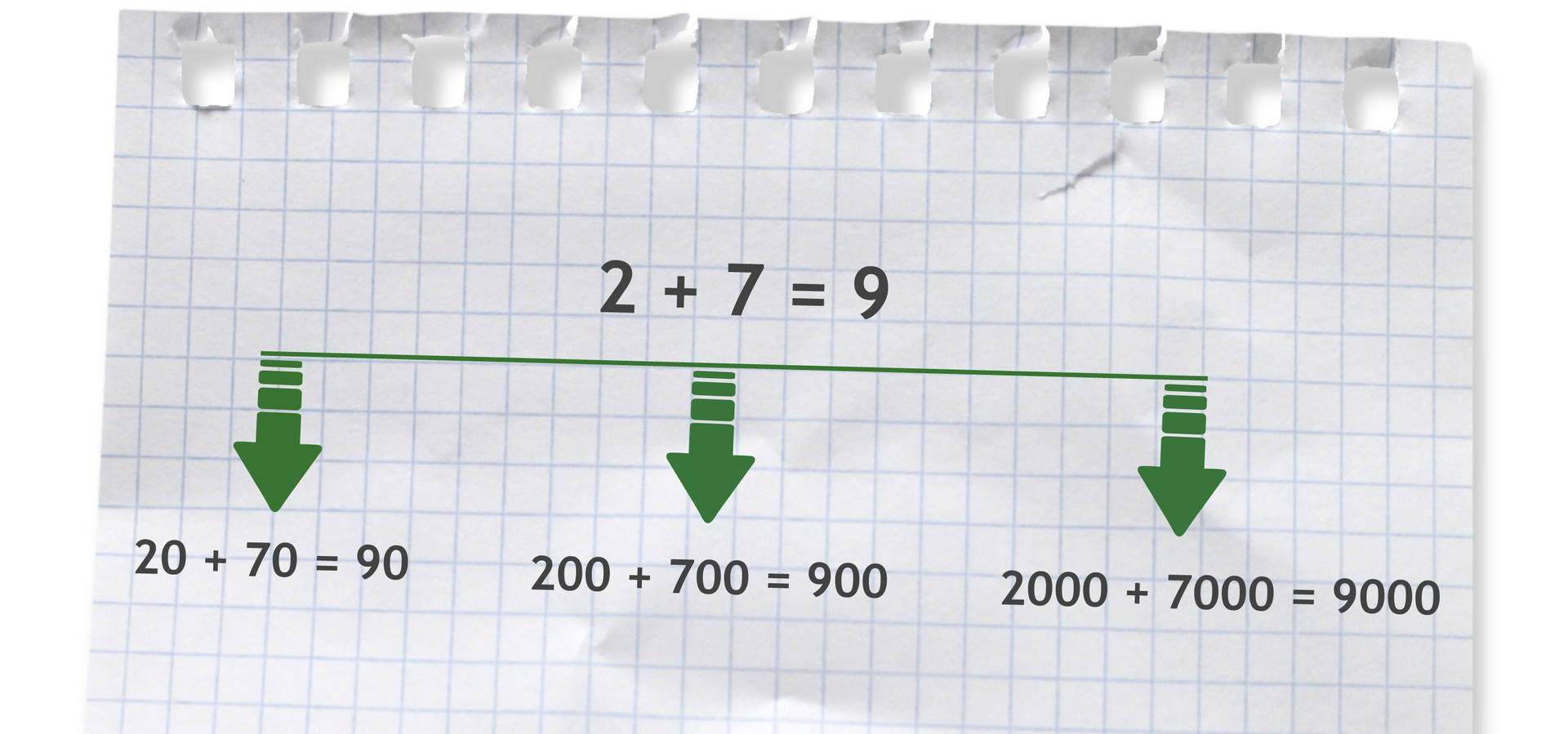
Analogicznie dodajemy i . Znów dodajemy i i dopisujemy do wyniku, czyli , dwa zera. Dodając i postępujemy tak samo. Dodajemy i , a do wyniku dopisujemy trzy zera.
Większe liczby dodajemy podobnie.
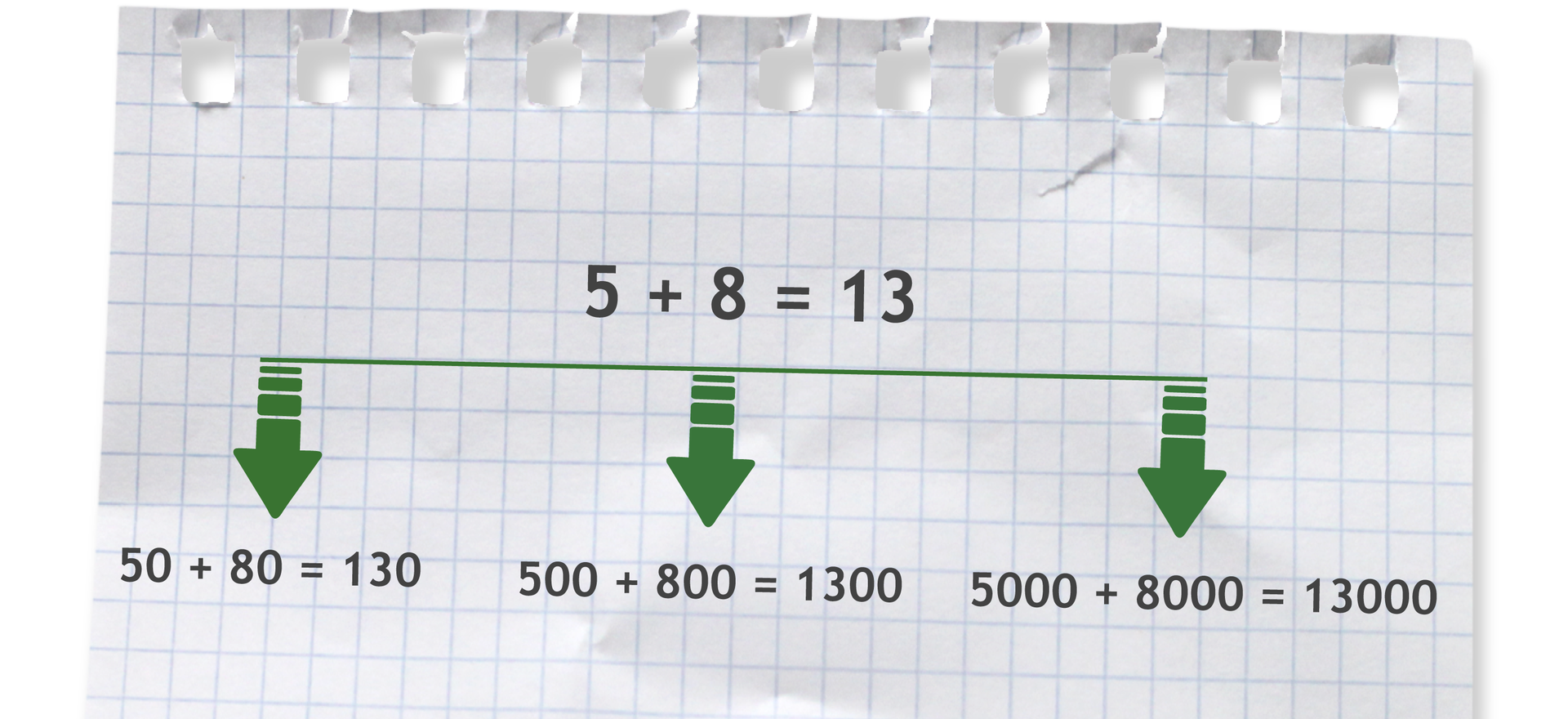
Znając wynik dodawania liczb 35 i 7, łatwo można ustalić wyniki działań: 350 + 70, 3500 + 700, itd.


Film dostępny pod adresem /preview/resource/RqyLusAN19XJu
Animacja przedstawia przykłady pamięciowego odejmowania liczb zakończonych zerami.
Znając wynik działania 38 - 12, łatwo można ustalić wyniki działań: 3800 - 1200, 380000- 120000,itd.

Uzupełnij.
a) ............
b) ............
c) ............
d) ............
e) ............
f) ............
g) ............
h) ............
i) ............
j) ............
Niektóre z podanych liczb są wynikami poniższych działań. Odpowiednio przeciągnij i upuść.
, , , , , , , , , , , , , , ,
..................
..................
..................
..................
..................
..................
..................
..................
Wiadomo, że:
Zastanów się, jakich liczb dotyczy ta zależność. Czy wszystkich? A może składniki sum coś łączy? Podaj kilka kolejnych przykładów.
Jeśli potrafimy mnożyć w pamięci liczby w zakresie , to poradzimy sobie również z mnożeniem niektórych dużych liczb.
Najłatwiej mnożyć liczby przez , , , itd.
Aby pomnożyć liczbę przez , wystarczy do tej liczby dopisać na jej końcu jedno zero.
Aby pomnożyć liczbę przez , wystarczy do tej liczby dopisać na jej końcu dwa zera.
Aby pomnożyć liczbę przez , wystarczy do tej liczby dopisać na jej końcu trzy zera.
Aby pomnożyć liczbę przez , wystarczy do tej liczby dopisać na jej końcu cztery zera.
Jak pomnożyć daną liczbę przez , , , , lub przez , , , , ? Czy jest to równie proste?

Film dostępny pod adresem /preview/resource/R1ObVTcbuRSeP
Animacja przedstawia przykład pamięciowego mnożenia liczb zakończonych zerami.

Film dostępny pod adresem /preview/resource/R1ZZO1C86Who9
Animacja przedstawia przykłady pamięciowego mnożenia liczb zakończonych zerami.
Jeśli mnożymy liczby, które są zakończone zerami, to:
mnożymy liczby, które zostaną po odrzuceniu zer,
do otrzymanego wyniku dopisujemy tyle zer, ile łącznie odrzuciliśmy.
Dzielenie i mnożenie są działaniami wzajemnie odwrotnymi.
, zatem
, zatem
, zatem
, zatem
Porównaj zapis dzielnej i ilorazu. Czym różnią się zapisy tych liczb?
Jeżeli dzielimy przez liczbę zakończoną zerem (lub zerami), to jako wynik zapisujemy dzielną bez jednego zera na końcu.
Dzielenie przez możemy zastąpić dwukrotnym dzieleniem przez .
, czyli
, czyli
, czyli
Porównaj zapis dzielnej i ilorazu. Czym teraz różnią się zapisy tych liczb?
Jeżeli dzielimy przez liczbę zakończoną zerami, to jako wynik zapisujemy dzielną z opuszczonymi na końcu dwoma zerami.
Podobnie zapisujemy wynik dzielenia przez , , , Wynikiem jest odpowiednio dzielna bez trzech, czterech, pięciu, zer na końcu.

Film dostępny pod adresem /preview/resource/R1RlNhbxCL5Zq
Animacja przedstawia przykłady pamięciowego dzielenia liczb zakończonych zerami.
Przyjrzyj się poniższym przykładom, w których pokazano, jak można ułatwić dzielenie, gdy w dzielnej i dzielniku jest inna liczba zer.
Uzupełnij.
a) ............
b) ............
c) ............
d) ............
e) ............
f) ............
g) ............
h) ............
Uzupełnij.
a) 2800 : 400 = ............
b) 480 : 60 = ............
c) 2600 : 200 = ............
d) 81000 : 9000 = ............
e) 3000 : 500 = ............
f) ............ : 300 = 5
g) ............ : 70 = 60
h) 35000 : ............ = 50
Nie wykonując obliczeń, uzupełnij znakiem: >, < lub =.
a) 1100 + 2600 ............ 990 + 2600
b) 90000 + 20000 ............ 1000000
c) 8400 – 2500 ............ 8400 – 2400
d) 10000 – 1 ............ 999 + 999
e) 360 : 40 ............ 3600 : 400
f) 50∙600 ............ 3000
Uzupełnij zdania, wpisując w luki odpowiednie kwoty. W poniedziałek otrzymał banknotów po , czyli Tu uzupełnij.We wtorek otrzymał banknotów po , czyli Tu uzupełnij.W czwartek otrzymał banknotów po , czyli Tu uzupełnij.W piątek otrzymał banknotów po , czyli Tu uzupełnij.W sobotę pan Kowalski obliczył, że w ciągu tego tygodnia wypłacił razem Tu uzupełnij.
Pan Kowalski kilka razy w tygodniu wypłacał pieniądze z banku.
Uzupełnij.
W poniedziałek otrzymał 10 banknotów po 100 zł , czyli ............ zł.
We wtorek otrzymał 100 banknotów po 50 zł, czyli ............ zł.
W czwartek otrzymał 350 banknotów po 10 zł, czyli ............ zł.
W piątek otrzymał 30 banknotów po 200 zł, czyli ............ zł.
W sobotę pan Kowalski obliczył, że w ciągu tego tygodnia wypłacił razem ............ zł.
Pani Jola, mieszkanka Warszawy, postanowiła zwiedzić kilka innych stolic. Najpierw poleciała do Tokio, a stamtąd do Pekinu. Przed powrotem do Warszawy zwiedziła jeszcze Kair. W informacji turystycznej dowiedziała się, że z Warszawy do Tokio jest 8 600 km, z Tokio do Pekinu – 2 100 km, z Pekinu do Kairu – 7 500 km, a z Kairu do Warszawy – 2 600 km. Jaką łączną długość miała trasa, którą pokonała pani Jola podczas tej wycieczki?
............ km
Łatwo możemy pomnożyć w pamięci dwie liczby dwucyfrowe trochę mniejsze od , na przykład i .
Aby wykonać takie działanie, musimy najpierw znaleźć liczby, które są dopełnieniami czynników do , czyli w przypadku jest to
(tyle brakuje do ), a w przypadku jest to (tyle brakuje do ).
Mamy następującą sytuację:
Zaczynamy zapisywać wynik tego mnożenia.
Na początku odejmujemy od dowolnego czynnika liczbę, która jest dopełnieniem drugiego czynnika. Otrzymujemy liczbę ( lub ), która jest początkiem wyniku mnożenia.
Następnie do tej liczby dopisujemy iloczyn liczb, które są dopełnieniami, czyli . Gdy iloczyn dopełnień jest liczbą jednocyfrową, poprzedzamy go cyfrą .
W ten sposób można wprawdzie mnożyć dowolne liczby dwucyfrowe, ale gdy są one znacznie mniejsze niż , to rachunki pamięciowe są uciążliwe.
Spróbuj pomnożyć w ten sposób inne liczby.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.