Działania pamięciowe na liczbach naturalnych
7. Pamięciowe dzielenie liczb naturalnych
Analizując przykłady zawarte w tym materiale dowiesz się, jak dzielić liczby naturalne bez reszty i z resztą.
Dzielenie bez reszty
Kasia ma cukierków i chce się nimi po równo podzielić z dwiema koleżankami. Ile cukierków powinna dostać każda z dziewcząt?

Film dostępny pod adresem /preview/resource/RqhaBQnItVIXy
Animacja przedstawia zadanie tekstowe, które należy rozwiązać korzystając z pamięciowego dzielenia liczb naturalnych.
Odpowiedź: Każda z dziewcząt powinna dostać cukierków.
Liczby występujące w dzieleniu mają swoje nazwy.

Rysunek przedstawia bukiet złożony z pięciu róż. Ile takich bukietów można ułożyć ze róż?

Film dostępny pod adresem /preview/resource/RFAIN9SBsDsVv
Animacja przedstawia zadanie tekstowe, które rozwiązano korzystając z pamięciowego dzielenia liczb naturalnych.
Odpowiedź: Ze róż można ułożyć bukietów po róż w każdym bukiecie.
Mnożenie i dzielenie to działania wzajemnie odwrotne.
Poprawność dzielenia można sprawdzić za pomocą mnożenia.
RoY2KiJwbIYCZ1 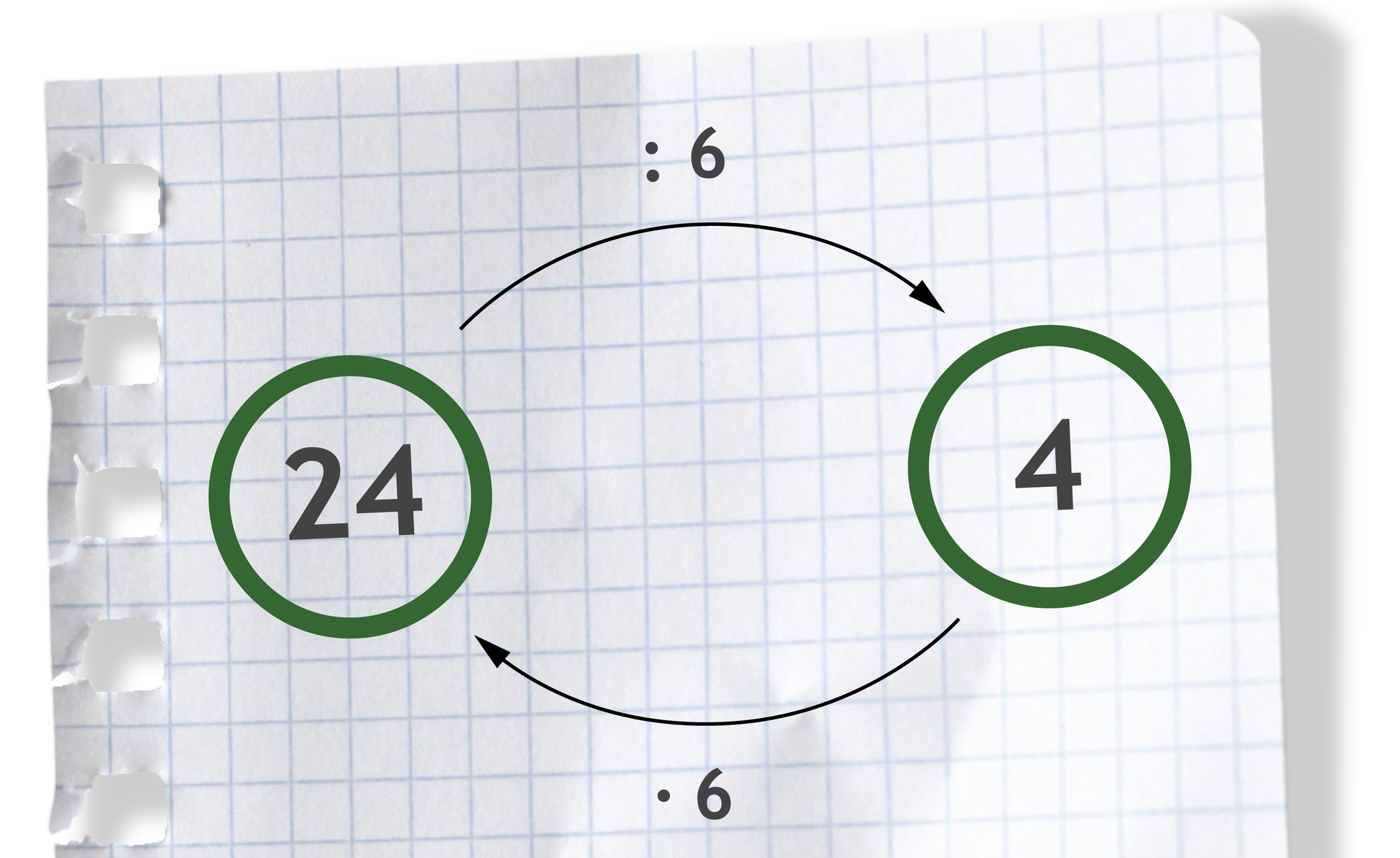 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
, bo .
Spójrz, jak różne osoby w klasie poradziły sobie z dzieleniem .
. osoba | . osoba | . osoba |
Czy wiesz, w jaki sposób osoby wykonywały obliczenia?
W bloku, w którym mieszka Kamil, część okien zasłania olbrzymie drzewo. Wiemy, że cały blok posiada okien i ma pięter. Ile okien znajduje się na każdym piętrze tego budynku (na parterze nie ma okien)?
W pamięciowym wykonywaniu dzielenia bardzo pomaga znajomość tabliczki mnożenia.
Iloraz liczb i
Odpowiedź: Tu uzupełnij Iloraz liczb i
Odpowiedź: Tu uzupełnij Iloraz liczb i
Odpowiedź: Tu uzupełnij Iloraz liczb i
Odpowiedź: Tu uzupełnij Iloraz liczb i
Odpowiedź: Tu uzupełnij
Odpowiedz na poniższe pytania i uzupełnij luki o szukane liczby. Ile banknotów dwudziestozłotowych otrzymał?
Odpowiedź: Powinien otrzymać Tu uzupełnij banknoty dwudziestozłotowe.Ile banknotów dziesięciozłotowych otrzymał?
Odpowiedź: Powinien otrzymać Tu uzupełnij banknotów dziesięciozłotowych.
Odpowiedz na poniższe pytania i uzupełnij luki o szukane liczby. Ile monet pięciozłotowych otrzymała?
Odpowiedź: Ania otrzymała Tu uzupełnij monet pięciozłotowych.Ile monet dwuzłotowych otrzymała?
Odpowiedź: Ania otrzymała Tu uzupełnij monet dwuzłotowych.
Dowód:
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. , bo 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. , bo 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. Jeżeli dzielna jest równa dzielnikowi (różnej od zera), to iloraz jest równy 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. .
Dowód:
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. , bo 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. , bo 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. Jeżeli dzielnik jest równy jeden, to iloraz jest równy 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. .
Dowód:
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. , bo 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36. , bo 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. dzielnej, 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. , 26. , 27. , 28. , 29. , 30. dzielnikowi, 31. , 32. , 33. , 34. , 35. , 36.
- tygodni
- tygodnie
- tygodnie
- tygodnie
- Tu uzupełnij
- Tu uzupełnij
- Tu uzupełnij
- Tu uzupełnij
- Tu uzupełnij
- Tu uzupełnij
- Tu uzupełnij
- Tu uzupełnij
- Tu uzupełnij
- Tu uzupełnij
- Tu uzupełnij
- Tu uzupełnij
- Tu uzupełnij
- Tu uzupełnij
- Tu uzupełnij
Dzielenie z resztą
Basia stwierdziła, że liczby nie można podzielić przez . Zosia się z nią nie zgodziła i twierdzi, że można. Kto ma rację Basia czy Zosia? A może obie mają rację? Przekonajmy się.
Argumenty Basi
Film dostępny pod adresem /preview/resource/R1HaiU8B9HFpa
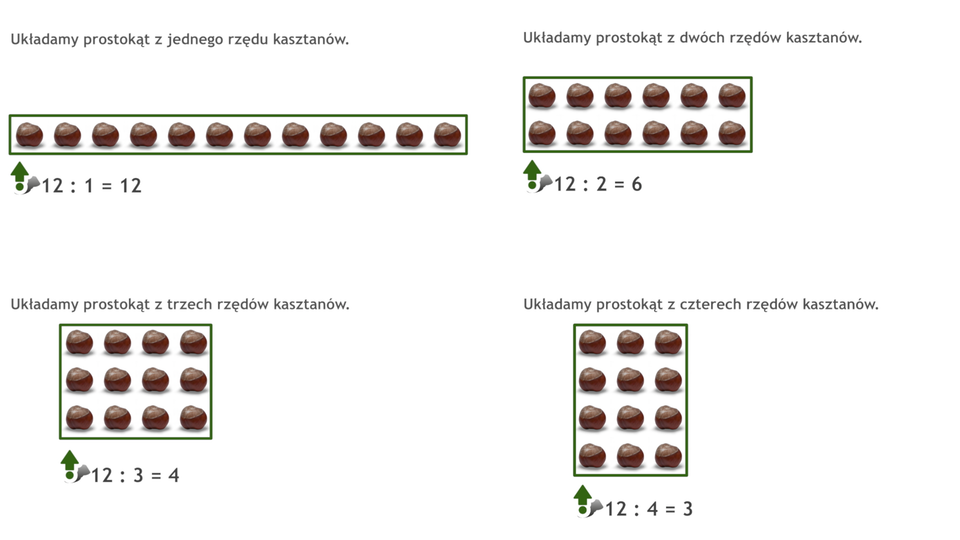
Animacja na przykładzie kasztanów pokazuje, w jaki sposób można podzielić liczbę dwanaście.
A spróbuj z kasztanów ułożyć prostokąt z pięciu rzędów kasztanów. Nie da się!
Argumenty Zosi
Dzielić można też tak:
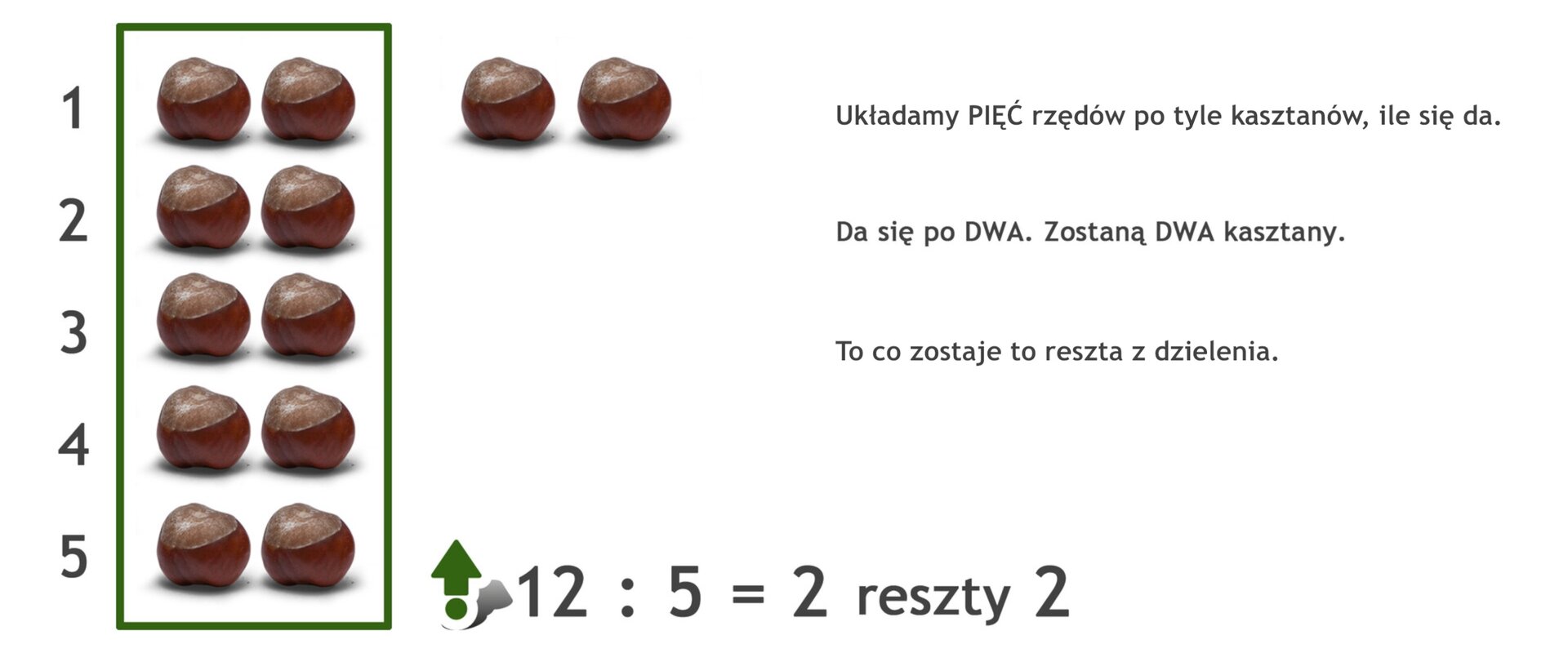
Sądząc po argumentach, Basia najwyraźniej miała na uwadze podzielność liczby przez . Liczba jest podzielna przez , gdy dzieli się przez bez reszty, zatem liczba nie jest podzielna przez . Rację natomiast miała Zosia, co również ładnie zobrazowała. Liczbę można podzielić przez , ale w wyniku dzielenia pozostanie reszta .
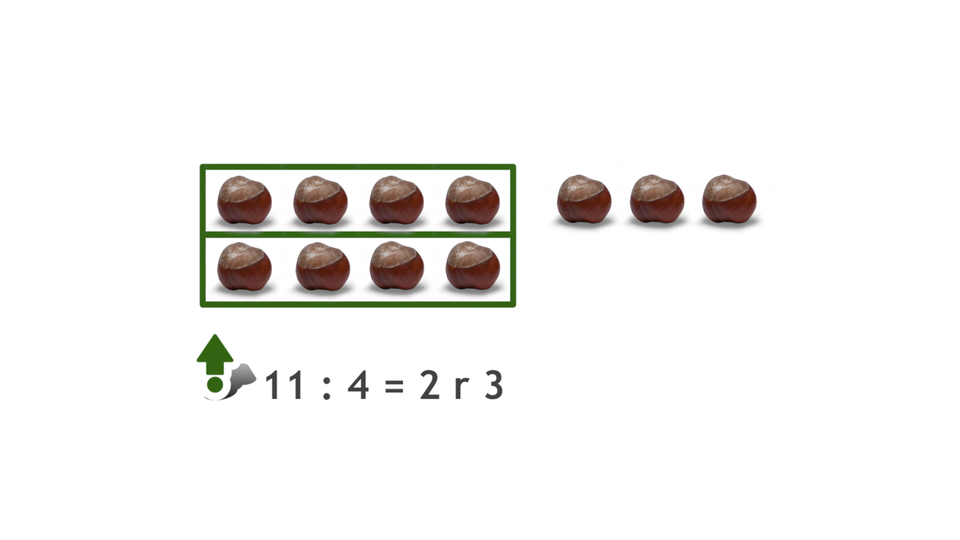
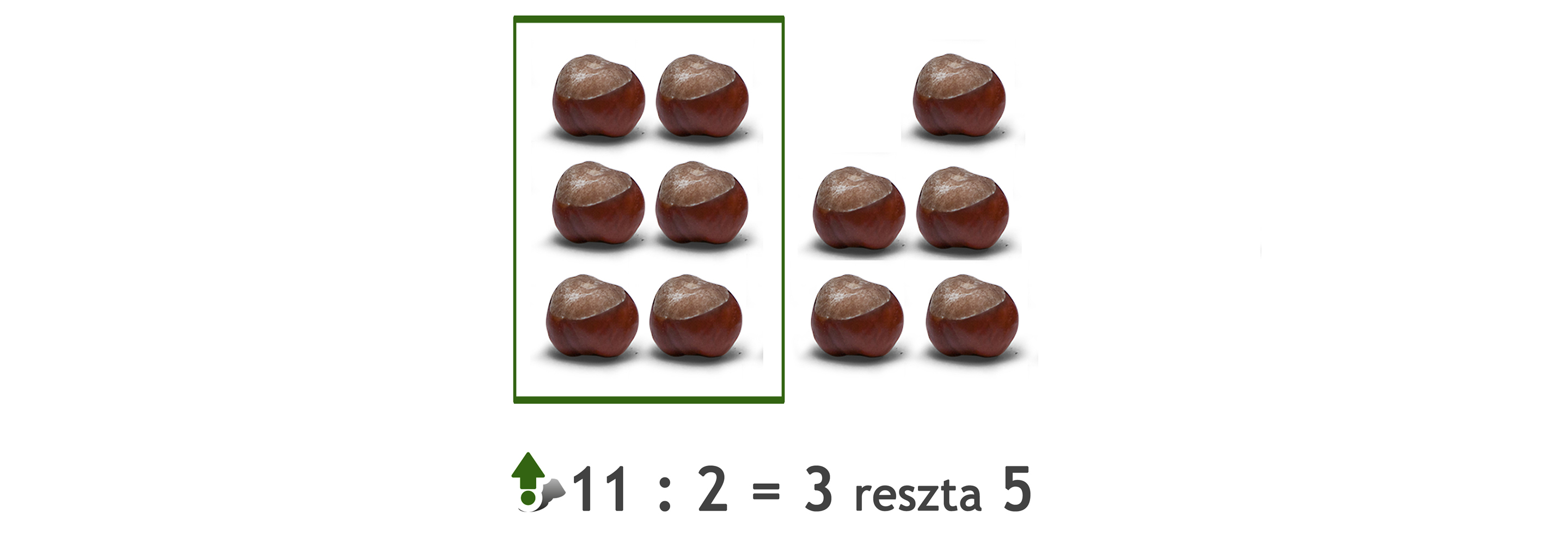
Film dostępny pod adresem /preview/resource/RhJjUrF9tfZKk
Animacja na przykładzie kasztanów pokazuje dzielenie liczby jedenaście z resztą.
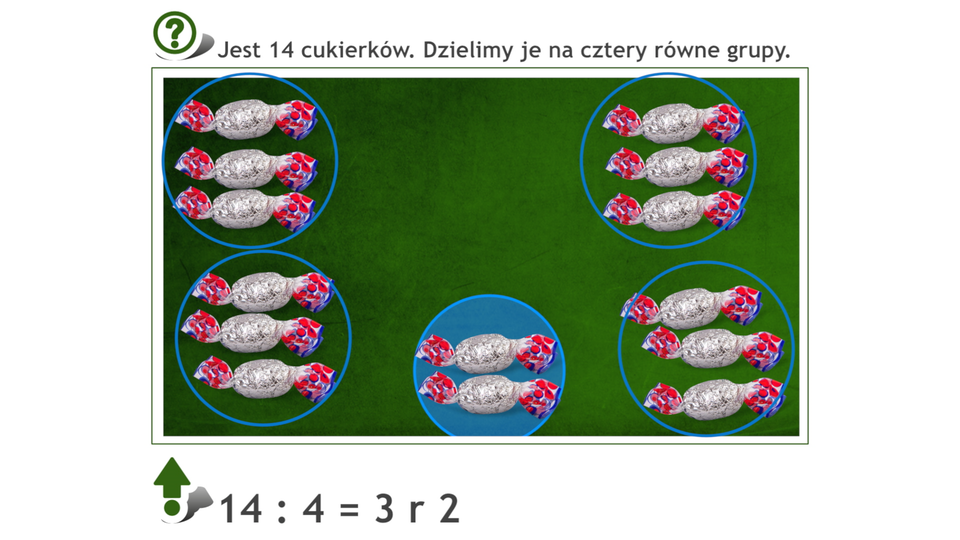
Film dostępny pod adresem /preview/resource/RDZAoLJ0bgHxJ
Animacja na przykładzie cukierków pokazuje dzielenie liczby czternaście z resztą.
Odpowiedź: W jednej kolumnie mogą znajdować się 1. sześciu, 2. , 3. , 4. trzy, 5. , 6. , 7. , 8. , 9. czterech, 10. kasztany oraz 1. sześciu, 2. , 3. , 4. trzy, 5. , 6. , 7. , 8. , 9. czterech, 10. pozostaną poza rzędami.
Basia zebrała kasztany w parku, chce z nich ułożyć prostokąt o jak największej ilości kolumn, po dwa kasztany w każdej.

Basia zebrała kasztanów w parku, chce z nich ułożyć prostokąt o jak największej ilości kolumn, po dwa kasztany w każdej.
- reszta
- reszta
- reszta
- reszta
- reszta
Basia zbierała kasztany w parku, chce z nich ułożyć prostokąt z pięciu kolumn.

Basia zebrała w parku kasztanów, chce z nich ułożyć prostokąt z pięciu kolumn.
- reszta
- reszta
- reszta
- reszta
- reszta
Basia zbierała w parku dziewiętnaście kasztanów, chce z nich ułożyć prostokąt z pięciu kolumn.

Basia zebrała kasztanów w parku, chce z nich ułożyć prostokąt z pięciu kolumn.
- reszta
- reszta
- reszta
- reszta
- reszta
Basia zbierała w parku osiem kasztanów, chce z nich ułożyć prostokąt z trzech kolumn.

Basia zebrała kasztanów w parku, chce z nich ułożyć prostokąt z trzech kolumn.
- reszta
- reszta
- reszta
- reszta
- reszta
Spójrz, ile może wynosić reszta z dzielenia przez .
Reszta musi być zawsze mniejsza od liczby, przez którą dzielimy.
Zaznacz, na którym rysunku poprawnie wykonano dzielenie z resztą.
- 63202
- 63203
- 63205
- 63206
- 63209




Odpowiedź: Oznacza to, że można wykonać 1. , 2. , 3. , 4. , 5. , 6. , 7. zestawy oraz 1. , 2. , 3. , 4. , 5. , 6. , 7. cukierek zostanie nie wykorzystany.
Odpowiedź: Zostaną 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. obwarzanki.
Odpowiedź: W ostatnim rzędzie będzie 1. , 2. , 3. trzech, 4. czterech, 5. , 6. , 7. dwóch, 8. pięciu, 9. , 10. , 11. , 12. żołnierzy.
Odpowiedź: Bez pary zostanie 1. , 2. jeden uczeń, 3. , 4. , 5. , 6. dwóch uczniów, 7. , 8. czterech uczniów, 9. trzech uczniów, 10. .
Odpowiedź: Na wycieczkę szkolną trzeba zamówić 1. pięć, 2. , 3. dwa, 4. , 5. , 6. , 7. , 8. , 9. cztery, 10. trzy autobusy.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

