Pierwiastki
1. Pierwiastki kwadratowe i sześcienne

Uważa się, że grecki filozof Hippazos z Metapontu odkrył, iż długości przekątnej kwadratu o boku 1 nie można zapisać za pomocą liczby wymiernej. Odkrycie było tak niezwykłe, że długi czas utrzymywano je w tajemnicy. Obliczenia Hippazosa doprowadziły do określenia pierwiastków.
Z tego materiału dowiesz się:
co to jest pierwiastek kwadratowy,
co to jest pierwiastek sześcienny,
co to jest liczba podpierwiastkowa,
jak obliczać pierwiastki z niektórych liczb.
Pierwiastek kwadratowy
Zacznijmy od przypomnienia definicji potęgowania i obliczenia kwadratów (drugich potęg) niektórych liczb.
Potęgą liczby o wykładniku naturalnym nazywamy iloczyn czynników, z których każdy jest równy liczbie .
- 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22.
- 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22.
- 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22.
- 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22.
- 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22.
- 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22.
Przeciągnij i upuść.
, , , , , , , , , , , , , , , , , , , , ,
............
............
............
............
............
............
Zauważ, że kwadrat dowolnej liczby wymiernej jest liczbą nieujemną. Natomiast liczba dodatnia może być przedstawiona jako kwadrat liczby dodatniej lub kwadrat liczby ujemnej.
- Liczba jest kwadratem liczby 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. .
- Liczba jest kwadratem liczby 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. .
- Liczba jest kwadratem liczby 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. .
- Liczba jest kwadratem liczby 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. .
- Liczba jest kwadratem liczby 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. .
- Liczba jest kwadratem liczby 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. .
Uzupełnij zapisy, przeciagając takie liczby niedodatnie, aby ich kwadraty miały podaną wartość.
, , , , , , , , , , , , , , , , , ,
............
............
............
............
............
............
Obliczając pierwiastek kwadratowy, będziemy poszukiwać tylko takiej liczby nieujemnej, której kwadrat jest równy danej liczbie nieujemnej.
Szukanie liczby nieujemnej, której kwadrat jest dany, nazywa się obliczaniem pierwiastka kwadratowego z danej liczby nieujemnej.
Pierwiastkiem kwadratowym z liczby nieujemnej nazywamy taką liczbę nieujemną , której kwadrat jest równy liczbie . Pierwiastek ten oznaczamy symbolem .
Pierwiastek kwadratowy nazywany jest również pierwiastkiem stopnia drugiego.
Mówimy, że liczba w wyrażeniu to liczba podpierwiastkowa.
Jeśli i , to , wtedy i tylko wtedy, gdy .
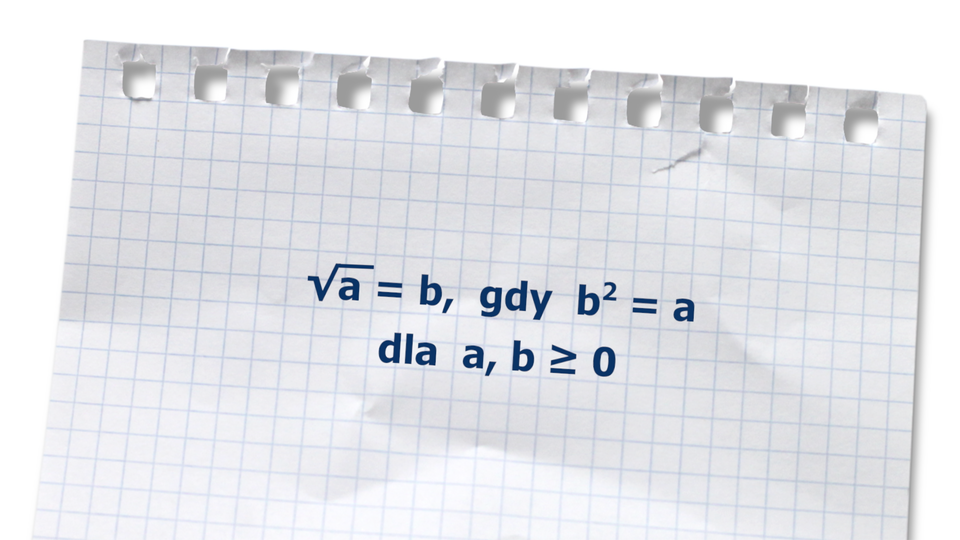
Film dostępny pod adresem /preview/resource/Rl3OVRVEhiKIb
Animacja przedstawia w jaki sposób obliczamy pierwiastek kwadratowy z danej liczby.
Obliczymy pierwiastki podanych liczb.
, bo
, bo
, bo
, bo
, bo
, bo
, bo
, bo
, bo
, bo
, bo
Pierwiastków kwadratowych z liczb ujemnych nie określamy, ponieważ nie znamy takich liczb, które podniesione do kwadratu mają wartość ujemną.
- , , , Tu uzupełnij, Tu uzupełnij, Tu uzupełnij, Tu uzupełnij
- , , , Tu uzupełnij, Tu uzupełnij, Tu uzupełnij, Tu uzupełnij
- , , , Tu uzupełnij, Tu uzupełnij, Tu uzupełnij, Tu uzupełnij
- , , , , Tu uzupełnij, Tu uzupełnij, Tu uzupełnij, Tu uzupełnij, Tu uzupełnij
- Bok kwadratu o polu ma długość Tu uzupełnij .
- Bok kwadratu o polu ma długość Tu uzupełnij .
- Bok kwadratu o polu ma długość Tu uzupełnij .
- Bok kwadratu o polu ma długość Tu uzupełnij .
- Bok kwadratu o polu ma długość Tu uzupełnij .
- Bok kwadratu o polu ma długość Tu uzupełnij .
- Bok kwadratu o polu ma długość Tu uzupełnij .
- Bok kwadratu o polu ma długość Tu uzupełnij .
Pole powierzchni kwadratowego dywanu jest równe powierzchni. Ile taśmy wykończeniowej należy kupić na obszycie brzegów tego dywanu?
Połącz w pary liczby równe.
<span aria-label="jeden początek ułamka, jeden, mianownik, dwa, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>1</mn><mn>2</mn></mfrac></math></span>, <span aria-label="jeden początek ułamka, jeden, mianownik, cztery, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>1</mn><mn>4</mn></mfrac></math></span>, <span aria-label="jeden początek ułamka, trzy, mianownik, cztery, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>3</mn><mn>4</mn></mfrac></math></span>, <span aria-label="jeden początek ułamka, dwa, mianownik, trzy, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>2</mn><mn>3</mn></mfrac></math></span>, <span aria-label="jeden początek ułamka, cztery, mianownik, pięć, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>4</mn><mn>5</mn></mfrac></math></span>, <span aria-label="jeden początek ułamka, dwa, mianownik, pięć, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>2</mn><mn>5</mn></mfrac></math></span>, <span aria-label="jeden początek ułamka, jeden, mianownik, pięć, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>1</mn><mn>5</mn></mfrac></math></span>, <span aria-label="jeden początek ułamka, trzy, mianownik, pięć, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>3</mn><mn>5</mn></mfrac></math></span>, <span aria-label="jeden początek ułamka, jeden, mianownik, trzy, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>1</mn><mn>3</mn></mfrac></math></span>
Pierwiastek sześcienny
Poznamy teraz pierwiastki stopnia trzeciego. Pierwiastki te określone są również dla liczb ujemnych. Najpierw przypomnimy sobie, jak obliczamy potęgi stopnia trzeciego, bowiem pierwiastkowanie i potęgowanie to działania wzajemnie odwrotne.
- 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22.
- 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22.
- 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22.
- 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22.
- 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22.
- 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16. , 17. , 18. , 19. , 20. , 21. , 22.
Przeciągnij i upuść.
, , , , , , , , , , , , , , , , , , , , ,
............
............
............
............
............
............
Szukanie liczby na podstawie danego jej sześcianu nazywa się obliczaniem pierwiastka sześciennego z danej liczby.
Pierwiastkiem sześciennym z liczby nazywamy taką liczbę , której sześcian jest równy liczbie . Pierwiastek ten oznaczamy symbolem .
Pierwiastek sześcienny nazywany jest również pierwiastkiem stopnia trzeciego.
wtedy i tylko wtedy, gdy .

Film dostępny pod adresem /preview/resource/RjZ2rzQyP5QC3
Animacja przedstawia w jaki sposób obliczamy pierwiastek sześcienny z danej liczby.
, bo
, bo
, bo
, bo
, bo
, bo
, bo
, bo
, bo
, bo
, bo
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
- , , , Tu uzupełnij, Tu uzupełnij, Tu uzupełnij, Tu uzupełnij
- , , , Tu uzupełnij, Tu uzupełnij, Tu uzupełnij, Tu uzupełnij
- , , , Tu uzupełnij, Tu uzupełnij, Tu uzupełnij, Tu uzupełnij
Połącz w pary liczby równe.
<span aria-label="jeden początek ułamka, jeden, mianownik, pięć, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>1</mn><mn>5</mn></mfrac></math></span>, <span aria-label="trzy początek ułamka, jeden, mianownik, dwa, koniec ułamka" role="math"><math><mn>3</mn><mfrac><mn>1</mn><mn>2</mn></mfrac></math></span>, <span aria-label="dwa początek ułamka, jeden, mianownik, trzy, koniec ułamka" role="math"><math><mn>2</mn><mfrac><mn>1</mn><mn>3</mn></mfrac></math></span>, <span aria-label="jeden początek ułamka, dwa, mianownik, trzy, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>2</mn><mn>3</mn></mfrac></math></span>, <span aria-label="jeden początek ułamka, jeden, mianownik, sześć, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>1</mn><mn>6</mn></mfrac></math></span>, <span aria-label="dwa początek ułamka, jeden, mianownik, dwa, koniec ułamka" role="math"><math><mn>2</mn><mfrac><mn>1</mn><mn>2</mn></mfrac></math></span>, <span aria-label="jeden początek ułamka, dwa, mianownik, pięć, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>2</mn><mn>5</mn></mfrac></math></span>, <span aria-label="jeden początek ułamka, jeden, mianownik, dwa, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>1</mn><mn>2</mn></mfrac></math></span>, <span aria-label="jeden początek ułamka, trzy, mianownik, pięć, koniec ułamka" role="math"><math><mn>1</mn><mfrac><mn>3</mn><mn>5</mn></mfrac></math></span>
- Sześcian o objętości ma krawędź długości 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. .
- Sześcian o objętości ma krawędź długości 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. .
- Sześcian o objętości ma krawędź długości 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. .
- Sześcian o objętości ma krawędź długości 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. .
- Sześcian o objętości ma krawędź długości 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. .
- Sześcian o objętości ma krawędź długości 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. .
- Sześcian o objętości ma krawędź długości 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. .
Obliczanie wartości pierwiastków
25 = 9 8 3 8 6 3 8 4 3 4 4 5 3 6 3 5 3 4 5 3 9 3 10 7 125 3 = 9 8 3 8 6 3 8 4 3 4 4 5 3 6 3 5 3 4 5 3 9 3 10 7 27 64 3 = 9 8 3 8 6 3 8 4 3 4 4 5 3 6 3 5 3 4 5 3 9 3 10 7 9 64 = 9 8 3 8 6 3 8 4 3 4 4 5 3 6 3 5 3 4 5 3 9 3 10 7 9 16 = 9 8 3 8 6 3 8 4 3 4 4 5 3 6 3 5 3 4 5 3 9 3 10 7 64 3 = 9 8 3 8 6 3 8 4 3 4 4 5 3 6 3 5 3 4 5 3 9 3 10 7 16 = 9 8 3 8 6 3 8 4 3 4 4 5 3 6 3 5 3 4 5 3 9 3 10 7 27 512 3 = 9 8 3 8 6 3 8 4 3 4 4 5 3 6 3 5 3 4 5 3 9 3 10 7
Przeciągnij i upuść.
5 1 16 = 2 2 3 1 1 2 1 3 7 - 1 1 4 1 3 5 1 1 3 - 1 1 2 - 1 3 5 2 1 2 1 5 6 3 1 2
676 1024 1089 1764 44100 729 3 1728 3 4096 3 10648 3 15625 3
64 < = > < = < = > > = > > = < < < > < = 64 3 49 < = > < = < = > > = > > = < < < > < = 9 4 < = > < = < = > > = > > = < < < > < = 8 3 - 25 < = > < = < = > > = > > = < < < > < = - - 125 3 - 1000 3 < = > < = < = > > = > > = < < < > < = - 729 3 - 0,0004 < = > < = < = > > = > > = < < < > < = - 0,008 3
Przeciągnij i upuść.
Uporządkuj liczby w kolejności od najmniejszej do największej.
-
0 3 -
- - 27 64 3 -
9 25 -
1 625 -
0,008 3 -
- 125 3 -
- 1,44 -
25 -
- 1 3
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.