Pierwiastki
2. Szacowanie wyrażeń zawierających pierwiastki
Swobodny spadek to ruch ciała spadającego z pewnej wysokości. Przykładem swobodnego spadku ciała może być skok spadochronowy.

Zakładając, że nie uwględniamy oporu powietrza, czas spadania t możemy wyznaczyć ze wzoru
gdzie h - wysokość początkowa, z której spada ciało, g- wartość przyspieszenia ziemskiego.
Do podanego wzoru najczęściej podstawia się przybliżoną wartość przyspieszenia ziemskiego. Nie zawsze jest też możliwe znalezienie takiej liczby, której druga potęga jest równa liczbie podpierwiastkowej. Zatem czas spadania ciała, zapisany bez użycia pierwiastka będzie liczbą przybliżoną. Do zapisania przybliżonej wartości pierwiastka przyda się umiejętność szacowania wartości pierwiastka. Rozwijaniem tej umiejętności zajmiemy się w tym materiale.
Szacowanie wartości pierwiastka
Oszacujemy wartość pierwiastka drugiego stopnia z trzynastu oraz wartość pierwiastka trzeciego stopnia ze stu.

Film dostępny pod adresem /preview/resource/RgWxMrtJFKkeb
Animacja przedstawia w jaki sposób możemy oszacować wartość pierwiastka z trzynastu.
Oszacujemy wartość pierwiastka drugiego stopnia z trzydziestu.
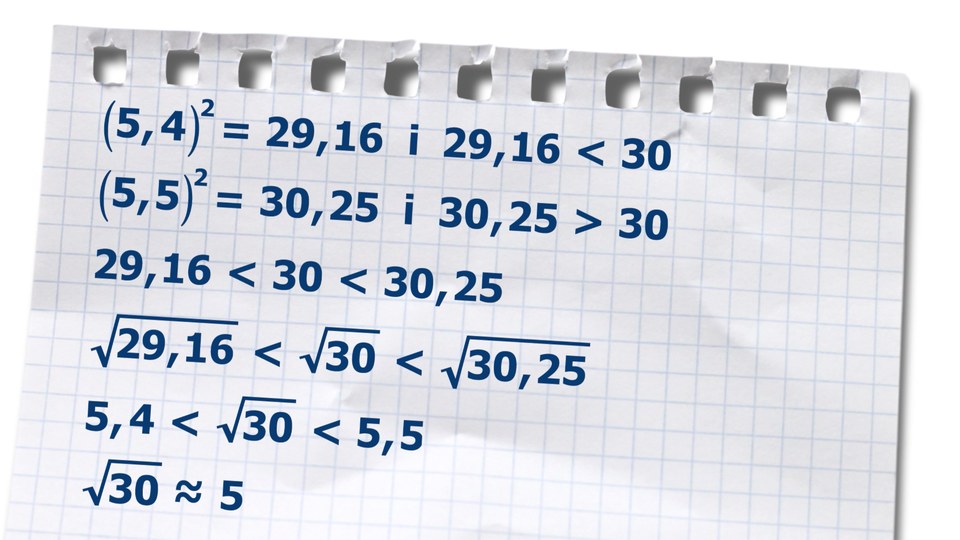
Film dostępny pod adresem /preview/resource/R18xZEDR2zgs4
Animacja przedstawia w jaki sposób możemy wyznaczyć liczbę naturalną, która jest najbliższa pierwiastkowi z trzydziestu.
Oszacujemy wartość pierwiastka trzeciego stopnia z siedmiuset.

Film dostępny pod adresem /preview/resource/R1XRKsHMOZYmd
Animacja przedstawia w jaki sposób możemy wyznaczyć liczbę naturalną, która jest najbliższa pierwiastkowi trzeciego stopnia z siedmiuset.
Liczby niewymierne
Zastanówmy się, ile jest równy . Zgodnie z pojęciem pierwiastka kwadratowego, jest to taka liczba nieujemna, której kwadrat jest równy .
Szukaną liczbą nie jest , ponieważ , ani , ponieważ .
Zatem jest większy od i mniejszy od .
Spróbujmy dokładniej przybliżyć wartość . Obliczmy kwadraty liczb od do .
Ponieważ .
Postępując podobnie, czyli obliczając kwadraty liczb od do , otrzymamy:
Ponieważ , to .
Obliczając kwadraty liczb od do , otrzymamy:
Ponieważ , to:
.
Postępując w podobny sposób, wyznaczymy kolejne cyfry po przecinku, które występują w rozwinięciu dziesiętnym liczby .
Otrzymujemy
W rozwinięciu dziesiętnym liczby nie powtarza się żadna grupa cyfr i cyfr jest nieskończenie wiele. Nie można zapisać liczby w postaci liczby wymiernej.
Zatem liczba ma rozwinięcie dziesiętne nieskończone nieokresowe. Jest ona przykładem liczby niewymiernej. Jej wartość podawana jest najczęściej w przybliżeniu do dwóch miejsc po przecinku i wynosi: .
Przykładami liczb, które mają rozwinięcia dziesiętne nieskończone nieokresowe, są:
Przykładami liczb niewymiernych są pierwiastki kwadratowe z liczb dodatnich, które nie są kwadratami liczb wymiernych i pierwiastki sześcienne z liczb, które nie są sześcianami liczb wymiernych. Na przykład:
Do obliczeń stosuje się ich przybliżenia, najczęściej z dokładnością do dwóch cyfr po przecinku, które otrzymujemy na przykład za pomocą kalkulatora.
Liczba niewymierna to liczba, której nie można przedstawić w postaci ułamka , gdzie , są liczbami całkowitymi i .
Każda liczba niewymierna ma rozwinięcie dziesiętne nieskończone nieokresowe.
Które z podanych liczb są wymierne, a które niewymierne?
Przeciągnij elementy z dolnej sekcji do górnej.
<span aria-label=" minus, pierwiastek sześcienny z minus, początek ułamka, jeden, mianownik, tysiąc, koniec ułamka" role="math"><math><mo>-</mo><mroot><mrow><mo>-</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>1000</mn></mrow></mfrac></mrow><mrow><mn>3</mn></mrow></mroot></math></span>, <span aria-label="pierwiastek sześcienny z minus, sto dwadzieścia jeden" role="math"><math><mroot><mrow><mo>-</mo><mn>121</mn></mrow><mrow><mn>3</mn></mrow></mroot></math></span>, <span aria-label="pierwiastek sześcienny z minus, jeden" role="math"><math><mroot><mrow><mo>-</mo><mn>1</mn></mrow><mrow><mn>3</mn></mrow></mroot></math></span>, <span aria-label="pierwiastek kwadratowy z początek ułamka, dwadzieścia pięć, mianownik, osiem, koniec ułamka" role="math"><math><msqrt><mrow><mfrac><mrow><mn>25</mn></mrow><mrow><mn>8</mn></mrow></mfrac></mrow></msqrt></math></span>, <span aria-label="pierwiastek kwadratowy z dwadzieścia pięć" role="math"><math><msqrt><mrow><mn>25</mn></mrow></msqrt></math></span>, <span aria-label="początek ułamka, pierwiastek kwadratowy z cztery, mianownik, trzy, koniec ułamka" role="math"><math><mfrac><mrow><msqrt><mrow><mn>4</mn></mrow></msqrt></mrow><mrow><mn>3</mn></mrow></mfrac></math></span>, <span aria-label="pierwiastek kwadratowy z sto dwadzieścia jeden" role="math"><math><msqrt><mrow><mn>121</mn></mrow></msqrt></math></span>, <span aria-label="pierwiastek sześcienny z początek ułamka, osiem, mianownik, sześćdziesiąt cztery, koniec ułamka" role="math"><math><mroot><mrow><mfrac><mrow><mn>8</mn></mrow><mrow><mn>64</mn></mrow></mfrac></mrow><mrow><mn>3</mn></mrow></mroot></math></span>, <span aria-label="pierwiastek kwadratowy z jeden przecinek cztery" role="math"><math><msqrt><mrow><mn>1,4</mn></mrow></msqrt></math></span>, <span aria-label="pierwiastek sześcienny z minus, dwadzieścia siedem" role="math"><math><mroot><mrow><mo>-</mo><mn>27</mn></mrow><mrow><mn>3</mn></mrow></mroot></math></span>, <span aria-label="pierwiastek kwadratowy z pięć" role="math"><math><msqrt><mrow><mn>5</mn></mrow></msqrt></math></span>, <span aria-label="pierwiastek kwadratowy z dziewięć" role="math"><math><msqrt><mrow><mn>9</mn></mrow></msqrt></math></span>, <span aria-label="pierwiastek kwadratowy z dziewięć przecinek zero dziewięć" role="math"><math><msqrt><mrow><mn>9,09</mn></mrow></msqrt></math></span>, <span aria-label="początek ułamka, dwadzieścia trzy, mianownik, pierwiastek sześcienny z osiem, koniec ułamka" role="math"><math><mfrac><mrow><mn>23</mn></mrow><mrow><mroot><mrow><mn>8</mn></mrow><mrow><mn>3</mn></mrow></mroot></mrow></mfrac></math></span>
| liczby wymierne | |
|---|---|
| liczby niewymierne |
Wybierz liczby niewymierne.
Porównajmy liczby oraz .
Na początku szacujemy liczbę , czyli szukamy dwóch pierwiastków, których wartości są liczbami całkowitymi, a które znajdują się na osi liczbowej najbliżej liczby .
Zatem
Następnie przekształcamy nierówność tak, aby otrzymać szacowane wyrażenie.
Stąd otrzymujemy, że
-
40 -
50 -
130 3 -
215 3
- Tu uzupełnij
< 7 < - Tu uzupełnij
< 15 < - Tu uzupełnij
< 91 < - Tu uzupełnij
< 153 < - Tu uzupełnij
< 680 < - Tu uzupełnij
< 11 3 < - Tu uzupełnij
< - 29 3 < - Tu uzupełnij
< - 78 3 < - Tu uzupełnij
< 200 3 < - Tu uzupełnij
< 342 3 <
Połącz w pary liczbę niewymierną i liczbę naturalną, która jest jej najbliższa.
<math><mn>9</mn></math>, <math><mn>5</mn></math>, <math><mn>4</mn></math>, <math><mn>8</mn></math>, <math><mn>3</mn></math>, <math><mn>10</mn></math>, <math><mn>6</mn></math>, <math><mn>12</mn></math>
2 2 ≈ 4 3 ≈ 2 - 3 ≈ 3 + 1 ≈ 2 + 3 ≈ 2 - 3 ≈ 2 2 - 4 3 ≈ 5 2 - 5 ≈ 6 - 2 3 ≈
-
31 -
33 -
34 -
35 -
24 -
37
-
26 -
27 -
29 -
30 -
25 -
36
-
257 -
260 -
262 -
267 -
273 -
280 -
285 -
288 -
289 -
256 -
255 -
290
-
401 -
409 -
411 -
432 -
426 -
430 -
437 -
440 -
400 -
441 -
443 -
398
-
28 3 -
30 3 -
41 3 -
46 3 -
50 3 -
61 3 -
27 3 -
64 3 -
66 3 -
25 3
-
218 3 -
334 3 -
252 3 -
300 3 -
316 3 -
243 3 -
216 3 -
343 3 -
215 3 -
346 3
-
1121 3 -
1011 3 -
1330 3 -
1265 3 -
1191 3 -
1223 3 -
1000 3 -
1331 3 -
1421 3 -
999 3
18 + 7 5 3 6 7 40 3 5 20 + 20 40 4 65 3 16 80 3 - 10 3 70 3 10 + 30 3 40 600 3 + 250 3 210
Uporządkuj liczby kolejności rosnącej.
-
3 + 15 -
17 + 1 -
2 + 19 -
10 + 5 -
14 + 3
- 1.
44 8 3 17 13 42 13 3 39 3 12 3 19 12 11 7 3 18 14 3 9 3 38 3 40 40 3
Przeciągnij i upuść.
............
............
............
............
............
............
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.