Długość okręgu i pole koła
1. Długość okręgu
Nie sposób nie dostrzec na poniższym zdjęciu szeregu obiektów geometrycznych, w szczególności okręgów i ich łuków.

Te obiekty tworzą maswerk – geometryczny wzór architektoniczny o charakterze dekoracyjnym, wykuty z kamienia lub zrobiony z cegieł, używany do wypełnienia górnej części gotyckiego okna, witrażu, rozety itp.
Nie musimy jednak od razu jechać do Wenecji, by podziwiać kunszt ówczesnych budowniczych katedr – wystarczy wybrać się chociażby do Malborka. Również tam znajdziemy maswerki, których przewodnim motywem architektonicznym są okręgi, na przykład takie, jak na poniższym zdjęciu.

Poniższy szkic pokazuje elementy konstrukcji maswerków z malborskiego zamku.
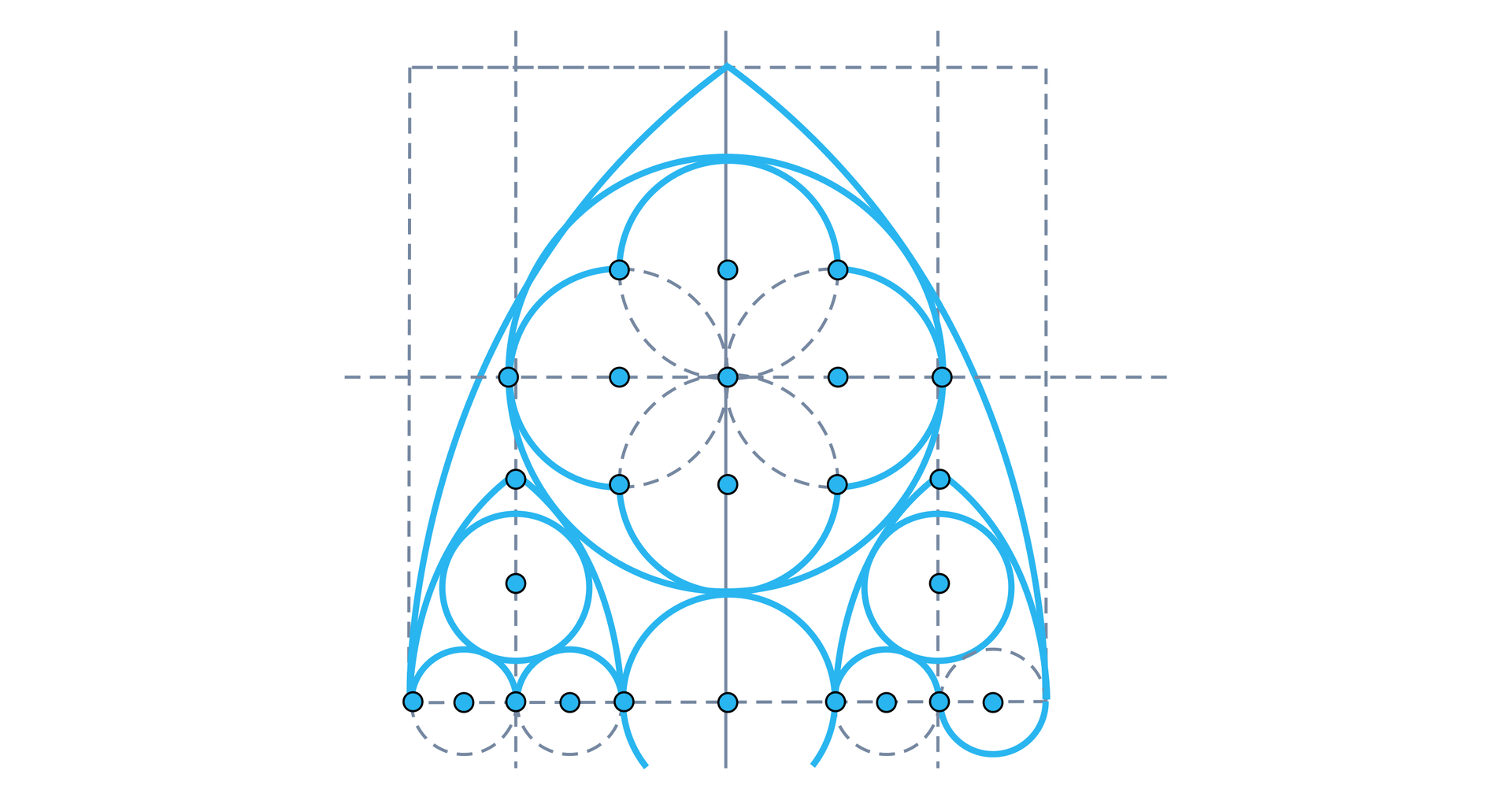
Już bardzo dawno temu uczeni poszukiwali wzoru pozwalającego obliczyć długość okręgu. Zauważyli oni, że stosunek długości okręgu do długości średnicy jest dla dowolnego okręgu zawsze taki sam.
W tym materiale będziesz korzystać ze wzoru na długość okręgu w rozwiązywaniu problemów teoretycznych i praktycznych.
Okrąg
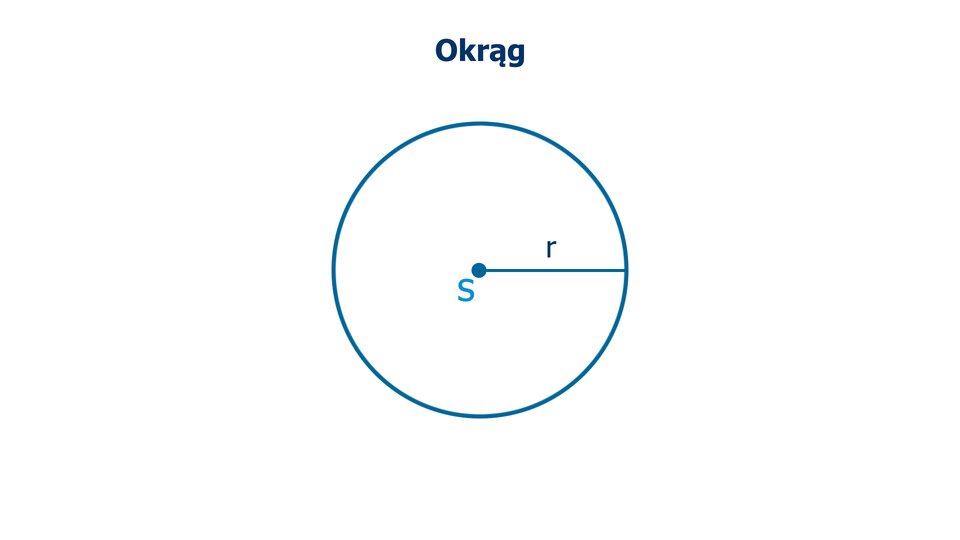
Film dostępny pod adresem /preview/resource/R1ZWWaC0z6ZjA
Animacja pokazuje, czym jest okrąg.
Okręgiem o środku w punkcie i promieniu nazywamy zbiór wszystkich punktów płaszczyzny, których odległość od punktu jest równa .
Okrąg o środku w punkcie i promieniu oznaczamy .

Długość okręgu
Przez wiele stuleci uczeni poszukiwali wzoru pozwalającego określić długość okręgu, którego promień jest znany. Dokonując przybliżonych pomiarów, zauważyli, że stosunek długości okręgu do jego średnicy jest w każdym przypadku w przybliżeniu równy .
Zapoznaj się z poniższym apletem.
Zapoznaj się z opisem poniższego apletu.
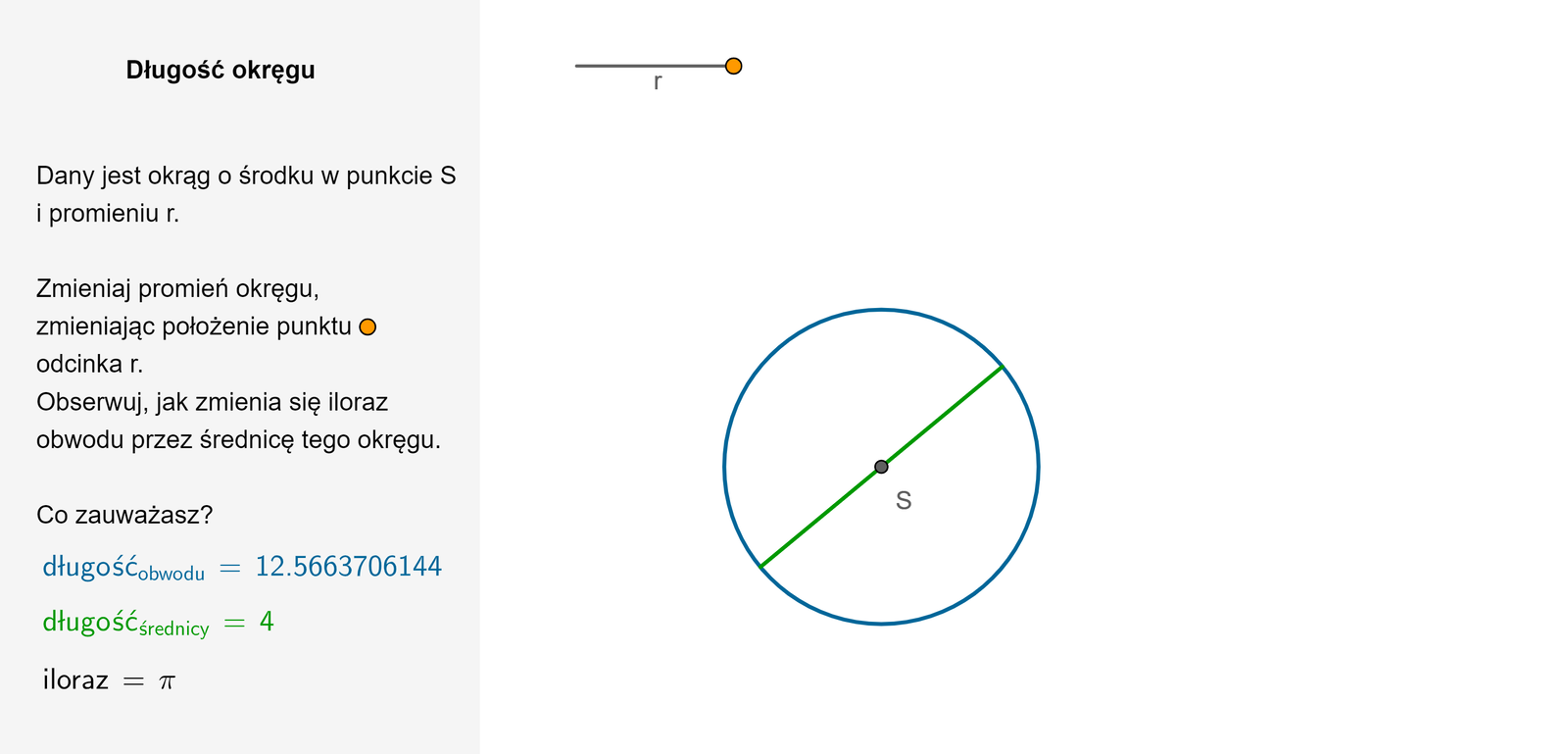
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DSFlckvhd
Przeprowadzony eksperyment pozwolił na znalezienie dokładniejszej liczby określającej stosunek długości okręgu do jego średnicy.
Liczbę tę w w. oznaczono grecką literą od pierwszej litery greckiego słowa perimetron, czyli obwód.
Oznaczmy:
– długość okręgu,
– promień okręgu.
Wtedy średnica okręgu jest równa oraz
Długość okręgu o promieniu wyraża się wzorem .
Zapoznaj się z poniższym apletem.
Zapoznaj się z opisem poniższego apletu.
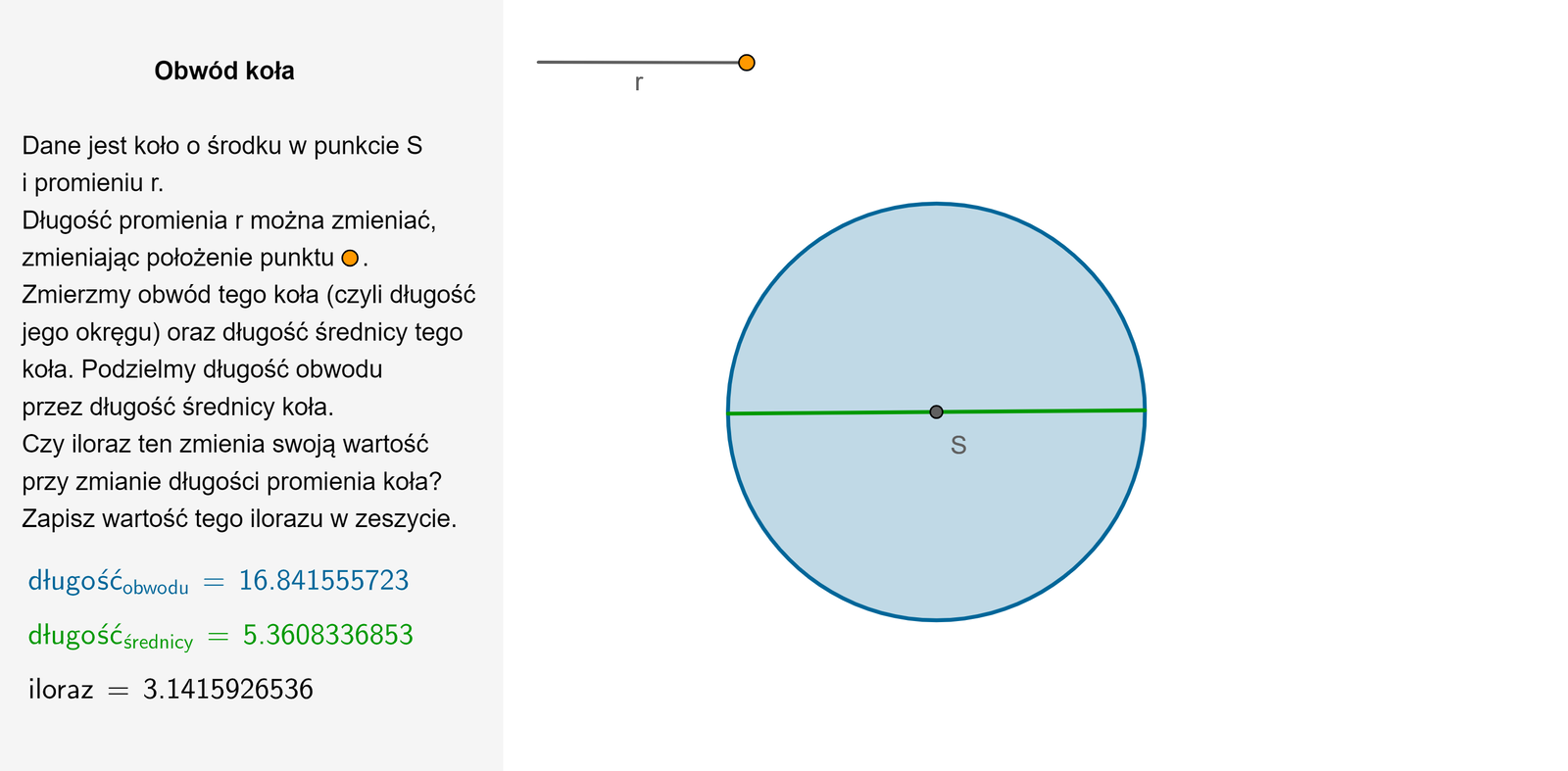
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DSFlckvhd
Liczba
Starożytni Egipcjanie przyjmowali, że stosunek obwodu koła do jego średnicy jest równy
Średniowieczni Chińczycy uważali, że jest on równy
Przez wieki podawano coraz lepsze przybliżenie liczby .
W w. matematyk holenderski Ludolph van Ceulen [Ludolf fan keule] podał jej wartość z dokładnością do miejsc po przecinku:
Na cześć tego matematyka liczba pi zwana jest też ludolfiną.
W w. udowodniono, że liczba nie jest liczbą wymierną. Nie da się jej zatem zapisać w postaci ułamka dziesiętnego skończonego, ani w postaci ułamka dziesiętnego nieskończonego okresowego.
Obecnie znamy przybliżenie liczby z dokładnością do kilku bilionów miejsc po przecinku.
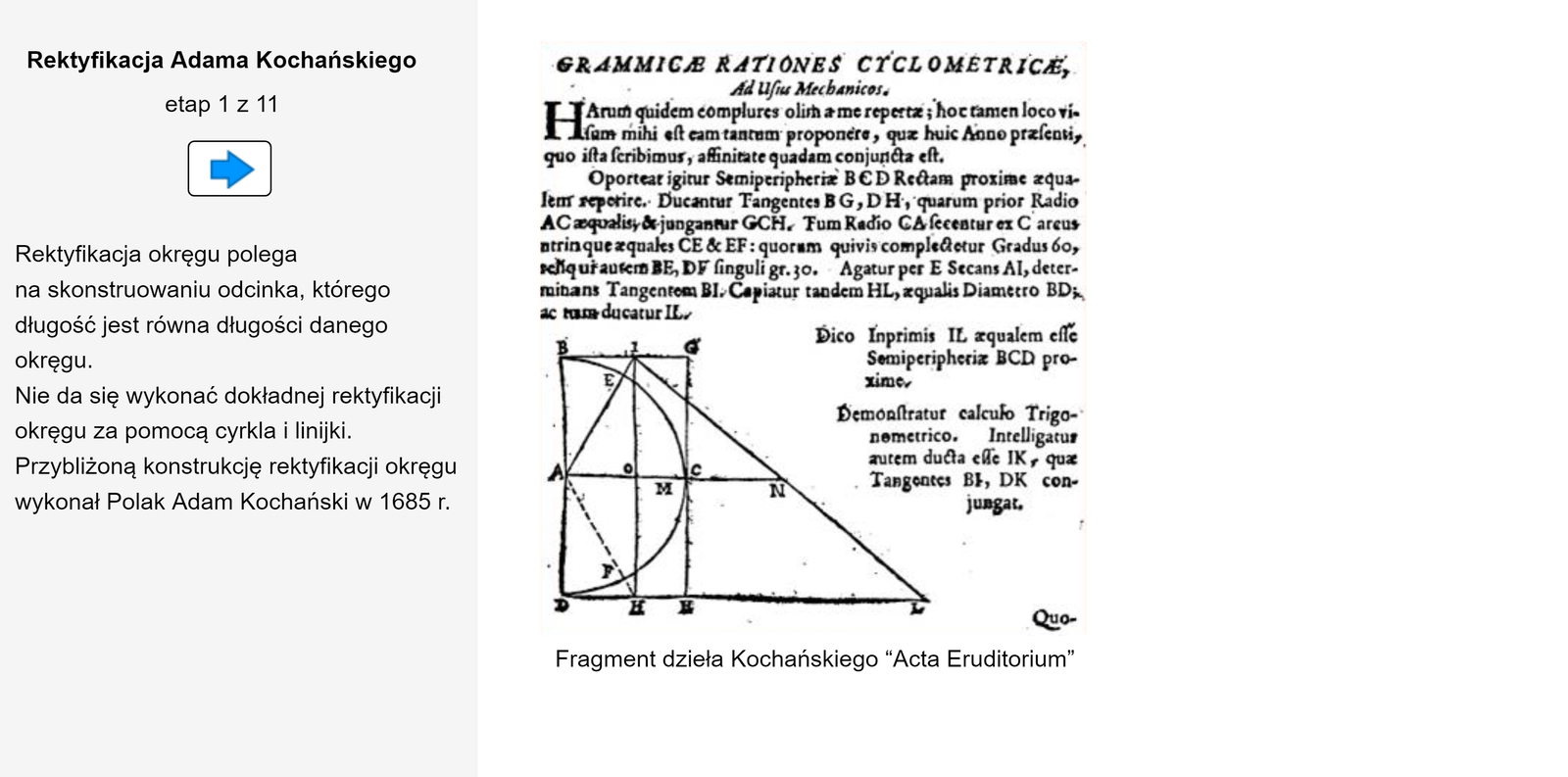
Rektyfikacja koła
Rektyfikacja lub wyprostowanie okręgu polega na skonstruowaniu odcinka, którego długość jest równa obwodowi danego okręgu.
Jedną z przybliżonych konstrukcji wyprostowania okręgu podał w r. Adam Kochański, nadworny matematyk króla Jana Sobieskiego.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DSFlckvhd
W w. p.n.e. rzymski architekt Witruwiusz zaproponował sposób pomiaru odległości drogowych, wykorzystujący poruszający się rydwan. Koło takiego rydwanu miało promień . Na pokonanie jednej mili rzymskiej musiało wykonać obrotów.

Oblicz wartość liczby , przyjmowaną przez Witruwiusza.
Rozwiązanie:
W obliczeniach praktycznych najczęściej przyjmuje się, że .
Średnica kółka do deskorolki jest równa . Obliczymy, ile razy obróci się to kółko na drodze długości .
Rozwiązanie:
Obliczamy długość drogi, jaką pokona kółko podczas jednego obrotu, czyli obwód kółka.
Zamieniamy metr na milimetry.
Obliczamy, ile razy obróci się kółko.
Kółko obróci się około razy.
Obliczymy długość okręgu o promieniu .
Rozwiązanie:
Korzystamy ze wzoru na długość okręgu, tym razem nie zastępując liczby jej wartością przybliżoną.
Długość okręgu jest równa .
Obliczymy przybliżoną długość promienia koła o obwodzie .
Rozwiązanie:
Oznaczymy przez przybliżoną długość (w ) promienia koła i skorzystamy ze wzoru ma długość okręgu.
Promień koła ma około długości.
Koniec dużej wskazówki zegara w ciągu godziny pokonał drogę długości . Obliczymy przybliżoną długość tej wskazówki.
Rozwiązanie:
Oznaczmy przez długość (w ) dłuższej wskazówki zegara i skorzystajmy ze wzoru na obwód koła.
Wskazówka ma około długości.
Basia spakowała prezent dla swojej siostry w rulon o średnicy . Czy starczy jej wstążki na obwiązanie tego prezentu w dwóch miejscach skoro na węzeł i kokardę potrzeba ?
Rozwiązanie:
Zaczniemy od obliczenia obwodu rulonu.
Wyznaczymy do tego jego promień, czyli
.
Zatem obwód rulonu jest równy
.
Na jedno obwiązanie potrzeba , zatem na dwa .
Oznacza to, że Basi nie starczy wstążki na obwiązanie prezentu w dwóch miejscach.
Sprawdzimy, czy z drutu o długości można uformować trzy obręcze, każda o promieniu ?
Rozwiązanie:
Najpierw obliczymy obwód jednej obręczy.
.
Zatem na trzy obręcze potrzeba:
.
Oznacza to, że drutu nie wystarczy na wykonanie trzech obręczy o promieniu każda.
Która z figur ma większy obwód: okrąg o promieniu , czy trójkąt równoboczny o boku długości ?
Rozwiązanie:
Zacznijmy od wyznaczenia obwodu okręgu, czyli
.
Obwód trójkąta jest równy .
Wynika stąd, że obwód okręgu jest większy od obwodu trójkąta równobocznego.
Odpowiedź: Promień koła wynosi 1. , 2. , 3. , 4. , 5. .
Odpowiedź: Średnica kosza wynosi około Tu uzupełnij.
- Jeśli dwa okręgi mają równe promienie, to są przystające.
- Jeśli dwa okręgi mają równe obwody, to są współśrodkowe.
- Długość okręgu wyraża się zawsze liczbą wymierną.
- Dla każdego okręgu stosunek jego obwodu do średnicy jest stały.
- jest mniejszy od
- jest równy
- większy od
Odpowiedź: Wstążka powinna mieć długość okołó 1. , 2. , 3. , 4. , 5. , 6. .
Oblicz, ile razy obwód koła o promieniu jest większy od: długości okręgu o średnicy
Odpowiedź: Obwód jest większy Tu uzupełnij razy. długości okręgu o promieniu
Odpowiedź: Obwód jest większy Tu uzupełnij razy.
Odpowiedź: Długość okręgu zwiększy się Tu uzupełnij razy.
Oblicz obwód zacieniowanej figury przedstawionej na rysunku.
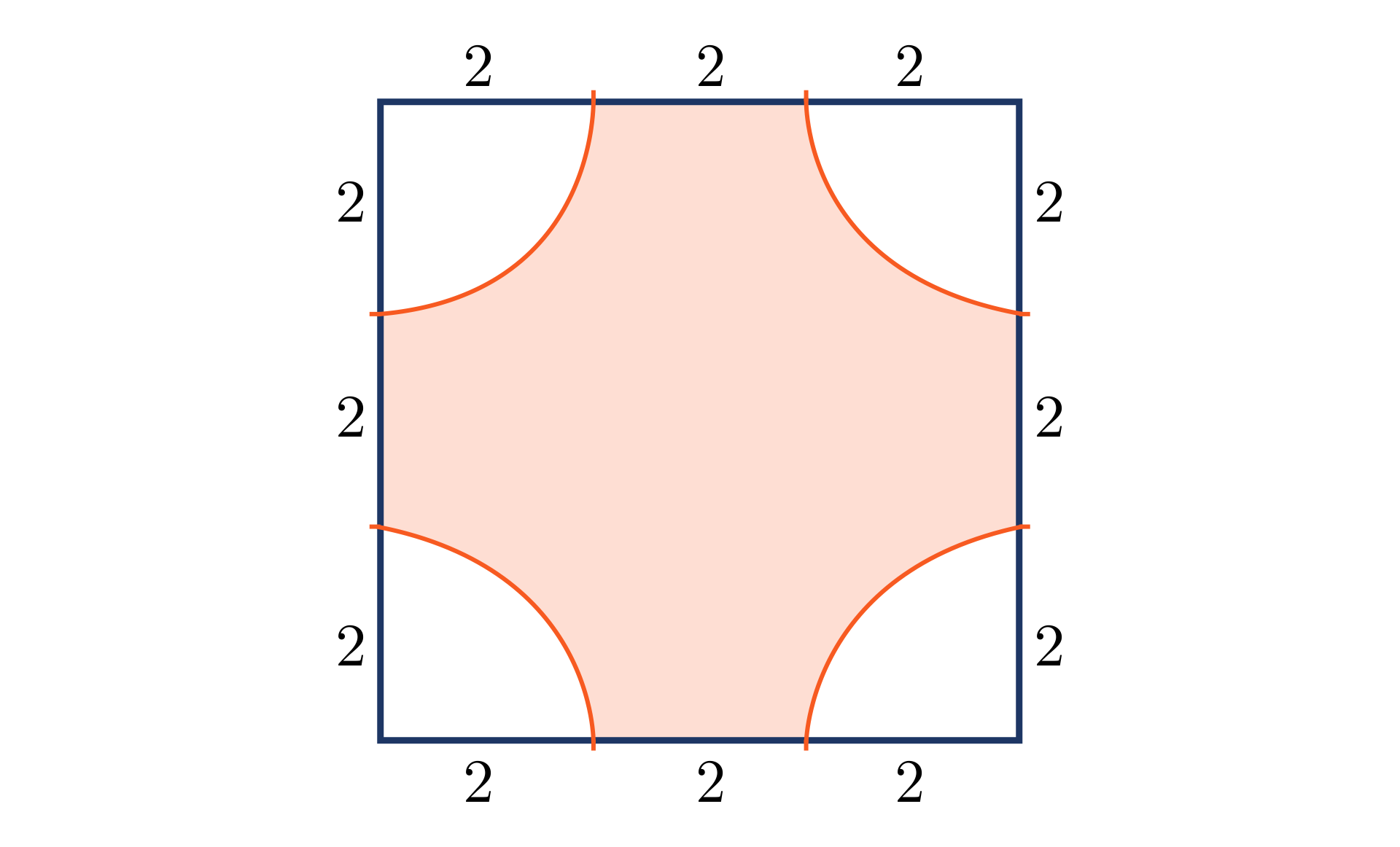
- Suma obwodu kwadratu o boku długości i obwodu połowy okręgu o promieniu długości wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .
- Różnica obwodu trójkąta równobocznego o boku długości i obwodu czwartej części okręgu o średnicy długości wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .
- Suma obwodu prostokąta o bokach długości i oraz obwodu trzeciej części okręgu o promieniu długości wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .
- Różnica obwodu rombu o boku długości i obwodu połowy okręgu o średnicy długości wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .
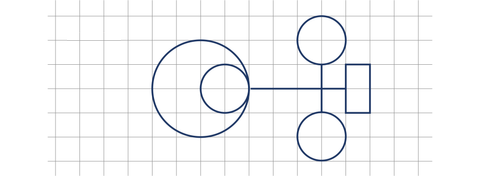
Oblicz łączną długość narysowanych linii. Przyjmij długość jednej kratki jako odcinek jednostkowy.
Tomek zwinął mapę Polski w rulon o średnicy . Ile sznurka potrzebuje na związanie tego rulonu, jeżeli na kokardę potrzebuje dodatkowo sznurka?
Martyna postanowiła ogrodzić swój ogródek w kształcie ćwiartki koła o promieniu . Siatka ogrodzeniowa pakowana jest w rolkach po . Ile paczek musi kupić Martyna, aby ogrodzić swój ogród, uwzględniając miejsce na furtkę szerokości ? Przyjmij .
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.