Długość okręgu i pole koła
2. Pole koła, pole pierścienia kołowego
Już w starożytności genialny twórca i myśliciel – Archimedes – zaznaczył swój wkład w rozwój matematyki. W traktacie „O mierzeniu okręgu” pokazał, że pole koła jest równe polu trójkąta równoramiennego, którego podstawą jest odcinek o długości równej obwodowi koła, a wysokością jest promień koła.
Problemem starożytnej matematyki greckiej była również kwadratura koła - czyli skonstruowanie kwadratu, którego pole jest równe polu danego koła.
Czy problem szkoły pitagorejskiej udało się rozwiązać, czy też okazało się to niemożliwe?
W tym materiale zajmiemy się zastosowaniem wzoru na pole koła, aby pogłębiać wiedzę i analizować starożytne problemy geometrii.
Koło
Film dostępny pod adresem /preview/resource/RBG3Q91VBXxVo
Animacja przedstawia rysowanie koła o środku w punkcie S oraz promieniu R za pomocą cyrkla.
Kołem o środku w punkcie i promieniu r nazywamy zbiór tych punktów płaszczyzny, których odległość od punktu jest mniejsza bądź równa .

– koło o środku w punkcie i promieniu
Pole koła
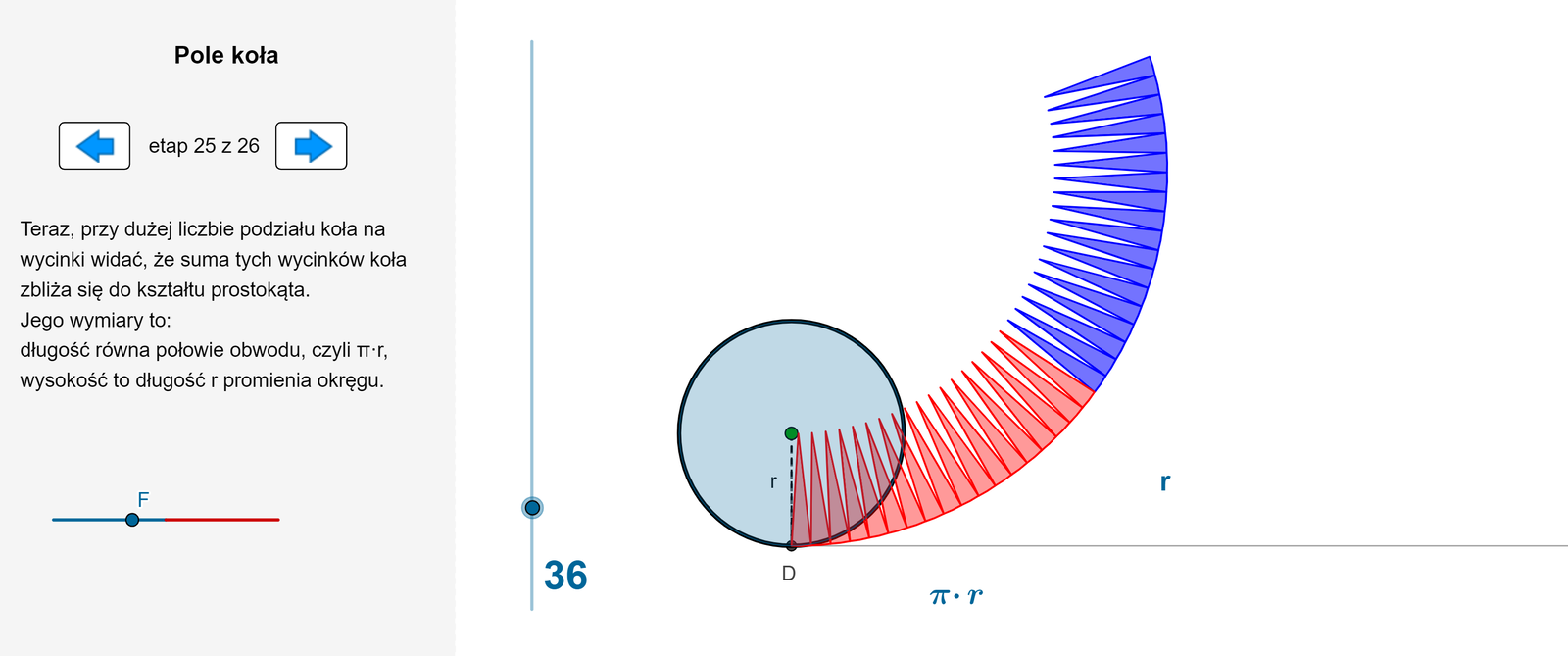
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DpvTj9cFG
Pole koła o promieniu jest równe iloczynowi liczby i kwadratu promienia.

Obliczanie pola koła
Oblicz pole koła o promieniu .
Do wzoru na pole koła wstawiamy .
Pole koła jest równe .
Obwód małego znaku zakazu wynosi . Oblicz, ile blachy potrzeba na jego wykonanie.

Obliczymy najpierw promień koła, w kształcie którego jest znak – korzystamy ze wzoru na obwód koła.
Korzystamy ze wzoru na pole koła.
Przyjmijmy , wtedy
Na wykonanie małego znaku zakazu potrzeba około blachy.
Pole powierzchni jednego okrągłego konfetti jest równe . Ile takich konfetti można wyciąć z kwadratowej kartki papieru o boku długości ?
Obliczamy najpierw średnicę koła, w kształcie którego jest konfetti.
bo . Mamy
Ponieważ , zatem w kwadracie o boku zmieści się kół o średnicy każde.
Z kwadratowej kartki można wyciąć konfetti.
Hania, Lena i Zosia wybrały się do pizzerii. Hania zamówiła małą pizzę z pomidorami o średnicy , a Lena i Zosia wspólną dużą pizzę z szynką o średnicy .
Ile razy pizza Leny i Zosi jest większa od pizzy Hani?
Rozwiązanie:
Pizza Hani ma średnicę , czyli
Zatem pole pizzy Hani wynosi:
Analogicznie obliczymy pole drugiej pizzy.
zatem
Aby obliczyć, ile razy pizza Leny i Zosi jest większa od pizzy Hani wykonamy działanie:
Pizza Leny i Zosi jest razy większa od pizzy Hani.
Tymon i Kuba zamówili w pizzerii okrągłą pizzę o średnicy , która została podzielona na osiem takich samych kawałków. Tymon zjadł pięć kawałków pizzy, a Kuba trzy kawałki. O ile większa była porcja, którą zjadł Tymon od porcji Kuby?
Pani Kwiatkowska wygospodarowała w swoim ogrodzie dwie rabaty: pierwszą w kształcie prostokąta o bokach długości i oraz drugą, w kształcie koła o promieniu . W której rabacie pani Kwiatkowska może posadzić więcej bratków?
Rozwiązanie:
Obliczymy pole prostokątnej rabaty.
Pole prostokątnej rabaty wynosi zatem .
Obliczymy pole okrągłej rabaty.
Pole okrągłej rabaty wynosi zatem .
Pani Kwiatkowska posadzi więcej bratków w rabacie w kształcie prostokąta.
Na działce w kształcie kwadratu o boku Pani Bratkowska wygospodarowała rabatę o kształcie koła o promieniu . Jakim procentem działki jest rabata?
Adam i Karol chcą zamówić pizzę na kolację. Adam twierdzi, że bardziej opłaca się zamówić największą pizzę o średnicy za złotych. Karol twierdzi, że bardziej opłaca się kupić dwie pizze, z których każda ma średnicę i kosztuje złotych. Który z nich ma rację?
Rozwiązanie
Aby sprawdzić, która opcja bardziej się opłaca, obliczymy pola, jakie mają pizze. Zauważmy, że w obu przypadkach rachunek wyniesie tyle samo, więc wystaczy porównać pola pizz.
Pierwsza pizza ma średnicę , przy czym
.
Przekształcamy równość, podstawiamy liczby i otrzymujemy promień pizzy.
Teraz obliczymy pole pizzy.
Pizze w drugiej opcji mają średnicę , przy czym
.
Przekształcamy równość, podstawiamy liczby i otrzymujemy promień pizzy.
Teraz obliczymy pole jednej pizzy.
Nie zapominamy o tym, że w drugim przypadku zamówione zostałyby dwie pizze.
, zatem to Adam ma rację.
Obliczymy, czy większy promień ma kolorowa nalepka w kształcie koła o polu , czy czarno‑biała nalepka w kształcie koła o obwodzie ?
Rozwiązanie
Najpierw obliczymy promień kolorowej nalepki o danym polu.
bo .
Analogicznie obliczymy promień czarno‑białej nalepki o danym obwodzie.
bo .
Ponieważ , zatem druga nalepka ma większy promień.
Obliczymy pole zaznaczonej części figury.
Przyjmiemy, że pole jednej kratki jest równe .
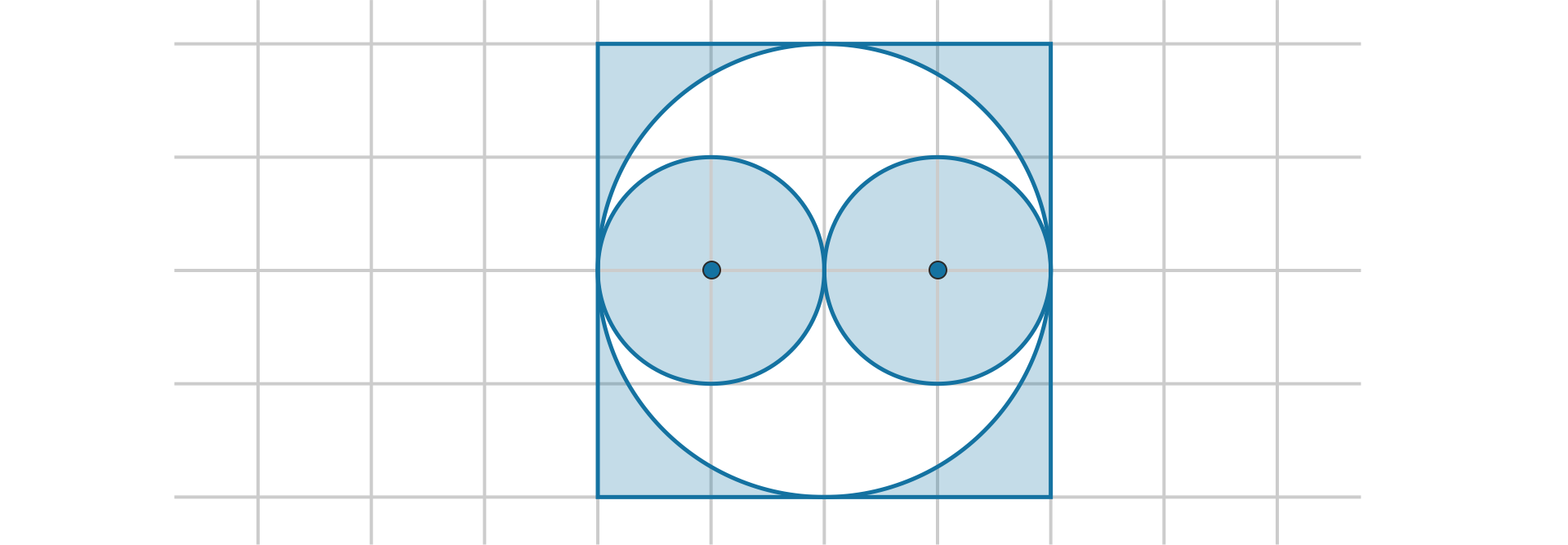
Rozwiązanie:
Najpierw obliczymy pole mniejszego okręgu o promieniu .
Pole okręgu o promieniu jest równe:
Pole kwadratu o boku jest równe:
Pole zamalowanej części () obliczymy ze wzoru:
Pole zamalowanej części jest równe .
Pierścieniem kołowym nazywamy część płaszczyzny, która jest ograniczona przez dwa współśrodkowe okręgi.
Pole pierścienia kołowego obliczamy ze wzoru:
Promień mniejszego z kół na rysunku jest równy , a większego .

Obliczymy pole zaznaczonego pierścienia.
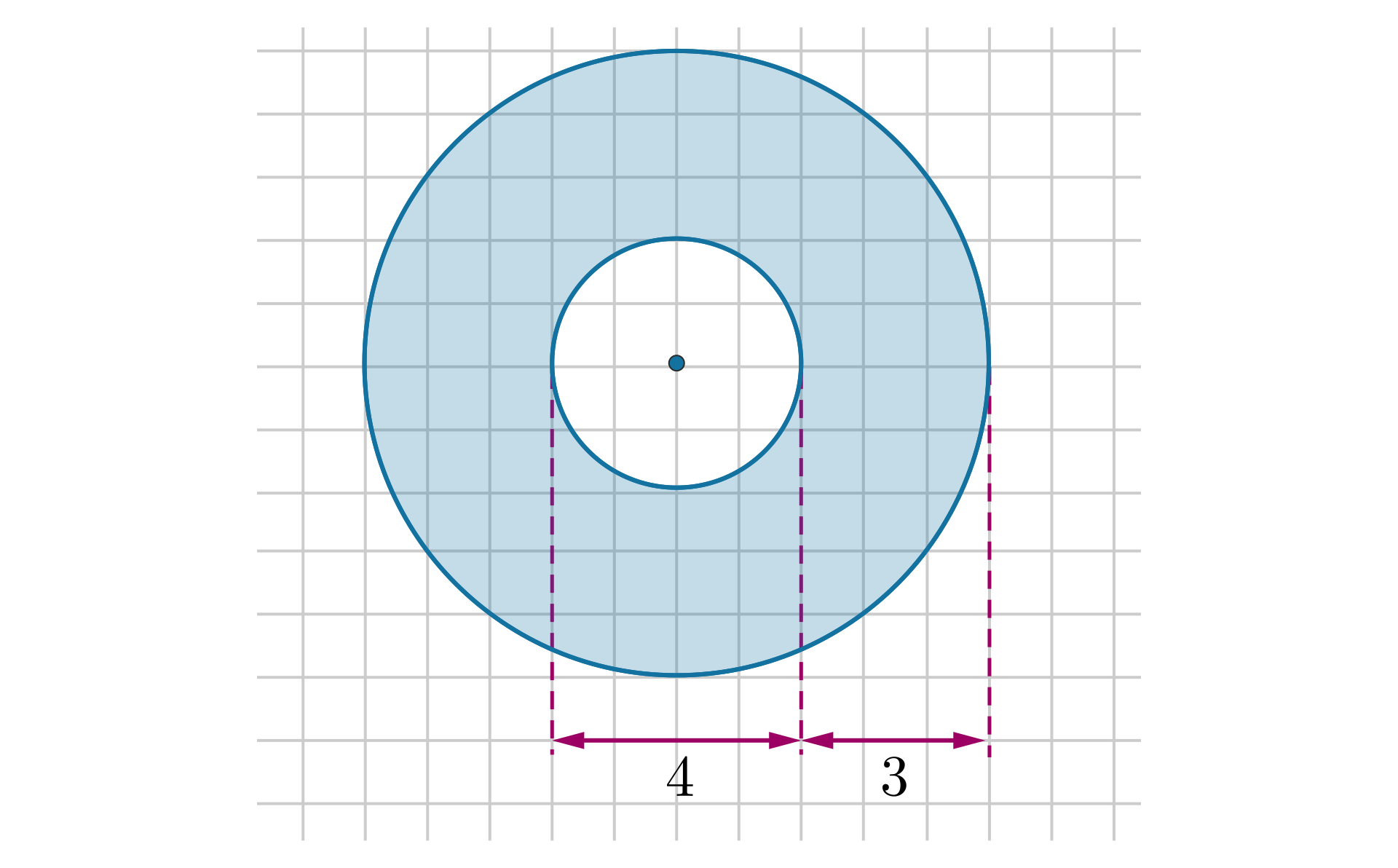
Rozwiązanie:
Z rysunku odczytujemy, że promień mniejszego koła jest równy .
Promień drugiego koła jest równy:
Pole pierścienia kołowego obliczymy ze wzoru:
Pole pierścienia jest równe .
Wokół klombu w kształcie koła o średnicy ogrodnik wykonał brukowany chodnik o szerokości . Obliczymy, jaką powierzchnię ma chodnik.
Rozwiązanie:
Powierzchnię chodnika obliczymy korzystając ze wzoru na pole pierścienia kołowego.
Promień klombu wynosi .
Promień okręgu utworzonego przez klomb wraz z chodnikiem wynosi .
Zatem
Chodnik ma powierzchnię około .
- około
- około
- około
- około
Przyjmij, że pole zielonego kwadratu jest równe .

- Pole koła jest większe od .
- Obwód koła jest mniejszy od .
- Pole kola jest mniejsze od .
- Obwód kola jest większy od .
- Jeśli dwa koła mają równe pola, to są przystające.
- Jeśli dwa koła są współśrodkowe, to mają równe pola.
- Pole koła wyraża się zawsze liczbą niewymierną.
- Liczba wyrażająca pole koła może być równa liczbie wyrażającej obwód tego koła.
Obwód koła jest równy . Pole tego koła jest równe 1. , 2. , 3. , 4. , 5. , 6. .
Oblicz pole zacieniowanej figury przedstawionej na rysunku.

Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.