Aplet
Zapoznaj się z prezentacją, w której przedstawiono algorytm Forda‑Fulkersona. Zadaniem tego algorytmu jest rozwiązanie problemu maksymalnego przepływu.
Pamiętaj, że wierzchołki grafu można oznaczać w różny sposób. W tej sekcji oznaczamy je wielkimi literami.
Algorytm Forda‑Fulkersona kończy swoje działanie, gdy nie istnieje ścieżka rozszerzająca. W momencie, gdy algorytm się zatrzyma, przepływ netto jest maksymalnym przepływem sieci.
Zaprezentowana symulacja interaktywna pokazuje działanie algorytmu Forda‑Fulkersona na wprowadzonym grafie. Zbadaj przepływ grafów przedstawionych w tym e‑materiale, a następnie spróbuj wykorzystać symulację do zweryfikowania problemu niezawodności sieci.
Na początku na grafie znajdują się przepustowości danych kanałów, a ponieważ przepływy równe są 0, jest to równoznaczne z siecią rezydualną.
Zwróć uwagę na to, że w symulacji wierzchołki oznaczamy cyframi. To rozwiązanie jest poprawne – tak jak przedstawione w prezentacji oznaczenia literowe.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D12IkD9Sc
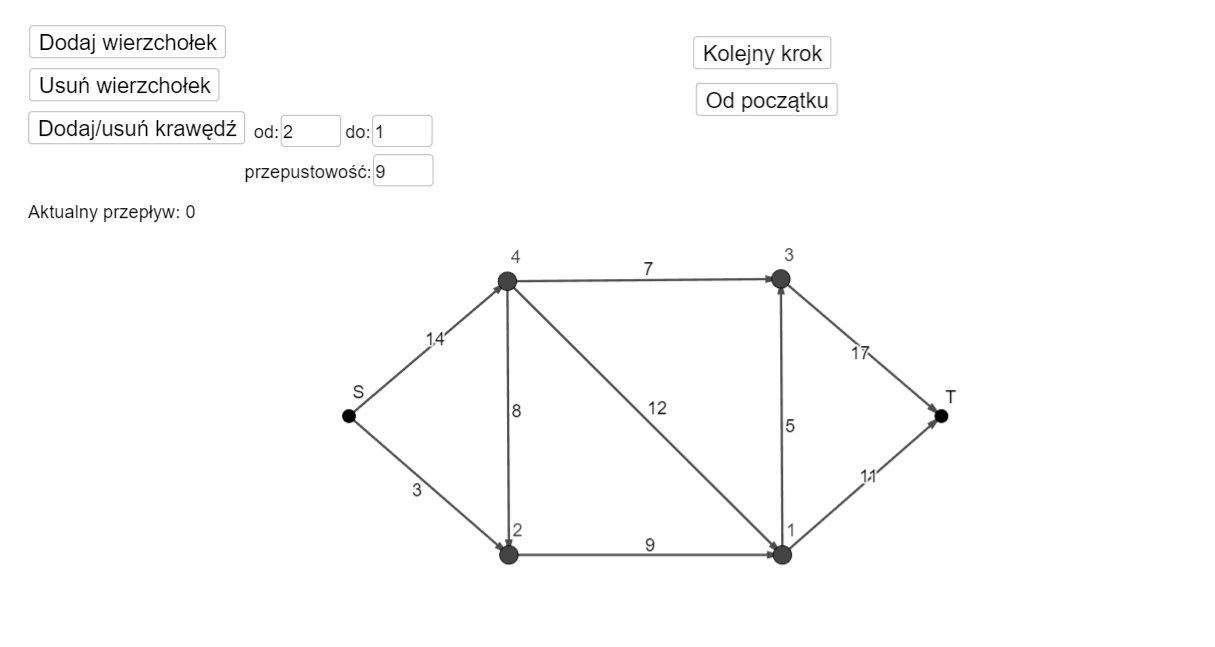
Aplet przedstawia działanie algorytmu Forda- Fulkersona na grafie. Dzięki przyciskom apletu możliwe jest dodanie oraz usunięcie wierzchołka, dodanie lub usunięcie krawędzi pomiędzy poszczególnymi wierzchołkami. Na ekranie znajdują się również przyciski następny krok oraz od początku. Na ekranie po ustaleniu wszystkich wartości pojawia się odpowiednia ilość wierzchołków z czego jeden z nich jest oznaczony literą S a drugi literą T, pozostałe wierzchołki są ponumerowane.
Przykład pierwszy. Graf składa się z trzech punktów, z lewej strony znajduje się punkt S, z prawej punkt T, pomiędzy nimi znajduje się punkt podpisany jako jeden. Pomiędzy S i jeden znajduje się strzałka z liczbą 9 . Pomiędzy jeden i T znajduje się strzałka z liczbą 11. Aktualny przepływ jest równy 0.
Krok pierwszy:
Aktualny przepływ: 0.
Nad strzałkami pojawiają się dodatkowe liczby: nad strzałką S jeden jest to 0 9, a nad strzałką od jeden do T 0 11 . Na grafie pojawiają się dodatkowe dwie strzałki narysowane linią przerywaną o zwrotach przeciwnych do strzałek narysowanych linią ciągłą. Nad strzałką prowadzącą od T do jeden znajdują się liczby 0 11. Nad strzałką od jeden do S 0 0.
Krok drugi:
Maksymalny możliwy przepływ na znalezionej ścieżce : 9 .
Strzałki prowadzące od S do jeden i od jeden do T zmieniają swój kolor na czerwony.
Krok trzeci:
Aktualny przepływ: 9 .
Wszystkie strzałki na grafie zmieniły kolor na niebieski. Nad strzałką od S do jeden znajdują się wartości 9 9, a nad strzałką od jeden do T: 9 11 . Nad strzałkami narysowanymi liniami przerywanymi znajdują się wartości 9 0.
Krok czwarty:
Zakończono algorytm. Maksymalny przepływ wynosi: 9 .
Nad strzałką prowadzącą od S do jeden znajduje się wartość: 9 9 . Nad strzałką prowadzącą od jeden do T znajduje się wartość 9 11 .Przykład drugi. Graf składa się z czterech punktów, są to S, dwa, jeden oraz T. Pomiędzy punktami znajdują się strzałki, nad którymi znajdują się następujące wartości. Od S do dwa wartość 3, od dwa do jeden wartość 9, od jeden to T wartość 11 .
Krok pierwszy:
Aktualny przepływ: 0.
Nad strzałkami pojawiają się dodatkowe liczby: S dwa 0 3. Od dwa do jeden 0 9, od jeden do T 0 11 . Na grafie pojawiają się dodatkowe trzy strzałki narysowane linią przerywaną o zwrotach przeciwnych do strzałek narysowanych linią ciągłą. Nad każdą z tych strzałek zapisano wartość: 0 0.
Krok drugi:
Aktualny przepływ: 0.
Możliwy przepływ na znalezionej ścieżce: 3 .
Strzałki na grafie narysowane linią ciągłą zostały zaznaczone na czerwono.
Krok trzeci:
Aktualny przepływ 3.
Nad strzałką od S do dwa znajduje się wartość 3 3, nad strzałką od dwa do jeden 3 9, nad strzałką od jeden do T artość 3 11 . Wartości nad strzałkami przerwanymi wynoszą minus 3 0.
Krok czwarty:
Zakończono algorytm. Maksymalny przepływ wynosi: 3 .
Na grafie wartości nad strzałkami są następujące: Od S do dwa wartość 3 3, od dwa do jeden 3 9, od jeden do T 3 11 .Przykład trzeci. Graf składa się z sześciu punktów: S, jeden, dwa, trzy, cztery oraz T. Punkty od jeden do cztery zostały umieszczone na wierzchołkach kwadratu, punkt S znajduje się po lewej a punkt T po prawej stronie. Pomiędzy punktami znajdują się strzałki podpisane w następujący sposób: pomiędzy S i cztery znajduje się wartość 14, pomiędzy S i dwa wartość 3, pomiędzy cztery i dwa wartość 8, pomiędzy cztery i jeden wartość 12, pomiędzy cztery i trzy wartość 7, pomiędzy jeden i trzy wartość 5, pomiędzy trzy i T wartość 17, pomiędzy jeden i T wartość 1 . Na początku aktualny przepływ wynosi zero.
Krok pierwszy:
Aktualny przepływ: 0.
Na grafie zmieniają się opisy strzałek, każda z nich jest opisana jako zero liczba. Liczby po ukośniku są tożsame z liczbami początkowymi. Nad każdą ze strzałek pojawiła się strzałka namalowana linią przerywaną mająca zwrot przeciwny to strzałki narysowanej linią ciągłą. Nad każdą z tych strzałek znajduje się zapis 0 0.
Krok drugi:
Aktualny przepływ: 0.
Możliwy przepływ na znalezionej ścieżce: 3 .
Kolorem czerwonym zaznaczone zostały strzałki: od S do dwa, od dwa do jeden, od jeden do trzy oraz od trzy do T.
Krok trzeci:
Aktualny przepływ: 3 .
Ścieżka mająca wcześniej kolor czerwony zmieniła barwę na niebieską. Wartości nad poszczególnymi strzałkami mają następujące wartości: S dwa 3 3, dwa jeden wartość 3 9, jeden trzy 3 5, trzy T wartość 3 17 . Niebieskie strzałki namalowane linią przerywaną mają zapisane nad sobą wartości 3 0.
Krok czwarty:
Aktualny przepływ: 3 .
Możliwy przepływ na znalezionej ścieżce: 2 .
Kolorem czerwonym zaznaczona zostaje ścieżka od S do cztery, od cztery do jeden, od jeden do trzy od trzy do T.
Krok piąty:
Aktualny przepływ: 5 .
Kolor ścieżki został zmieniony na kolor niebieski. Wartości są następujące: od S do cztery 2 14, od cztery o jeden 2 12, od jeden do trzy 5 5, od trzy do T 5 17 . Strzałki namalowane linią przerywaną mają nad sobą zapisane wartości minus 2 0.
Krok szósty:
Aktualny przepływ: 5 .
Możliwy przepływ na znalezionej ścieżce: 10 .
Kolorem czerwonym zaznaczona została ścieżka: od S do cztery, od cztery do jeden od jeden do T.
Krok siódmy:
Aktualny przepływ: 15 .
Kolor ścieżki został zmieniony na kolor niebieski. Wartości na strzałkach są następujące: od S do cztery 12 14, od cztery do jeden 12 12, od jeden do T 10 11 . Nad strzałkami namalowanymi liniami przerywanymi znajduje się wartość 12 0.
Krok ósmy:
Aktualny przepływ: 15 .
Możliwy przepływ na znalezionej ścieżce: 1
Pojawia się ścieżka w kolorze czerwonym od S do cztery, od cztery do dwa od dwa do jeden oraz od jeden do T.
Krok dziewiąty:
Aktualny przepływ: 16 .
Ścieżka zmienia kolor na niebieski. Wartości są następujące: od S do cztery 13 14, od cztery do dwa 1 8, od dwa do jeden 4 9. Od jeden do T 11 11. Wartości nad liniami przerywanymi są następujące: od cztery do S 13 0, od dwa do cztery 1 0. Od jeden do dwa 4 0. Od T do jeden 11 0.
Krok dziesiąty:
Aktualny przepływ: 16 .
Możliwy przepływ na znalezionej ścieżce: 1 .
Kolorem czerwonym zaznaczona zostaje ścieżka od S do cztery od cztery do trzy od trzy do T.
Krok jedenasty:
Aktualny przepływ: 17 .
Ścieżka zmienia kolor na kolor niebieski. Wartości nad strzałkami są następujące: od S do cztery 14 14, od cztery do trzy 1 7, od trzy do T 6 17. Wartości nad strzałkami namalowanymi liniami przerywanymi są następujące: od cztery do S 14 0. Od trzy do cztery 1 0, od T do trzy 6 0.
Krok dwunasty:
Zakończono algorytm. Maksymalny przepływ wynosi: 17 .
Wartości na grafie są następujące: od S do dwa 3 3, od S do cztery 14 14, od cztery do dwa 1 8, od cztery do jeden 12 12 od cztery do trzy 1 7 od dwa do jeden 4 9, od jeden do trzy 5 5, od jeden do T 11 11 . Od trzy do T 6 17 .