Wielokrotności

RbbAJpHOQe0rv1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przykład 1

Spójrz na fragment chodniczka liczbowego. Co wspólnego mają liczby umieszczone na niebieskich polach?

R1IuDCfLPOxZV1

Ważne!

Liczby: $0, 3, 6, 9$ , … to kolejne wielokrotności liczby $3$ . Każda wielokrotność jest wynikiem mnożenia liczby naturalnej przez liczbę $3$ , np.

0 ∙ 3 = 0

1 ∙ 3 = 3

2 ∙ 3 = 6

Nie możemy wypisać wszystkich wielokrotności liczby $3$ , jest ich bowiem nieskończenie wiele.
Liczba zero jest najmniejszą wielokrotnością liczby $3$ , jak również każdej innej liczby naturalnej.

Ćwiczenie 1

Wypisz pięć dowolnych wielokrotności liczby

$7$
$12$
$15$
$31$

Ćwiczenie 2

Na dywaniku $100$ liczb zaznacz wszystkie wielokrotności liczby $5$ większe od $20$ , a mniejsze od $60$ .

Tabela. Dane
$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$10$
$11$	$12$	$13$	$14$	$15$	$16$	$17$	$18$	$19$	$20$
$21$	$22$	$23$	$24$	$25$	$26$	$27$	$28$	$29$	$30$
$31$	$32$	$33$	$34$	$35$	$36$	$37$	$38$	$39$	$40$
$41$	$42$	$43$	$44$	$45$	$46$	$47$	$48$	$49$	$50$
$51$	$52$	$53$	$54$	$55$	$56$	$57$	$58$	$59$	$60$
$61$	$62$	$63$	$64$	$65$	$66$	$67$	$68$	$69$	$70$
$71$	$72$	$73$	$74$	$75$	$76$	$77$	$78$	$79$	$80$
$81$	$82$	$83$	$84$	$85$	$86$	$87$	$88$	$89$	$90$
$91$	$92$	$93$	$94$	$95$	$96$	$97$	$98$	$99$	$100$

$25, 30, 35, 40, 45, 50$

Ćwiczenie 3

Współrzędne punktów zaznaczonych na osi liczbowej są wielokrotnościami liczby $23$ . Odczytaj współrzędne punktów $A, B, C, D, E$ .

RfeYM3GD9Jxn01

"Rysunek osi liczbowej z zaznaczonymi punktami A, B, C, D, E oraz punktem 23. Między 23 a punktem E zaznaczono jedenaście równych części. Szukane punkty: punkt A wyznacza pierwszą część za punktem 23 — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

$A = 46$
$B = 92$
$C = 161$
$D = 230$
$E = 276$

classicmobile

Ćwiczenie 4

Sprawdź za pomocą kalkulatora, czy liczba $11151$ jest wielokrotnością podanej liczby. Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

REw13Vlhm7xCT

Liczba $11151$ jest wielokrotnością liczby $7$ .
Liczba $11151$ jest wielokrotnością liczby $13$ .
Liczba $11151$ jest wielokrotnością liczby $11$ .
Liczba $11151$ jest wielokrotnością liczby $9$ .

static

Ćwiczenie 4

Sprawdź za pomocą kalkulatora, czy liczba $11151$ jest wielokrotnością podanej liczby. Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

RoywQHt4DJvWh

Liczba $11151$ jest wielokrotnością liczby $7$ .
Liczba $11151$ jest wielokrotnością liczby $13$ .
Liczba $11151$ jest wielokrotnością liczby $11$ .
Liczba $11151$ jest wielokrotnością liczby $9$ .

Ćwiczenie 5

Wypisz $12$ kolejnych, różnych od zera:

wielokrotności liczby $5$
wielokrotności liczby $6$
wspólnych wielokrotności liczb $5$ i $6$
Podaj najmniejszą wspólną wielokrotność liczb $5$ i $6$ .

wielokrotności $5$ : $5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60$
wielokrotności $6$ : $6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72$
wspólne wielokrotności: $30, 60$
najmniejsza wspólna wielokrotność liczb $5$ i $6$ : $30$

Ćwiczenie 6

Wyznacz.

$NWW (2, 3)$
$NWW (3, 4)$
$NWW (5, 10)$
$NWW (2, 9)$
$NWW (6, 8)$
$NWW (6, 9)$

$6$
$12$
$10$
$18$
$24$
$18$

Ćwiczenie 7

Jaką najmniejszą długość powinien mieć sznurek, aby można go było pociąć na kawałki długości $20 cm$ lub $25 cm$ ?

$100 cm$

Ćwiczenie 8

Janek i Wojtek przygotowywali się do zawodów lekkoatletycznych i biegali dookoła boiska. Wojtek przebiegał ten dystans w ciągu $5$ minut, a Janek w ciągu $4$ minut. Chłopcy o godzinie $14.00$ wystartowali równocześnie z tego samego miejsca i pobiegli w tę samą stronę. O której godzinie spotkają się ponownie na starcie?

$14 : 20$

Ćwiczenie 9

Dwa statki jednocześnie wypływają z portu. Pierwszy z nich odbywa ośmiodniowe rejsy, drugi zaś – rejsy trwające $12$ dni. Za ile dni statki znów spotkają się w porcie?

$24$

iqaILn75qv_d5e445

Dzielniki

Przykład 2

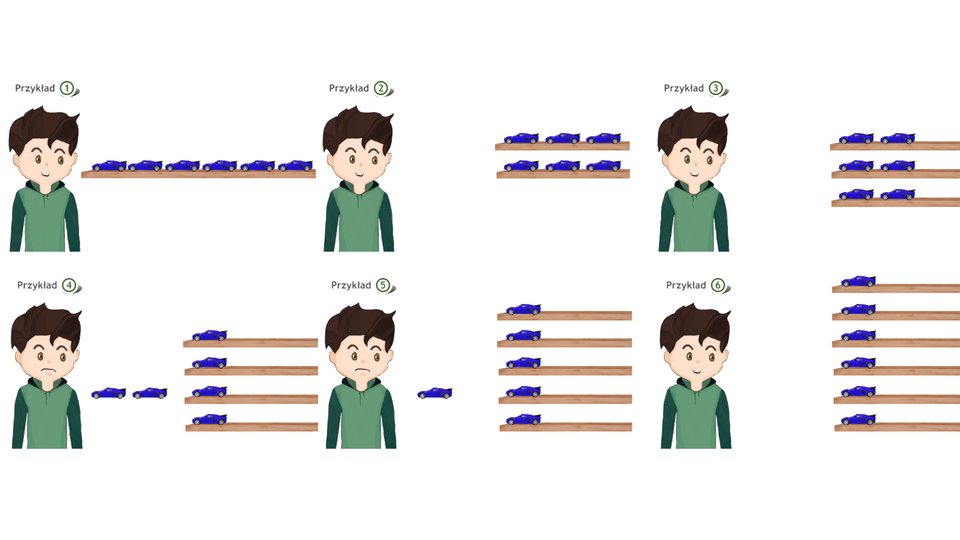
Adaś ma $6$ samochodzików, które postanowił poukładać na regale, tak by na każdej półce było ich tyle samo. Pomóż Adasiowi poukładać na różne sposoby samochodziki na półkach. Sprawdź, ile półek w regale Adaś może wykorzystać.
Wykorzystaj

jedną półkę
dwie półki
trzy półki
cztery półki
pięć półek
sześć półek

R1KVwy7v6v0Ri1

Ważne!

Liczba $6$ dzieli się bez reszty przez $1, 2, 3$ i $6$ . Mówimy, że liczby $1, 2, 3, 6$ są dzielnikami liczby $6$ .
Liczba $6$ jest podzielna przez $1, 2, 3$ i $6 .$
Liczba $6$ nie jest podzielna przez $4$ i $5$ , bo reszta z dzielenia nie jest równa zero.

Ćwiczenie 10

Wypisz wszystkie dzielniki liczby

$4$
$15$
$9$
$21$
$25$
$49$

$1, 2, 4$
$1, 3, 5, 15$
$1, 3, 9$
$1, 3, 7, 21$
$1, 5, 25$
$1, 7, 49$

Ćwiczenie 11

Wszystkie dzielniki liczby $36$ to liczby

R1QPNKjpKgkzL

$1, 6, 12, 36$
$1, 3, 4, 12, 9, 36$
$1, 2, 3, 4, 6, 9, 12, 18, 36$
$1, 2, 3, 6, 9, 12, 36$

Ćwiczenie 12

Wyznacz liczbę, znając jej wszystkie dzielniki.

$1, 2, 5, 10$
$1, 2, 3, 6, 9, 18$
$1, 2, 4, 13, 26, 52$
$1, 2, 3, 5, 6, 10, 15, 30$

$10$
$18$
$52$
$30$

classicmobile

Ćwiczenie 13

Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

Rtm1UYdf3wXYX

Liczba $1$ jest dzielnikiem każdej liczby.
Każda liczba, różna od zera, jest swoim dzielnikiem.
Liczba $2$ jest dzielnikiem każdej liczby parzystej.
Każda liczba, różna od zera, jest dzielnikiem zera.

static

Ćwiczenie 13

Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

R1FE8FF6XLKBG

Liczba $1$ jest dzielnikiem każdej liczby.
Każda liczba, różna od zera, jest swoim dzielnikiem.
Liczba $2$ jest dzielnikiem każdej liczby parzystej.
Każda liczba, różna od zera, jest dzielnikiem zera.

Ćwiczenie 14

Które z podanych iloczynów są podzielne przez $9$ ? Uzasadnij odpowiedź.

R1JTLqlVw27Sg

$9 ∙ 4 ∙ 25$
$18 ∙ 6 ∙ 4$
$25 ∙ 5 ∙ 4$
$27 ∙ 21 ∙ 7$

Dzielniki - zadania

Ćwiczenie 15

Wypisz

wszystkie dzielniki liczby $15$
wszystkie dzielniki liczby $45$
wszystkie wspólne dzielniki liczb $15$ i $45$
największy wspólny dzielnik liczb $15$ i $45$

dzielniki $15 : 1, 3, 5, 15$
dzielniki $45 : 1, 3, 5, 9, 15, 45$
wspólne dzielniki: $1, 3, 5, 15$
największy wspólny dzielnik $: 15$

Ćwiczenie 16

Wyznacz.

$NWD (12, 3)$
$NWD (8, 10)$
$NWD (5, 10)$
$NWD (6, 18)$
$NWD (10, 15)$
$NWD (18, 27)$

Ćwiczenie 17

Ania ma $18$ cukierków i $12$ ciasteczek. Ilu najwięcej gości może zaprosić, aby każdy z uczestników przyjęcia, łącznie z Anią, otrzymał po tyle samo słodyczy?
$5$ osób

Ćwiczenie 18

Wypisz wszystkie dzielniki liczby $28$ . Dodaj do siebie wszystkie dzielniki, z wyjątkiem największego.
Jaką liczbę otrzymasz?

$28$

Ciekawostka

Liczba $28$ jest liczbą doskonałą.
Liczba jest doskonała, gdy jest równa sumie swoich dzielników właściwych (tj. wszystkich dzielników naturalnych mniejszych od niej samej).

Ćwiczenie 19

Znajdź inną liczbę doskonałą, mniejszą od $10$ .

$6$

Ćwiczenie 20

Poszukaj informacji, ile jest liczb doskonałych mniejszych od $1 000$ ? Jakie to liczby?

Rozwiązywanie zadań tekstowych

Cechy podzielności liczb

Wielokrotności i dzielniki liczb naturalnych

Wielokrotności

Dzielniki

Dzielniki - zadania