Słowniczek
Dla dowolnej liczby zachodzi równość
Na przykład
czyli
Czworościan to ostrosłup trójkątny. Czworościan ma wierzchołki i krawędzi. Jeżeli wszystkie ściany czworościanu są trójkątami równobocznymi, to czworościan nazywamy czworościanem foremnym.
Iloczyn potęg o takich samych podstawach
Dla dowolnej liczby rzeczywistej i dowolnych liczb całkowitych i prawdziwa jest równość
Iloraz potęg o takich samych podstawach
Dla dowolnej liczby rzeczywistej i dowolnych liczb całkowitych i prawdziwa jest równość
Iloczyn potęg o takich samych wykładnikach
Dla dowolnych liczb rzeczywistych i i dowolnej liczby całkowitej prawdziwa jest równość
Iloraz potęg o takich samych wykładnikach
Dla dowolnych liczb rzeczywistych i i dowolnej liczby całkowitej prawdziwa jest równość
Zbiór nazywamy dziedziną funkcji, a jego elementy argumentami funkcji.
Funkcją ze zbioru w zbiór nazywamy przyporządkowanie, w którym każdemu elementowi zbioru przyporządkowany jest dokładnie jeden element zbioru .
Funkcję nazywamy malejącą, jeżeli wraz ze wzrostem argumentów maleją wartości funkcji.
Funkcję nazywamy rosnącą, jeżeli wraz ze wzrostem argumentów rosną wartości funkcji.
Funkcję nazywamy stałą, jeżeli wraz ze wzrostem argumentów wartość funkcji pozostaje stała.
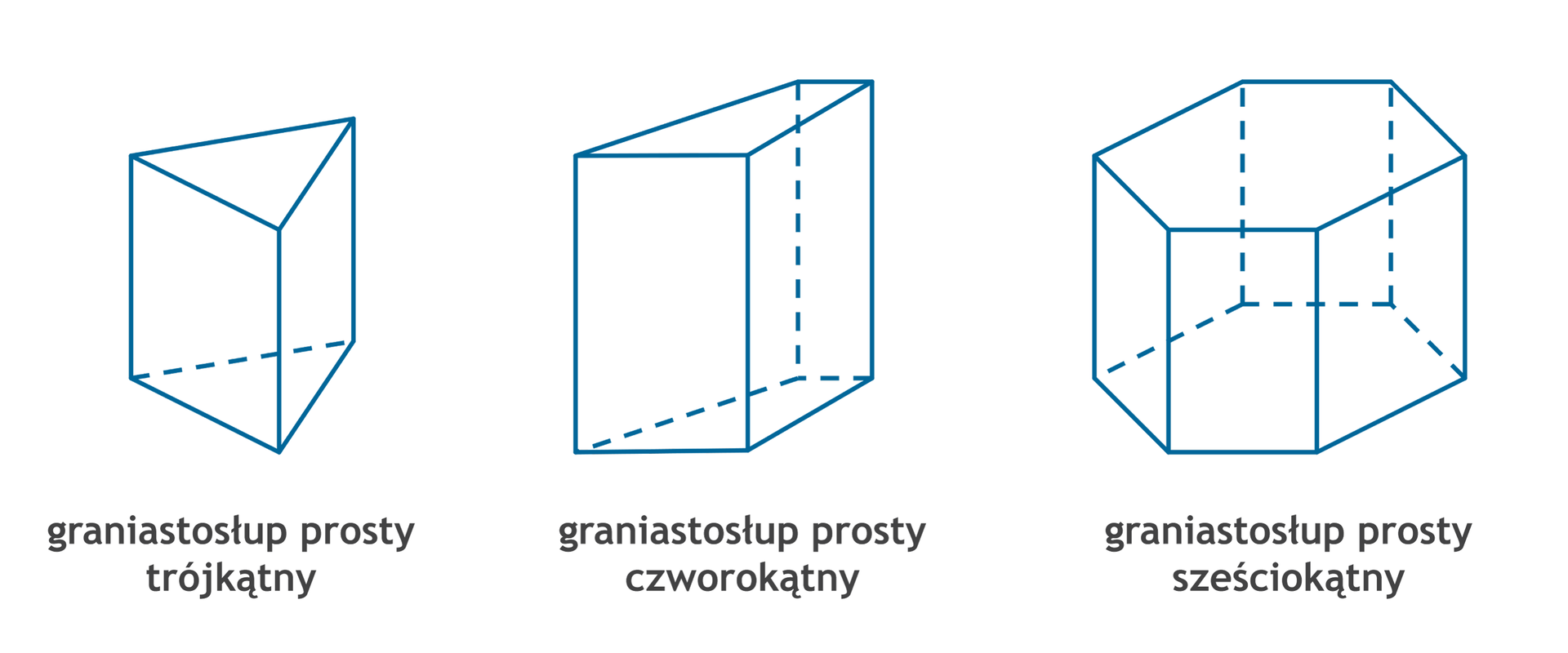
Graniastosłup prosty to taka figura przestrzenna, która ma
dwie podstawy będące jednakowymi wielokątami,
ściany boczne będące prostokątami.
Nazwa graniastosłupa zależy od rodzaju wielokąta w podstawie.
Jednomianem nazywamy wyrażenie algebraiczne, które jest liczbą, literą lub iloczynem liczb i liter.
Miejscem zerowym funkcji nazywamy każdy argument, dla którego funkcja przyjmuje wartość .
Ostrosłup prosty nazywamy prawidłowym, gdy jego podstawą jest wielokąt foremny.
Ściany boczne takiego ostrosłupa są przystającymi trójkątami równoramiennymi.

Ostrosłup nazywamy prostym, gdy jego wszystkie krawędzie boczne są równe. W przeciwnym razie – ostrosłup nazywamy pochyłym. Ściany boczne ostrosłupa prostego są trójkątami równoramiennymi.

Pierwiastkiem kwadratowym z liczby nieujemnej nazywamy taką liczbę nieujemną , której kwadrat jest równy liczbie . Pierwiastek ten oznaczamy symbolem .
Pierwiastek kwadratowy nazywany jest również pierwiastkiem stopnia drugiego.
Mówimy, że liczba w wyrażeniu to liczba podpierwiastkowa.
Pierwiastkiem sześciennym z liczby nazywamy taką liczbę , której sześcian jest równy liczbie . Pierwiastek ten oznaczamy symbolem .
Pierwiastek sześcienny nazywany jest również pierwiastkiem stopnia trzeciego.
wtedy i tylko wtedy, gdy .
Pole sześciokąta foremnego o boku długości jest równe
Sześciokąt foremny, którego bok ma długość , można podzielić na przystających trójkątów równobocznych. Długość boku takiego trójkąta jest równa , zatem jego pole to .
Pole sześciokąta foremnego jest sześciokrotnie większe od pola trójkąta, zatem

Pole trójkąta o wysokości poprowadzonej do podstawy długości jest równe .

Pole trójkąta prostokątnego o przyprostokątnych długości i jest równe

Pole trójkąta równobocznego o boku długości jest równe .

Potęga potęgi
Dla dowolnej liczby i dowolnych liczb całkowitych i prawdziwa jest równość
Zbiór nazywamy przeciwdziedziną funkcji, a każdy element tego zbioru, który został przyporządkowany co najmniej jednemu argumentowi , nazywamy wartością funkcji dla argumentu co zapisujemy symbolicznie
Symbolicznie funkcję określoną w zbiorze o wartościach w zbiorze zapisujemy w postaci
Przekątną prostopadłościanu nazywamy odcinek łączący dwa wierzchołki prostopadłościanu leżące na różnych podstawach i różnych ścianach bocznych.

Niech liczby , gdzie i będą długościami boków trójkąta.
Trójkąt ten jest prostokątny wtedy i tylko wtedy, gdy .
Trójkąt ten jest ostrokątny wtedy i tylko wtedy, gdy
Trójkąt ten jest rozwartokątny wtedy i tylko wtedy, gdy .
Równaniem nazywamy równość dwóch wyrażeń algebraicznych, przy czym przynajmniej w jednym z tych wyrażeń występuje co najmniej jedna zmienna, zwana niewiadomą.
Na przykład:
Jeżeli suma kwadratów długości dwóch boków trójkąta jest równa kwadratowi długości trzeciego boku, to trójkąt ten jest prostokątny.
Jeżeli i są długościami przyprostokątnych, zaś długością przeciwprostokątnej w trójkącie prostokątnym, to zachodzi związek

Wielokąt jest wklęsły, jeżeli co najmniej jeden z jego kątów ma miarę większą od . Wielokąt, który nie jest wklęsły, to wielokąt wypukły.
Jeżeli odcinek łączący dwa dowolne punkty w wielokącie jest całkowicie w nim zawarty, to taki wielokąt nazywamy wypukłym.
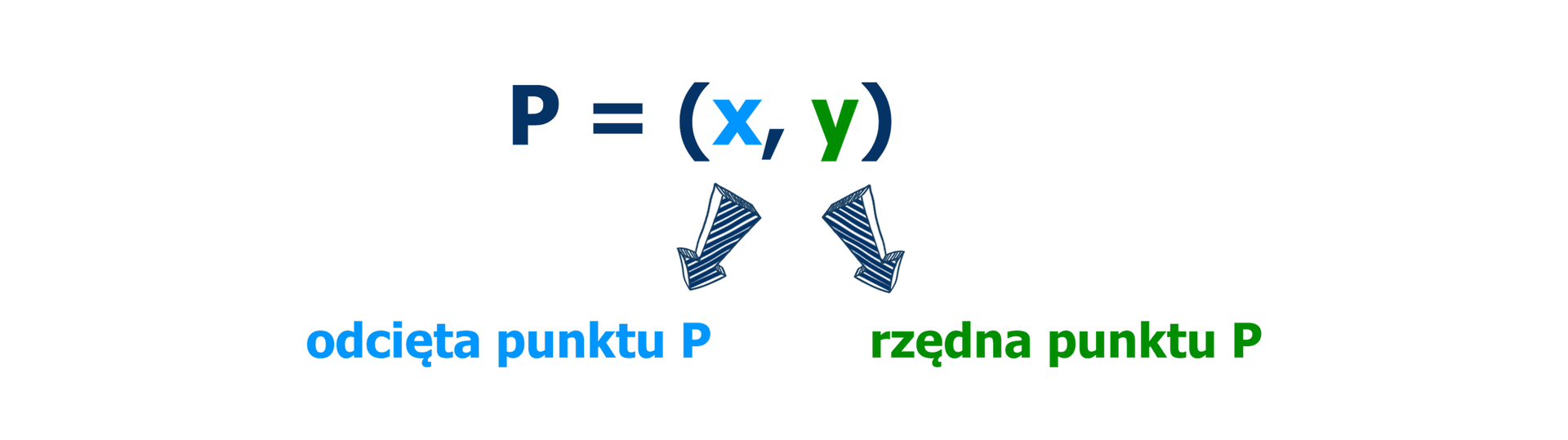
Każdemu punktowi zaznaczonemu w układzie współrzędnych odpowiada uporządkowana para liczb nazywanych jego współrzędnymi.
Zapisujemy
Zbiorem miejsc zerowych nazywamy zbiór wszystkich argumentów, dla których funkcja przyjmuje wartość .
Zbiór złożony ze wszystkich elementów, które są wartościami funkcji dla wszystkich argumentów dziedziny, nazywamy zbiorem wartości funkcji i oznaczamy .




