Polygons in the coordinate system
Wielokąty w układzie współrzędnych
Learning objectives
You will learn to mark polygons in the coordinate system.
Learning effects
You mark polygons in the coordinate system.
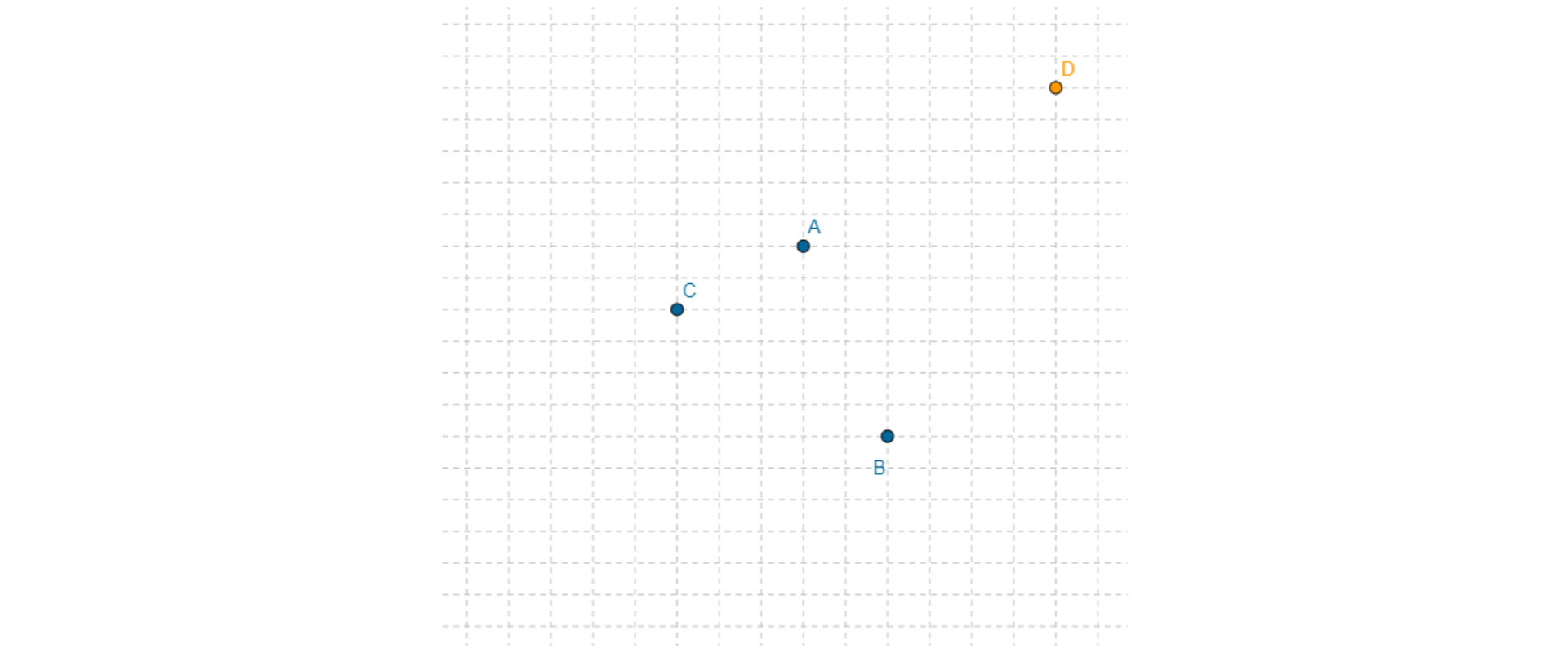
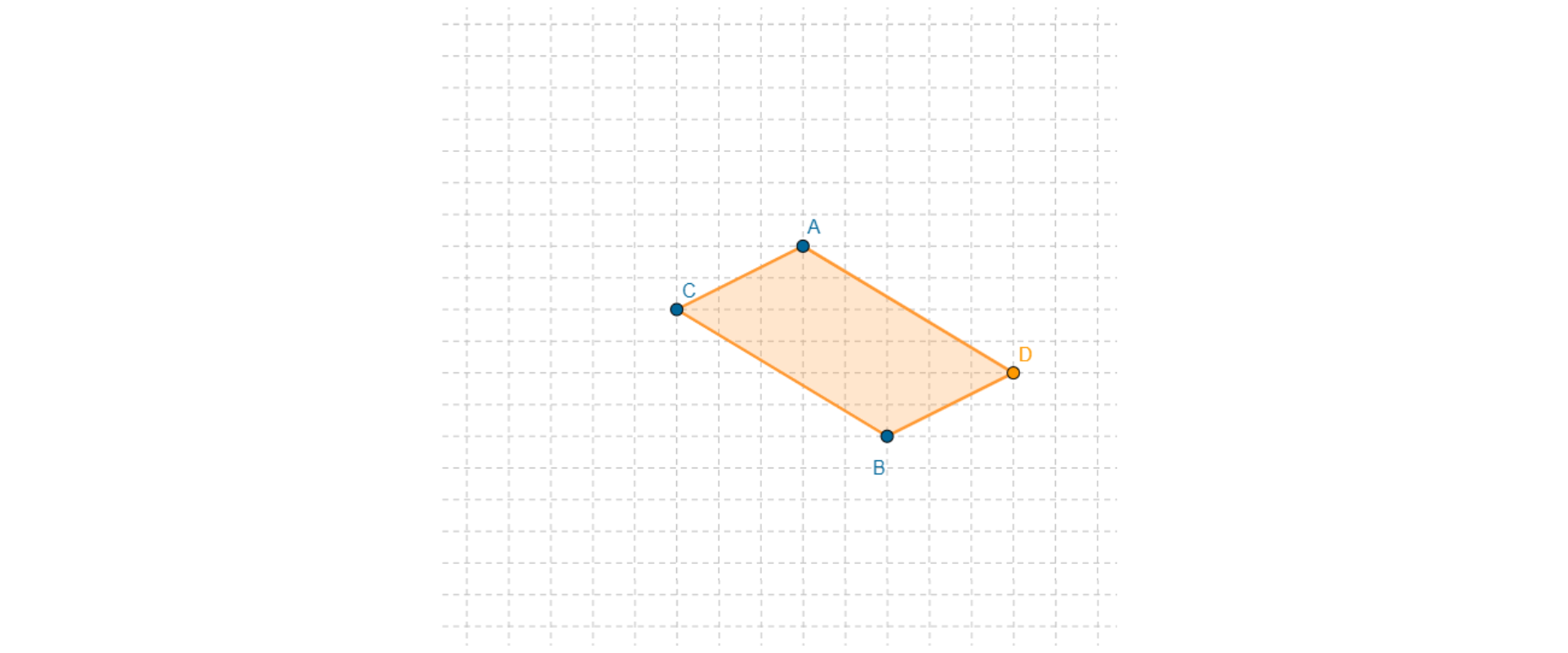
Your task is to mark the fourth vertex in such a way that the obtained tetragontetragon ABCD is a parallelogramparallelogram.
How to calculate lengths of sides of the rectanglerectangle ABCD whose vertices are A (2; 3), B (5; 3), C (5; -2), D (2; -2).
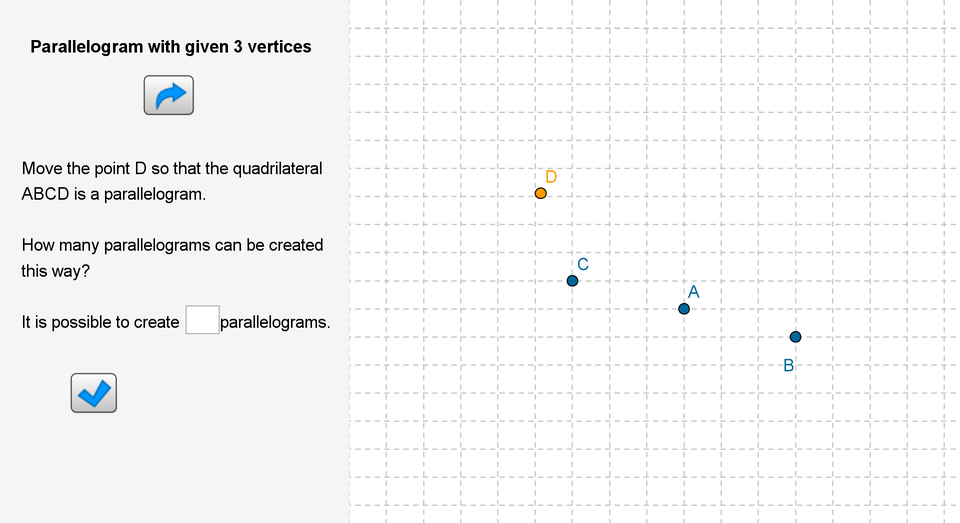
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1H1dSpu8
Mark vertices of a rectanglerectangle in the coordinate systemcoordinate system and try to calculate how many line segment units do sides of the figure have.
Conclusions:
In order to calculate lengths of sides of a polygonpolygon, it is convenient to place it in such a way in the coordinate systemcoordinate system that its vertices are on points of integer coordinates.
If the side AB of a polygonpolygon is parallel to the X axis of the coordinate systemcoordinate system, the length of the side is equal to the absolute value of the difference of first coordinates of points A and B.
If the side CD of a polygonpolygon is parallel to the Y axis of the coordinate systemcoordinate system, the length of the side is equal to the absolute value of the difference of second coordinates of points C and D.
Use obtained information in exercises.
There are points in the coordinate system A (-1; 0), B (5; 0), C (3; 2).
Find such point D that the polygonpolygon ABCD is an isosceles trapezoidisosceles trapezoid. Calculate lengths of bases of this trapezoid.
There is the parallelogramparallelogram ABCD in the coordinate systemcoordinate system.
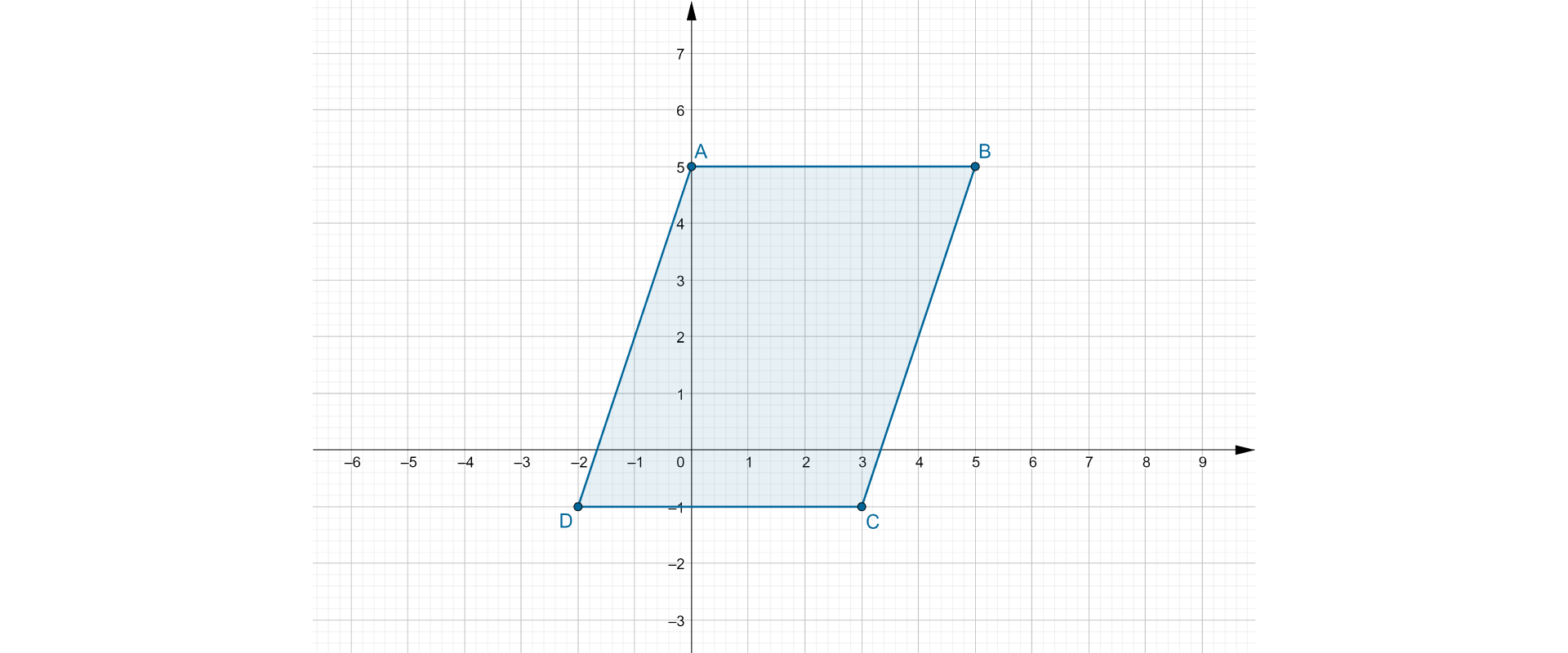
a) Are abscissas of points C and D the same?
b) How many points with both positive coordinates are inside the parallelogramparallelogram ABCD?
c) Give the difference between the ordinate and the abscissa of the point B.
d) Calculate the length of the shorter side of the parallelogramparallelogram ABCD.
There are points A (3; 2) and B (-3; 2).
Find such points C and D that the centre of symmetry of the rectanglerectangle ABCD is the beginning of the coordinate systemcoordinate system. Calculate lengths of sides of this rectanglerectangle.
Mark points in the coordinate systemcoordinate system A (-1; -1), B ( 2; 2), C (0; 4).
Give coordinates of such point D that the obtained tetragon is:
a) a rectanglerectangle that is not a square,
b) a square,
c) a right‑angled trapezoid that is not a rectanglerectangle,
d) a deltoiddeltoid.
Is there a solution for each case?
An extra task:
Calculate the length of the longest side of the ABC triangletriangle whose vertices are A (-3; -1), B (2; -1), C (2; 4).
Do the revision exercises.
Exercises
Mark points A(2; -1), B(4; 1), C(-1; 2) in the coordinate system and connect them one by one. The figure you will obtain is:
- a right-angled triangle
- an acute triangle
- an isosceles triangle
- an obtuse triangle
There is the ABC triangle whose vertices are A (1; 2), B (3; 5), C (-1; 2). Which of the points is located inside the ABC triangle?
G (4; 1)
H (2; 1)
I (3; 5)
J (-1; 3)
Mark the isosceles trapezoid ABCD in the coordinate system. Its longer base AB’s length is 8 and shorter CD is 4. Mark it in such a way that the Y axis is the axis of symmetry of this trapezoid. Describe the solution in English.
Indicate which pairs of expressions or words are translated correctly.
- wielokąt - polygon
- trójkąt - triangle
- czworokąt - tetragon
- układ współrzędnych - coordinate system
- czworokąt - triangle
- deltoid - rectangle
- rectangle
- tetragon
- czworokąt
- prostokąt
- deltoid
- deltoid
- parallelogram
- polygon
- równoległobok
- wielokąt
Glossary
układ współrzędnych
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: coordinate system
deltoid – czworokąt mający oś symetrii, która przechodzi przez dwa jego wierzchołki
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: deltoid
trapez równoramienny
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: isosceles trapezoid
równoległobok
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: parallelogram
wielokąt
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: polygon
prostokąt
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: rectangle
czworokąt – wielokąt o czterech bokach
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: tetragon
trójkąt
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: triangle
Keywords
deltoiddeltoid – a tetragon whose axis of symmetry goes through two its vertices
parallelogramparallelogram
polygonpolygon
rectanglerectangle
tetragontetragon – a polygon with four sides