Kąty i ich rodzaje
Film dostępny na portalu epodreczniki.pl
Animacja
Dwie półproste o wspólnym początku rozcinają płaszczyznę na dwie części. Każdą z tych części, wraz z tymi półprostymi nazywamy kątem.
Wierzchołkiem kąta nazywamy wspólny początek obu półprostych, a każdą z półprostych nazywamy ramieniem kąta.
Półproste i wyznaczają dwa kąty. Każdy z nich możemy oznaczyć symbolem . Aby wskazać o który kąt chodzi, zaznaczamy go odpowiednim łukiem.
Rodzaje kątów
Film dostępny na portalu epodreczniki.pl
Animacja
Jeśli ramiona kąta uzupełniają się do prostej, to taki kąt nazywamy półpełnym.
R1Lrhp5b8rekq1 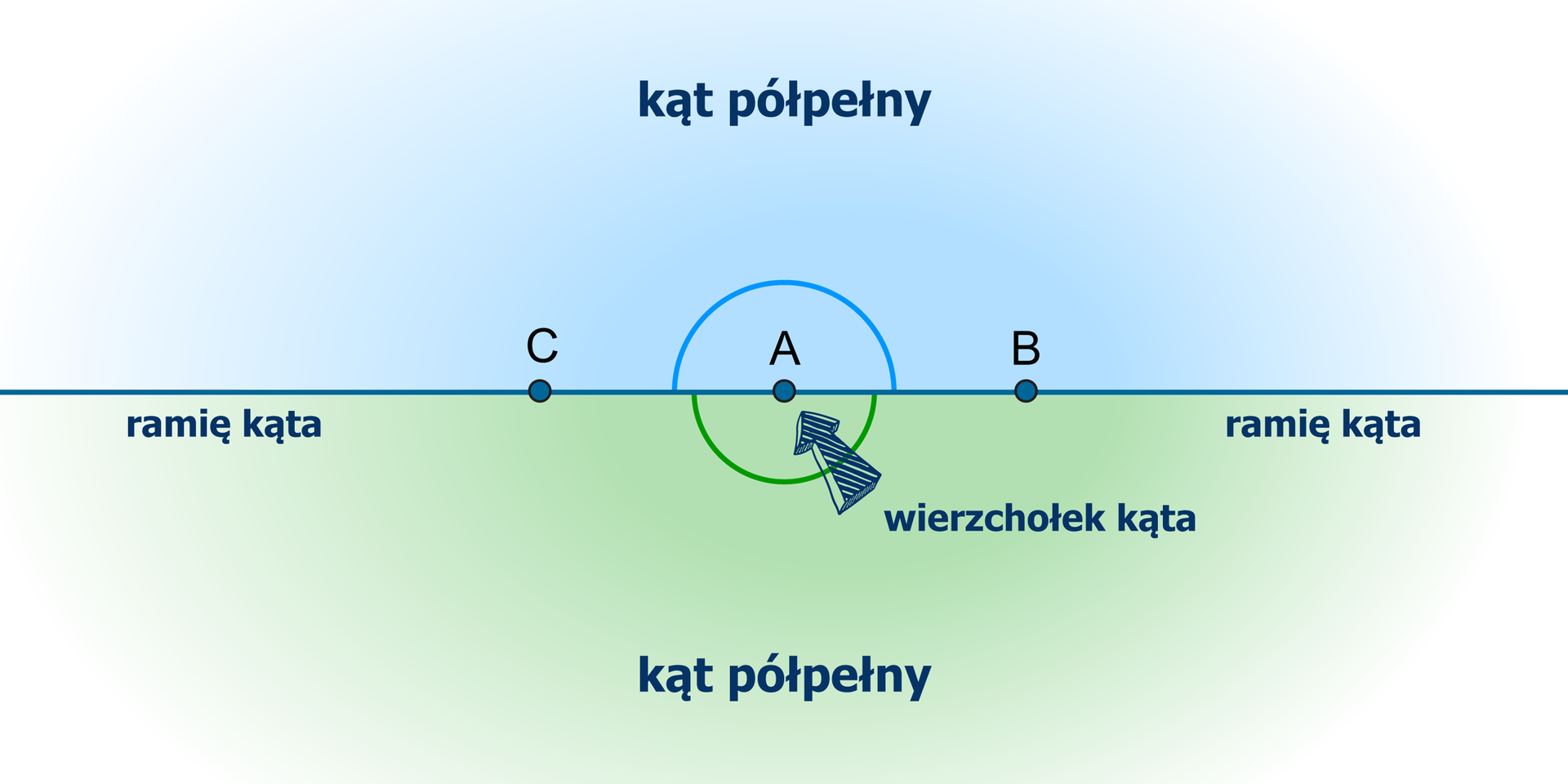 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Gdy ramiona kąta pokrywają się, wyznaczają kąt pełny lub kąt zerowy.
RAUq690TXT69N1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Najczęściej używaną jednostką miary kąta jest stopień.
Jeden stopień to minut kątowych Jedna minuta to sekund
Kąty mające tę samą miarę nazywać będziemy kątami równymi lub przystającymi.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DUMe8Id18
Kąt, którego miara jest mniejsza od , ale większa od , nazywamy kątem ostrym.
Kąt, którego miara jest równa , nazywamy kątem prostym.
Kąt, którego miara jest większa od , ale mniejsza od , nazywamy kątem rozwartym.
RMy9sLyDS4AHh1 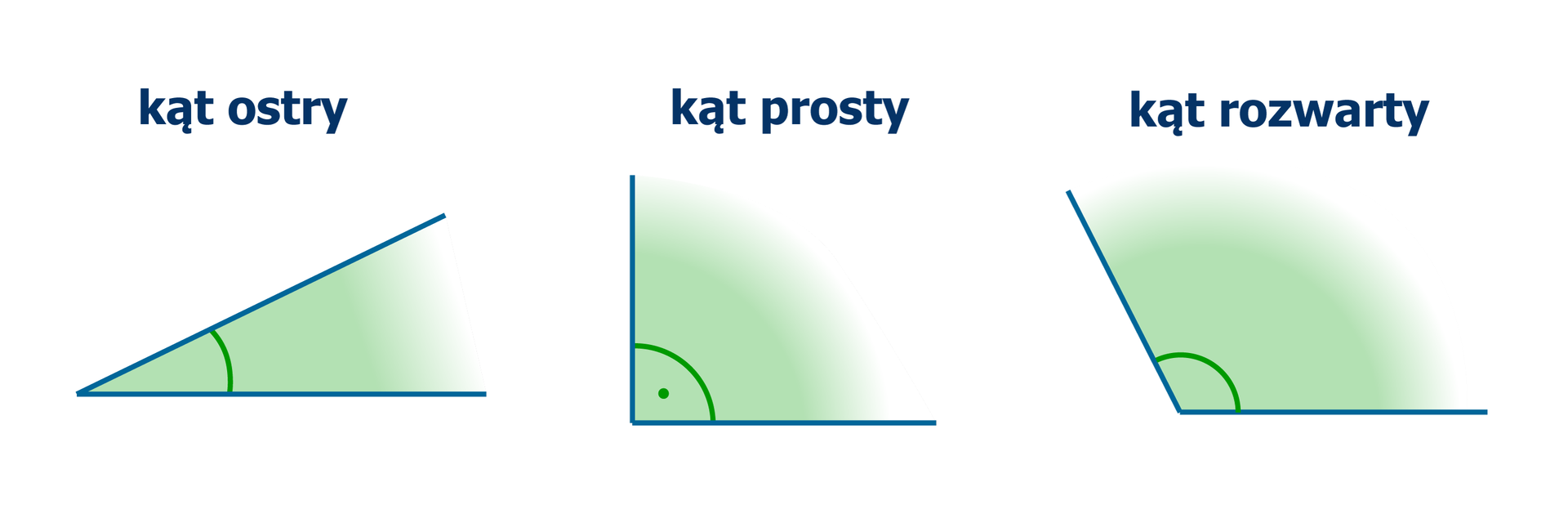 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Kąty, których miara jest mniejsza od lub równa nazywamy kątami wypukłymi.
Kąty, których miara jest większa od , ale mniejsza od , to kąty wklęsłe.
RHzS3D7shCIkp1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
W naukach przyrodniczych najczęściej wykorzystywaną miarą kąta jest miara łukowa. Jednostką jest radian. Miary kątów pojawiają się w wielu wzorach fizycznych. Kąty wyrażone w radianach dają prostsze wyniki niż miary wyrażone w stopniach. Jednakże mierzenie kątów w stopniach w życiu codziennym jest tak popularne, że matematycy i przyrodnicy nie rezygnują całkowicie ze stosowania miary stopniowej.
Kąty wierzchołkowe i przyległe

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DUMe8Id18

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DUMe8Id18
Kąty przyległe to dwa kąty wypukłe, które mają jedno ramię wspólne, a pozostałe ramiona dopełniają się do prostej.
Kąty wierzchołkowe to dwa kąty wypukłe, które mają wspólny wierzchołek i przedłużeniem ramion jednego kąta są odpowiednie ramiona drugiego kąta.
R17EFmv3QSulO1 Na przykład i na rysunku są kątami przyległymi. Pary kątów wierzchołkowych to i oraz i

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DUMe8Id18
Suma miar kątów przyległych jest równa .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DUMe8Id18
Dowód
Wprost z twierdzenia o sumie miar kątów przyległych wynika, że
oraz
Stąd . Wynika stąd, że kąty wierzchołkowe są równe.
Kąty wierzchołkowe mają równe miary.
Obliczmy miary kątów i zaznaczonych na rysunku.

Kąty o miarach i to kąty wierzchołkowe, więc Każdy z kątów i jest przyległy do kąta o mierze Zatem
Wyznaczymy miary kątów równoległoboku

Kąty i to kąty wierzchołkowe, mają więc równe miary.
Suma kątów równoległoboku leżących przy jednym boku jest równa 180.
Kąty i leżą przy jednym boku.
W równoległoboku kąty leżące naprzeciw siebie mają równe miary.
Kąt leży naprzeciw kąta , kąty te mają więc równe miary.
Podobnie kąt leży naprzeciw kąta , kąty te mają równe miary.
Odpowiedź: Miary kątów równoległoboku są równe:
Określ rodzaj kąta.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DUMe8Id18
Porównywanie kątów.
Film dostępny na portalu epodreczniki.pl
Animacja
Narysuj dwa różne kąty i porównaj je.
Uzupełnij zdania, korzystając z rysunku.

jest kątem przyległym do kąta … lub do kąta ….
Kąt … i kąt to kąty wierzchołkowe.
Suma miary kąta i miary kąta … lub miary kąta … jest równa .
Uzupełnij zdania.
Jeśli dwa kąty przyległe są równe, to miara każdego z nich jest równa …
Suma kątów … jest równa kątowi półpełnemu.
Z dwóch kątów przyległych jeden jest o większy od drugiego. Kąty te mają miary
- i
- i
- i
- i
Jeden z kątów przyległych ma miarę osiem razy większą od drugiego. Oblicz miary tych kątów.
Narysuj dowolny kąt Ile kątów przyległych do kąta możesz narysować?
Narysuj romb. Podaj miary kątów wierzchołkowych oraz przyległych, jakie tworzą przekątne w rombie.
Oblicz miary kątów

Oblicz miarę kąta

Określ rodzaj kąta.

kąt ostry …
kąt prosty …
kąt rozwarty …
kąt półpełny …
kąt pełny …
kąt wklęsły …
kąt wypukły …
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Kąt półpełny jest kątem ostrym.
- Kąty przyległe mają równe miary.
- Kąty wierzchołkowe mają równe miary.
- Kąt prosty jest kątem wypukłym.
Przesuwając punkt , ustaw ramię kąta tak, aby miara tego kąta była równa podanej wartości. Skorzystaj z kątomierza.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DUMe8Id18
