Points, lines and planes in space – doing exercises
Punkty, proste i płaszczyzny w przestrzeni – rozwiązywanie zadań
Learning objectives
You will learn to draw lines in space (according to conditions of the task).
You will learn to apply the concept of an angle between the line and the plane as well as the dihedral angle between half‑planes.
Learning effect
You draw lines in space (according to conditions of the task) and to apply the concept of an angle between the line and the plane as well as the dihedral angle between half‑planes.
Open the slideshow and observe drawings that illustrates relations between lines and planes in space.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DV1IqYUbx
Do tasks that are divided into four thematical areas.
Area I - Mutual position of a line and a plane.
There is a parallelogram ABCD whose diagonals cross at point P and the point S that does not belong to the plane ABCD. Moreover, we know that line segments AS and SC as well as SD and SB are respectively equal to each other. Define the location of the line segment PS with respect to the plane ABCD. Justify the answer.
Area II - Mutual position of lines in space.
Draw a cube ABCDEFGH. Fill in the table by writing four examples of proper lines, determined by vertices of this cube.
parallel lines | crossing lines | oblique lines |
Area III - Angles between a line and a plane
There is a line segment AB located on the plane p and a point C located in a distance equal to the length of the line segment AB. Find the angle between the line AC and the plane p if the midpoint of the line segment AB is an orthographic projection of the point C on the plane p.
Area IV - The dihedral angledihedral angle between two half‑planes.
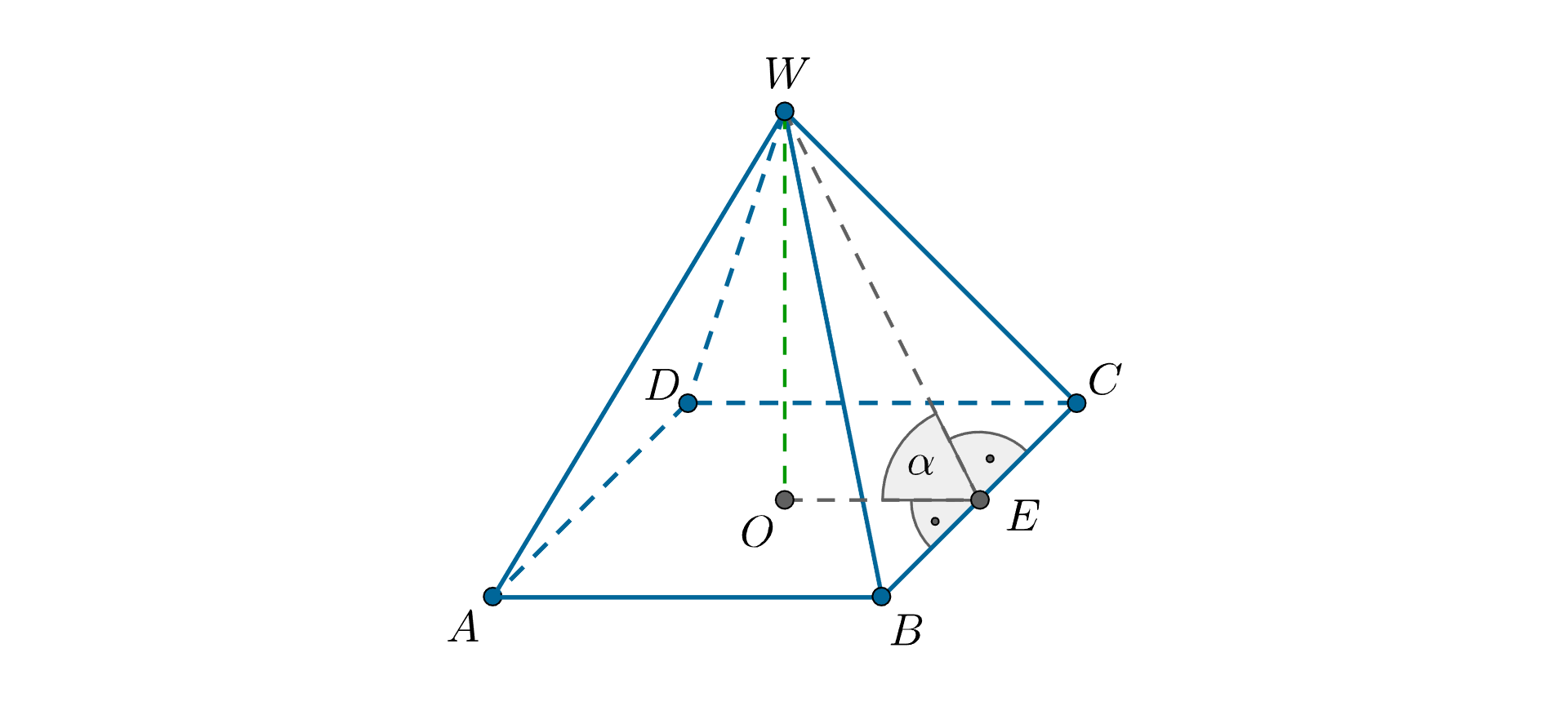
Identify the angle of inclination of the side wall to the plane of the base in the drawn pyramid, knowing that all its edges have the same length.
An extra task:
The line segment whose length is a is inclined to the plane p at the angle 60°. Calculate the length of the orthographic projection of this line segment on the plane p.
Remember
A line can be located on the plane, break the plane or have no common points with the plane.
Two lines in space can overlap, be located on one plane or not be located on one plane and have no common points (be oblique).
The line k and the plane p are perpendicular only and only if the line k is parallel to each line located on the plane p,
The angle between the line k and the plane p is the acute angle between this line and orthographic projection on the plane p,
If the line l breaks the plane p and is not perpendicular to it, the line k is an orthographic projection of the line l on the plane p, the line m is located on the plane p and crosses the line l, then the line m is perpendicular to the line l only and only if it is perpendicular to the line k (theorem about three perpendicular lines).
The dihedral angledihedral angle is the sum of two half‑planes with common edge and one of two areas that this half‑planes cut from the space,
The linear anglelinear angle of the dihedral angledihedral angle is the common part of the dihedral angledihedral angle and the plane perpendicular to its edge.
Exercises
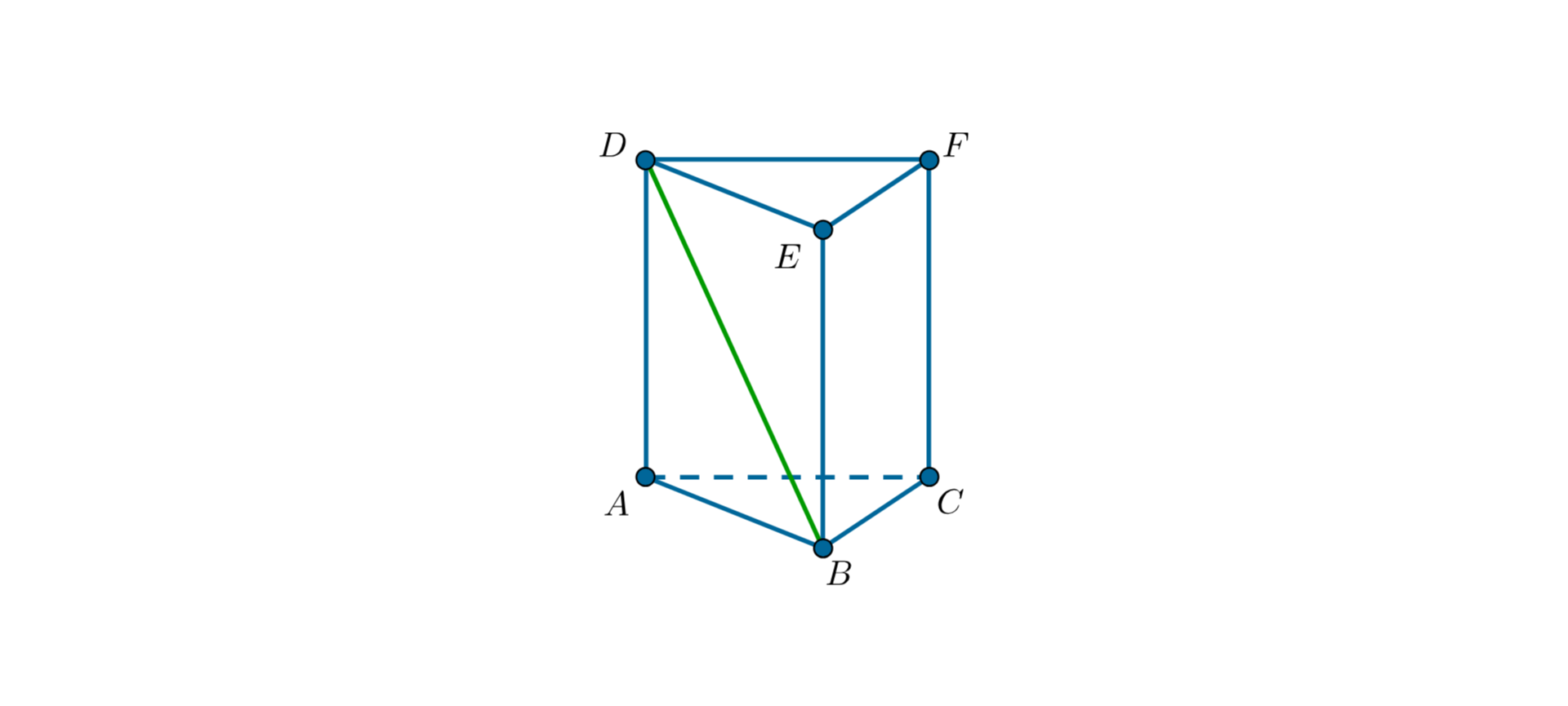
In the prism in the picture there are lines DB and AC. Those lines:
- have one common point
- are parallel
- are perpendicular
- are oblique
Point a is located inside the dihedral angle. Distance between this point and each wall of this angle is 10 cm and the angle between this distances is 120°. Calculate the distance between the point A and the edge of the dihedral angle.
On the plane p, there are two parallel line a and b whose distance from each other is 20 cm. There is a line c, parallel to lines a and b, located outside of this plane. The distance from the line c to the plane p is 12 cm and the distance between the line c and the line b is 13 cm.
Calculate the length between the line c and the line a. Make a proper drawing. Describe the drawing and write the answer in English.
Indicate which pairs of expressions or words are translated correctly.
- położenie prostej i płaszczyzny - location of a line and a plane
- położenie dwóch prostych w przestrzeni - location of two lines in space
- kąt nachylenia prostej do płaszczyzny - angle between the line and the plane
- kąt dwuścienny - dihedral angle
- prosta prostopadła do płaszczyzny - line breaking the plane
- kąt dwuścienny - linear angle
- położenie prostej i płaszczyzny
- kąt nachylenia prostej k do płaszczyzny p
- kąt dwuścienny
- położenie dwóch prostych w przestrzeni
- the dihedral angle
- the linear angle
- kąt liniowy
- the angle between the line k and the plane p
- location of a line and a plane
- location of two lines in space
Glossary
kąt nachylenia prostej do płaszczyzny
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: angle between the line and the plane
kąt dwuścienny
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: dihedral angle
prosta przebijająca płaszczyznę
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: line breaking the plane
prosta prostopadła do płaszczyzny
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: line perpendicular to the plane
kąt liniowy
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: linear angle
położenie prostej i płaszczyzny - prosta może leżeć na płaszczyźnie, przebijać ją lub nie mieć z nią punktów wspólnych.
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: location of a line and a plane
położenie dwóch prostych w przestrzeni- dwie proste w przestrzeni mogą się pokrywać, leżeć w jednej płaszczyźnie lub nie leżeć w jednej płaszczyźnie i nie mieć punktów wspólnych (są skośne).
Nagranie dostępne na portalu epodreczniki.pl
wymowa w języku angielskim: location of two lines in space
Keywords
angle between the line k and the plane pangle between the line k and the plane p,
dihedral angledihedral angle,
linear anglelinear angle,
location of a line and a planelocation of a line and a plane,
location of two lines in spacelocation of two lines in space